Reliability Estimation of Aviation Pyrotechnics System Based on Mixed Beta Distribution
LAI Yue-hua (赖岳华), DONG Hai-ping (董海平)*, CHENG Tao (程 涛), YANG Shu-bin (杨树彬)
1 School of Mechatronical Engineering, Beijing Institute of Technology, Beijing 100081, China 2 The 213th Research Institute of China Ordnance Industry, Xi’an 710061, China
Reliability Estimation of Aviation Pyrotechnics System Based on Mixed Beta Distribution
LAI Yue-hua (赖岳华)1, DONG Hai-ping (董海平)1*, CHENG Tao (程 涛)2, YANG Shu-bin (杨树彬)2
1SchoolofMechatronicalEngineering,BeijingInstituteofTechnology,Beijing100081,China2The213thResearchInstituteofChinaOrdnanceIndustry,Xi’an710061,China
For evaluating reliability of an aviation pyrotechnics system, a Bayesian reliability estimation method utilizing reliability information of a system and its units was put forward. Firstly, an inheritance factor was determined by chi-square goodness of fit test. Then the mixed prior distribution was obtained based on the inheritance factor. Finally, the density function of posterior distribution was obtained and used to assess the reliability of system. According to the new method, the reliability of an aviation pyrotechnics system was evaluated to reach 0.989 6 at the confidence level of 0.90. To reach the reliability index, the required numbers of trials of system and its units were given. It is instructional to apply the new method on the reliability estimation of aviation pyrotechnics systems.
aviationpyrotechnicssystem;reliability;mixedBetadistribution;inheritancefactor;posteriordistribution
Introduction
This aviation pyrotechnics device is a kind of one-shot products. It is used to cut the glass of helicopter cockpit for separating glass from helicopter in emergency. It can clean channel for pilots to survive. At the same time, it is not allowed to hurt the crew’s body. The device is very important to save pilots’ lives. Therefore, it has high requirements on reliability. Usually, in the final design period, its reliability should reach 0.99 at the confidence level of 0.90 based on trials’ results. Because the trials are destructive, limited by cost and other factors, the number of trials of system in the final design period is small. Generally, the number of trials of system will not be beyond about 30 times. If we apply the binomial distribution to make the confidence interval estimation for its success probability, we can obtain the lower confidence limit of reliability is 0.926 at the confidence level of 0.90. Nevertheless, it can’t meet the requirements on reliability, and the design in the final period may be delayed.
In fact, due to the high cost of trials of system, a lot of trials about each unit will be done in the development process generally. It is an effective method that combines these trials with a small amount of trials of system comprehensively to ensure the high reliability of system. This method can not only guarantee the high reliability, but also can reduce the cost of trials. The classical statistical method aforementioned based on the binomial distribution ignores the trial information of units. It can’t accurately reflect the real level of reliability of system in the estimation results if we only use the data of trials of system. The most important thing is that how to utilize the data of trials of the aviation pyrotechnics system and its units to conduct reliability estimation. To solve this similar problem, many researchers in our country or abroad adopted Bayesian theory to utilize all kinds of data while conducting the reliability assessment of complex systems[1-8]. However, these methods used in different systems were not effective for identifying whether or not all kinds of data were the same population. For this problem, Wangetal. presented a Bayesian method based on mixed Beta distribution to assess reliability of such systems[9]. Dongetal. applied the Bayesian method based on mixed Beta distribution to assessing the reliability of rocket ejection seat through combining test data of whole seat and its subsystems, and the result showed that this method was feasible[10]. So, in this paper, a Bayesian reliability estimation method based on mixed Beta distribution for assessing the reliability of aviation pyrotechnics system is put forward, and the required numbers of trials of system and its units to reach the requirements of reliability are also given.
1 Bayesian Method for Reliability Estimation
1.1 Determination of the mixed prior distribution
As to the reliability estimation method based on Bayesian theory, we should collect the information of reliability before the beginning of trials of system. Taking these previous information as prior information of reliability of system and combining the prior information with the data of field trials of system, we can obtain a comprehensive estimation about the reliability of system[11].
The key of Bayesian method lies in using prior information to determine a prior distribution. As to the trials whose result is either success or failure, that is, its distribution is binomial distribution, the prior distribution of its population is usually assumed to be the conjugative distribution of binomial distribution —Beta(R|a,b) on engineering applications. The density function of prior distribution is shown in Eq. (1):
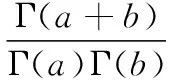
(1)
where 0 Assumenis the number of trials of system,sis the number of success, andfis the number of failure. The prior distribution is ready, and if the data of trials of system (n,s) is obtained, the posterior distribution of binomial distribution —Beta(R|a+s,b+f) can be obtained easily. Its density function is shown in Eq. (2): (2) (3) Taking Eq. (1) as the density function of prior distribution, the posterior expectation of reliabilityRcan be estimated in Eq. (4)[12]: (4) whereq=n/(a+b+n),s/nis the mean value of samples, anda/(a+b) is the mean value of prior distribution. According to Eq. (4), the posterior expectation estimation of reliabilityRis the weighted average based on the mean value of samples and the mean value of prior distribution, and the proportion is decided by the super parametersa,band the number of samplen. Assuming that the data of trials of system and the virtual equivalent data of system come from two different populationsXandY, in order to minimize the impact which is caused by the assumption and the influence act on reliability estimation, as well as, make full use of the virtual equivalent data of system, the mixed prior distribution is presented. For the population that follows binomial distribution, the density function of mixed prior distribution[3]is shown in Eq. (5): πρ(R)=ρπ(R)+(1-ρ), (5) whereρis called inheritance factor, and 0≤ρ≤1, and (1-ρ) is called update factor. Ifρ=1, it represents that the two populations are identical. Ifρ=0, the two populations are different thoroughly. Certainly, if 0<ρ<1, it is between the above two situations. Consequently, the using of density function of mixed prior distributionπρ(R) is a compromise between classical statistical method and traditional Bayesian method. It considers all the circumstances and can be applied into wider domain. Naturally, it is more reasonable than theBeta(R|a,b) distribution. The density function of mixed prior distribution is shown in Eq. (5), and if the data of system trials (n,s) is also got, the density function of posterior distribution can be deduced in Eq. (6): πρ(R|n,s)= (6) where As shown in Eq. (6), the density function of posterior distributionπρ(R|n,s) is also the weighted sum of the two posterior densities. (7) 1.2 Processing of zero-failure data For the systems of high reliability, the data of trials of system are often zero-failure. If there are not performance data obtained by measuring, the virtual equivalent trials of system are also prone to zero-failure. Meanwhile, because the value ofMin Eq. (6) is infinity when applying Eq. (6) to deriving the posterior distribution, it is difficult to use the mixed prior distribution. As the reliability of aviation pyrotechnics system is high relatively, both the trial data of system and its units may be zero-failure. Therefore, a solution for this problem is proposed. (8) (9) According to Eqs. (8) - (9), the result can be obtained as follows: (10) An aviation pyrotechnics system consists of a handle of jettison, mechanical initiator, assemblies of exploder, assemblies of adapter, linear cutting cord, and other components. The handle of jettison is connected with the mechanical detonator. When the mechanical detonator is initiated by the handle, the exploision waves which pass through a small detonator, detonation cord, a small fire cap, and a flame detonator, will ignite the cutting cord. The glass door of the helicopter cockpit will be cut out by the cutting cord. After analyzing the work principle and the process of function realization about the device, the simplified block diagram of the reliability of the aviation pyrotechnics system is shown in Fig.1. Fig.1 Block diagram of an aviation pyrotechnics system In the development process of an aviation pyrotechnics system, the trials of small detonator have been accumulated up to 5450 and all trials succeed. The detonation cord has been tested 3214 times, and each time is successful. The fire cap has been tested 4 080 times, which all succeed. In addition, the number of trial of cutting cord is 196, and the number of failure is zero. Although there aren’t a lot of trials conducted on other units, sensitivity tests or margin tests are carried out so that the lower limit of reliability can be inferred. In accordance with the relationship between reliability and test number, it is reasonable to convert the lower limit of reliability into the data of “virtual” test. The numbers of test sample population of impact detonators and flame detonators are both 2302584 if the margin tests are all successful; and the number of test sample of handle of jettison is 23025 when they are all tested successfully. The trials data of units in this system are all zero-failure, and the equivalent data have the following theorem[13]. This theorem shows that when the aero-failure data are converted into equivalent data, it is a conservative treatment to take the smallest number of trials sample among units as the equivalent trial number of system. From the trial data of each unit in system, the trial number of cutting cord is the smallest. According to Theorem 1, the “virtual” equivalent trial data of aviation pyrotechnics system are (196, 196). In development phase of device, because 26 sets have been tested and none of them fails, the trial data of system (n,s) are (26, 26). If only using trial data of system, making estimation based on the classical statistical methods of binomial distribution, its lower limit of reliability is 0.9152 with confidence level of 0.90. It is far below the reliability requirements in the final design phase. If increasing the trial numbers of cutting cord and system, according to this method of estimation, the results of evaluation are shown in Table 1. Table 1 Lower limit of reliability with different numbers of virtual equivalent trials of system and trials of system As to this aviation pyrotechnics system, from Table 1, if keeping the same number of trials of system and adding 14 trials of cutting cord, or keeping the number of trials of cutting cord unchanged and adding 4 trials of system, the number of virtual equivalent trials of system will be up to 210. Furthermore, the lower limit of reliability of system will reach 0.99, which meets the requirements. If only using the data of trials of system rather than the data of trials of units, at least 204 trials of system need to be added to meet the requirements of reliability. Obviously, utilizing the data of trials of units and the data of trials of system synthetically based on the proposed method to do reliability estimation, which can greatly decrease the number of trials of system and significantly reduce the cost of trials and development cycle. In Table 1, the inheritance factor increases with the increasing of virtual equivalent trials of system while maintaining the number of trials of system constant. If keeping the same number of virtual equivalent trials, the inheritance factor will increase with the increasing of trials of system. This is the nature of inheritance factor. In case of zero-failure data, the closer the numbers of two kinds of trials, the higher the degree of similarity between their reliability, and the inheritance factor should take a larger value; conversely, the greater the difference between the numbers of trials, the lower the degree of similarity between their reliability, and the inheritance factor should take a smaller value. According to the data of trials of the aviation pyrotechnics system and its units, using the reliability estimation method of Bayesian, we can infer that the lower limit of reliability of aviation pyrotechnics system has reached 0.989 6. Now, it has approached to the requirements of reliability of system. In order to make the reliability of system reach the prescribed level of verification, in accordance with the proposed method, the required numbers of trials is offered. It can also provide guidance for future. The proposed method takes account of the situation that virtual equivalent data of system and the field trials data of system may come from different populations. Furthermore, the introduction of inheritance factor makes rational use of the historical information, as well as reduces the number of trials of system. However, this method is more complex on computation than the classical method and Bayesian method whose prior distribution is Beta distribution. In addition, such mixed Beta prior distribution which depends on the degree of similarity between prior information and the data of field trials makes the relationship between prior information and the result of estimation not straight forward. [1] Anderson-Cook C M, Graves T, Hengartner N,etal. Reliability Modeling Using Both System Test and Quality Assurance Data [J].MilitaryOperationsResearch, 2008, 13(3): 5-18. [2] Peng W W, Huang H Z, Xie M,etal. A Bayesian Approach for System Reliability Analysis with Multilevel Pass-Fail Lifetime and Degradation Data Sets [J].IEEETransactionsonReliability, 2013, 62(3): 689-698. [3] Reese C S, Wilson A G, Guo J Q,etal. A Bayesian Model for Integrating Multiple Sources of Lifetime Information in System-Reliability Assessments [J].JournalofQualityTechnology, 2011, 43(2): 127-140. [4] Kleyner A, Bhagath S, Gasparini M,etal. Bayesian Techniques to Reduce the Sample Size in Automotive Electronics Attribute Testing [J].MicroelectronicsReliability, 1997, 37(6): 879-883. [5] Zhang S F. Bayesian Assessment for Product Reliability Using Pass-Out Data [J].ActaArmamentarii, 2001, 22(2): 238-240. (in Chinese) [6] Xiao G. Reliability Assessment of Solid Rocket Engine Based on Converted Information [J].JournalofXi’anJiaotongUniversity, 1999, 33(7): 33-36. (in Chinese) [7] Wilson A G, Graves T L, Hamada, M S,etal. Advances in Data Combination, Analysis and Collection for System Reliability Assessment[J].StatisticalScience, 2006, 21(4): 514-531. [8] Wilson A G, McNamara L A, Wilson G D. Information Integration for Complex Systems [J].ReliabilityEngineering&SystemSafety, 2007, 92(1): 121-130. [9] Wang W, Zhou H Y, Yin G J. Bayesian Method Based on Mixed Beta Distribution [J].SystemsEngineering-Theory&Practice, 2005, 25(9): 142-144. (in Chinese) [10] Dong H P, Cai R J, Wang W. Reliability Assessment of Rocket Ejection Seat Based on Mixed Beta Distribution[J].ActaAeronauticaEtAstronauticaSinica, 2009, 30(2): 232-235. (in Chinese) [11] Tang X M, Zhang J H, Shao F C,etal. Test Analysis and Evaluation of Weapon Systems in Small-Sample Circumstances [M]. Beijing: National Defence Industry Press, 2001: 188-194. (in Chinese) [12] Zhang Y T, Chen H F. Inference of Bayesian Statistics [M]. Beijing: Science Press, 1994. (in Chinese) [13] Zhou Y Q, Reliability Estimation [M]. Beijing: Science Press, 1990. (in Chinese) Foundation item: Advanced Research Fund for National Defense Science and Technology Key Laboratory, China (No.9104C3705021003) 1672-5220(2014)06-0766-04 Received date: 2014-08-08 * Correspondence should be addressed to DONG Hai-ping, E-mail: donghaipingphd@126.com CLC number: TJ450 Document code: A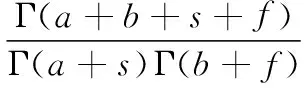

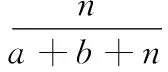
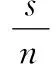

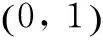
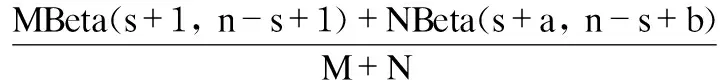

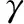
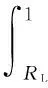
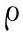
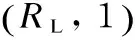
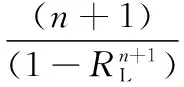
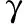
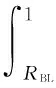
2 Reliability Estimation of an Aviation Pyrotechnic System in a Helicopter



3 Conclusions
 Journal of Donghua University(English Edition)2014年6期
Journal of Donghua University(English Edition)2014年6期
- Journal of Donghua University(English Edition)的其它文章
- Stress-Strength Structural Reliability Model with a Stochastic Strength Aging Deterioration Process
- Settlement Prediction of Dredger Fill with the Optimal Combination Model
- Condition-Based Maintenance Decision-Making for Equipment
- Identification of the Credit Guarantee Network of Steel Trade Enterprises in China
- Methods for Reliability Assessment under Irregular Time-Varying-Stress Degradation Testing
- Efficient Method for Accelerated Reliability Qualification Testing
