现浇盒状内模空心楼盖的直接设计法
黄川腾,王志军
(重庆大学 土木工程学院;山地城镇建设与新技术教育部重点实验室,重庆400045)
空心楼盖由于其结构高度小、自重轻、刚度大、整体性好和适用于大跨度建筑等优点,近年来得到广泛应用。特别地,盒状内模空心楼盖由于其刚度在两跨度方向分布均匀、布模灵活和对异型边板适应性强的优点,较筒体、筒芯内模空心楼盖得到更多青睐,这也激发了许多研究者对盒状内模进行研究,提出了不同材料和形式的盒状内模。虽然这些内模形式略有差异,但其空心楼盖在竖向荷载下力的传递途径和变形方式基本相同[1-4]。
根据国家颁布的现浇空心楼盖技术规程[5],对于规则布置的柱支撑现浇混凝土空心楼盖结构,设计中常采用拟板法、拟梁法、直接设计法和等代框架法,在满足限制条件[5]的情况下采用直接设计法尤为方便快捷。直接设计法包含3个基本步骤:1)确定总的静力弯矩;2)把总静力弯矩分配到负弯矩和正弯矩截面(一次分配);3)把负弯矩和正弯矩分别分配到柱上板带板、柱上板带梁和跨中板带(二次分配)。直接设计法和等代框架法的第3步骤是完全一样的,规程中的直接设计法完全沿用了ACI 318规范中实心楼盖的分配系数。但由于空心的存在,使楼板截面刚度发生了改变,随着空心率的增加,这种刚度的不均匀性越发明显,能否直接使用实心板的分配系数、各截面弯矩分配比例是否有较大变化,国内外学者对这些问题研究较少。周玉等[6]通过有限元数值模拟讨论了实心宽扁梁楼盖在竖向荷载下的弯矩分配系数;Ibrahi m等[7]通过数值模拟讨论了密肋楼盖在开洞和不开洞时直接设计法的弯矩分配系数;袁俊杰[8]结合一个实际工程对筒芯内模空心楼盖进行了拟梁法和直接设计法的算例对比;郭楠等[9]分析了实心板在竖向荷载作用下的弯矩分布规律;刘文珽等[10]对比了中外规范关于实心板柱结构在垂直荷载作用下设计方法的异同,同时对比了直接设计法的弯矩分配系数与有限元计算结果;李海涛等[11-12]分别对一个具体的柱支承筒芯内模现浇钢筋混凝土空心楼盖和对照实心楼盖进行了有限元计算,对直接设计法提出建议。
已有对直接设计法适用性的研究,均未针对盒状内模空心楼盖,并且完成的算例分析数量有限,对空心楼盖各参数的分析也还不完善。结构的弹性内力分析方法可用于正常使用极限状态和承载能力极限状态作用效应的分析,现浇混凝土空心楼盖结构在承载能力极限状态下的内力设计值也是按线弹性分析方法确定的[5],基于这样的原因,本文所有算例与已有研究一样采用弹性分析。针对上述情况,本文利用大型有限元分析软件ABAQUS,在完成分析模型的精度校核后,编制了pyt hon脚本程序[13],进行了224个算例的自动建模及弹性分析,考察了具有相同参数的实心楼盖和空心楼盖的截面弯矩分布的异同,进而分析了空心率(ρ)、板格边比(l2/l1)、柱跨比 (c/l)、梁板相对抗弯刚度比(μ1=和边梁抗扭刚度比(βt=等5个因数对空心楼盖弯矩分布的影响,得到了内板格和端板格各弯矩控制截面的一次弯矩分配系数以及各控制截面内柱上板带板、跨中板带和柱上板带梁的二次弯矩分配系数,并与规范建议的直接设计法系数做了对比,给出了相关建议。
1 楼盖参数及模型验证
通过确定以下几何参数即可确定空心楼盖的布置:计算跨度(l1、l2,下标1表示计算方向,2表示从属方向,下同)、柱子宽度(wc1、wc2)、内梁宽度(wib1、wib2)、内 梁 高 度 (hib1、hib2)、边 梁 宽 度(web1、web2)、边梁高度(heb1、heb2)、实心区域宽度(ws1、ws2)、内模边长(lb)、内模高度(hb)、内模间肋宽(wb1、wb2)和顶底板厚度(ts)。通过各参数的组合,可以得到具有不同空心率的空心楼盖。本文以纵横向均为3跨的空心板-柱结构为例,考虑对称性,取整体的1/4为研究对象,楼盖平面布置情况、控制截面及各参数,见图1。算例分析时,以中柱两侧各1/2柱距范围为中计算单元,以板边到边柱另一侧1/2柱距范围为边计算单元,计算单元划分、板带划分和弯矩控制截面位置[14]参见图1。
为保证后续分析的正确性,首先从单元形式、网格大小和单元长宽比等方面进行了大量验证分析。下面用2个算例来进行说明。
算例1为均布荷载作用下四角点支撑矩形实心板,模型参数为:均布荷载q=104N/m2,l1=l2=8.0 m,混凝土弹性模量E=3×1010N/m2,泊松比μ=0.2,实心板厚0.3 m。将广义简支边与列维(M.Levy)解结合,导出无穷联立方程组[15],本文取用前50项联立求解,获得柱上板带及跨中板带跨中正弯矩值的理论解析解。理论解析解与有限元计算结果见表1。通过对比发现,有限元数值计算结果和解析解非常吻合,特别是网格大小采用0.1 m、单元类型采用六面体8节点减缩积分单元(C3D8 R)的1/4板格模型,可以很好地兼顾计算效率和精度。
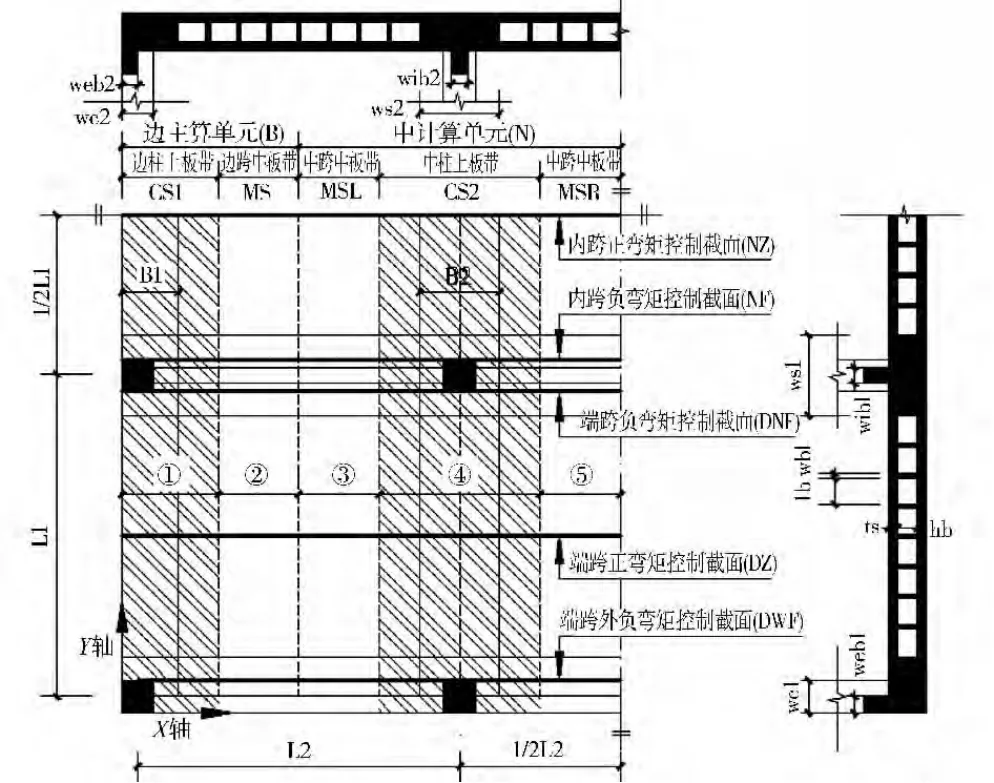
图1 空心板 柱结构的平面、剖面图
对于空心楼盖,顶板和底板较薄(0.05 m),划分两层后使六面体单元的长宽比可能较大。为验证长宽比对计算精度的影响,算例2为均布荷载作用下的不同边界条件的箱型截面梁,对比分析实体单元模型的计算结果与Ti moshenko梁单元的计算结果。模型参数为:箱型截面宽0.83 m,高0.4 m,壁厚0.05 m,均布荷载q=6.024×103N/m2(等效线荷载为5×103N/m),l=8.0 m,材料弹性模量E=3×1010N/m2,泊松比μ=0.2。不同单元计算结果对比见表2。通过对比发现,随着单元长宽比的增加,实体单元与Ti moshenko梁单元计算结果的误差有所增大,但弯矩的误差明显小于挠度的误差。当长宽比不超过4时,实体单元所得结果均与梁单元非常接近。考虑到本文后续分析仅关心弯矩分配比例,因此采用最大网格尺寸0.1 m以使单元长宽比不超过4,足以满足精度要求。

表1 有限元计算结果与解析解的对比

表2 实体单元长宽比对计算精度的影响
2 空心板与实心板弯矩分布规律对比
两块各支座均有梁的空心楼盖和实心楼盖的参数相同(l2/l1=1.0,μ1=1.0,βt=0.58),其中空心楼盖空心率(ρ)为30%。通过数值分析得到的各控制截面的弯矩分配系数如表3所示,表中板带编号见图1。
从表3可以得到以下结论:1)对于空心板,边计算单元与中计算单元各弯矩控制截面的弯矩分配差距很小,可以认为一致。这一结论与实心板类似,为直接设计法用于空心楼盖提供了前提条件[16]。2)通过对比空心楼盖和实心楼盖各弯矩控制截面所分得的弯矩比例,可以发现,虽然在支座处,由于柱和从属方向实心梁的约束,实心板与空心板各板带在支座处弯矩分布相差不大,但由于楼板刚度截面削弱,梁却承受了更多的弯矩,并且跨中位置的这种差距比支座截面位置体现得更显著,空心楼盖跨中截面柱上板带梁所承担的弯矩比实心楼盖高10%。
从以上对特定参数的空心板和实心板的对比分析可以看出,实心板和空心板在竖向荷载下的弯矩分布略有不同,需要做进一步的分析。

表3 空心板与实心板各弯矩控制截面弯矩分配系数计算值
3 柱(或柱帽)尺寸对弯矩分布的影响
文献[14]指出,直接设计法中弯矩控制截面弯矩在柱上板带板、柱上板带梁及跨中板带间的分配比例主要源于采用瑞雷 里兹(Rayleigh-Ritz)能量法求解薄板弯曲得到的近似解。在ACI318规范中,为了避免读取误差将原来的光滑曲线改为更易于用数学方式和表格表述的双线性函数。
瑞雷 里兹(Rayleigh-Ritz)能量法对板格边界条件作了一定的近似,不考虑柱子截面尺寸并假定为一点,这与实际情况不符合。文献[16]初步讨论了实心板中柱(或柱帽)尺寸对弯矩分布的影响,表明由于柱(或柱帽)的存在,能明显改变板带(板格)的边界条件,对板带的约束产生影响,直接设计法的分配系数至今没有考虑这种影响。柱(或柱帽)尺寸对空心楼盖弯矩分布的影响更是无人研究。
各算例选用最常用的板格边比(l2/l1)为1.0的内板格。对于无梁空心楼盖,按照文献[5]的构造要求设置相应宽度的柱轴线实心区域,算得梁板相对抗弯刚度比(μ1)等于0.218。空心楼盖设计时,为了体现其在增加有效层高上的优势,普遍不设立明梁或仅设置腹板高度很小的宽扁梁,对于l2/l1为1.0的空心楼盖来说,μ1不会大于1;一般的工程项目,柱跨比(c/l)不会超过0.2。综合以上各因素后,本文算例的μ1取0.218和1.0两种情况,每种情况下柱跨比取0到0.2、空心率取0(实心楼盖)和40%。分析结果见图2。

图2 柱尺寸效应
从图2可以看出:1)随着柱跨比(c/l)增加,弯矩控制截面负弯矩承担总设计弯矩M0的比例缓慢下降,μ1=0.218时,实心板从63.4%下降至56.7%,空心板从63.8%下降至55.9%;μ1=1.0时,实心板从66.7%下降至61.4%,空心板从65.4%下降至57.9%,空心板下降的比例更大。负弯矩的变化主要体现在柱上板带和柱上板带梁上;2)随着柱跨比增加,弯矩控制截面正弯矩承担总设计弯矩M0的比例缓慢上升,μ1=0.218时,实心板从31.1%上升至39.1%,空心板从31.3%上升至39.9%;μ1=1.0时,实心板从34%上升至40.2%,空心板从29.5%上升至37.6%,空心板上升的比例更大。正弯矩的变化主要体现在柱上板带梁和跨中板带上。通过对比还可以发现,空心楼盖截面弯矩相较于实心楼盖对柱跨比(c/l)的变化有更大的敏感性。
应该注意到,总设计弯矩值M0是按照净跨计算的[5],对于内跨,规范规定:跨中正弯矩设计值取0.35 M0;支座截面负弯矩设计值取0.65 M0,根据以上的对比分析,规范取值偏负弯矩值的上限,偏正弯矩值的下限,但正弯矩值的误差在5%左右。因此,当柱跨比(c/l)不大于0.2、梁板相对抗弯刚度比(μ1)不大于1.0时,规范取值造成的误差是可以接受的,此时不需要单独考虑柱(或柱帽)尺寸对弯矩一次分布的影响。
4 空心率(ρ)对二次弯矩分配系数的影响
根据文献[5]表5.4.7,主要研究当l2/l1分别等于0.5、1.0和2.0时,在不同空心率(ρ=0%、25%、30%、35%和40%)下,截面弯矩分配与梁板相对抗弯刚度比(μ1)的关系。算例柱跨比(c/l)均为0.1。
4.1 柱上板带负弯矩分配系数
如图3,当l2/l1=0.5时,柱支撑板主要以计算方向(长边方向)的板带整体受弯为主,不论空心率的大小,柱上板带负弯矩分配系数与实心板近似,与直接设计法系数吻合且偏安全;当l2/l1等于1.0及2.0时,空心楼盖的分配系数随着空心率的不同略有区分,但变化都不大,可以认为由于柱子和柱轴线实心区域的约束,柱上板带负弯矩分配系数和实心板类似。但当l2/l1≥1.0时,直接系数法取用的柱上板带负弯值偏下限,特别是当l2/l1=2.0时与计算值有较大的差距,尤其是工程中常见的μ1小于1的情况更为明显。建议对于l2/l1=1.0的空心楼盖,当μ1≥1时,柱上板带应承受支座截面负弯矩的80%;当μ1=0时,柱上板带应承受支座截面负弯矩的85%;当0<μ1<1时,可按线性插值确定柱上板带应承担的支座截面负弯矩值。对于l2/l1=2.0的空心楼盖,当μ1≤1时,柱上板带应承受全部支座截面负弯矩值;当μ1=4时,柱上板带应承受支座截面负弯矩的80%;当1<μ1<4时,可按线性插值确定柱上板带应承担的支座截面负弯矩值。当l2/l1=2.0时,总弯矩M0较小,截面配筋可能受最小配筋率控制[14],但仍应以建议值作验算。
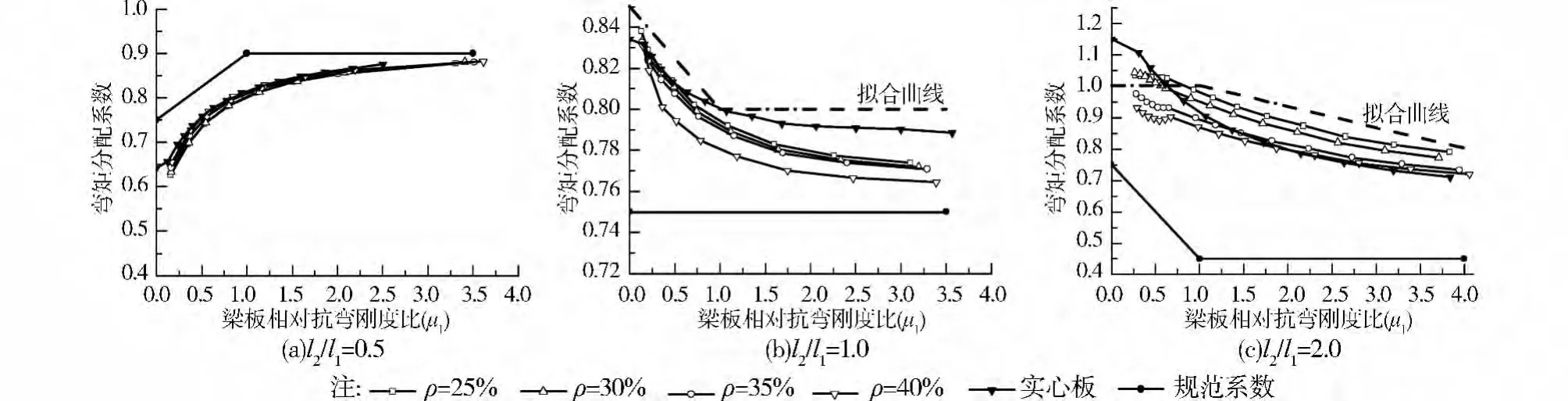
图3 空心率对柱上板带负弯矩分配系数的影响
4.2 柱上板带正弯矩分配系数
正如在第1小节的算例分析一样,由于空心楼盖截面刚度的削弱,对于跨中截面来说,柱上板带部分相应比实心板承担更多的弯矩,并且随着空心率的增加,柱上板带正弯矩分配系数进一步增加。如图4,对于l2/l1=0.5及l2/l1=1的空心楼盖,当μ1<1.0时,规范取值是合理的,当μ1>1时,规范取用的柱上板带正弯矩比例偏低,但与计算值之间的差距均在5%以内,可以继续采用规范值。对于l2/l1=2的空心楼盖,可以发现无论是实心板还是空心板,计算结果与规范值之间都有很大的差距,并且空心率对弯矩分配比例也有明显的影响。因此建议,对于实心楼盖,柱上板带应承受跨中截面正弯矩的60%;对于ρ=40%的空心楼盖,当μ1=0时,柱上板带应承受跨中截面正弯矩的60%,当μ1≥1时,柱上板带应承受跨中截面正弯矩的75%,当0<μ1<1时,可按线性插值确定柱上板带应承担的跨中截面正弯矩值。
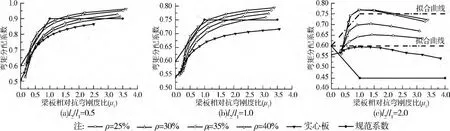
图4 空心率对柱上板带正弯矩分配系数的影响
4.3 柱上板带梁弯矩分配系数
如图5所示,无论l2/l1的值,当μ1>1时,梁分担的弯矩基本在柱上板带的85%左右。然而,对于工程中常见的μ1≤1的情况,由于直接设计法采用了线性插值,导致梁弯矩的查表值小于计算值,并且随着l2/l1的减小,梁实际承担的弯矩值比查表系数值高得更多,为方便设计,建议将拐点“μ1=1”偏安全地设为“μ1=0.5”。

图5 空心率对柱上板带梁弯矩分配系数的影响
5 端板格弯矩分配
5.1 总弯矩在支座截面和跨中截面的分配(一次分配)
端板格受力复杂,外支座与第一内支座对板系条带的约束程度不同,端跨跨度方向的弯矩分布一般是不对称的,分布形状主要取决于外柱的等效相对抗弯刚度其中:为外柱等效抗弯刚度;Kb=4EcbIb/l1为梁抗弯刚度;Ks=4EcsIs/l1为板抗弯刚度;为柱抗弯刚度;为梁抗 扭刚度。
ACI318规范针对端板格外端负弯矩(DWF)、跨中正弯矩(DZ)和第一内支座负弯矩(DNF)分别用式(1)~(3)[14]计算。
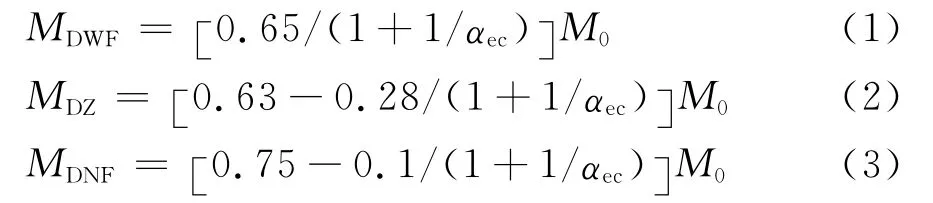
ACI318规范直接设计法中对于端板格一次弯矩分配系数就是对以上3个公式按不同几何尺寸和支座条件分析后确定的。针对空心率为35%的3种板格边比的端板格,分析了板格各控制截面弯矩分布与外柱等效抗弯刚度(αec)的关系,计算结果如图6所示。
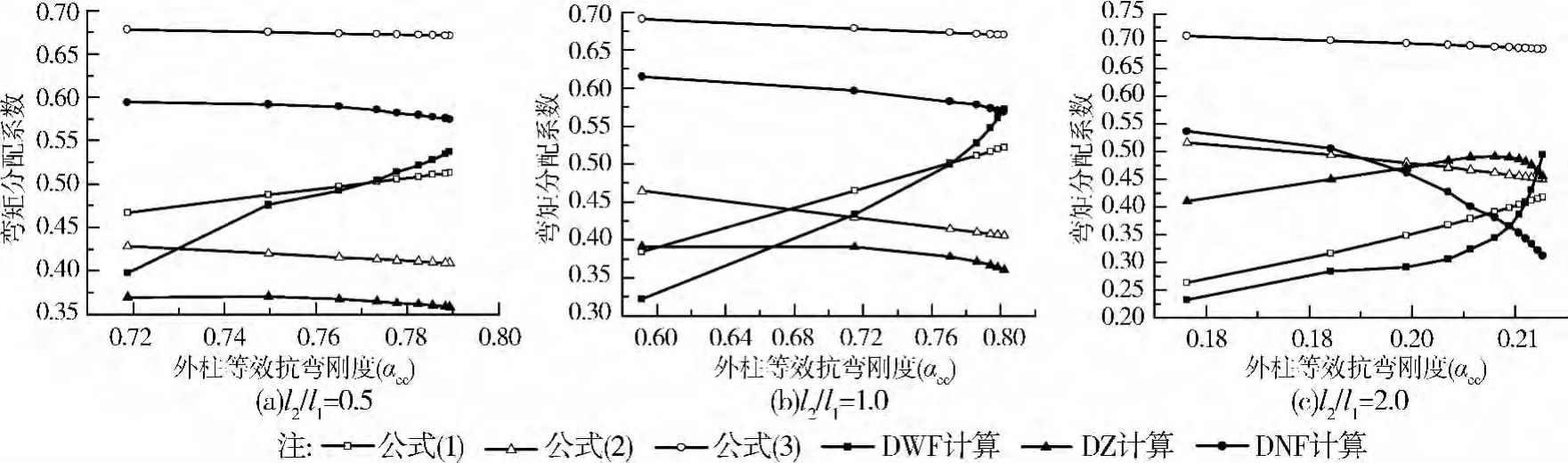
图6 外柱等效抗弯刚度与截面弯矩分配的关系
通过图6可以发现,空心楼盖端板格3个弯矩控制截面一次弯矩分配系数与外柱等效抗弯刚度有直接关系:端支座负弯矩计算值与式(1)差距很小;跨中截面正弯矩计算值与式(2)差距也不大;差别较大的是内支座负弯矩,特别是当l2/l1=2.0时,计算值与式(3)差距超过15%,公式值均偏安全。考虑到内跨支座负弯矩为固定值0.65 M0[5],又由于支座处钢筋均采用拉通布置即按照不平衡弯矩的大值配筋,因此没有必要重新拟合端跨内支座负弯矩计算式,可以仍按照ACI推荐的式(3)计算。
对于总弯矩在端跨各控制截面上的分配,规范虽列出了5类支座约束条件下的分配比例,但过于粗略,总弯矩的一次分配是否准确直接影响控制截面弯矩在柱上板带板、柱上板带梁及跨中板带上的弯矩分配。因此,鉴于端板格受力的复杂性,笔者建议在一次弯矩分配时,应避免直接查表,而应根据外柱等效抗弯刚度用式(1)~(3)计算。
5.2 端板格外支座负弯矩的分配(二次分配)
图7是在其他条件不变仅改变边梁尺寸,考察边梁相对抗扭刚度比(βt)对端板格外支座处各控制截面二次弯矩分配的影响。图中DWF为端板格外支座负弯矩截面;CS为柱上板带;MS为跨中板带,三者弯矩值关系为:。当边梁抗扭刚度很小甚至没有边梁时,中间板带与柱之间相当于没有约束,中间板带弯矩应为零,此时,柱上板带应承担全部的外支座负弯矩。增大边梁抗扭刚度均可使中间板带弯矩增加,但当板格比分别为0.5、1.0时边梁抗扭刚度对柱上板带所承担的弯矩值影响较小。虽然板格边比为2.0时,柱上板带弯矩比例有一定的变化,但由于此时短跨方向承担的弯矩小,因而实际承担的弯矩值变化是有限的,始终处于很低的水平。所以当进行结构设计时,柱上板带承担的弯矩值可以采用一个很小的边梁抗扭刚度(如It=0.01)用式(1)直接进行计算,支座截面负弯矩的剩余部分相应地由跨中板带承担。这样计算的柱上板带负弯矩值比实际值稍偏大,但考虑到边梁带裂缝工作,减小了对跨中板带的约束,意味着柱上板带承担的弯矩值会增加,设计时采用一个稍偏大的弯矩值反而是偏安全的。
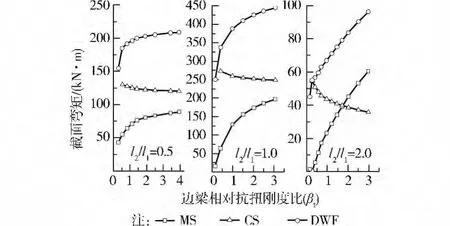
图7 边梁相对抗扭比对外端截面弯矩分配的影响
综合第3~5章算例分析,建议直接设计法查表系数应做调整,调整后的空心楼盖总设计弯矩M0的一次分配系数见表4,空心楼盖柱上板带及梁弯矩的二次分配系数见表5。表中参数的中间值采用线性插值,对于二次分配,跨中板带承担的弯矩由控制截面总弯矩扣除柱上板带承担的弯矩后得到。

表4 空心楼盖一次弯矩分配建议
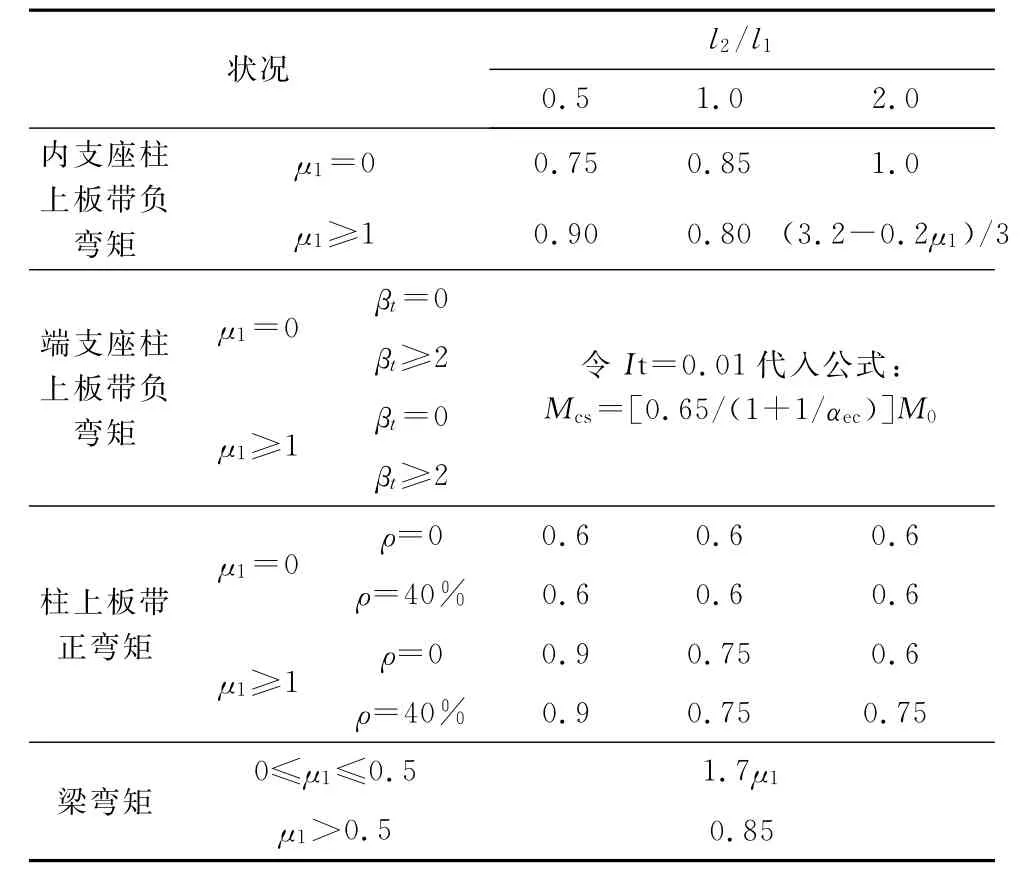
表5 空心楼盖二次弯矩分配建议
6 结论
通过大量的算例分析,可以得到以下结论:
1)竖向荷载下,空心楼盖与实心楼盖在边计算单元和中计算单元间以及各计算单元内的弯矩分布规律类似,差异主要体现在跨中正弯矩的分配上。
2)当μ1不大于1以及c/l不大于0.2时,柱(或柱帽)的尺寸效应对截面弯矩一次分配的影响可以忽略。
3)空心楼盖直接设计法不能完全沿用已有规范中关于实心楼盖的分配系数,调整后的空心楼盖直接设计法系数见表4及表5。
4)端板格一次弯矩分配及二次弯矩分配采用本文提出的方法可以较好地兼顾实用性和准确性。
[1]赵考重,李自然,王莉,等.装配箱混凝土空心楼盖结构受力性能试验研究[J].工程力学,2011(Suppl1):145-150.Zhao K Z,Li Z R,Wang L,et al.Experi mental study on mechanical perfor mance of assembly box concrete hollow floor str ucture with assembly style [J].Engineering Mechanics,2011(Suppl1):145-150.
[2]周绪红,陈伟,吴方伯,等.混凝土双向密肋装配整体式空心楼盖刚度研究[J].建筑结构学报,2011,32(9):75-83.Zhou X H,Chen W,Wu F B,et al.Study on stiff ness of assembled monolithic concrete hollow floor with t woway ribs[J].Jour nal of Building Str uctures,2011,32(9):75-83.
[3]Chung L,Lee S H,Cho S H,et al.Investigations on flexural strength and stiff ness of hollow slabs [J].Advances in Structural Engineering,2010,13(4):591-601.
[4]胡萍,杨伟军,张振浩,等.蜂巢芯空心楼盖足尺试验研究及有限元分析[J].建筑结构,2012,42(1):85-90.Hu P,Yang W J,Zhang Z H,et al.Full-scale test study and finite element analysis on honeyco mbed-core hollow floor[J].Building Structure,2012,42(1):85-90.
[5]JGJ/T 268—2012现浇混凝土空心楼盖技术规程[S].北京:中国建筑工业出版社,2012.
[6]周玉,韩小雷,季静.宽扁梁楼盖结构计算方法[J].华南理工大学学报:自然科学版,2004,32(4):78-81.Zhou Y,Han X L,Ji J.Calculation method for wide-flat beam-slab str uct ures [J].Jour nal of South China University of Technology:Natural Science Edition,2004,32(4):78-81.
[7]Ibrahim A,Salim H,El D,et al.Moment coefficients for design of waffle slabs with and wit hout openings[J].Engineering Str uctures,2011,33(9):2644-2652.
[8]袁俊杰.拟梁法和直接设计法在现浇混凝土空心楼盖结构分析中的应用[J].铁道科学与工程学报,2008,5(3):78-82.Yuan J J.Analysis of cross beams method and direct design method applied to cast-in-situ concrete hollow floor str ucture [J].Jour nal of Rail way Science and Engineering,2008,5(3):78-82.
[9]郭楠,郑文忠.板-柱结构在竖向荷载作用下的弯矩分布规律研究[J].工业建筑,2008(Supll1):174-177.Guo N,Zheng W Z.Research on moment distribution law of plate-colu mn str ucture subject to vertical loads[J].Industrial Constr uction,2008(Suppl1):174-177.
[10]刘文珽,姚谦峰.垂直荷载作用下板柱结构计算方法的比较与分析[J].建筑结构,2009,39(8):56-59.Liu W T,Yao Q F.Discussion on analysis methods f or flat slab str uctures under vertical loading[J].Building Str uct ure,2009,39(8):56-59.
[11]李海涛,苏小卒,刘立新.柱支承现浇空心楼盖的直接设计法建议[J].武汉理工大学学报,2009,13(19):88-92.Li H T,Su X Z,Liu L X.Direct design method advice of column-supported cast-in-situ hollow floor[J].Journal of Wuhan University of Technology,2009,13(19):88-92.
[12]Li H T,Andrew J D,Liu L X,et al.Mo ment transfer factors f or colu mn-supported cast-in-situ hollow core slabs[J].Journal of Zhejiang University:Science A,2012,13(3):165-173.
[13]Huang C T,Wang Z J,Qu Y Y.Parameters analysis with regar d to the hollow floor based on the ABAQUS secondar y develop ment [C]// The 2nd Inter national Conference on Str uct ures and Building Materials.Hangzhou,China,2012:1337-1342.
[14]Park R,Gamble W L.Reinforced concrete slabs[M].2 ed.John Wiley and Sons,1999.
[15]Kardomateas G A,Phan C N.Three-di mensional elasticity solution for sand wich beams/wide plates wit h orthotropic phases:The negative discri minant case[J].Journal of Sand wich Structures and Materials,2011,13(6):641-661.
[16]Gamble W L.Moments in Beam Supported Slabs[J].Jour nal of The American Concrete Institute,1972,69(3):149-157.

