人眼眼底成像系统中自适应光学像差校正控制模型研究

贾皓丽 沈建新* 钮赛赛

1(南京航空航天大学机电学院，南京 210016)2(上海航天控制技术研究所，上海 200233)

人眼眼底成像系统中自适应光学像差校正控制模型研究

贾皓丽1沈建新1*钮赛赛2

1(南京航空航天大学机电学院，南京 210016)2(上海航天控制技术研究所，上海 200233)

对于自适应光学人眼眼底成像系统，由于人眼波前像差具有动态特性，为获得清晰、高分辨率的眼底图像，变形镜必须能够实时跟踪并补偿人眼中随时间变化的像差信息。本研究探讨自适应光学像差校正控制技术，基于自动控制理论建立自适应光学连续系统模型，分析基于纯积分、比例-积分和Smith预补偿控制器下的控制系统模型及其控制性能。在自行构建的成像系统自适应光学平台上，对10只受试人眼动态像差样本进行像差校正实验。与校正前的像差((0.862±0.088)λ，λ为0.785 μm)比较，纯积分控制、PI控制和Smith预补偿控制这3种方法的校正后像差((0.154±0.033)λ、(0.133±0.026)λ、(0.103±0.011)λ)均显著降低(P<0.05)，表明各种控制器的像差校正系统均具备一定的像差校正能力。单因素方差分析的结果表明，Smith预补偿控制的校正后像差显著低于纯积分控制和PI控制方法，表明Smith预补偿控制器下校正后的像差具有最大的显著差异，即具有最好的像差校正效果。Smith预补偿控制模型可为实时校正人眼动态像差进而获取人眼眼底图像提供理论依据。

自适应光学；人眼像差；像差校正；Smith预补偿控制器

引言

人眼光学系统十分复杂，人眼像差是限制眼底成像设备对眼底清晰成像的主要因素[1-2]。在成像过程中，借助自适应光学技术，在理论上可以有效地校正从眼底出射的畸变波前，从而获得清晰的眼底图像[3-5]。但是要补偿随时间动态变化的畸变波前，像差的实时校正效果会受到较大限制，特别是在人眼自适应光学中，对眼底的高分辨率成像非常不利[6]。

自适应光学控制系统通常是一个延迟控制系统[7]。一方面，会导致波前传感器探测得到的波前信息不能实时准确地反映残余波前的信息；另一方面，变形镜控制信号的响应也不能实时地对畸变波前进行补偿，从而造成系统超调和振荡，系统的稳定性和动态响应特性也必然会不理想，最终影响人眼波前像差的校正效果。这类具有延迟特性的控制过程被公认为是较难控制的过程，其控制难度随延迟时间占整个动态控制过程的增加而增加。

目前，自适应光学系统中应用最多的控制算法是基于自动控制理论的控制算法，比如纯积分控制、最小拍控制等算法[8]；随着自动控制理论的进一步发展，也出现了一些基于现代控制理论的控制算法，比如自适应控制、神经网络控制等算法[9]。总之，这些控制算法都在满足闭环控制稳定性、不产生振荡等要求的基础上，尽可能提高系统的有效控制带宽。

为优化自适应光学系统的控制效果，可以通过提高Hartmann-Shack波前传感器中CCD采样频率，或采取提高控制计算机性能等改进硬件的方法，减少控制系统延迟时间。本研究主要是在不加大硬件复杂度的基础上，通过设计合理的控制器或优化控制算法来改善自适应光学系统的像差校正控制效果，着重分析基于纯积分[10]、比例-积分(PI)和Smith预补偿控制器下的控制系统模型及其控制性能。通过对模拟眼静态像差和受试者动态像差的校正实验，表明在Smith预补偿控制器下的系统快速性最好，可为实时校正人眼动态像差进而获取人眼眼底图像提供理论依据。

1 方法

1.1自适应光学系统闭环控制模型

自适应光学系统闭环控制模型的结构如图1所示。闭环控制模型主要包括了波前传感器、变形镜和控制器3个模块。其中，φorg、φcor和φres分别是人眼的原始畸变波前、变形镜产生的校正波前和校正之后的残余波前，满足φres=φorg-φcor；w是波前测量过程中引入的误差噪声向量，g是传感器探测得到的波前斜率值向量，u是由控制器输出的变形镜控制电压/信号向量。自适应光学闭环控制的目的就是使残余波前φres的相位达到最小，使成像设备能对眼底清晰成像。在自适应光学的经典控制问题中，通常满足以下假设：

1)由于模型中控制器不会改变原始畸变波前φorg，所以对自适应光学控制器的设计可归纳为标准的抗扰控制问题；

2)假设变形镜是连续型线性时不变系统，而波前传感器是离散型线性时不变系统，其离散采样时间为T；

3)假设波前斜率向量g处理、控制电压向量u计算能在同一采样周期T内完成。

图1 自适应光学系统闭环控制模型结构框图Fig.1 Block diagram of closed-loop control model of adaptive optics system.

波前传感器模块包含了波前探测和波前计算两个环节，波前探测环节的传递函数为GWFS(s)=(1-e-Ts)/Ts，它的输出和输入信号都是连续信号，波前计算环节是纯延迟环节，传递函数为GWFC(s)=e-Ts，它的输入是连续信号，而输出是周期为T的离散信号；控制器模块包含了变形镜控制信号计算环节，控制器的时间特性主要取决于实时补偿设计，这也是自适应光学系统控制研究的主要内容，传递函数记为GC(s)；变形镜模块主要包含高压放大和变形镜响应环节，传递函数都记为1，即GHVA(s)=1和GDM(s)=1，它们的输入和输出都是连续信号。因此，自适应光学系统是一个集数字与模拟信号、连续与离散信号混合为一体的反馈回路控制系统。

1.2自动控制理论下的连续系统模型研究

对自适应光学系统的闭环控制研究从基于连续系统模型的方法展开，根据连续系统的性能参数指标比较、带宽优化分析等方式，最终确定控制计算环节的数字化控制器。自适应光学连续系统的框图如图2所示。

图2 自适应光学人眼像差闭环校正控制系统框图Fig.2 Block diagram of closed-loop human eye aberration correction control system

根据连续系统模型的原理，连续系统的开环、闭环传递函数分别为

(1)

(2)

从式(1)和式(2)可以看出，对连续系统模型研究的主要内容是确定合适的控制器GC(s)，使得控制系统的工作性能达到最优。控制器设计需满足以下基本要求[11]：在时域内，对于阶跃输入信号，闭环系统应具有最优的动态响应和零误差稳态响应；在频域内，系统的正弦输入信号响应能取得较大系统带宽，并确保闭环幅频特性的谐振峰值小于3 dB、开环系统幅值裕量大于6 dB、相位裕量在30°～70°内，从而分别提高闭环控制系统的抗扰能力和稳定性。传统的自适应光学控制算法常采用简单的纯积分控制器，目的是降低算法的复杂性且已在系统中实现，但由纯积分控制带来的时间滞后将会降低系统稳定裕度，因此在不失简易性的基础上可考虑其他PID控制器或者采用补偿系统纯滞后Smith预补偿控制器对自适应光学系统的控制性能。

1.2.1纯积分控制器

首先考虑最简单的纯积分控制环节，其传递函数为

(3)

KI值选取会直接影响系统的开环幅值穿越频率和相位裕量，如果要增大纯积分控制时的相位裕量，必须减小增益参数KI，这意味着系统的开环带宽(开环传递函数增益为0 dB时的频率，即幅值穿越频率ωc)和开环增益都随之减小，会导致系统响应速度降低。将式(3)代入式(1)，根据开环传递函数的尼柯尔斯(Nichols)图(见图3)，可知当25≤KI≤52时，系统满足控制器的设计要求，比如KI=52，幅值裕量和相位裕量分别为6.49dB和46°。当KI>52时，闭环峰值响应增大，会导致系统产生振荡；当KI<25时，相位裕量过大，由于稳定程度过好，会造成系统动态过程缓慢。

1.2.2比例-积分控制器

PI控制器可以通过引入积分控制作用来改善系统的稳态性能，同时通过比例控制作用来调节积分作用所导致相角滞后对系统的稳定性和动态过程带来的不利影响，即改善系统的相位裕量。PI控制环节的传递函数为

(4)

由此可见，改变KP值(|KP|<1)可以调节相应纯积分环节时的幅值穿越频率和相位裕量。图4是在图3中的纯积分控制基础上添加不同比例控制增益后的系统开环传递函数Nichols图。可以看出，选择适当的增益参数KP，相对于纯积分控制一方面可以减小闭环峰值响应，另一方面可以在系统稳定条件之下提高幅值裕量和相位裕量，比如当KI=25、KP=-0.05时，幅值裕量和相位裕量分别提高至11.6 dB和66°；因此也可将纯积分控制时的不稳定系统的幅值裕量和相位裕量调整至稳定条件范围内，比如当KI=10、KP=-0.2时，幅值裕量和相位裕量分别为11.2 dB和70°，满足系统稳定条件。总之，合理选择KP和KI，可使系统控制更加灵活、品质更优，此时的PI控制会优于纯积分控制。

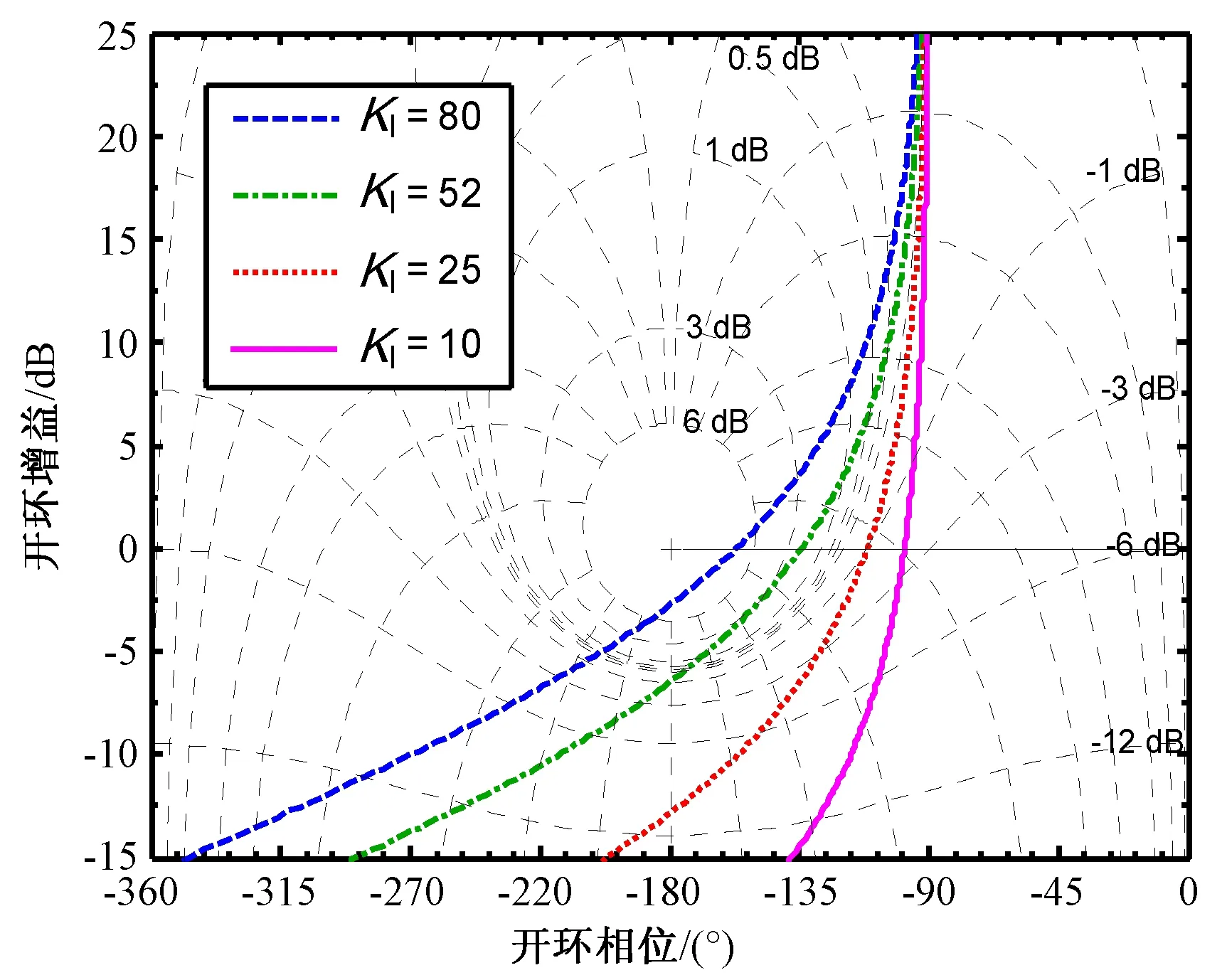
图3 纯积分控制连续系统开环传递函数Nichols图Fig.3 Nichols of open-loop transfer function with pure integral control.

1.2.3Smith预补偿控制器

图4 比例-积分控制连续系统开环传递函数Nichols图Fig.4 Nichols of open-loop transfer function with Proportional integral control

(5)

式中，KSI≤100。

图5 基于Smith预补偿控制器的系统模型方框图 Fig.5 Block of control model based on Smith pre-compensation control.

图6是基于Smith预估补偿器的系统开环传递函数Nichols图。可以看出，当KSI取不同值时，闭环幅频特性的谐振峰值都不超过0 dB，表明系统具有良好的瞬时响应品质，但为了维持稳定系统具有适当的相位裕量，KSI的取值至少大于35，比如当KSI=35时，幅值裕量和相位裕量分别为12.6 dB和70°，恰好满足系统稳定条件。

图6 Smith预补偿控制连续系统开环传递函数Nichols图Fig.6 Nichols of open-loop transfer function with Smith pre-compensation control.

1.3连续系统控制模型性能分析

为评价各种控制器对连续系统控制性能的好坏，主要是在闭环带宽相等的基础上分别对不同控制器下连续系统的谐振峰值、相位裕量、幅值裕量、输入信号作用下的单位阶跃响应等性能进行分析。设置纯积分控制器的参数KI=52，PI控制器的参数为KI=50、KP=0.1，Smith预补偿控制器的参数为KSI=72.5，此时3种控制器下的系统闭环带宽均为18.7 Hz左右。幅值裕量分别为kGI，g=6.48 dB、kGPI，g=7.99 dB和kGSIM，g=8.34 dB，相位裕量分别是γGI，c=43.31°、γGPI，c=52.55°和γGSI，c=63.37°。可见，在相同的闭环带宽条件下，纯积分控制的系统幅值裕量和相位裕量都最小，而Smith预补偿控制的系统幅值裕量和相位裕量最大，因此不管从幅值裕量还是从相位裕量角度看，Smith预补偿控制的系统稳定性能明显优于其余两种控制方法。

闭环带宽相同的系统其闭环特性并不相同，图7是连续系统闭环传递函数频域响应特性Bode图。可以看出，在低频段，系统的频域特性几乎相同；而在中频段，纯积分和PI控制的系统幅频响应存在谐振峰值Mr，分别为2.97和1.21 dB，但均能满足控制器设计的基本要求(小于3 dB)，Smith预补偿控制器下的系统不产生谐振峰值，表明系统快速性较好；对于高频信号，Smith预补偿控制器相对于其他控制器具有更小的抑制作用，在自适应光学系统中表现为能补偿更多的高频像差。

图7 各种控制器下连续系统的闭环传递函数频域特性Bode图Fig.7 Bode diagram of closed-loop transfer function with different controllers.

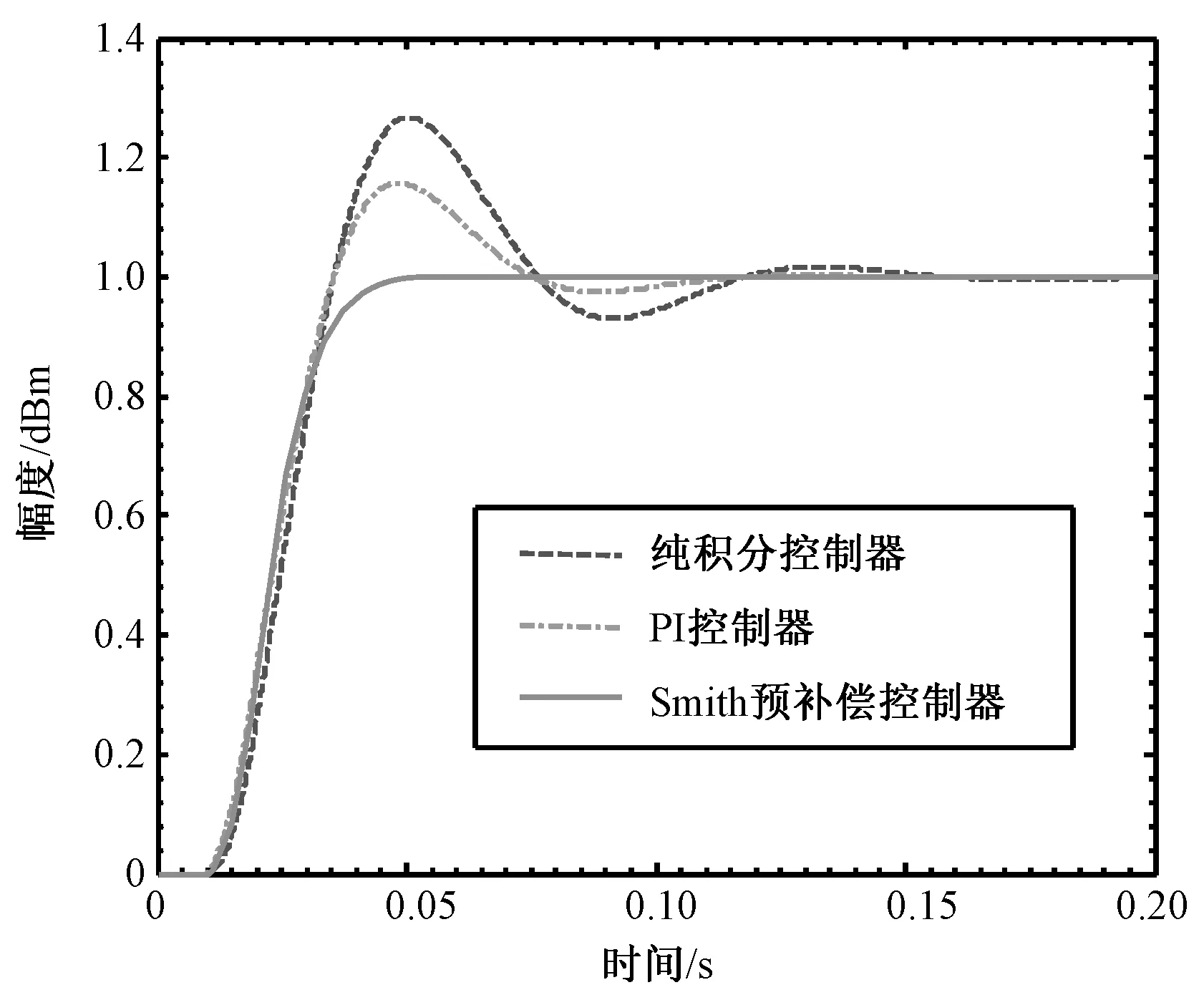
图8 各种控制器下连续系统单位阶跃响应比较Fig.8 Comparison of unit step response with different controllers

图8是各种控制器下的系统在输入信号作用时的单位阶跃响应比较。可以看出，各种控制器下系统的稳态误差均为0，还可直观地看出各系统的延迟时间、上升时间和峰值时间非常接近，但Smith预补偿控制器下系统的调节时间和超调量远远低于纯积分和PI控制器下的系统，表明Smith预补偿控制的系统具有最快的响应速度，这与频域特性分析的结果一致。

1.4算法验证

利用自行构建课题组搭建的自适应光学实验系统，验证各控制器下人眼像差校正算法。通过实验的方法对比，分析在上述控制器下系统对像差的校正性能。实验系统原理如图9所示，除了自适应光学主体硬件外，还包括像差测量信标光源、孔径匹配、瞳孔定位跟踪等部分，系统能呈现像差测量和闭环校正两种工作状态，在实验时将待测的模拟眼或人眼放置在“眼”位置处。在闭环校正时，控制计算机根据像差的测量结果，再由上述讨论的控制器计算得出校正电压，对光路中像差进行校正，传感器实时测量残余像差，计算机根据残余像差计算电压，继续施加至变形镜，如此反复，形成闭环迭代校正。

在纯积分控制器下的校正算法中，取KI=35；在PI控制器下的校正算法中，取KI=40，KP=0.15；在Smith预补偿控制器下的校正算法中，取KSI=65。此时，在纯积分控制、PI控制、Smith预补偿控制下，自适应光学系统闭环带宽分别为12.3、13.9和15.8 dB。

在成像系统自适应光学平台上，采用以上控制参数配置的各波前校正算法对模拟眼静态像差和来自8位受试者的10只人眼像差样本进行像差校正实验。对于每种校正方法，校正前后的比较采用配对t检验。3种不同校正方法采用单因素方差分析(one-way ANOVA)。如果P<0.05，则认为被检验指标间存在显著性差异。

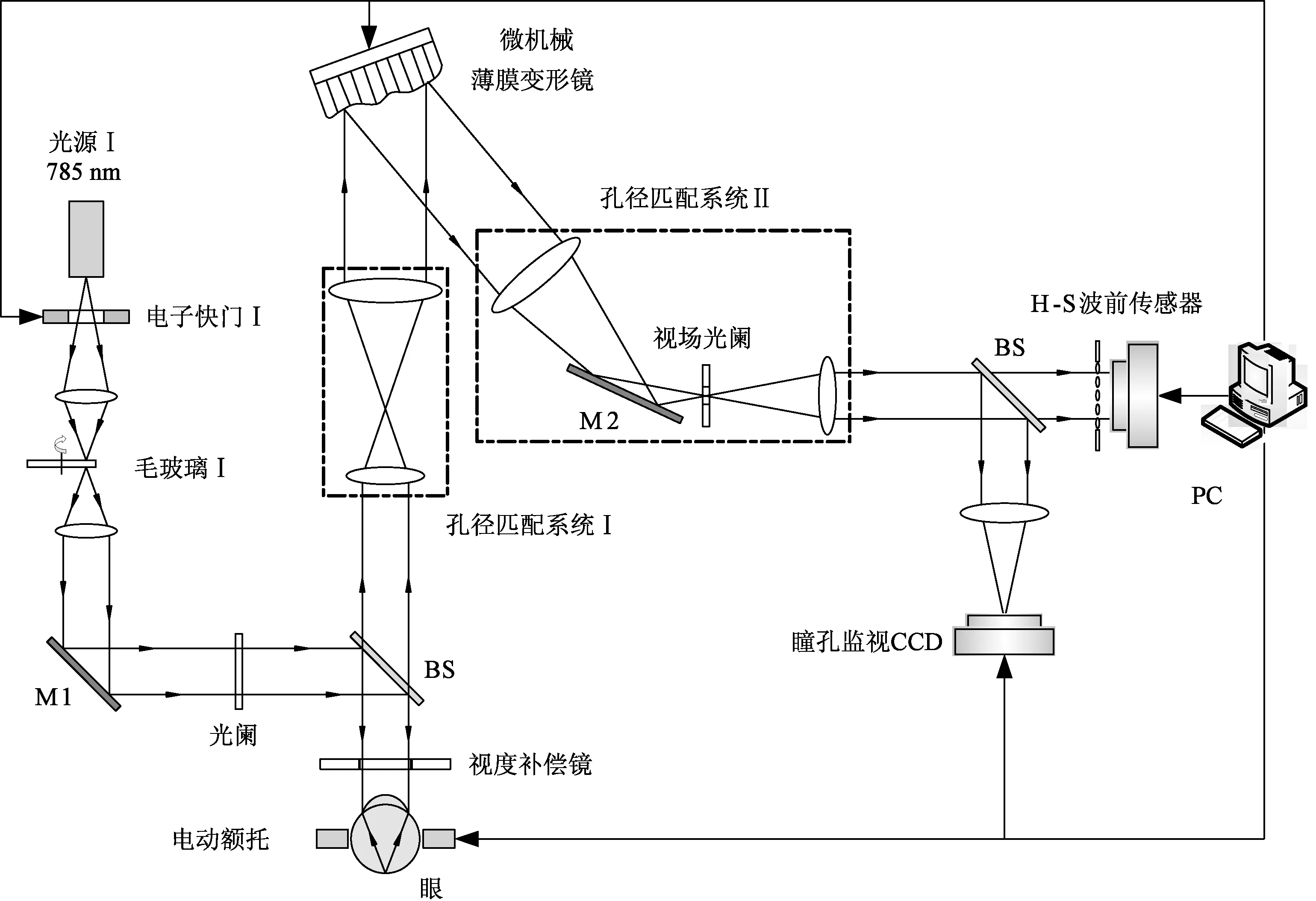
图9 自适应光学像差校正实验系统原理Fig.9 Schematic diagram of adaptive optical aberration correction experimental system

2 实验结果

模拟眼与受试者人眼像差用不同控制器校正前后的结果见表1。 经多次测定，模拟眼及10个受试者人眼像差样本采用不同控制器，像差校正前后的RMS均值比较如表1所示。 与校正前比较，纯积分控制、PI控制和Smith预补偿控制这3种方法的校正后像差均显著降低(P<0.05),表明各种控制器的像差校正系统均具备一定的像差校正能力。单因素方差分析的结果表明，Smith预补偿控制的校正后像差显著低于纯积分控制和PI控制的校正后像差，表明Smith预补偿控制器下校正后的像差具有最大的显著差异，即具有最好的像差校正效果。对于静态模拟眼像差，不同控制器下系统的像差校正能力比较接近。

表1 模拟眼与受试者人眼像差不同控制器校正前后结果比较

注：*P<0.05，与校正前比较；#P<0.05，分别与纯积分控制及PI控制比较

进一步以模拟眼和GSL人眼为例，图10中(a)和(b)展示了模拟眼和人眼像差在由不同控制器进行校正过程中残余像差RMS值随校正次数变化的曲线。可以看出，各控制器下的系统均能将像差校正至一稳定值，但是Smith预补偿控制器下的系统快速性最好。对模拟眼像差，Smith控制器下像差校正至稳定值的校正次数比其他控制器少2～3次；而对GSL人眼像差，Smith控制器比其他控制器少5～6次。

图10 3种控制器下波前像差校正性能比较。(a)模拟眼静态像差；(b)受试者GSL人眼动态像差Fig.10 Compared performance of aberration correction with different controllers. (a) Static aberration of model eye; (b) Dynamic aberration of subject GSL

图11是模拟眼均值像差采用Smith预补偿控算法校正前后的波前图和点扩散函数的分布，图12是受试者GSL人眼均值像差采用Smith预补偿控算法校正前后的波前图和点扩散函数分布，可以更直观地看出Smith预补偿控算法对静态像差和人眼动态像差均有较好的像差校正性能。校正后的残余像差RMS均值分别约为0.083λ和0.098λ，PSF图确定的成像系统图像质量评价参数斯特利尔比(SR)在像差校正后分别为0.78(校正前为0.4)和0.75(校正前为0.27)，表明对于模拟眼静态像差和人眼动态像差，通过Smith预补偿控算法均能将其校正至接近衍射极限。这说明，上述实验方法及结果可为实时校正人眼动态像差进而获取人眼眼底图像提供理论依据。

图11 模拟眼像差校正前后的结果对比。(a)校正前波前图；(b)校正前PSF图；(c)校正后波前图；(d)校正后PSF图Fig.11 Compared results before and after aberration correction on model eye. (a) Wavefront before correction; (b) PSF before correction; (c) Wavefront after correction; (d) PSF after correction

图12 GSL人眼像差校正前后结果对比。(a)校正前波前图；(b)校正前PSF图；(c)校正后波前图；(d)校正后PSF图Fig.12 Compared results before and after aberration correction on eye of subject GSL. (a) Wavefront before correction; (b) PSF before correction; (c) Wavefront after correction; (d) PSF after correction

4 讨论和结论

由自适应光学系统闭环控制模型在不同控制器下理论研究和实验结果可知，优化系统中的控制器确实可以提高系统的像差校正控制能力。通过对纯积分控制器、PI控制器和Smith预补偿控制器下系统的控制性能分析可知，采用Smith预补偿控制器，具有最快的响应速度，可以更好地改善系统的延迟效应。在实验过程中，对于校正静态像差，各种控制器下系统校正性能基本一致。这主要是由于静态像差的波动频率能控制在上述系统的闭环带宽内，系统工作的延迟效应不明显，基本能实现实时校正；而对于人眼动态像差，像差波动频率较高，采用Smith预补偿控制器的系统具有更大的带宽，能有效校正人眼像差中更多的高频像差，表明Smith预补偿控制器能一定程度上克服系统的延迟效应。纯积分控制器和PI控制器自身的频域特性，限制了其对人眼动态像差实时校正的能力。因此，采用Smith预补偿控制器的自适应光学闭环控制系统，意味着能更有效地实现人眼眼底视网膜图像的摄取。

对于人眼像差校正控制的研究，课题组接下来的工作将从两个方面展开：一方面是继续在自动控制理论的基础上研究Smith预补偿控制器，控制器改良及控制器中参数的优化设计将是研究重点；另一方面是从现代控制理论的角度出发，根据人眼像差特性，研究像差校正的最优控制问题，比如自适应控制、神经网络控制等算法。

本课题对自适应光学像差校正控制模型展开研究，主要是在不加大硬件复杂度的基础上，通过设计合理的控制器或优化控制算法来改善系统的控制效果。首先，在自动控制理论下介绍了自适应光学系统的闭环控制回路，并建立自适应光学连续系统模型；然后，根据连续系统的性能参数指标比较、带宽优化分析等方式，确定连续型经典控制器(包括纯积分、PI和Smith预补偿控制器)及其控制参数。最后，对模拟眼和动态人眼进行像差校正实验，对受试者人眼像差分别采用不同的控制器，对校正后的像差与校正前的像差进行显著性t检验，表明在Smith预补偿控制下的系统对人眼像差具有最显著的像差校正能力，可为实时校正人眼动态像差，进而获取人眼的眼底图像提供理论依据。

[1] Wang Li, Santaella RM, Booth M,etal. Higher-order aberrations from the internal optics of the eye [J]. Journal of Cataract and Refractive Surgery, 2005,31(8): 1512-1519.

[2] Thibos LN, Hong X, Bradley A,etal. Statistical variation of aberration structure and image quality in a normal population of healthy eyes [J]. J Opt Soc Am A, 2002,19(12): 2329-2348.

[3] Jason P, Hope MQ, Julianna EL,etal. Adaptive optics for vision science: principles, practices, design, and application [M]. Hoboken: John Wiley & Sons, Inc, 2006: 1-11.

[4] Liang Junzhong, William DR, Miller DT. Supernormal vision and high resolution retinal imaging through adaptive optics [J]. J Opt Soc Am A, 1997,14(11): 2884-2892.

[5] 凌宁, 张雨东, 饶学军, 等. 用于活体人眼视网膜观察的自适应光学成像系统[J]. 光学学报, 2004,24(9): 1153-1158.

[6] Liang Junzhong, Grimm B, Goelz S,etal. Objective measurement of the wave aberrations of the human eye with the use of Hartmann-Shack wave-front sensor [J]. J Opt Soc Am A, 1994,11(7): 1949-1957.

[7] Niu Saisai, Shen Jianxin, Liang Chun,etal. High-resolution retinal imaging with micro adaptive optics system [J]. Applied Optics, 2011,50(22): 4365-4375.

[8] 柳丛, 马彩文, 冯莉, 等. 自适应光学系统伺服控制回路的分析与设计[J]. 光子学报, 2008,37(1): 281-284.

[9] Correia C, Conan J M, Kulcsar C.etal.. Adapting optimal LQG methods to ELT-sized AO systems [C] //Clenet Y, Conan JM, Fusco T,etal, eds. 1st AO4ELT conference-Adaptive Optics for Extremely Large Telescopes. Paris: EDP Sciences, 2010: 07003P1-07003P6.

[10] Correia C, Raynaud HF, Kulcsar C,etal. Minimum-variance control for astronomical adaptive optics with resonant deformable mirrors [J]. European Journal of Control, 2011,17(3): 222-236.

[11] 余成波, 张莲, 胡晓倩, 等. 自动控制原理[M]. 北京: 清华大学出版社, 2009: 199-200.

[12] Ferrario D, Wildi F. Nulling interferometry and adaptive optics control system optimization [C] //Daniel RC, eds. Techniques and Instrumentation for Detection of Exoplanets II. Washington: SPIE， 2005: 59050Q1-59050Q12.

[13] 陈宗海, 杨晓宇, 王雷. 计算机控制工程[M]. 合肥: 中国科学技术大学出版社, 2008: 195-197.

AberrationCorrectionControlModelofAdaptiveOpticsintheFundusImagingSystem

JIA Hao-Li1SHEN Jian-Xin1*NIU Sai-Sai2

1(CollegeofMechanicalandElectricalEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China)2(ShanghaiInstituteofSpaceflightControlTechnology,Shanghai200233,China)

In an adaptive optics imaging system of human eye fundus, for the dynamic characteristic of human eye aberration, deformable mirror must be able to track and compensate the human eye aberration in time to achieve clear and high resolution fundus imaging. The technology of adaptive optics aberration correction control was studied, and an adaptive optics continuous system model was established according to the automatic control theory. The control system model and its control properties based on the pure integral, proportion integral, Smith pre-compensation were analyzed emphatically. The aberration correction experiments with dynamic aberration samples were canried out on a adaptive optics imaging system platform. And 10 human eyes were included in the experiments.Compared to the aberration ((0.862±0.088)λ, λ=0.785μm) before the correction, the aberration ( (0.154 ± 0.033) λ, (0.133 ± 0.026)λ, (0.103 ± 0.011)λ) with the pure integral control, PI control and Smith pre-compensation control were significantly lower (P<0.05). The above results indicated the aberration correction system with various controllers possessed a certain aberration correction capability. The ANOVA results showed that corrected aberrations with Smith pre-compensation control was significantly lower than the pure integral control and PI control method, which indicated that the aberration corrected with Smith pre-compensation controller had the maximum significant difference, that is the best effect of aberration correction. The Smith pre-compensation control model can provide theoretical basis for correcting human eye dynamic aberration to obtain human eye fundus image.

adaptive optics; human eye aberration; aberration correction; Smith pre-compensation controller

10.3969/j.issn.0258-8021. 2014. 01.006

2013-03-10，录用日期：2013-12-27

江苏省自然科学基金青年基金(BK2012380)；江苏省产学研联合创新资金(BY2012009)；中央高校基本科研业务费专项资金(NJ20120007)

R318.08

A

0258-8021(2014) 01-0037-08

*通信作者。E-mail: cadatc@nuaa.edu.cn