PIV和CFD在搅拌桨设计和优化中的应用
葛春艳 王嘉骏 顾雪萍 冯连芳
(浙江大学化学工程与生物工程学系,浙江杭州 310027)
目前,对于搅拌反应器的选型和设计主要依靠一些经验手段,尚未形成完整的理论体系。随着计算机技术的发展,计算流体力学CFD(Computational Fluid Dynamics)广泛应用于搅拌混合的研究,一旦CFD 方法能够成功模拟出搅拌槽内的三维流场,即可方便地获得流场随搅拌叶轮和搅拌槽的构型、尺寸和操作条件的变化,为反应器的设计和优化建立可靠的放大准则。但是,CFD 模型准确性尚不可靠,而激光粒子图像速度场仪PIV(Particle Image Velocimetry)测量技术可以准确的获得搅拌槽中丰富的信息,如 :时均或瞬时速度、动能耗散速率、剪切速率等,并可进一步得到宏观特性参数,可以验证CFD 模型的仿真结果和提供模型边界条件。因此,PIV 和CFD 相结合的研究方法对搅拌混合设备的放大和优化研究具有重要的理论意义和应用价值。
1 PIV 测量技术
测量搅拌设备内物料形成的流场是对搅拌流动本质认识的最基本和最关键的一步。早期流速测量方法有皮托管、电磁流速法、压电探头和热线或热膜风速仪等,但插入流场中的探头对流型产生影响,目前已很少使用。随着激光技术的发展,激光多普勒测速仪LDV(Laser Doppler Velocimetry) 和PIV 是 在20 世纪80 年代才发展起来非接触流场测量新技术。LDV 可以测量某一测点的时均速度,但不能获得瞬时速度值,且只能单点测量,实验工作量大。PIV 技术突破了单点测量的缺点,综合了单点测量技术和显示测量技术的优点,既具备单测量技术的精度和分辨率,又具备平面流场显示的整体结构和瞬态图像。其原理是在液体内放入一定量的与液体密度相同的示踪粒子(确保其跟随性良好),在由一狭缝激光束照射,两个脉冲激光源形成的偏光源照射下,由高分辨率的摄像机拍得两次曝光图像,接着从曝光时间内粒子的位移计算出速度场。
搅拌槽中存在三种类型的运动:平均流场(全局流动),周期性波动(尾涡轨迹),瞬时脉动(能量耗散),均可通过PIV 手段测量。PIV 测量技术可以提供瞬态和时均速度场,为分析反应器内的流体流动提供可靠的信息。随着显示测量和处理技术的发展,PIV方法能够通过直接测量的方法计算槽内的湍流动能耗散速率(turbulent energy dissipation,ε)[1]。由于湍流流动耗散发生在非常小的Kolomogorov 尺度,现有的PIV 测量技术很难达到如此高的分辨度,理论上讲PIV 直接测量估算值小于真实值。Sheng 等[2]在2000年提出大涡PIV 方法,对PIV 可分辨的尺度上直接计算脉动,对不可分解的尺度上的脉动用亚格子模型求解,在四斜叶桨搅拌槽内计算ε,得到了很好的结果,与直接测量方法相比大涡PIV 对空间分辨率要求较低。Gabriele 等[3]首次依据能量输入来评价直接测量法、无因次分析法以及大涡PIV 三种方法的优劣,结果表明大涡PIV 方法结果更加合理可靠,但预测结果受亚格子模型常数Cs值影响大,Meneveau 等[4]对Smagorinsky-Lily 模型进行改进,认为应力大小与局部流体应变速率成正比。
目前,对流体流动的研究大多集中在二维平面PIV[5-7],湍流动能耗散速率的计算均是基于各向同性的假设,Khan 等[8]采用双相机PIV 方法测量三维速度,验证了对于具有较好对称性和漩涡不强的流动,平面PIV 方法计算验证了湍流动能的合理性和相对准确性。但对于三维特性很强的流动结构,如高速射流,三维体测量技术必不可少。随着实验技术的发展,三维体PIV 技术(volumetric PIV)得到了长足的发展,其是基于原有的数字式粒子图像测速系统基础之上,利用类似于生物双目视觉原理,使用两套数字式粒子图像测速装置,空间上按照一定倾斜角度同时拍摄实验区域,通过得到的两套二维速度向量场合成计算得到测试区域内的三维速度向量场结果。层析PIV是被用于测量三维瞬时速度的新方法[9],将医学层析扫描采用的倍增代数重构技术(multiplicative algebraic reconstruction technique,MART)[10]应用于三维示踪粒子场重构,成功突破了以往体PIV 测量空间分辨率不够的技术瓶颈,使得体PIV 测量进入真正意义上的使用阶段。
未知变量数大于方程数,要使方程封闭则必须作出假设,需对应力项 建立模型。常用的模型有k-ε(Standard,RNG 和Realizable k-ε 模型),k-ε(Standard 和SST k-ε 模型)及雷诺应力模型(Reynolds Stress Model,RSM)等。RANS 模型因其计算经济,可以获得工程上较为准确的宏观参数,如:流型、功率消耗和排出流量等参数,且容易扩展到多相流[12-13]和化学反应的模拟中,是现在工业研究中应用最广泛的湍流模型。但RANS 方法中各种模型都有一定的局限性,依赖经验数据,对反应器内复杂流动、桨叶区湍流特性[1,14]及尾涡发展[14-16]预测不够准确,这是因为桨叶区和尾涡区高度各向异性,而RANS 则假设各向同性,湍流模型需加以改进才能获得准确结果。
2 CFD 模拟
PIV 可以提供丰富的流动信息,但实验条件苛刻,如要求搅拌槽和流体透明,槽内搅拌桨和部件不反光,限制因素多,且欲获得全槽流动信息,工作量仍较大,无法完全依赖这种方法实现混合设备的优化和放大。近年来利用计算流体力学(computational fluid dynamics,简称CFD)数值模拟方法,可以快速模拟搅拌槽内流动状况及特性参数随几何尺寸和操作条件不同发生的变化。因此,建立合理有效的数值模拟方法,对新型反应器的开发和过程放大开辟了一条新途径,是流体混合技术发展的趋势。
搅拌槽中湍流模拟方法主要有三种:直接数值模拟(DNS),雷诺平均方法(RANS)和大涡模拟方法(LES)。三种方法的关系如图1[11]所示。直接数值模拟DNS 对湍流脉动所有尺度直接求解,最小网格尺度应小于耗散区尺度,但受到计算机水平的限制,目前仅能计算低雷诺数和简单几何条件问题,到解决工程实际问题还有距离。
雷诺平均方法是将非稳态控制对时间作平均的方法对全部尺度进行模拟计算,基本方程如下:
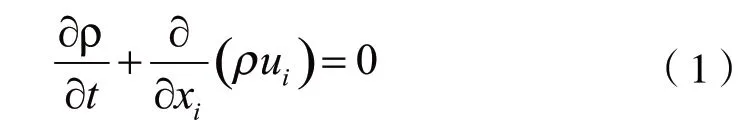
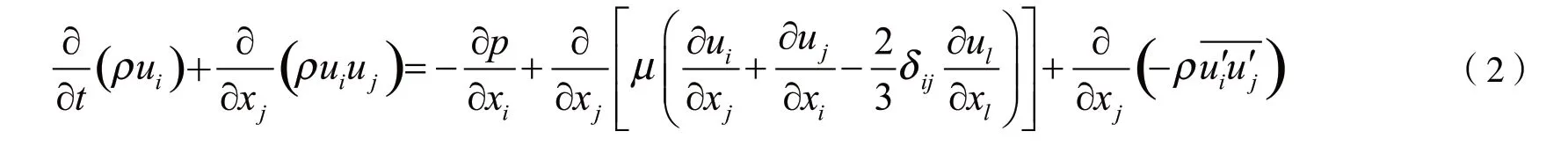
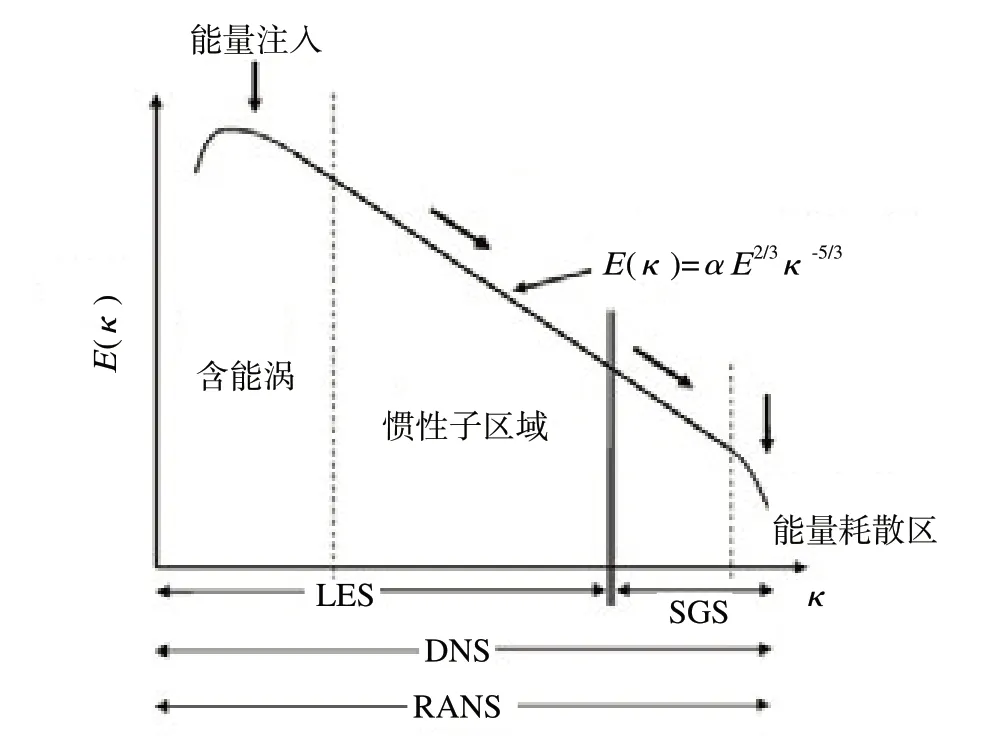
图1 直接数值模拟、雷诺平均方法和大涡模拟方法与漩涡尺度的关系
大涡模拟是介于直接数值模拟和雷诺平均方法之间的折中模型,其基本思想是通过滤波方法把湍流瞬时运动分解成大尺度运动和小尺度运动两部分。大尺度量通过直接求解N-S 方程计算,小尺度量采用亚格子(SGS)模型进行模化。控制方程如下:
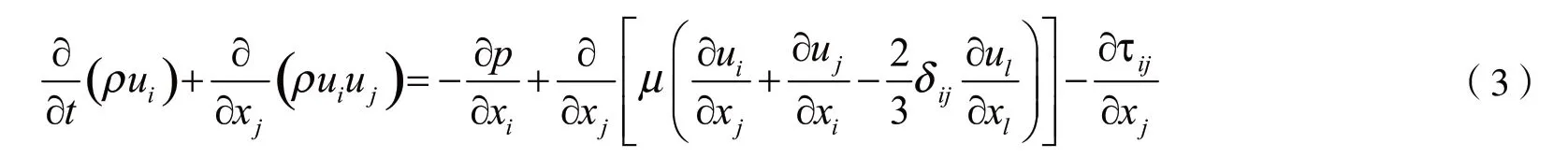
其中,τij由亚格子应力模型求取,一般常用标准Samagorinsky-Lily 模型。大涡计算取决于研究对象的边界条件和几何形状,因而各向异性。小涡不依赖于几何条件,各向同性,具有普遍性,易于寻找一个普适的模型对小涡进行模拟。较RANS 模型,LES 方法要求更加精细的网格,但是可以提供重要的湍动信息。
3 PIV 和CFD 的耦合应用
3.1 速度场
透过微观流动信息能够深入认识流动本质。搅拌桨设计的基础是分析搅拌设备内物料形成什么样的流场,明确在不同搅拌桨的型式、尺寸、离底距离、操作条件等条件下,流场对混合、悬浮和分散等过程的影响。Li 等[17]采用LES 模型对涡轮桨流动特性进行研究,并与PIV 实验和标准k-ε 模型结果进行对比,结果(如图2)表明k-ε 模型模拟的轴向速度和湍流动能与PIV 实验值偏差较大,LES 模型能够更好的预测复杂流动。此外,在模型验证的基础上考察了桨叶直径对流型的影响[17](如图3),当桨叶直径由T/3 增大到T/2 时,单循环会分裂成双循环,因为桨叶直径增大,墙壁对流动的限制作用加强,排出流方向几乎呈水平,出现双循环流型。
搅拌桨末端的尾涡区域内湍动能很高一般超过区域外湍动能一个数量级,对气体分散、液体混合等都产生显著影响。Ranade[19]采用PIV 和CFD 方法研究了气液体系中尾涡结构,PIV 相位分析得到尾涡位置处出现气穴,其原因是尾涡区域湍动能高,而压力远低于区域外压力,气体首先会在低压力区聚集。对于径向流桨,气穴由于受到浮力的作用,只会向上运动,不会分散到下部循环流中。研究桨叶片尾涡结构对控制桨叶剪切分散效率、防止液泛及桨叶设计等都有十分重要的意义[20]。
针对不同的物料系统和搅拌目的,对轴向、径向、切向流动强弱要求是不同的。基于速度场可采用流函数方法[21]进行流量准数的定量化。Iranshahi 等[22]采用数值模拟方法研究了Paravisc 桨、双螺带桨(DHR)和锚式桨三种桨不同方向的流量准数,结果表明,锚式桨轴向泵送能力差,径向和切向的流量高于另外两个桨,双螺带桨切向作用能力最强,三种桨有一个共同点,即切向泵送能力强于轴向,这是高粘流体混合的典型行为特征。
3.2 湍流动能耗散速率
搅拌反应器内湍流动能耗散速率的大小及其分布,直接影响微观混合和反应产物以及多项体系的介观特性,是搅拌反应器内湍流结构的关键参数。相关研究[2,5,7]表明高湍流动能耗散速率受尾涡运动影响,搅拌桨区域湍动是高度异性。蔡清白等[20]通过PIV 实测和LES模拟研究翼型桨叶片尾涡结构与湍动能分布及湍流特性的关系,叶片尾涡内湍动能一般远大于液体主体区,根据湍动能图揭示翼型桨叶片尾涡与桨叶尖为发生脱离,对于气液体系,可有效防止液泛,但也可能引起气体分散不充分。
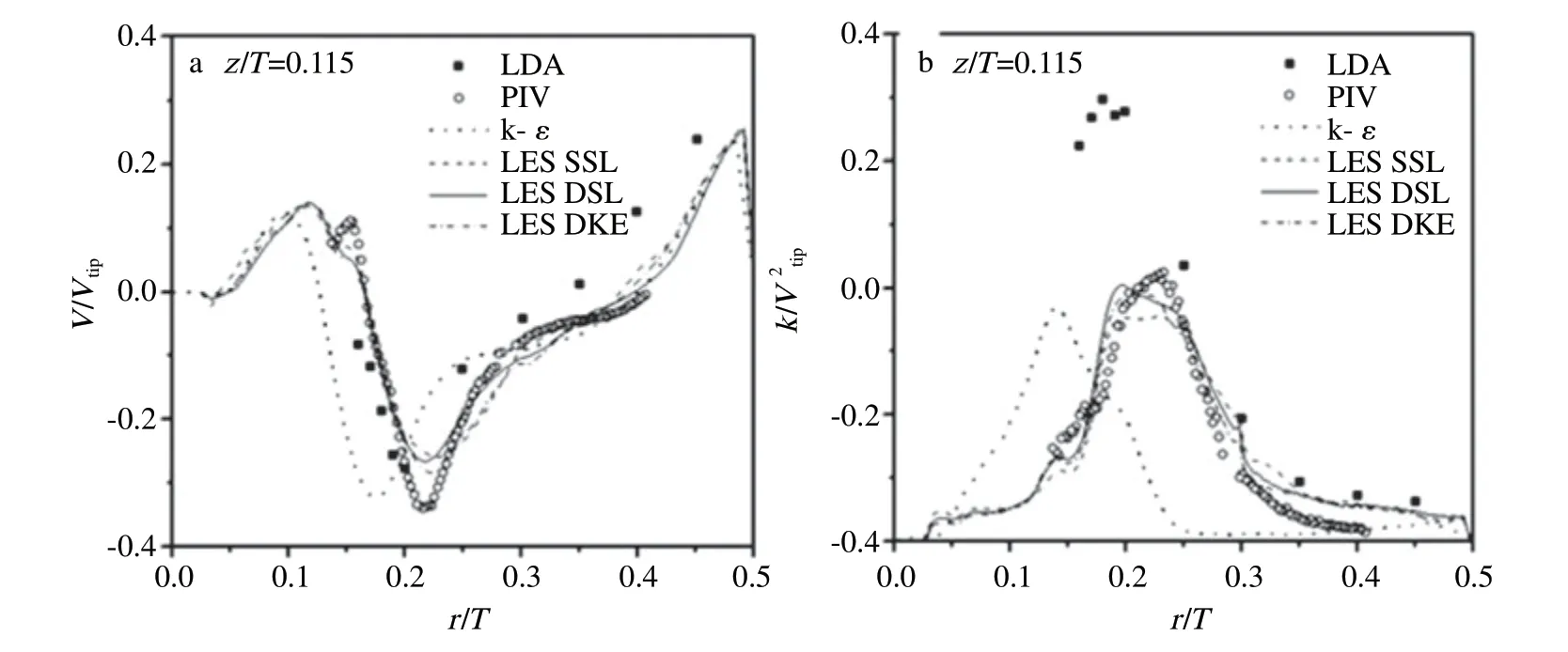
图2 Re=40 000 时轴向速度(a)和湍流动能(b)沿径向分布
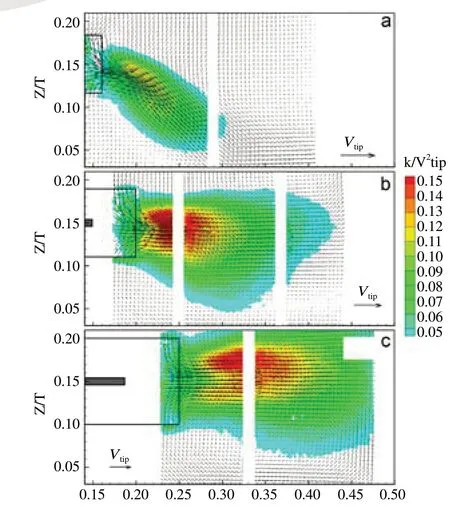
图3 不同直径的涡轮桨流型和湍流动能分布:(a)D/T=0.33,(b)D/T=0.34,(c)D/T=0.5
Ge 等[23]中对标准斜叶桨叶片形状进行优化,通过PIV 实验和CFD 模拟分析改进后斜叶搅拌桨的流动特性,结果表明,将迎液面矩形叶片改变成圆弧状可以减低能量耗散(如图4),增大背液面叶片面积可以增大径向和轴向速度,特别是桨叶附近,并且加强了底部循环能力,这为高效叶片结构的开发提供了指导。
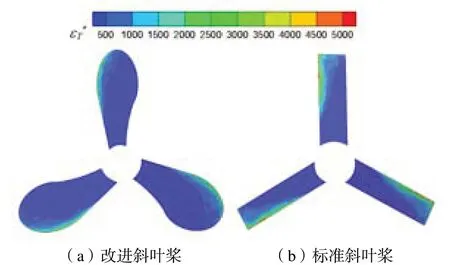
图4 桨叶片位置动能耗散速率分布
根据能量守恒原理[24],可以通过湍流动能速率体积分计算功率消耗,Ankamma 等[25]采用模拟和实验方法对节能涡轮桨功率消耗进行研究,实验结果与模拟结果的偏差小于4%,验证了模拟方法计算功率的准确性。另一方面,V 型桨和矩形桨功率消耗均低于标准的涡轮桨,新型的节能涡轮桨可以用于化工和生物过程中流体的混合与气体分散。
3.3 剪切速率分布
剪切速率是分散混合过程中需要考虑的重要参数。如:气泡的破碎,液滴的形成,粒子沉降等工业应用中,剪切速率分布影响最终产品质量。例如:培养细胞增长过程中,必须严格控制剪切速率大小,准确预测搅拌槽内剪切速率分布及最大值位置,对剪切敏感型流体反应器设计及放大具有重要的知道意义。
相关研究表明[26-27]桨叶表面剪切速率高于槽主体剪切速率几个数量级。此外,剪切速率分布也受挡板结构影响,加入挡板后由于挡板表面存在较大的速度梯度,桨叶与挡板相互作用区域的剪切速率会增大30%[27]。Iranshahi 等[26]发现,与普通的叶片涡轮桨相比,最大叶片桨能够获得相对均匀的剪切速率分布,适用于剪切敏感过程,并且叶轮简单,以及可以在较宽的雷诺数范围内操作,被认为是最具有潜力的新型桨之一。
4 结论
在完善二维PIV 的同时,三维PIV、多相流PIV以及微PIV 等技术是必然的发展趋势,这些研究前景广阔,极大拓展了PIV 的应用范围。CFD 数值模拟方法目前主要集中在雷诺平均方法(RANS)和大涡模拟方法(LES),而直接数值模拟方法由于计算量原因尚难以工程化应用。PIV 实验测量技术和CFD 数值模拟方法可提供搅拌槽内详细的微观流动信息,如:速度场、剪切速率场和动能耗散速率等,并可进一步计算得到宏观参数,如:搅拌功率、循环流量、泵送流量和混合时间等,为搅拌桨设计和优化提供有用指导。随着高性能计算技术的发展,CFD 数值模拟方法将会得到更大的应用,其与先进的三维PIV 技术的耦合,将成为搅拌反应器设计与优化的重要方法。
[1] Delafosse, A.L; Collignon, M.-L.; Crine, M.; Toye, D. Estimation of the turbulent kinetic energy dissipation rate from 2D-PIV measurements in a vessel stirred by an axial Mixel TTP impeller[J]. Chemical Engineering Science, 2011, 66: 1728-1737.
[2] Sheng, J.; Meng, H.; Fox, R.O. A large eddy PIV method for turbulence dissipation rate estimation[J]. Chemical Engineering Science, 2000, 55: 4423-4434.
[3] Gabriele, A.; Nienow, A.W.; Simmons, M.J.H. Use of angle resolved PIV to estimate local specific energy dissipation rates for up- and down-pumping pitched blade agitators in a stirred tank[J]. Chemical Engineering Science, 2009, 64: 126-143.
[4] C., Meneveau; J., Katz. SCALE-INVARIANCE AND TURBULENCE MODELS[J]. Annu. Rev. Fluid Mech, 2000, 32: 1-32.
[5] Escudié, R.; Liné, A. Analysis of turbulence anisotropy in a mixing tank[J]. Chemical Engineering Science, 2006, 61: 2771-2779.
[6] Hlawitschka, M.W.; Bart, H.-J. Determination of local velocity, energy dissipation and phase fraction with LIF- and PIVmeasurement in a Kühniminiplant extraction column[J]. Chemical Engineering Science, 2012, 69: 138-145.
[7] Huchet, F.; Liné, A.; Morchain, J. Evaluation of local kinetic energy dissipation rate in the impeller stream of a Rushton turbine by timeresolved PIV[J]. Chemical Engineering Research and Design, 2009, 87: 369-376.
[8] Khan, F.R.; Rielly, C.D.; Brown, D.A.R. Angle-resolved stereo-PIV measurements close to a down-pumping pitched-blade turbine[J]. Chemical Engineering Science, 2006, 61: 2799-2806.
[9] Elsinga, G. E.; Scarano, F.; Wieneke, B.; Oudheusden, B. W. Tomographic particle image velocimetry[J]. Experiments in Fluids, 2006, 41(6): 933-947.
[10] Debasish, M. K. A robust mart algorithm for tomographic applications[J]. Numer Heat Tr B-Fund, 1999, 35: 485-506.
[11] Joshi, J.B.; Nere, N.K.; Rane, C.V.; Murthy, B. N.; Mathpati, C.S.; Patwardhan, A.W.; Ranade, V.V. CFD simulation of stirred tanks: Comparison of turbulence models (Part II: Axial flow impellers, multiple impellers and multiphase dispersions)[J]. THE CANADIAN JOURNAL OF CHEMICAL ENGINEERING, 2011, 89(4): 754-816.
[12] Qi Nana, Zhang Hu, Zhang Kai, et al. CFD simulation of particle suspension in a stirred tank[J]. Particuology, 2013, 11(3): 317-326.
[13] Murthy, B. N.; Kasundra, R. B.; Joshi, J. B. Hollow self-inducing impellers for gas–liquid–solid dispersion: Experimental and computational study[J]. Chemical Engineering Journal, 2008, 141(1-3): 332-345.
[14] Harminder, S.; David, F.F.; Justin, J.N. An assessment of different turbulence models for predicting flow in a baffled tank stirred with a Rushton turbine[J]. Chemical Engineering Science, 2011, 66: 5976-5988.
[15] Hartmann, H.; Derksen, J. J.; Montavon, C.; Pearson, J.; Hamill, I. S.; van den Akker, H. E. A. Assessment of large eddy and RANS stirred tank simulations by means of LDA[J]. Chemical Engineering Science, 2004, 59(12): 2419-2432.
[16] Murthy, B. N.; Joshi, J. B. Assessment of standard , RSM and LES turbulence models in a baffled stirred vessel agitated by various impeller designs[J]. Chemical Engineering Science, 2008, 63(22): 5468-5495.
[17] Li, Z.P.; Bao, Y.Y.; Gao, Z.M. PIV experiments and large eddy simulations of single-loop flow fields in Rushton turbine stirred tanks[J]. Chemical Engineering Science, 2011, 66: 1219-1231.
[18] Montante, G., Lee, K.C., Brucato, A., Yianneskis, M.. An experimental study of double-to-single-loop transition in stirred vessels. Canadian Journal of Chemical Engineering, 1999, 77: 649–659.
[19] Ranade, V. V.; Perrard, M.; Xuereb, C.; Le Sauze, N.; Bertrand, J. Influence of Gas Flow Rate on the Structure of Trailing Vortices of a Rushton Turbine: PIV Measurements and CFD Simulations[J]. Chemical Engineering Research and Design, 2001, 79(8): 957-964.
[20] 蔡清白; 戴干策. 翼型桨叶片尾涡结构的PIV 实测与LES 模拟研究[J]. 过程工程学报, 2011, 11(4): 541-548.
[21] Heniche, M.; Tanguy, P. A.; Reeder, M. F.; Fasano, J. B. Numerical investigation of blade shape in static mixing[J]. AIChE Journal, 2005, 51(1): 44-58.
[22] Iranshahi, A.; Heniche, M.; Bertrand, F.; Tanguy, P.A. Numerical investigation of the mixing efficiency of the Ekato Paravisc impeller[J]. Chemical Engineering Science, 2006, 61(8): 2609-2617.
[23] Ge, C.Y.; Wang, J.J.; Gu, X.P.; Feng, L.F. CFD simulation and PIV measurement of the flow field generated by modified pitched blade turbine impellers[J]. Chemical Engineering Research and Design, 2013.
[24] Devals, C.; Heniche, M.; Takenaka, K.; Tanguy, P. A. CFD analysis of several design parameters affecting the performance of the Maxblend impeller[J]. Computers & Chemical Engineering, 2008, 32(8): 1831-1841.
[25] Ankamma Rao, D.; Sivashanmugam, P. Experimental and CFD simulation studies on power consumption in mixing using energy saving turbine agitator[J]. Journal of Industrial and Engineering Chemistry, 2010, 16(1): 157-161.
[26] Iranshahi, Arash; Devals, Christophe; Heniche, Mourad; Fradette, Louis; Tanguy, Philippe A.; Takenaka, Katsuhide. Hydrodynamics characterization of the Maxblend impeller[J]. Chemical Engineering Science, 2007, 62(14): 3641-3653.
[27] Wu, J.; Graham, L.J.; M.N., Noui. Estimation of agitator flow shear rate[J]. AIChE Journal, 2006, 52(7): 2323-2332.

