效法伽利略 探索发现之旅

梁继鲁 田 丰 李军伟

（博乐市高级中学 新疆 博乐 833400）

一代科学巨匠伽利略在对运动的研究中创立了一套对近代科学的发展极为有益的科学方法.爱因斯坦曾赞美道：“伽利略的发现以及他所应用的科学的推理方法，是人类思想史上最伟大的成就之一，而且标志着物理学的真正开端.”［1］伽利略在研究自由落体运动时，不迷信权威，大胆探索，采用“发现问题→提出猜想→数学推理→实验验证→合理外推→得出结论”的模式，取得了很大的成功，“两个铁球同时落地”的故事广为流传.

作为一名高中物理教师，在向学生传授知识的同时，必须重视物理规律的建立过程，了解、学习和掌握科学家的科学的研究方法，提高学生的科学素养.这正是“新课改”所大力倡导的，也是我们在教学实践中要身体力行的.

对于物理规律的教学，许多专业书上都有论述.“教无定法”！在教学实践中，对同一教学内容，不同的教师针对不同的教学对象有不同的处理教材的方法.但有的教师对于物理规律的教学干脆采取“不要问它从哪里来”，会用公式解题就行的态度，只重视物理规律的应用，着重培养学生的解题能力，而对于物理学科所特有的科学方法论的教学却被忽略.有的年轻教师把学生会做题作为终极目标，其教学过程是：第一步直接给出规律、公式，第二步就是大运动量训练，采用题海战术.这样做可以培养解题高手，但却不能很好地培养学生的思维能力和科学品格，与“新课改”精神背道而驰！“题海战术”使学生负重如牛.

物理规律的教学中，我们既要让学生掌握物理规律，更要让学生知道其来龙去脉，掌握物理问题的研究方法以及物理规律的形成过程.既要授学生以“鱼”，又要授学生以“渔”.具体来说，物理规律的教学应注意以下两点：

一是让学生明确建立某一物理规律的目的和具体方法，使学生主动地参与建立物理规律的全过程的探究，这点对学生掌握物理的思维方法有重要的感性意义；

二是要让学生了解建立物理规律的主要环节.这个主要环节有：过程的分析，模型的选取，忽略的因素，规律的形成等等.学生对这些主要环节的思考，能增加学生对物理研究方法的感性认识.

在这个过程中培养起来的思维能力，与运用规律解题所培养的思维能力有相当的不同.不重视建立规律的环节，只侧重于运用规律解各种难题，是片面培养学生思维能力的做法，是造成当前一些学生“高分低能”状况的主要原因［2］.

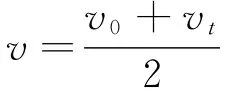
这节内容的教学之所以难，就在于刚进入高中的学生娃没有相关的数学知识（如数列、极限、特别是“微积分”的思想）作支撑.针对本节内容的特点我们决定效法伽利略，探索发现之旅.基本模式是：发现问题→提出猜想→数学推理→实验验证（误差分析）→合理外推→得出结论（建立物理规律）.在讨论中发挥计算机的绘图及计算功能，运用多媒体课件辅助教学，收到了比较好的效果.下面具体谈谈这节内容我们的教学基本过程.

1 发现问题

刚进入高一的学生，他们的思维特点还是经验型的，需要用具体的数据作为他们推理过程的支撑.在具体教学实施过程中，我们由特殊到一般，从讨论一个具体问题入手.通过对具体数据和具体图像的分析来突破教学难点，帮助学生实现从感性思维到理性思维的飞跃.

在复习匀速直线运动的位移公式以及vt 图像所围矩形面积能表示位移等知识点后，接着讨论一个求匀变速直线运动位移的具体问题：

问题：作匀加速直线的物体初速度v0＝10 m／s，加速度a＝2m／s2，如何运用已有的知识计算出物体在15s内位移x？（位移x 已由精密仪器测得为375m）.

分析：速度“不变”问题中的位移的计算学生已能解决，而这个问题中速度是“变化”的，那么位移应如何求出呢？

2 提出猜想

面对所发现的问题应该如何解决，我们引导学生大胆提出猜测：对于匀速直线运动，v－t 图像所围的面积为矩形，这个面积可以表示这段时间的位移；那么：对于匀变速直线运动，v－t 图像所围的面积为梯形，这个梯形面积是不是也可以表示这段时间的位移？

3 数学推理

这里提出的猜想是否正确需要通过科学分析、推理进行验证，这正是本节教学难点所在！我们要重视引导学生从已知探究未知的探索过程.在这里就是辩证地看待物理问题中的“变”与“不变”的关系.在匀变速直线运动整个过程中速度是变化的，而在微小的时间间隔中，速度的变化量就是微小量（即速度的变化量为“可忽略因素”），可以视为不变，这样就将速度“变化”的问题转化为速度“不变”的问题来近似处理，用已经学过的匀速直线运动的知识即可算得位移的近似值.问题中直接给出位移的精确值是为后面误差分析提供参考点，分析这样处理所产生的绝对误差和相对误差.

在下面的具体讨论过程中，我们按照教科书上的安排逐步展开：将所给问题中的匀变速直线运动的时间分成N 等份，在每一份时间Δt 中将速度变化的过程近似作为速度不变来处理，算出位移的近似值，然后将每个Δt内的小位移近似值加以累加得出整个过程位移的近似值；同时运行多媒体课件，绘出在v－t图像中得到由N 个矩形所组成的阶梯形，阶梯形所围的面积可以表示这段时间t内物体总位移的近似值.将N 的取值从小到大，分析所产生的误差的大小随N 的增大时的变化趋势，通过分析推理、合理外推得出结论.为了加深学生的感性认识，教师指导学生亲自动手分别计算N ＝3；N ＝5；N ＝15时位移的近似值，并运用多媒体课件进行绘图和验算（N ＝3；N ＝5；N ＝15是为了方便学生计算），并将结果记下便于后面进行分析.

（1）将问题中总时间15s分成3等份，将每等份时间（5s）内速度变化问题近似作为速度不变问题，算出总位移的近似值为300 m.进一步算出绝对误差为75m，相对误差为20%，运用电脑画出阶梯形并算出相关数据（如图1）；

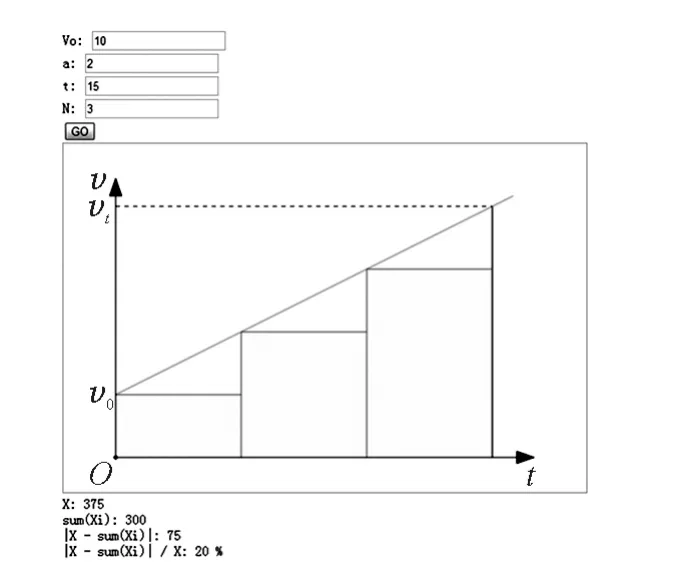
图1

（2）将总时间分成5等份，（每等份的时间为3 s），将每等份时间（3s）内速度变化问题近似作为速度不变问题，算出总位移的近似值为330m，绝对误差为45m，相对误差为12%，电脑画出阶梯形并算出相关数据（如图2）；

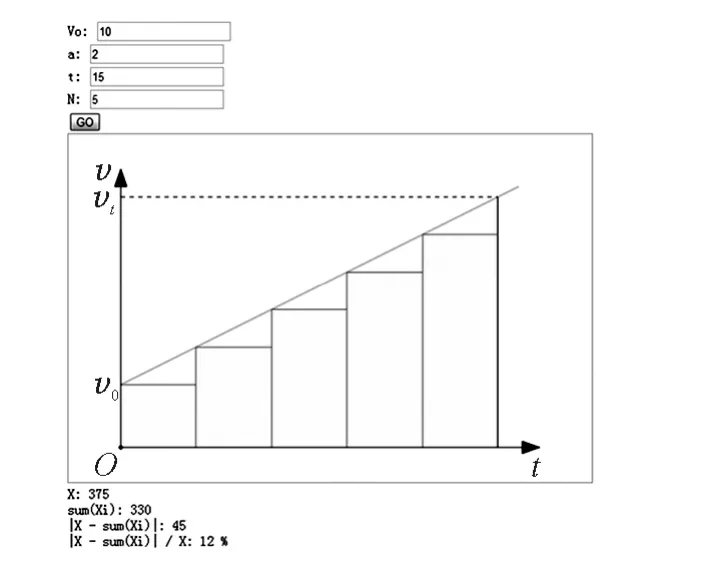
图2

（3）将总时间分成15 等份，（每等份时间为1 s），将每等份时间（1s）内速度变化问题近似作为速度不变问题，算出总位移的近似值为360m，绝对误差为15m，相对误差为4%，电脑画出阶梯形并算出相关数据（如图3）；

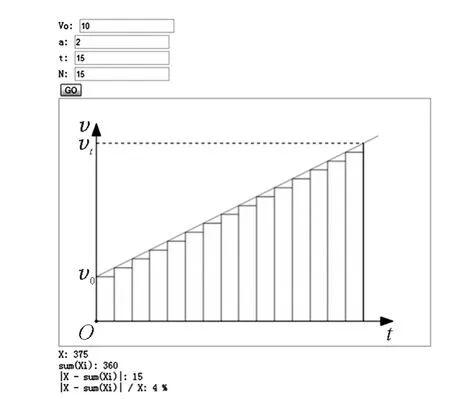
图3

（4）告诉学生运用数学工具（等差数列前N 项和 公式）可算得将总时间1 5 0等份（每等份 时 间0.1s）时，位移的近似值为：373.5 m，绝对误差为1.5m，相对误差为0.4%；将总时间1 500等份（每等份时间0.01s）时，位移的近似值为374.85m，绝对误差为0.15m，相对误差为0.04%.电脑运行多媒体课件绘出N 为150及1 500时的阶梯型图像及计算数据分别如图4（a）和（b）所示.

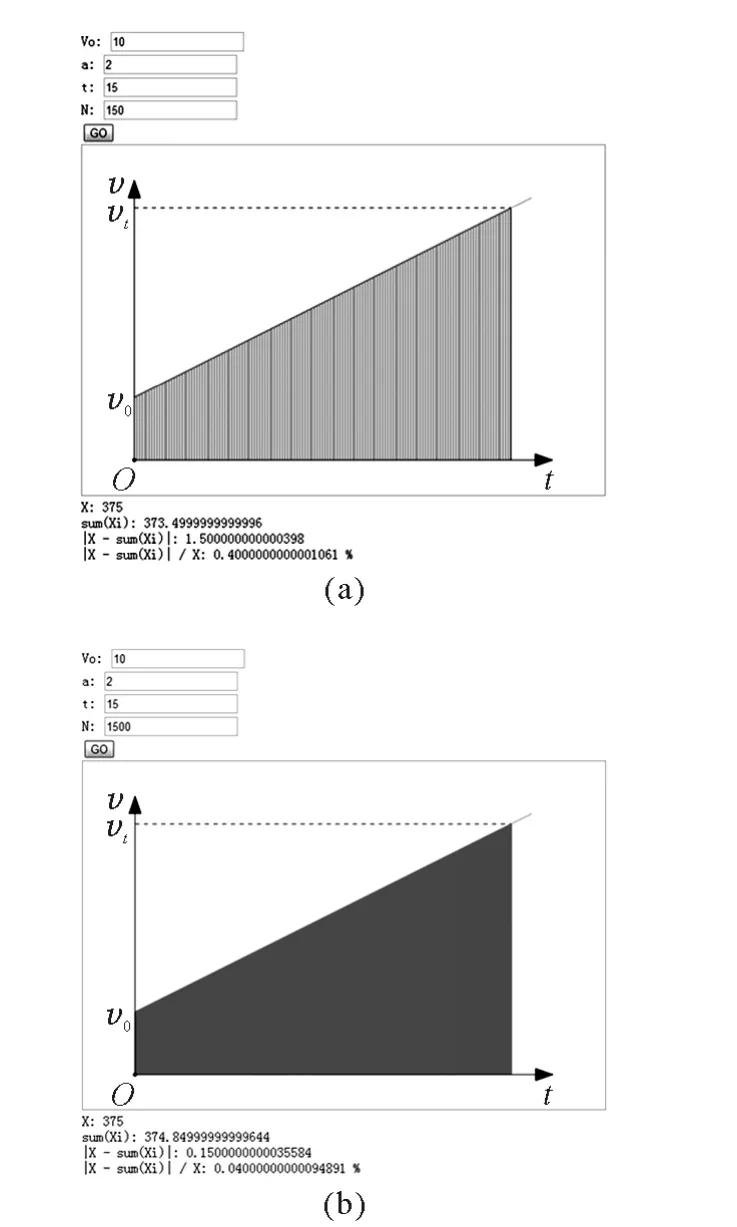
图4

4 误差分析

将上面的计算数据列入表1.

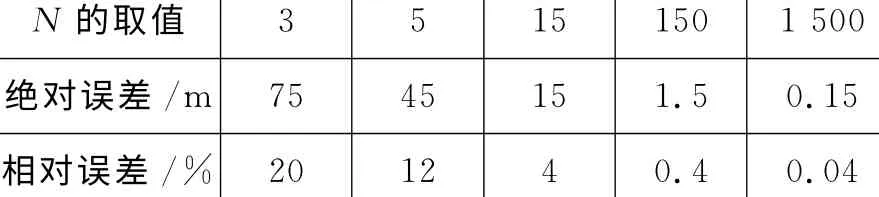
表1

通过分析上面表格的数据及对比5 个图像可知：将时间t等分的份数越多，时间间隔Δt就越小，在Δt内速度的变化就越小，物体在Δt 内的运动就越接近匀速直线运动，用匀速运动替代匀变速运动就越精确；同时图像所围的阶梯形面积越逼近梯形的面积，当N ＝150时，电脑画出的阶梯型就已经看不出是阶梯型，只能看出是梯型了.

5 合理外推

由上面的讨论可以看出：N 取值越大，算得的位移的近似值越接近真实值，阶梯型面积越接近梯形面积.由此可以合理外推：当N 充分大时，计算出的位移的近似值就充分逼近位移的真实值；与此相对应：阶梯型面积充分逼近梯形面积！

6 得出结论

由前面的讨论我们最后可得出结论：

物体做匀变速直线运动时，在v－t 图像中图线所围的梯形面积的数值可以精确表示位移的大小.

根据上面得出的结论，学生自己很快得出匀变速直线运动的位移与时间的关系式.

7 结束语

在物理规律的教学中，教师一定要引导学生弄清规律是如何建立的.有些物理规律是在已有知识的基础上通过分析、推理得出结论，我们就可采用“理论探究法”.本节课的主要难点是让学生正确认识“变”与“不变”的辨证关系，理解在匀变速直线运动中物体的位移对应着v－t 图像所围的梯形面积.解决难点的基本方法是“微元法”，即“分小取近似，求和取极限”的方法（这正是数学分析中的“微积分”的思想）.如果学生能够得出这个结论，那就很好地突破了本节的教学难点！

恩格斯指出：“一个民族要站在科学的最高峰，就一刻也不能没有理论的思维.”伽利略、牛顿、爱因斯坦等等这些伟人，他们的理论思维是我们的指路明灯.我们作为物理教师在教育学生时，要向他们传授科学知识，更要让他们了解那些科学巨人的科学研究方法.让他们象伟人那样去思索、探究.

1 普通高中课程标准实验教科书.物理·必修1.北京：人民教育出版社，2010.49

2 乔际平，续佩君.物理教育学.南昌：江西教育出版社，1992.138