土层性质对钻孔灌注桩孔径变化的影响
沈丽丽,黎 玮
(1.浙江金筑交通建设有限公司,杭州 310051;2.湖州市城市规划设计研究院,浙江 湖州 313000)
土层性质对钻孔灌注桩孔径变化的影响
沈丽丽1,黎 玮2
(1.浙江金筑交通建设有限公司,杭州 310051;2.湖州市城市规划设计研究院,浙江 湖州 313000)
考虑了基于土体随机场理论的土的相关距离,去除取样子样相互不独立的影响,对钻孔灌注桩实测成孔曲线进行了统计分析。采用Grubbs方法去除异常点的影响,并根据随机场理论求出均值和均值方差。最后根据K-S拟合分布检验法进行了分布检验,并对以上过程所得结果进行了分析讨论。
钻孔灌注桩;孔径; 变异性
0 引 言
孔径变异因素是分析钻孔灌注桩竖向承载力的不可忽视的因素,在一定情况下可能会成为主要的影响因素。在不同的土层中,桩孔径的变异特性是不同的,这与土的物理力学性能有关,同时也与施工工艺有密切的关系。在此前的研究中,比较多的学者把目光集中在施工成孔因素对其竖向承载力的影响,能够对钻孔灌注桩竖向承载力造成影响的成孔因素主要体现在孔壁粗糙度、孔壁泥皮、孔底沉渣、成孔时间等方面。
对钻孔灌注桩竖向承载力分析比预制桩更加困难,主要是因为很难定量的估计施工因素对承载力的影响,而这种影响往往会造成难以预料的结果,同类桩基础的竖向承载力会相差一倍左右。综上所分析的一系列施工因素,最终也很大程度上表现在桩身尺寸的不确定性,而桩身尺寸的不确定性又集中表现在桩径的变异。在诸多不确定性因素的影响下,桩径的变异性是不可忽略的。虽然这些施工因素的不确定性很难定量估计,但是当把土层因素的影响考虑在内时,我们可以发现,在同一土层,施工工法、施工条件相同的情况下,孔径的变异是有其分布规律的,因此其孔壁粗糙度、泥皮厚度、沉渣厚度也是有一定规律可循的。
钻孔灌注桩孔径的变异性不仅受地质情况、钻孔深度的影响,还与施工方法、施工设备等因素相关,不同的钻机类型会影响成孔的粗糙度和灌注桩的承载性状,当采用正循环方式成孔时,GPS-10型钻机成孔的孔径大易坍孔,GPS-15型钻机的稳定性好,孔壁成锯齿桩,有利于侧摩阻力的发挥;采用反循环成孔,孔壁较光滑,对于以摩擦桩和端承摩擦桩为主的地区,不利于承载力的发挥;但由于泥浆正循环的特点,泥浆比重、粘度的增加会使泥皮加厚,平均孔径、孔壁平均粗糙度都会减小,泥浆比重、粘度的增加对深部土层的影响比对上部土层影响大。施工时,在能保证清孔质量和孔壁稳定的情况下,尽量减小泥浆的比重和粘度。随着钻头直径的增大,孔径的扩大值会减小,中下部的土层的孔径扩大值小于上部土层,这一现象在选取钻头直径时应引起足够重视,确保孔径大小满足设计要求。本文将收集到的某住宅工程的实际测孔数据(共688根钻孔灌注桩)进行统计分析,以求得到孔径变异性。
1 孔径变异性的统计方法
1.1 异常点去除
目前常用的剔除异常数据的方法主要有三倍标准差判别法(又称拉依达/Pauta准则)、小概率时间判别法(又称肖维耐/Chauvenet准则)、端值判别法(又称格拉布斯/Grubbs方法)、t检验准则法以及非参数方法(又称狄可逊/Dixon方法)等。以往的研究表明,Grubbs方法的检验效果较好且与其他各个检验方法的一致性最佳。
Grubbs先后于1952、1969年发表这一方法,设测定值是正态分布X=N(μ,σ),X的随机子样为x1,x2,……,xn。现按照子样的测试数据由小到大排列如下:
x1,x2,……,xn
设x1,xn,为过小、过大的数值,即可怀疑的异常数据,则可按Grubbs方法判定异常数据。
(1)计算舍弃值得临界值T



(2)选定危险率α
当按照Grubbs方法造成错判时,其错判的危险率为α。一般常用的α为5%或1%。其概率意义是,当测试数据在服从正态分布的条件下,

(1)
(3)异常数据判定
当Ti≥T(n,α),则相应的xi是可怀疑的异常数据,应从子样数据中剔除;反之,当Ti (4)多个异常数据的情况 在一个子样(一组数据)中存在多于一个的异常数据时,应依测定值与平均值的差值,按大小顺序逐个判定、剔除,直到不再有异常数据。 1.2 相关距离的确定 高大钊(1996) 通过对不同土性参数求得的相关距离的比较,指出对于同一土层来说,不同土性参数之间具有十分接近的相关距离值。因此,可以应用前人通过静力触探比贯入阻力曲线求得的相关距离,进行其他指标空间均值方差的计算,这里同样可以应用其进行孔径数据指标的计算,如表1所示。 表1 典型土层相关距离计算表 1.3 孔径统计方法 (1)对一根桩成孔实测数据的统计 (2)对一个场地桩基成孔实测数据的统计 1.4 拟合优度检验 在大样本容量时,一般来说χ2(Chi_Square)法、K_S(Kolmogorov_Smirnov)法、K(Kuiper)法、C_M(Cramer_Von Mises)法、W(Watson)法、S(Shcrman)法、A_D法等检验方法得到的最优分布是一致的,本文采用K_S法来进行拟合优度检验。 K_S检验法取统计量: D+=max(1≤i≤n)[i/n-F(xi)] (2) (3) D=max(D+,D-) (4) 当D 综上所述,采用Grubbs方法进行异常点去除,根据相关距离进行取样,依照上述方法进行统计参数确定,并用K_S法进行拟合分布检验,最终得到如下表2所示结果。 表2 某住宅工程各场地实测成孔数据统计结果 从表2中可以看到,随着土层的不同,埋深不断加深,钻孔灌注桩的平均孔径、孔径标准差、变异系数都有变化,并且都在逐步减小。图1~图3为6个场地的孔径统计情况。 图1 各场地不同土层中平均孔径 图2 各场地不同土层中孔径标准差 图3 各场地不同土层中孔径变异系数 结合已有的研究经验,浅层土层一般为填土及淤泥质粉质粘土。这些土层的形成历史时期较短,固结不充分,土层稳定性较差。且由于浅部土层受施工和地面等扰动较严重,因此这一部分土层中,钻孔灌注桩成孔孔径表现出不规律、离散型较大。由于孔壁土的不稳定,局部小范围孔壁塌陷的发生导致了这一部分土层中平均孔径超出设计值5%~10%。但由于这部分埋深较浅,对钻孔灌注桩侧摩阻力的影响不大。 对于同一土层,钻头直径越小,孔径的扩大值越大。其原因是采用小直径的钻头稳定性差,大直径钻头受到的孔底和侧面压力大,钻进速度随土深和孔径的变大而减慢,钻进越平稳,对土层扰动越小。而同一直径钻头对不同土层的比较来看,随着土层的加深,孔径的扩大随之减小。 从图中,我们还可以看出,随着土层埋深的不断加深,孔径数据的标准差和变异系数不断减小,表明孔径随着土层埋深加深逐步趋于稳定。孔径平均值也随之减小,最终稳定在820mm左右,表明深层土受施工及地面扰动因素影响较小,孔径趋于稳定。 (1)钻孔灌注桩的孔径随着土层埋深的加深,平均孔径和变异性都逐步缩小,并趋于稳定。 (2)浅部土层的孔径表现出不规律、离散型较大。由于受地面影响较大,孔壁土的不稳定,局部小范围孔壁塌陷的发生导致了这一部分土层中平均孔径超出设计值5%~10%。但由于这部分埋深较浅,对钻孔灌注桩侧摩阻力的影响不大。 (3)各层土中孔径的分布均服从正态分布。 (4)以此为基础,可以进一步进行钻孔灌注桩考虑孔径影响的竖向承载力的可靠度分析,得到孔径对可靠度的影响。 [1]薛金贤.钻孔灌注桩孔径变化规律研究[D].上海:上海同济大学,2007. [2]楼晓明,戴仁厚,张一鸣.孔壁形状对钻孔灌注桩承载特性的影响[J].工程勘察,1998,(2):6-9. [3]高大钊.岩土工程设计安全度指标及其应用[J].工程勘察,1996,(1):1-6. [4]朱登峰,高大钊.土性平稳随机场的空间统计特性分析[J].岩土力学,2003,24(3):455-457. 收稿日期:2013-11-22 Research on Impact of Soil Conditions on the Variation of Pile Diameter of Bored Pile SHEN Li-li1,LI Wei2 (1.Zhejiang Golden Construction Traffic Construction Co., Ltd, Hangzhou 310051,China;2.Huzhou Urban Planning and Design Research Institue,Huzhou 313000,China) Based on the random field theory of soil, the coherence distance is taken into consideration to eliminate the influence from the mutual dependence among the samples. The measured values of bored pile diameter are analyzed. Grubbs method is employed to delete the exceptional data points and the mean and the deviation of the data is got through the random field theory. Finally, K-S method is used to survey the distribution of the data and some further analysis is made based on the process. bored pile; pile diameter;variability 2014-01-17 沈丽丽(1982-),女,浙江萧山人,工程师,E-mail:slllfp@126.com。 TU473.14 A 10.3969/j.issn.1671-234X.2014.01.003 1671-234X(2014)01-0010-05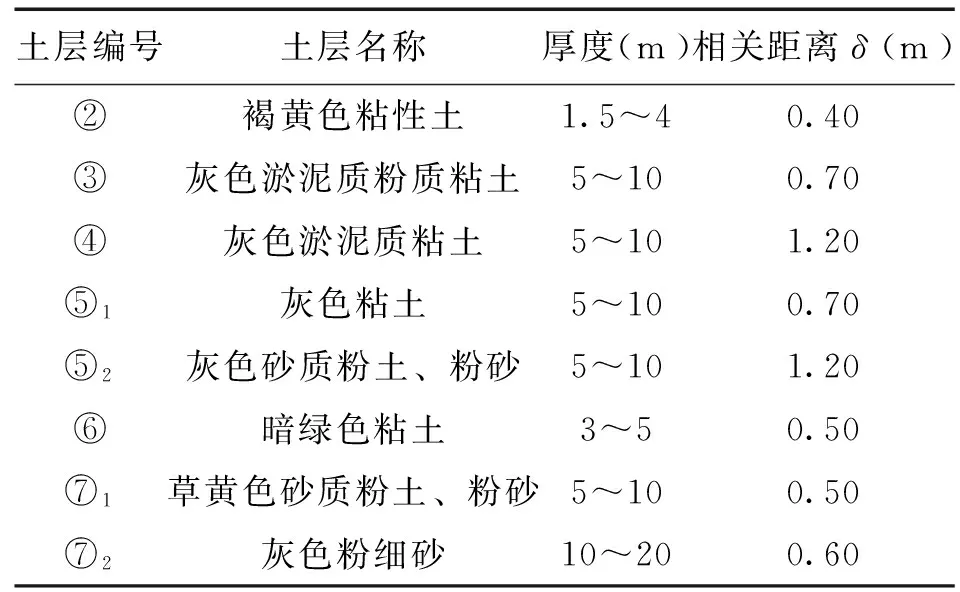



2 孔径变异性的统计规律

3 孔径变异性的分析
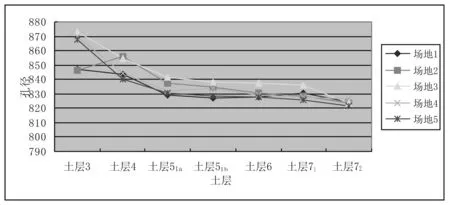
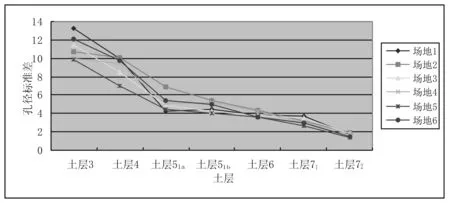

4 结 语

