基于CFD的螺旋溜槽流场及颗粒运动行为数值模拟
高淑玲 魏德洲 崔宝玉 沈岩柏 黄秀挺
(东北大学资源与土木工程学院,辽宁 沈阳 110819)
基于CFD的螺旋溜槽流场及颗粒运动行为数值模拟
高淑玲 魏德洲 崔宝玉 沈岩柏 黄秀挺
(东北大学资源与土木工程学院,辽宁 沈阳 110819)
为了探明螺旋溜槽的流场特征及不同矿物颗粒分选时的行为规律,基于CFD理论,采用k-ε湍流模型、VOF多相流模型和离散相耦合等方法,对直径为300 mm的螺旋溜槽进行流场和颗粒运动行为的数值模拟,进而探讨了螺距和给矿流量对它们的影响。结果表明,螺旋溜槽流场中的水相流速呈明显的条带状分布,其速度值沿槽深方向逐渐升高,沿径向从内向外逐渐增大;湍动能在径向上以类似于椭圆环状分布,外缘的紊流度从上至下逐渐升高;在相同的流场条件下,颗粒运动速度极值与密度大小呈负相关;螺距增大后,水层厚度不变,而水相流速和湍动能相应增加,颗粒的运动速度也明显增加,这有利于加速粒群的分带和分选;给矿流量对水层厚度、流速和湍动能的大小均具有明显影响,但对流场分布特征影响较小,而颗粒运动的随机性与该因素呈正相关,即流量增大会导致粒群分带延迟,影响分选。
螺旋溜槽流场 颗粒运动 CFD 数值模拟 螺距 给矿流量
作为离心力与重力复合力场的典型重选设备,螺旋溜槽因其结构简单、占地面积少、安装与操作简易、分矿清楚、运转可靠等特点[1]在有色金属和铁矿选矿实践中得到了广泛应用[2-4]。为了适应矿石性质、提高设备的处理能力和分选精度,螺旋溜槽不断涌现新的结构和形式,如旋转螺旋溜槽、锲形刻槽螺旋溜槽、多段螺旋溜槽、磁力螺旋溜槽等[5-7],这些新型设备在提高分选技术指标方面各具优势。
螺旋溜槽的分选原理为,矿物颗粒在螺旋溜槽所提供的回转流场中,基于离心惯性力和重力的联合作用做复杂的三维运动,并根据运动差异实现分离。分离的内因是颗粒的物理性质差异,而外因则在于分选空间内的流场特征。随着计算机技术和数值算法的发展,采用计算流体力学(computational fluid dynamics,简称CFD)方法对分选流场进行数值模拟的研究范围不断拓展,如分级、浓缩、重介质分选、跳汰分选、浮选等[8-12]。值得注意的是,围绕离心力和重力复合力场的数值模拟,近年来的研究热点主要集中在旋流器上,而有关螺旋溜槽的模拟研究则相对不足。
本研究基于CFD原理和方法,采用k-ε湍流模型和VOF多相流模型对螺旋溜槽流场进行数值模拟,在此基础上采用离散相耦合方法,进一步对颗粒在螺旋溜槽流场中的运动行为进行模拟研究,并着重探讨了螺距和给矿流量对流场及颗粒运动行为的影响。
1 数值模拟的条件
1.1 数值模拟模型
CFD软件-Fluent是基于有限体积法、用于解决或计算流体流动和传热问题的程序。CFD软件-Fluent提供了多种湍流模型,其中的标准k-ε模型,对于壁面流动及在零或者小于平均压力梯度情况下获得的模拟结果与实验结果吻合,而且在工程上较为常用,所以选用标准k-ε模型进行模拟。此外,由于螺旋溜槽为开放的薄膜流体系,空气的影响不能忽略,因此本研究采用VOF多相流模型对水层的铺展过程进行计算。固相颗粒采用基于拉格朗日法的离散相模型(Discrete Phase Model,DPM),它适用于固相浓度较低的多相流,可以准确地跟踪每一个颗粒的运动轨迹。
1.2 数值模拟的几何模型和边界条件
应用Fluent集成软件中的DM模块创建螺旋溜槽几何模型,利用AM模块进行网格划分。其中螺旋溜槽横断面形状为立方抛物线,螺旋直径为300 mm,圈数为5圈,螺距分别设为120,180,240 mm。螺距为120 mm时的几何模型及网格划分图如图1。

图1 螺旋溜槽几何模型及网格划分
模拟的边界条件设置如下:
(1)流量入口:分别设为3个条件,即5,10,15 L/min。
(2)压强出口:出口相对压强设置为0,并定义空气的回流系数为1。
(3)下底面及侧壁:施加无滑移边界条件。
(4)上表面:设为自由滑移表面。
另外,水和空气分别设置为首相和次相。初始化时,设置整个流体域内充满空气,即在t=0时刻,空气的体积分数为1。
2 数值模拟结果与分析
2.1 螺旋溜槽的流场特征及其影响因素
2.1.1 螺旋溜槽的流场特征
以螺距为120 mm、给矿流量为5 L/min对螺旋溜槽流场进行数值模拟。截取螺旋溜槽轴向面及螺旋半数圈和整数圈标高处的径向水平面,上述截面上的流速和湍动能的分布特征分别如图2、图3。
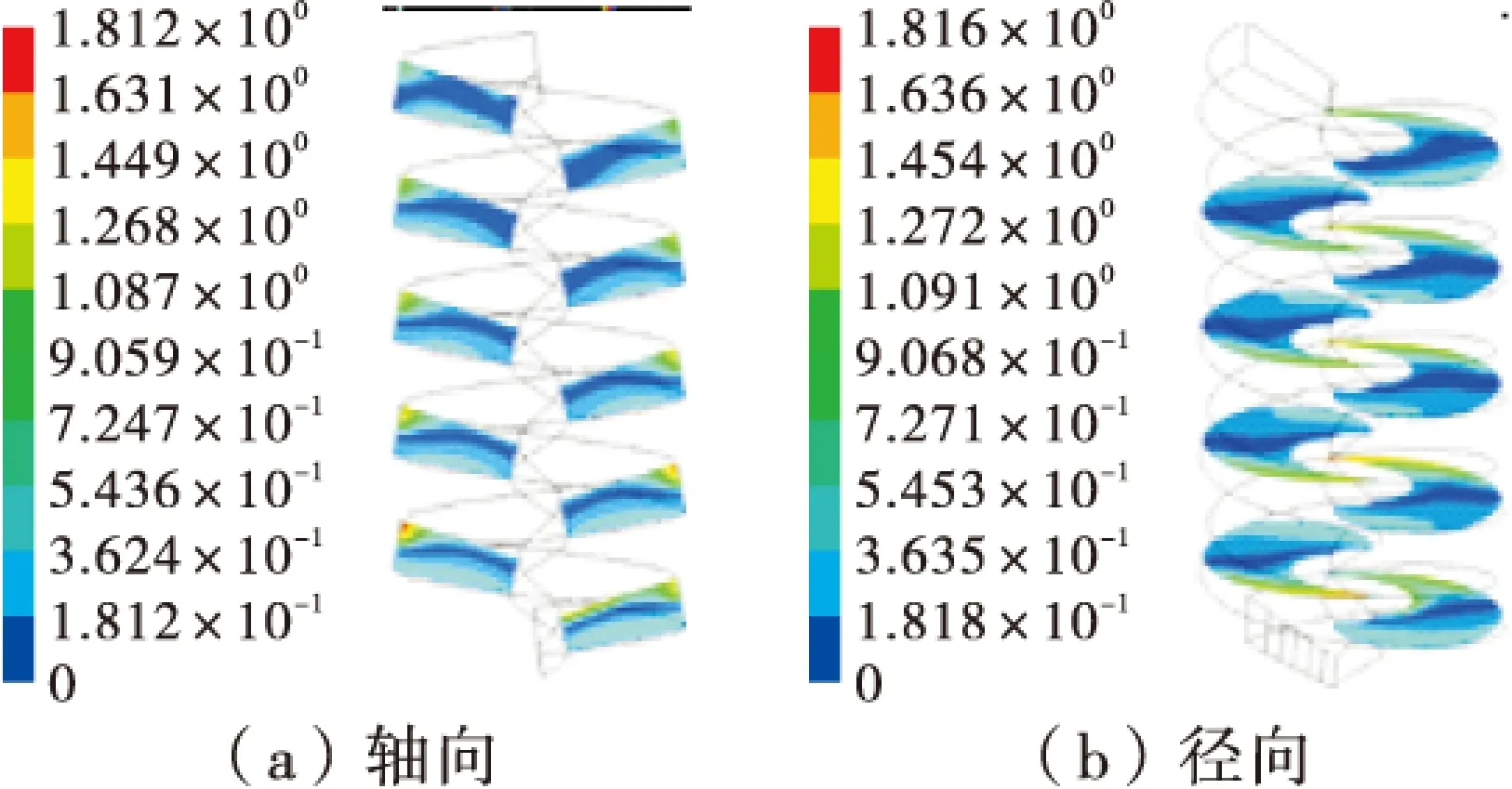
图2 速度分布特征(单位:m/s)
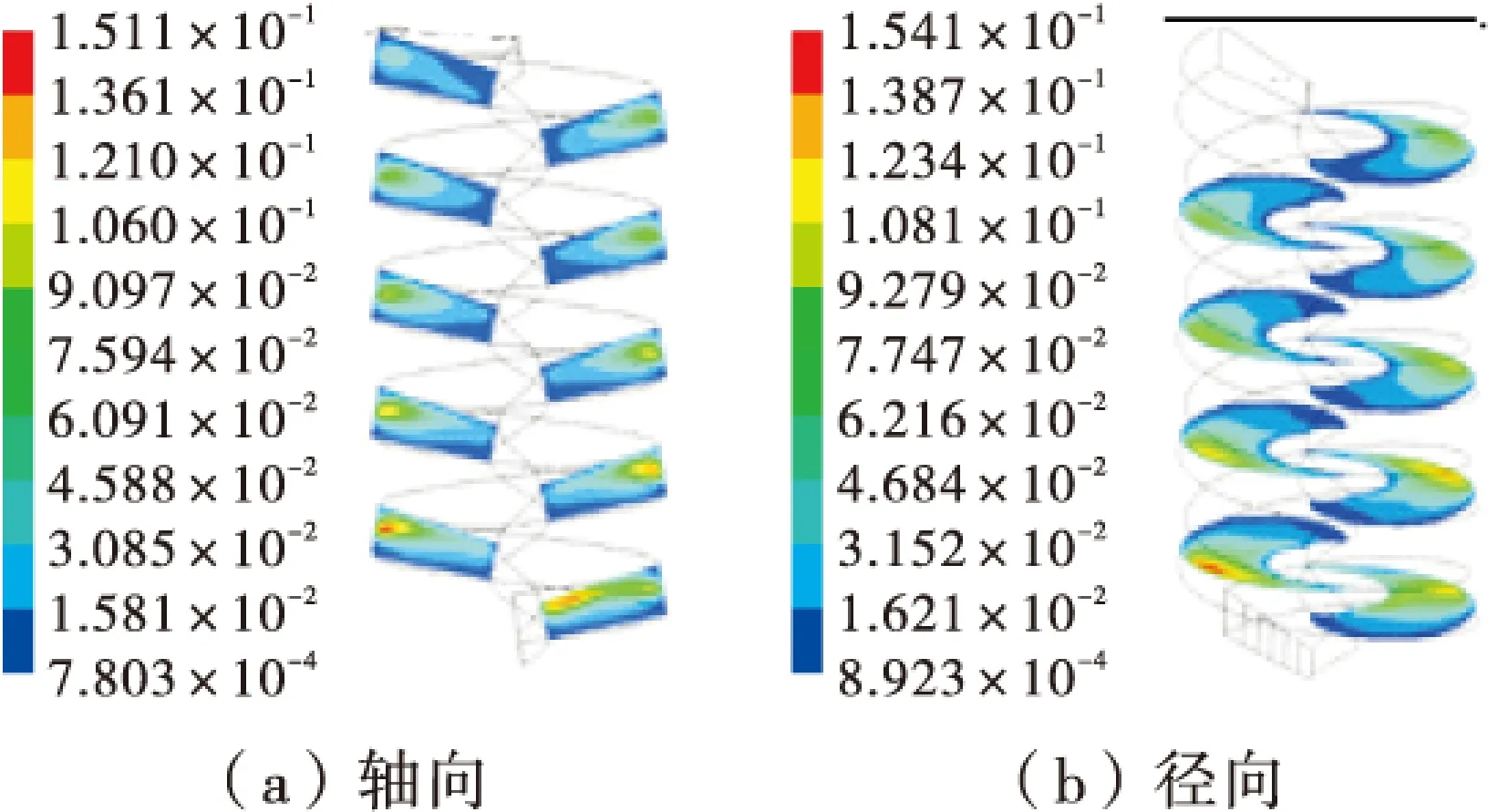
图3 湍动能分布特征(单位:J/kg)
从图2可以看出,在每一个轴向截面上都存在一个速度极小值区域(深色带,最低流速为零),该区域以下的流速沿槽深方向逐渐升高,而其上的流速则沿槽深缓慢降低。根据螺旋溜槽内水流速度的分布特点[13]判断,这些速度极小值区域即为气相与水相的交界面,可将其下边缘视为水层的上表面。水速等值线沿槽底曲面呈条带状分布,这一现象从第三圈开始更为显著,到第五圈时,槽底液流等速线相对变宽。在径向水平面上,速度等值线同样呈条带状,且沿径向垂直方向从内向外逐渐增大。
从图3可以看出,湍动能在径向上以类似于椭圆环状分布,外缘的紊流度从上至下逐渐升高。从轴向上看,空气相受涡流的影响较大,而紧贴着槽底的水流受其影响较小。这说明模拟采用的槽高参数满足计算要求,虽然顶面采用了自由滑移边界,但对实际水相的铺展以及后续选别效果影响不大。
2.1.2 螺旋溜槽的影响因素
2.1.2.1 螺距的影响
仅将2.1.1节的螺距调整为180 mm和240 mm,轴向面上的流场分布特征分别见图4、图5。

图4 螺距为180 mm时的流场特征
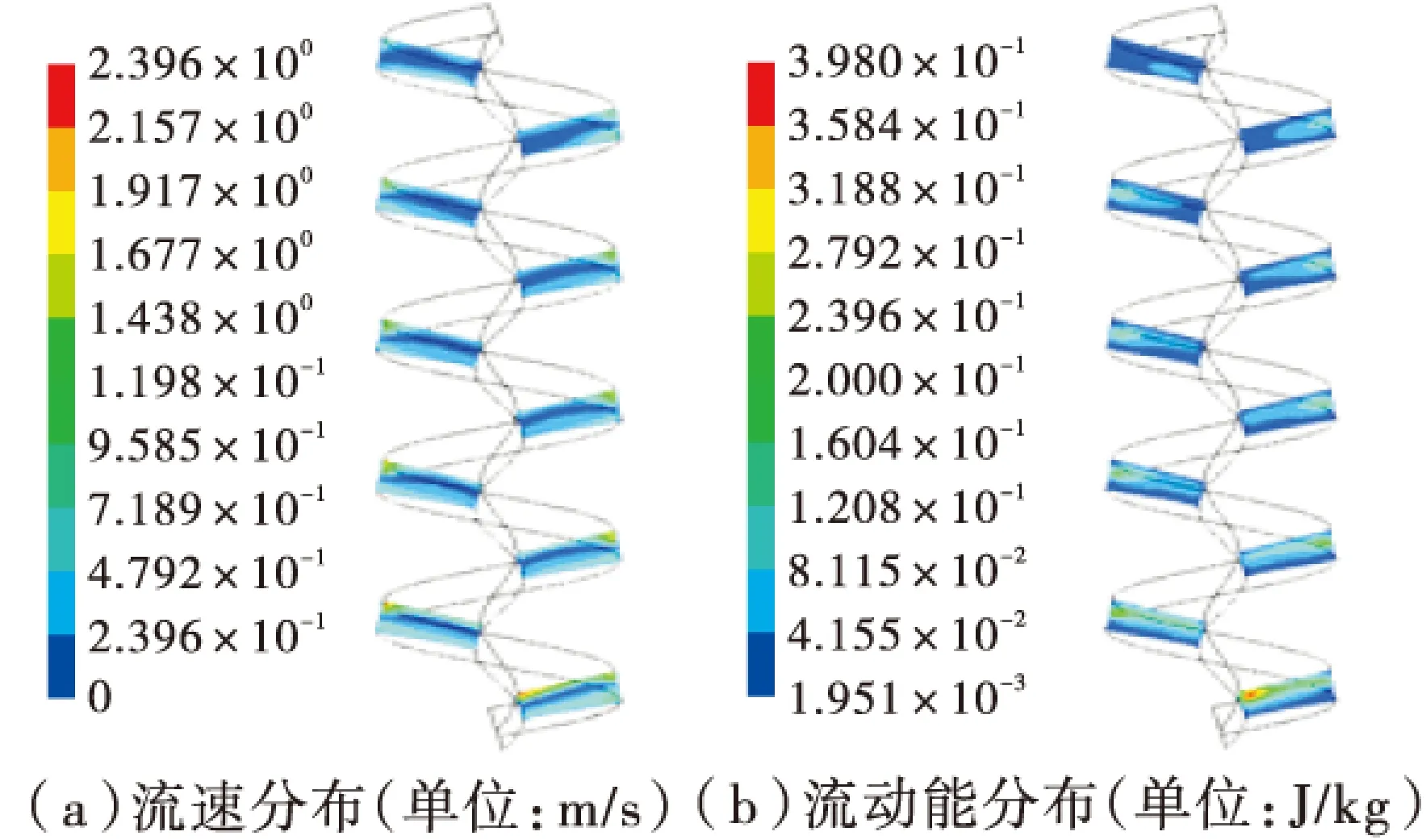
图5 螺距为240 mm时的流场特征
从图4、图5并结合图1、图2可以看出,当螺距从120 mm增大到180 mm和240 mm后,气相和液相交界面的位置没有明显的变化,因此该因素对水层厚度影响不显著;另一方面,螺旋溜槽的纵向倾角变大,流速和湍动能相应增加,近槽底处流速增幅约为0.07 m/s和0.10 m/s,这将使颗粒所受离心力增大,利于提高分选精度。
2.1.2.2 给矿流量的影响
仅将2.1.1节的给矿流量调整为10 L/min和15 L/min,轴向面上的流场分布特征分别见图6、图7。
从图6、图7并结合图1、图2可以看出,给矿流量增加后,流速和湍动能的基本分布特征不变,气水两相界面均有一定程度的上移,表明水层厚度有所增加。当给矿流量增至10 L/min时,流速和湍动能达到最大,继续增大给矿流量至15 L/min时,流速和湍动能有所降低。
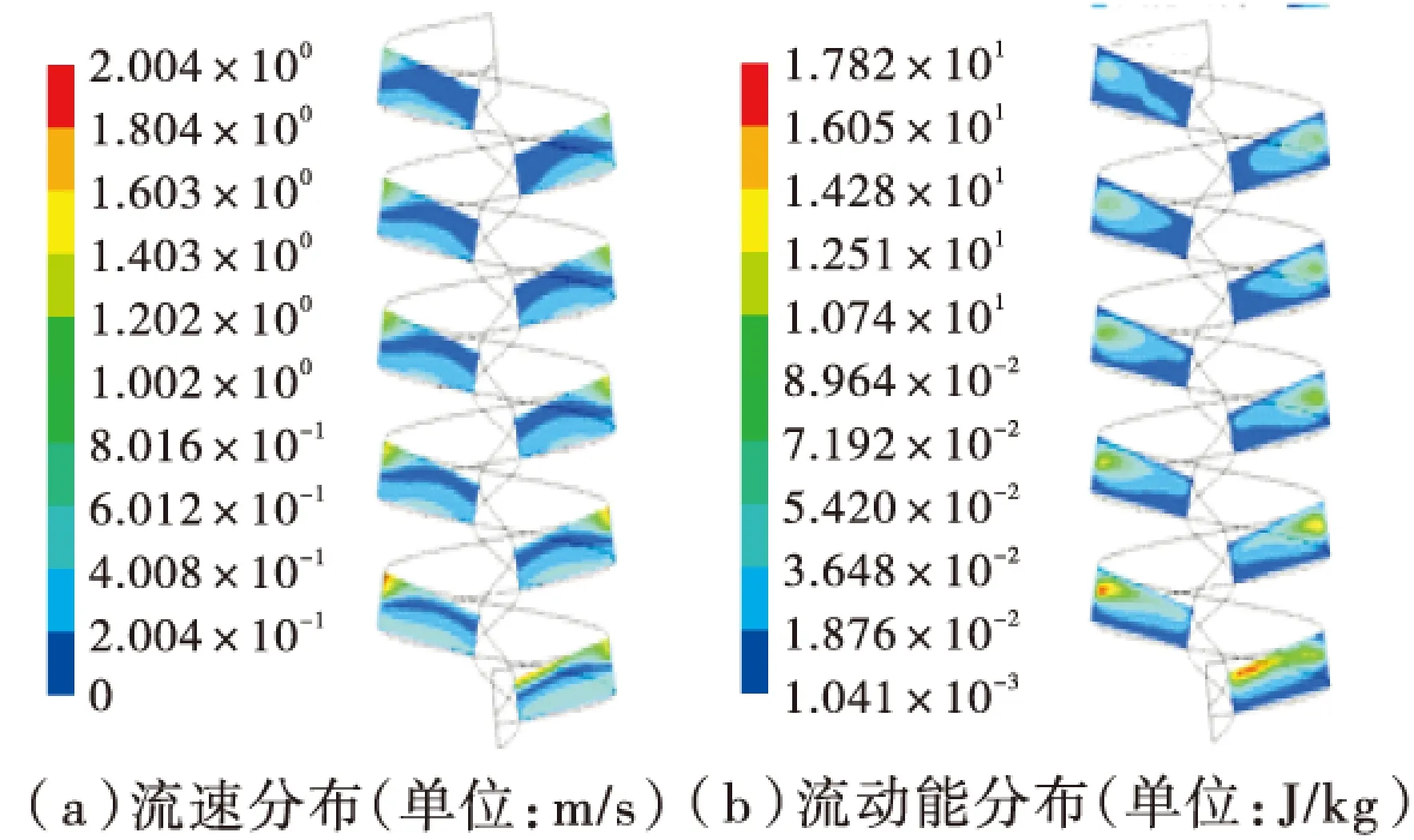
图6 给矿流量为10 L/min时的流场特征
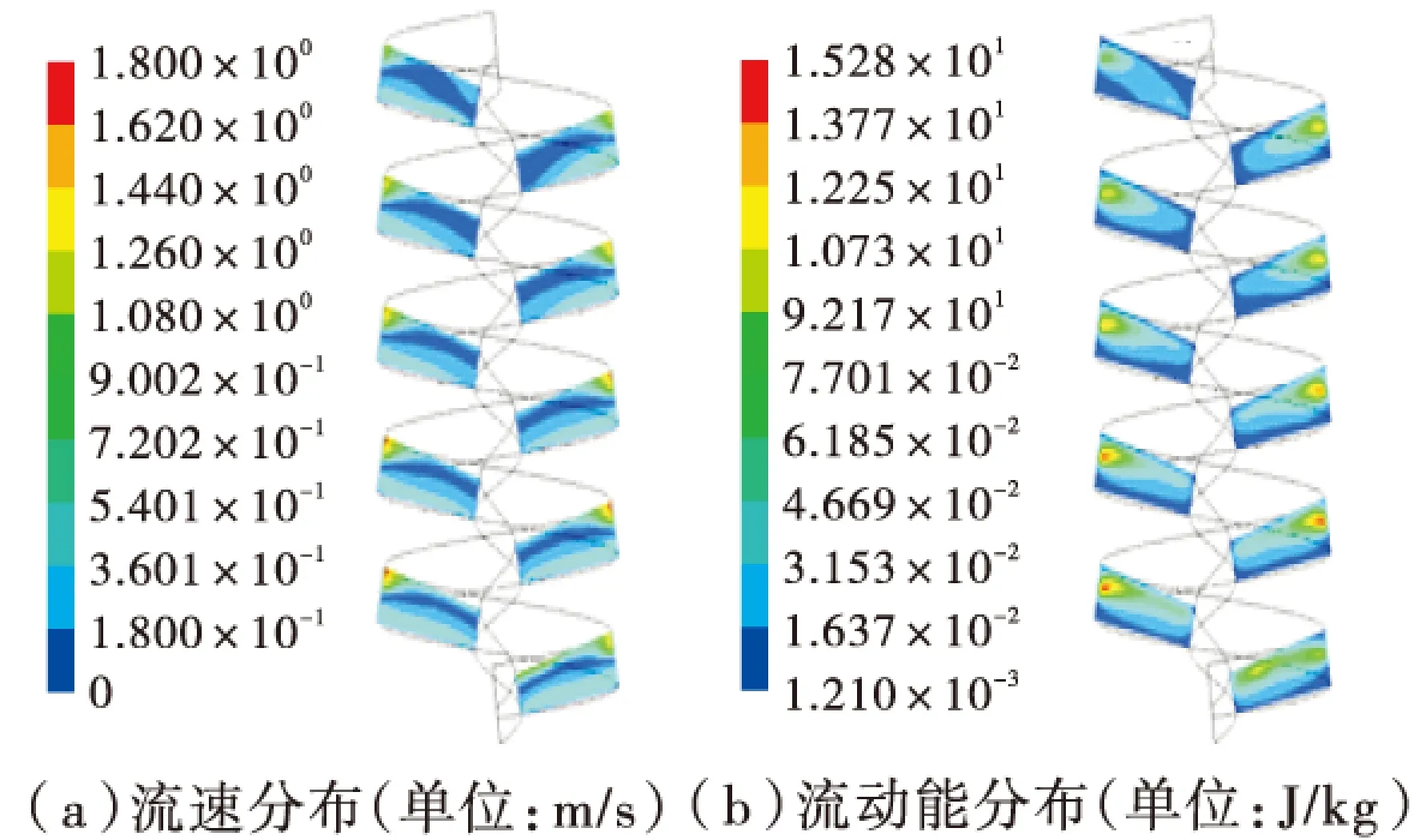
图7 给矿流量为15 L/min时的流场特征
2.2 颗粒在螺旋溜槽流场中的运动行为
在螺旋溜槽流场模拟的基础上,经相间耦合运算模拟,对颗粒的运动行为进行研究,进而探讨颗粒密度、螺距、给矿流量对颗粒运动行为的影响。
2.2.1 不同密度颗粒的运动行为差异
在螺距为120 mm、给矿流量为5 L/min的情况下,分别以粒度为20 μm的石英(2 675 kg/m3)、赤铁矿(5 000 kg/m3)和方铅矿(7 500 kg/m3)为对象,考察颗粒密度对物料在螺旋溜槽中运动行为的影响(数值模拟时假定颗粒从给矿口平面均匀给入),其运动轨迹见图8。
从图8可以看出,无论何种密度的颗粒,入口处均匀分布式给入后的向下运动过程即是逐渐集中的过程,大致在第4圈完成集中(即完成分带);在同样的轴向高度上,高密度颗粒的回转半径小于低密度的颗粒,因此,高密度颗粒从槽底排出的位置更靠近內缘,而低密度颗粒排出的位置则更靠近槽底的外缘。模拟结果与生产实践一致,表明数值模拟方法的可靠性。
2.2.2 螺距对不同密度颗粒的运动行为影响
仅将2.2.1节的螺距从120 mm调整为180 mm和240 mm,螺距对颗粒运动行为影响的规律模拟结果见图9、图10,螺距改变后颗粒速度值的变化规律见表1。
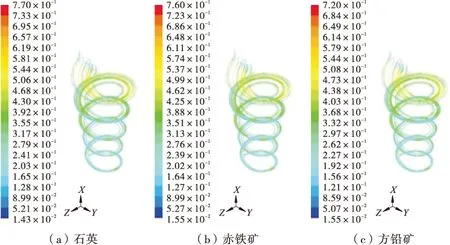
图8 不同密度的颗粒在螺旋溜槽中的运动迹线

图9 螺距为180 mm时颗粒的运动迹线
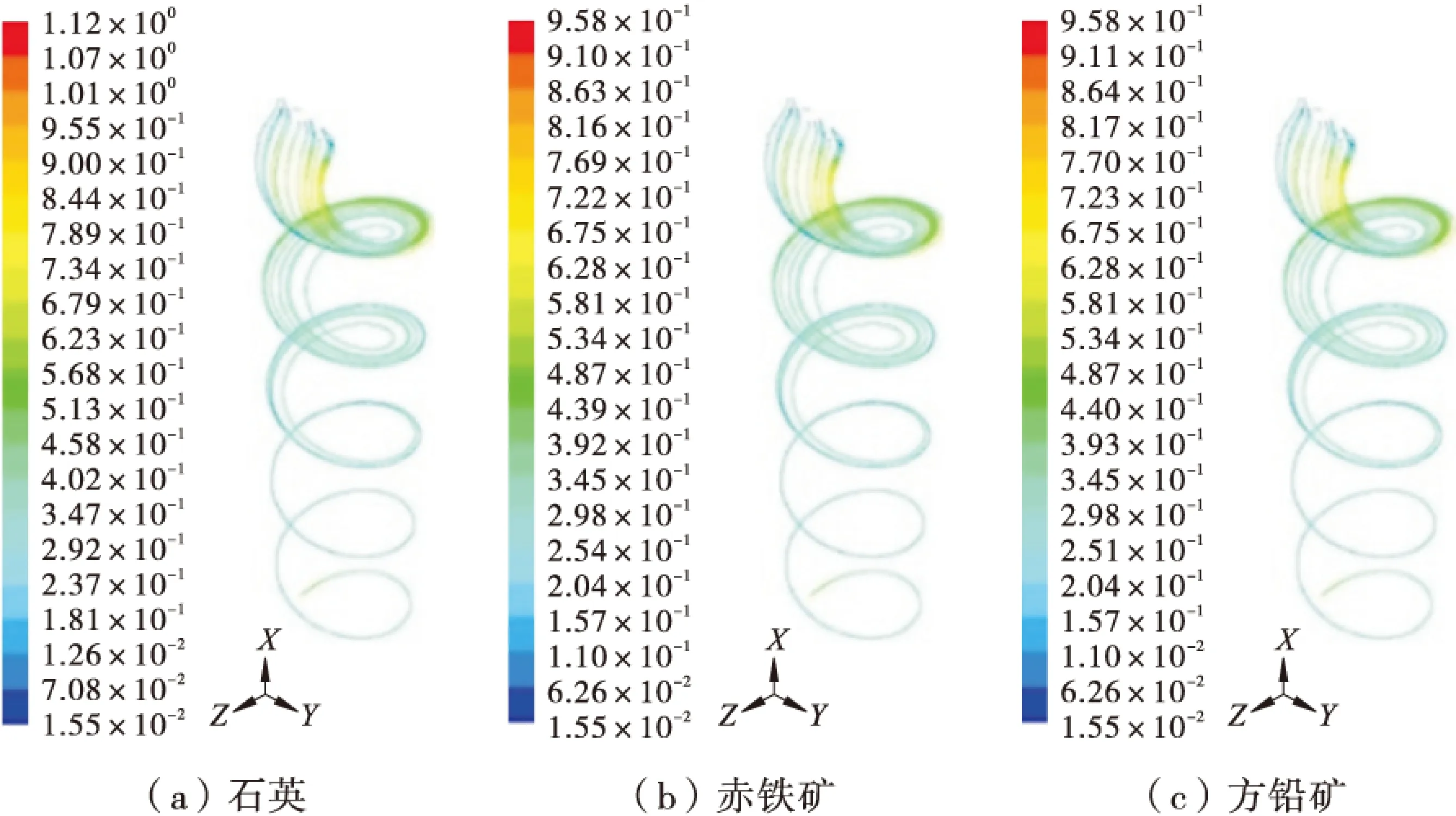
图10 螺距为240 mm时颗粒的运动迹线
从图9、图10并结合图8可以看出,螺距增大后,无论何种密度的颗粒,运动速度都明显提高,且沿螺旋线向下集中的趋势也更加明显,大致在第3圈即已基本完成集中(即完成分带)。
从表1可以看出,螺距增大,高密度颗粒的速度增幅更大,对高密度颗粒的运动行为影响更显著。因此,螺距增大,颗粒向外缘运动的趋势被加强。
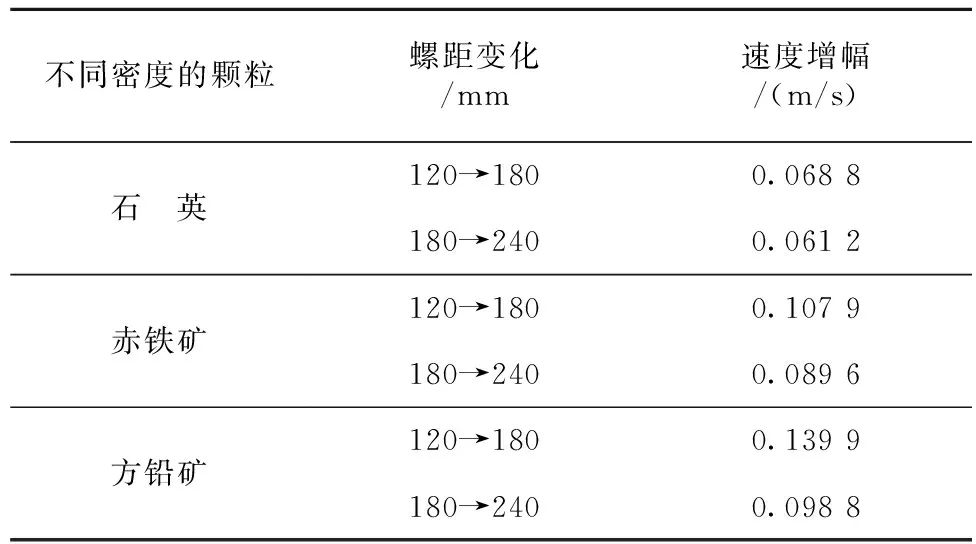
表1 螺距增大后颗粒的速度变化情况
2.2.3 给矿流量对不同密度颗粒的运动行为影响
仅将2.2.1节的给矿流量从5 L/min增至10 L/min和15 L/min,给矿流量对颗粒运动行为影响的规律模拟结果见图11、图12。
从图11、图12并结合图8可以看出,给矿流量增大后,颗粒的运动轨迹趋于分散,运动的随机性增大,对低密度颗粒的影响尤为明显,原来在第4圈可以完成的集中(即分带)延迟至第5圈末才基本完成。因此,增大给矿流量不利于分选,这是因为,流量增大导致流速和湍动能增大,颗粒的紊流受到较大影响,进而影响到颗粒的分选精度。
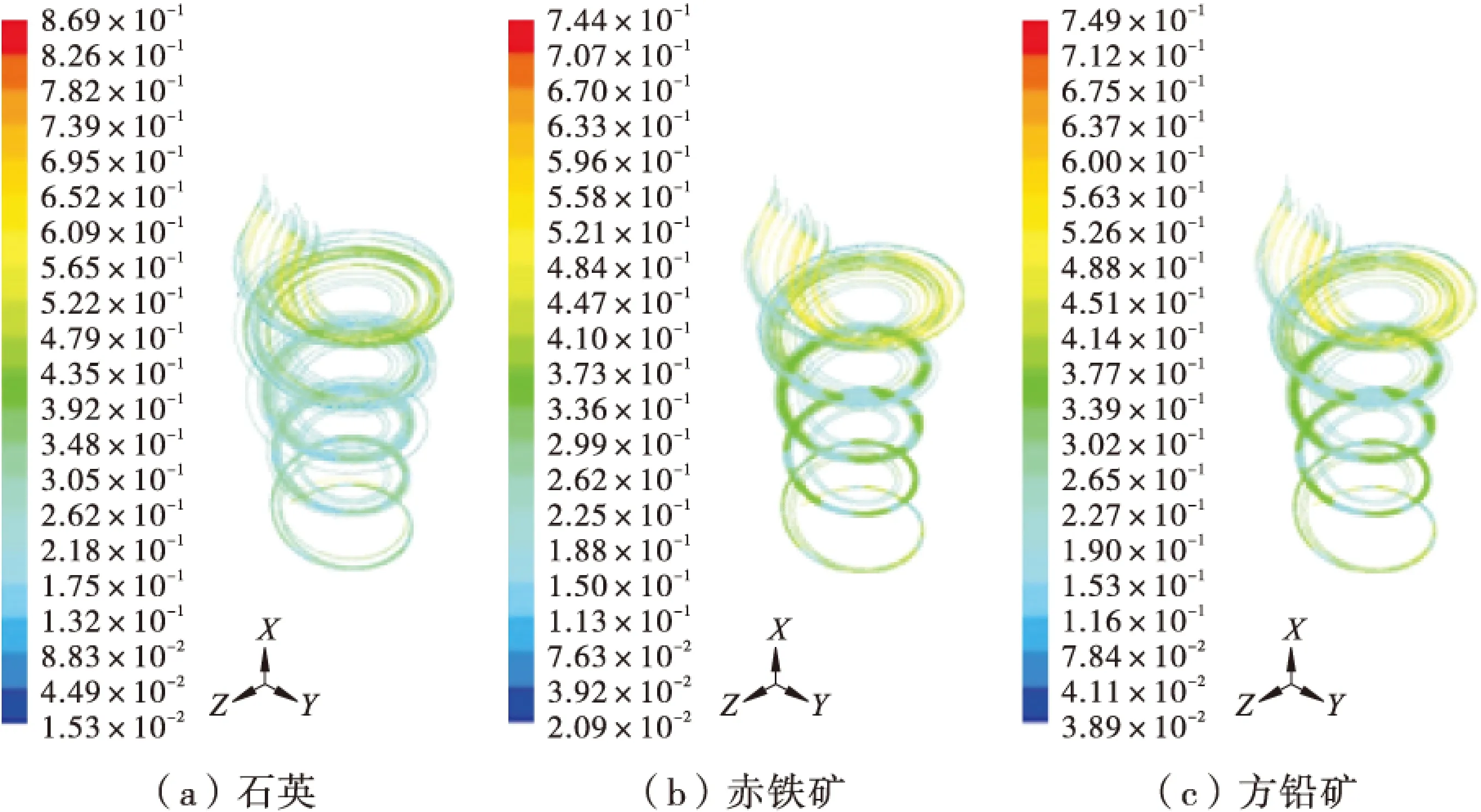
图11 给矿流量为10 L/min时颗粒的运动迹线
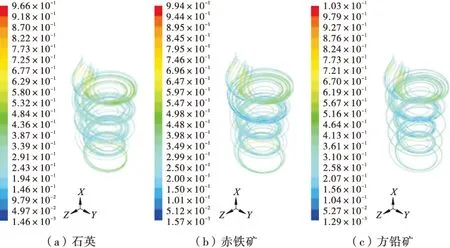
图12 给矿流量为15 L/min时颗粒的运动迹线
3 结 论
(1)流速等值线在轴向和径向上均呈条带状分布,水相流速沿槽深方向逐渐升高,沿径向从内向外逐渐增大;湍动能在径向上以类似于椭圆环状分布,外缘的紊流度从上至下逐渐升高。
(2)在相同的流场条件下,在同样的轴向高度上,高密度颗粒的回转半径小于低密度颗粒,且密度越大,速度极值越小。
(3)增大螺距对水层厚度基本没有影响,而水相流速和湍动能随之增加;增大螺距可使颗粒的运动速度明显增加,其对高密度颗粒的影响更大,有利于加速颗粒分带。
(4)增大给矿流量,气、水两相界面有所上移,表明水层厚度增加,而水相流速和湍动能在数值上均有不同程度的增大;给矿流量增大后,颗粒运动的随机性增大,尤其对低密度颗粒的影响更为明显,分带延迟,不利于分选过程的进行。
[1] 彭会清,李 广,胡海洋,等.螺旋溜槽的研究现状及展望[J].江西有色金属,2009,23(3):26-29. Peng Huiqing,Li Guang,Hu Haiyang,et al.Research actuality and prospect of spiral chute[J].Jiangxi Nonferrous Metals,2009,23(3):26-29.
[2] 陆朝波,孙翊洲,王万忠.广西某锡选厂提高枱浮摇床回收率的试验研究[J].矿产保护与利用,2013(4):25-28. Lu Zhaobo,Sun Yizhou,Wang Wanzhong.Experimental research on the improvement of tin recovery in table floating in a tin dressing plant in Guangxi[J].Conservation and Utilization of Mineral Resources,2013(4):25-28.
[3] 莫 峰,刘庆祥,张 军,等.螺旋溜槽在云南某锌锡矿的应用研究[J].有色金属:选矿部分,2013(1):77-80. Mo Feng,Liu Qingxiang,Zhang Jun,et al.Research on the application of spiral chute at the zinc-tin concentrator of Yunnan[J].Nonferrous Metals:Mineral Processing Section,2013(1):77-80.
[4] 陈中航,于克旭.某贫赤铁矿选厂合理工艺流程的试验研究[J].中国矿业,2013(2):81-85. Chen Zhonghang,Yu Kexu.Experimental research on the reasonable flowsheet on some lean hematite processing plant[J].China Mining Magazine,2013(2):81-85.
[5] 陈晓鸣,严 鹏,陈力行.磁性螺旋溜槽回收细粒钛铁矿试验[J].金属矿山,2014(3):132-135. Chen Xiaoming,Yan Peng,Chen Lixing.Application research of magnetic spiral chute on recovery of fine ilmenite[J].Metal Mine,2014(3):132-135.
[6] 金仁国,陆庆秋,于克旭,等.φ1 200 mm×720 mm锲形刻槽螺旋溜槽研制及试验研究[J].金属矿山,2000(1):46-48. Jin Renguo,Lu Qingqiu,Yu Kexu,et al.Development ofφ1 200 mm×720 mm wedged groove spiral sluice and its test research[J].Metal Mine,2000(1):46-48.
[7] 伍喜庆,黄志华.磁力螺旋溜槽及其对细粒磁性物料的回收[J].中南大学学报:自然科学版,2007,38(6):1083-1086. Wu Xiqing,Huang Zhihua.Magnetic spiral chute and its application in recovery of fine magnetic materials[J].Journal of Central South University:Science and Technology,2007,38(6):1083-1086.
[8] Murphy S,Delfosb R,et al.Prediction of strongly swirling flow within an axial hydrocyclone using two commercial CFD codes[J].Chemical Engineering Science,2007,62:1619-1635.
[9] Sutalo I D,Paterson D A,Rudman M.Flow visualization and computational prediction in thickener rake models[J].Minerals Engineering,2003,16:93-102.
[10] 刘 峰,钱爱军,郭秀军,等.DSM重介质旋流器流场的数值模拟[J].煤炭学报,2006,31(5):627-630. Liu Feng,Qian Aijun,Guo Xiujun,et al.Numerical simulation of flow field in the DSM heavy medium cyclone[J].Journal of China Coal Society,2006,31(5):627-630.
[11] Dong K J,Kuang S B,Vince A,et al.Numerical simulation of the in-line pressure jig unit in coal preparation[J].Minerals Engineering,2010,23:301-312.
[12] Xia Jiliang,Rinne Autti,Gronstrand Sami.Effect of turbulence models on prediction of fluid flow in an Outotec flotation cell [J].Minerals Engineering,2009,22:880-886.
[13] 魏德洲.固体物料分选学[M].北京:冶金工业出版社,2009. Wei Dezhou.Solid Materials Processing[M].Beijing:Metallurgy Industry Press,2009.
(责任编辑 罗主平)
CFD-based Numerical Simulation of Flow Field of and Particles Motion Behavior in Spiral
Gao Shuling Wei Dezhou Cui Baoyu Shen Yanbai Huang Xiuting
(College of Resources and Civil Engineering,Northeastern University,Shenyang 110819,China)
In order to ascertain the flow characteristics of spiral and separation behaviors of different mineral particles,numerical simulation of flow field of and particles motion behavior in spirals with diameter of 300 mm,was carried out by utilizingk-εmodel for turbulence calculation and VOF model for capturing the air-liquid interface and discrete phase model for the liquid-solid coupling based on the principle of CFD.The influence of spiral interval and feed mass flow on them was discussed as well.The results showed the water velocity isolines exist like obvious bands,its velocity magnitude increases gradually along the direction of spiral depth,and increases gradually from inner to outer along the radial direction.The turbulence kinetic energy appears like ellipse rings in the radial direction,and increases from top to bottom at the outer edge.In the same flow field,the maximum of particle motion speed has negative correlation to its density.When the spiral internal was enlarged,the water depth keeps invariant,however the water velocity and turbulence kinetic energy increased accordingly,and the particle motion speed increased as well,which could accelerate particles banding and separation.The feed mass flow has significant effect on the water depth,flow velocity and turbulence kinetic energy,however it has little influence on the flow distribution characteristics.The particle motion randomness is positively correlated to the factor,resulting in the delay of particles banding with the increasing of feed mass flow,which is disadvantage to the separation process.
Flow field of spiral,Particle motion,CFD,Numerical simulation,Spiral interval,Feed mass flow
2014-06-28
国家自然科学基金项目(编号:51104035),东北大学基本科研业务费项目(编号:N100301002)。
高淑玲(1980—),女,副教授,博士。
TD922+.3,TP15
A
1001-1250(2014)-11-121-06

