On measured-error pretreatment of bionic polarization navigation

GUAN Gui-xia(关桂霞), HAN Yu-zhang(韩愈章), WU Min-hua(吴敏华) LI Lei-lei(李磊磊)

(1.Information Engineering College, Capital Normal University, Beijing 100048, China； 2.Institute of Scientific Computing, University of Vienna，Vienna，Austria； 3.School of Automation, Beijing Institute of Technology, Beijing 100081, China)

On measured-error pretreatment of bionic polarization navigation

GUAN Gui-xia(关桂霞), HAN Yu-zhang(韩愈章)2, WU Min-hua(吴敏华)1, LI Lei-lei(李磊磊)3

(1.Information Engineering College, Capital Normal University, Beijing 100048, China； 2.Institute of Scientific Computing, University of Vienna，Vienna，Austria； 3.School of Automation, Beijing Institute of Technology, Beijing 100081, China)

A signal pre-treatment algorithm based on combination of 3-dimension system identification and Kalman filtering estimation (3DSKE) is proposed. The aim of designing the 3DSKE algorithm is to reduce errors caused by random noise, but leave the systematical errors caused by signal source remained to be solved by a special method. The 3DSKE algorithm is especially suitable for time series of pure measured data without dynamic equation and on-line real-time execution. The simulated result shows that the 3DSKE algorithm can help the basic theoretic calculation to realize feasible, stable, fast, high accurate and auto-executing computing process for the navigation applications.

polarization navigation; signal pretreatment; Kalman filtering; system identification

Bionic polarization navigation has been developed quickly and systematically, especially on its orientation mechanism and equipment[1-6]. However, the noise problems which must be considered during realizing the measure-calculation haven’t been adequatly discussed. There exist impact factors of polarization distribution and the output error, assembling error and random error of polarized-light sensor. Considering calculation result errors caused by signal source and measurement system, this paper adopts a signal pre-treatment algorithm to weaken the random errors. The 3DSKE algorithm is especially suitable for time series of pure measured data without dynamic equation and on-line real-time execution.

1 Parameter measurement

With the bionic polarization navigation technology, an object moving on the Earth-ground can recognize its own azimuth angleφ(relative to solar azimuth angle) through measurement-calculation. In the terrestrial coordinate system，the azimuth angle of the object can be calculated asα=φ+Aswhereαis the absolute azimuth angle of the object;Asis the solar azimuth angle (Fig.1).

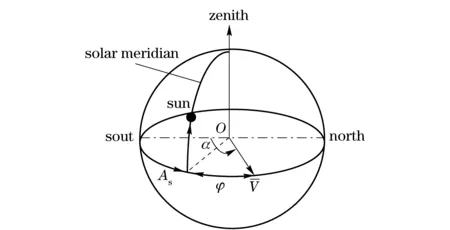
Fig.1 Relative azimuth angle described by terrestrial coordinate system

The measure-calculation process is executed as following:

① Measure 3 maximal output voltage values of the polarized-light sensing instrument,P1(φ,d),P2(φ,d)andP3(φ,d) (dis polarization degree of skylight).

The equations constructed byP1(φ,d),P2(φ,d) andP3(φ,d) are

(1)

(2)

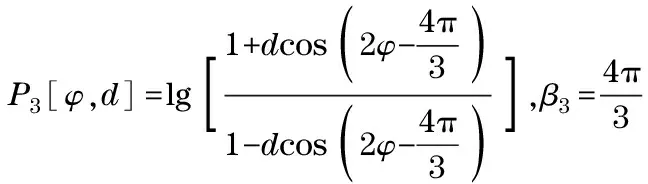
(3)

in whichβi,i=1,2,3 are angles between the major direction of polarized-light sensing instrument and long axes of the object.

② Using Eqs.(1)-(3) to construct 3 equation groups {(1),(2)}, {(2),{3}} and {(1),(3)}.

③ Solve the equation groups to get 3 solutions.

The criterion used for selecting the reasonable solution mentioned above is described as

(4)

Whenmeasured-errorexists,thecondition“minimizing|f|” can be taken to approximate Eq.(4). Using Eq.(4) as the criterion, select a most reasonable solution from the three solutions mentioned above. The value ofφinvolved in the reasonable solution is the expected relative azimuth angle of the object.

The basic calculations ofφanddmentioned above, denoted as the core algorithm in this paper, were already described in other papers[7-11]. In fact, a measured value of any one ofP1(φ,d),P2(φ,d) andP3(φ,d) will be a sum of true value and error value, this leads to non-accurate solutions of equation groups mentioned above and difficult approach of criterion (4). Based on the consideration described above, we developed and tested a measured-value pretreatment algorithm (3DSKE algorithm) based on combination of 3 dimension system identification[12-14]and Kalman filtering estimation[15-16]described as bellow. This algorithm can help the basic theoretic calculation to realize stable and high accurate auto-executing on the navigation application.

2 Measured value pretreatment using 3DSKE

2.1 State space model and estimation of measured values

Supposing that 3-dimentional observation value time series ofP1(φ,d),P2(φ,d) andP3(φ,d), symbolized as {p1(k),p2(k),p3(k)},k=1, 2, …, were obtained from 3 outputs of the polarized-light sensing instrument at timek, which can be approximated using a second power Taylor Expansion. According to Kalman filtering theory, this observation values can be described by a 3-demensional state space model (without dynamical terms) as Eqs.(5) (6). Under proper condition (integral continuous), their states can be optimally estimated. The state space model equation and observation equation are

x*(k)=A(k)x*(k-1)+G(k)ξ(k-1),

(5)

z(k)=C(k)x*(k)+η(k),

(6)

in which， {ξ(k)} and {ηk)} are independent Gauss-white-noise vectors；z(k) is observation vector of the polarized-light sensing instrument.

Some related concepts are defined bellow.

① Define model input as

φT(k-1)=[p1(k-1),p1(k-2),p1(k-3),

p2(k-1),p2(k-2),p2(k-3),

p3(k-1),p3(k-2),p3(k-3),

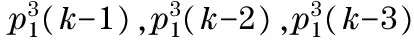
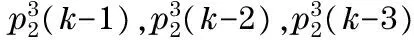
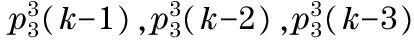
p1(k-1)×p2(k-1),p1(k-2)×p2(k-2),

p1(k-3)×p2(k-3),

p2(k-1)×p3(k-1),

p2(k-2)×p3(k-2),

p2(k-3)×p3(k-3),

p1(k-1)×p3(k-1),

p1(k-2)×p3(k-2),

p1(k-3)×p3(k-3)],

(7)

in which the 3 power terms and product terms function for approximating the non-linear characteristic of the model, and the time-shift-treatments for dynamic property of system;

② Define the model parameter vector as

(8)

inwhichai1…ai27are real numbers used as model parameters.

③ Define a state vector of true-values as

x*(k)=[φ(k)]27×1.

(9)

④ Define a transition-matrix as

A(k)=

(10)

⑤ Define the observation matrix as

(11)

Thus, when all elements in the transition-matrixAare optimally estimated, 3DSKE algorithm based on models Eqs. (5) (6), can be executed.

2.2 Model parameter estimation

A model form structured in 1-step-forecast difference-equation expressed as Eq.(12) was used for non-linear system identification execution, following from the principle of system identification theory[10-11], and it is set up for realizing the model parameter estimation:

yj(k)=φ*T(k)×θj(k),j=1,2,3,

(12)

which describes 6 models with different approach-forecast goals individually:

(13)

(14)

With simulated output:

(15)

InEq.(14), {evj(k)},v=1,2;j=1,2,3 are independent Gaussian-white-noise with zero-average involving the effects from {ξ(k)} and {η(k)}. Under the condition that {ξ(k)} and {η(k)} are independent Gauss-white-noise vectors, the model parameter estimation can provide unbiased regression estimators ofθT(k), and under the condition that {ξ(k)} and {η(k)} are independent Gauss-white-noise vectors the Kalman filtering can provide unbiased regression estimators ofx*(k).

2.3 3DSKE algorithm

The practical full on-line algorithm for determining the relative azimuth angle of an object moving on the Earth-ground is summarized in the following block-flow-graphics.

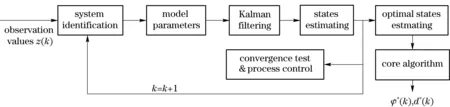
Fig.2 3DSKE algorithm

3 Simulation experiment

Using 150 groups of simulated values ofP1(φ,d),P2(φ,d) andP3(φ,d), denoted asp1(φ,d,k),p2(φ,d,k), andp3(φ,d,k),k=1,2,…,150. The experiment is implemented in the following steps:

① Simulate practical measured values of noise-signal-ratio=25% denoted asp″1(φ,d,k),p″2(φ,d,k), andp″3(φ,d,k) (Fig.3), by adding computer simulated error values toP1(φ,d),P2(φ,d) andP3(φ,d).

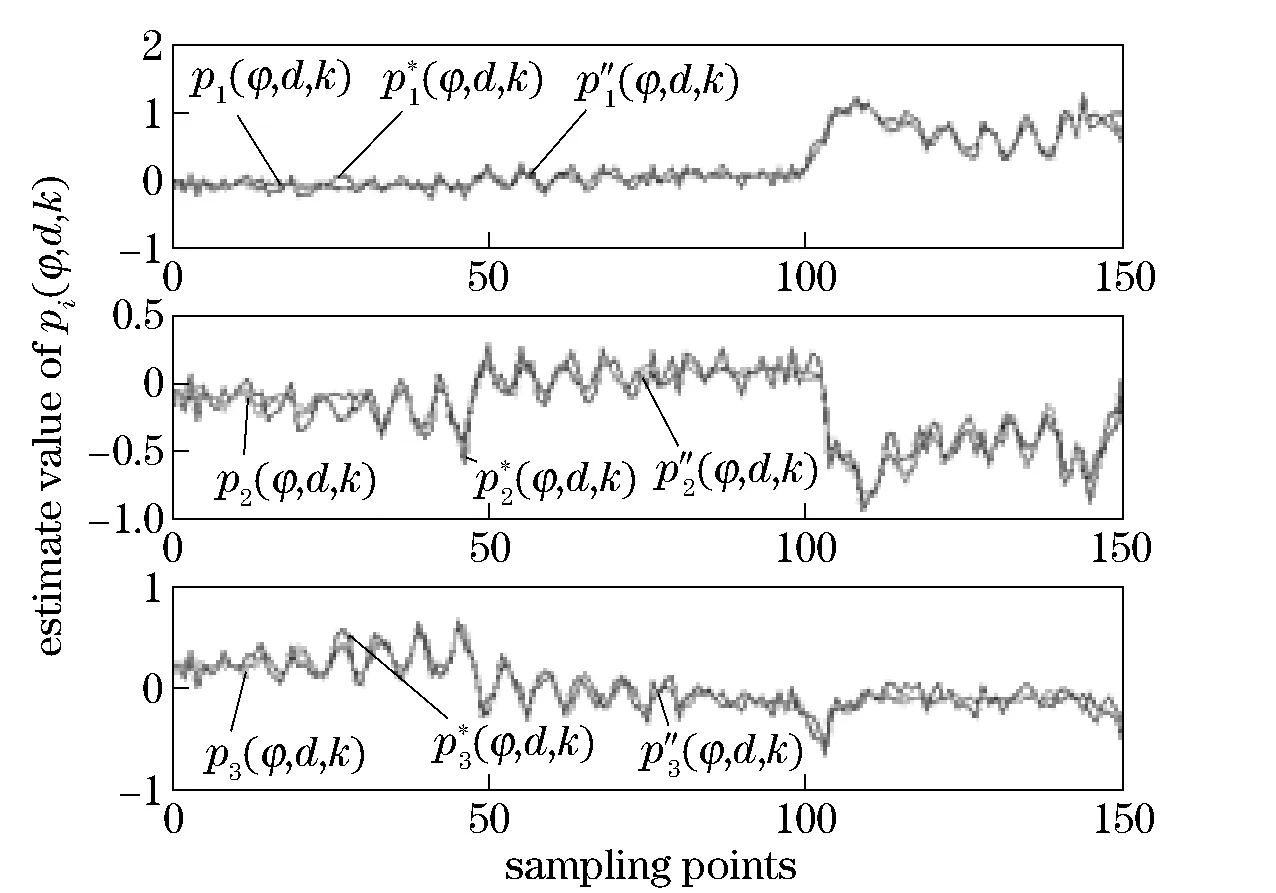
Fig.3 Pretreatment of P1(φ,d),P2(φ,d) and P3(φ,d)

② Simulate true values ofφandddenoted asφ(k) andd(k),k=1,2,…,150 , using Eqs.(1)-(4) (Fig.4).

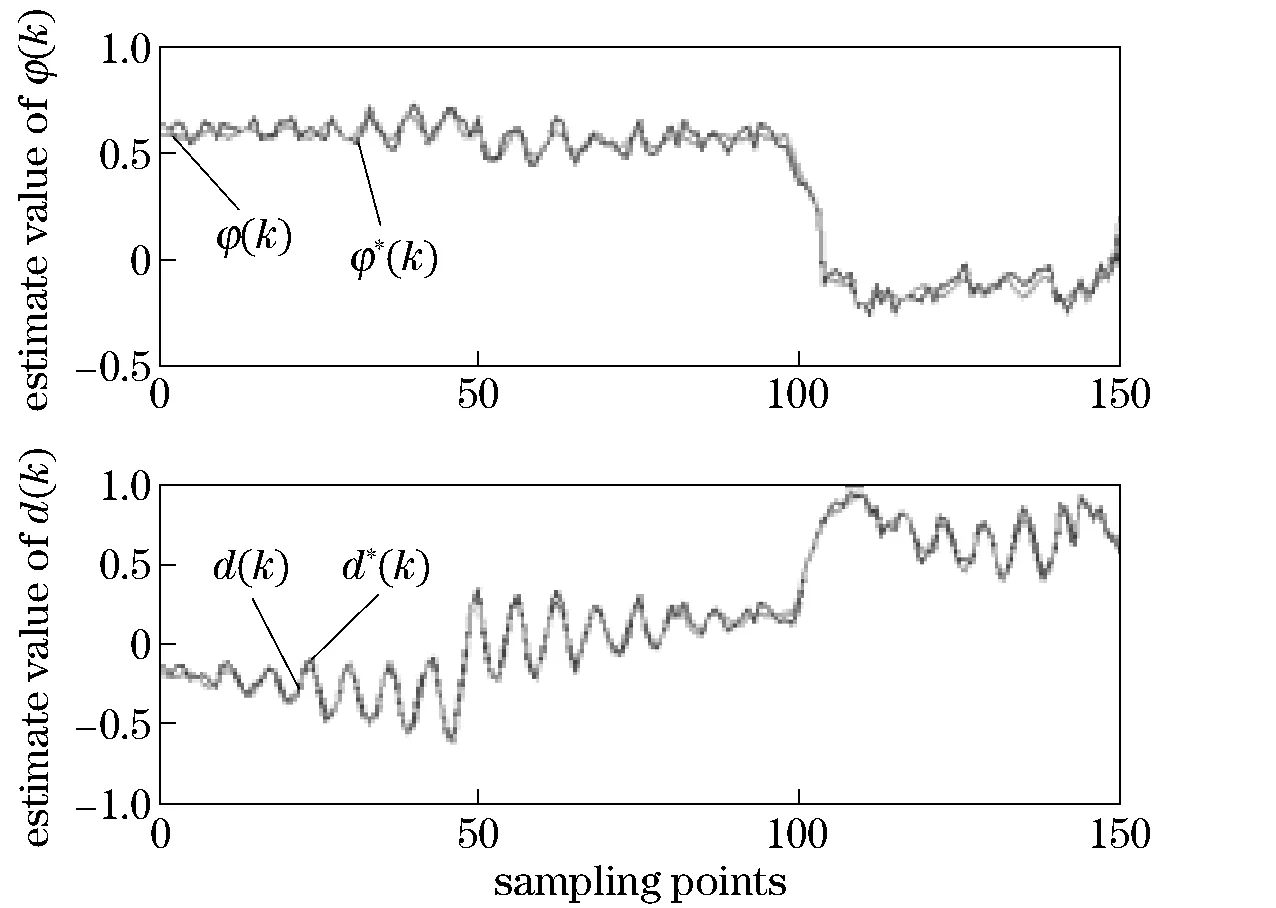
Fig.4 Optimal estimate of φ(k) and d(k)

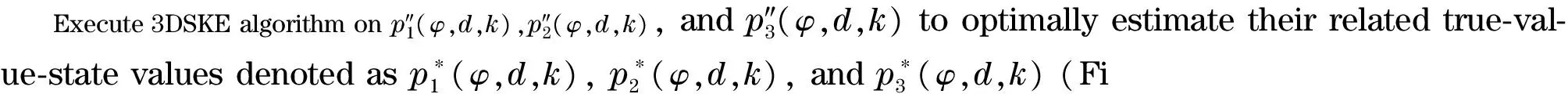
④ Execute the CA-algorithm to produce the respected optimal estimation values ofφwithddenoted asφ*(k) andd*(k),k=1,2,…,150 (Fig.4).

Based on the simulation results above, the statistical accuracy index value of estimatedφ*(k) comparing with their simulated true valuesφ(k) was calculated as

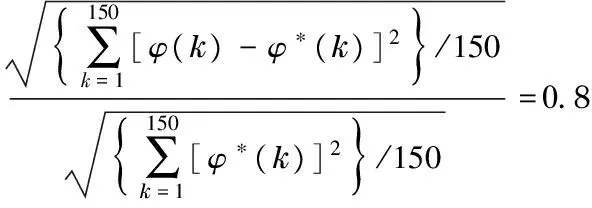
(16)

4 Conclusion

A special data pretreatment algorithm based on combination of system identification and Kalman filtering is proposed, which is used to determine high-accuracy relative azimuth angle for object moving on the earth-ground. The core algorithm was implemented and tested with 150 measured data groups. The experiment results show that the statistical accuracy (signal to noise ratio) of 150 optimally estimated values of relative azimuth angles range within 1% under the condition of strong measured-noise (signal to noise ratio=25%). This result shows the algorithm is smooth and stable, which can provide a feasible location-determination method for the fields such as spaceflight, navigation, and robot moving control, and so on.

[1] Michael L Brines. Dynamic patterns of skylight polarization as clock compass[J]. J Theor Biol, 1980,86:507-512.

[2] Samuel Rossel, Rudiger Wehner. The bee’s map of the e-vector pattern in the sky[J]. Proc Natl Acad Sci, 1982,79:4451-4455.

[3] Karl Fent, Rudiger Wehner. Oceili: A celestial compass in the desert ant cataglyphis[J]. Science, 1985, 228: 192-194.

[4] Able K P, Able M A. Calibration of the magnetic compass of a migratorty bird by celestial rotation[J]. Nature, 1990,347:378-380.

[5] Reppert S M, Gegear R J, Merlin C. Navigational mechanisms of migrating monarch butterflies[J]. Trend in Neurosciences, 2010,33(9):399-406.

[6] Cronin T W, Marshall J. Patterns and properties of polarized light in air and water[J]. Philosophical Transactions of the Royal Society B:Biological Sciences,2011,366(1565):619-626.

[7] Dimitrios Lambrinos, Ralf Moller, Thomas Labhart, et al. A mobile robot employing insect strategis for navigation[J]. Robotics and Autonomous Systems, 2000,30:39-64.

[8] Schmolke A, Mallot H, Neurowissenschaft K. Polarization compass for robot navigation[C]//The Fifth German Workshop on Artificial Life,2002:163-167.

[9] Dimitrios Lambrinos. Navigation in desert ants:the robotic solution[J]. Robotica, 2003, 21:407-426.

[10] Thakoor S, Chahl J, Srinivasan M V, et al. Bioinspired engineering of exploration systems for NASA and DoD[J]. Artificial Life, 2008,148:75-82.

[11] Chu Jinkui, Chen Wenjing, Wang, Hongqing, at el. Mobile robot navigation tests with polarization sensors[J]. Optics and Precision Engineering, 2011,19:2419-2426.

[12] Fattah Shaik A, Zhu Weiping, Ahmad M O. A novel technique for the identification of ARMA systems under very low levels of SNR[J].IEEE Transactions on Circuits and Systems I: Regular Papers, 2008, 55(7): 1988-2001.

[13] Soize C. A computational inverse method for identification of non-Gaussian random fields using the Bayesian approach in very high dimension[J]. Computer Methods in Applied Mechanics and Engineering, 2011, 200(45-46):3083-3099.

[14] Chlewicki Wojciech, Baniukiewicz Piotr, Chady Tomasz, et al. Identification of the position of objects in three dimensions using an extended radiography system[J]. International Journal of Applied Electromagnetics and Mechanics, 2012,39(1-4):167-173.

[15] Yazdanian M, Mojiri M, Sheikholeslam F. An extended Kalman filter for identification of biased sinusoidal signals[C]∥ICEE 2012-20th Iranian Conference on Electrical Engineering, 2012:990-993.

[16] He Zhengbin, Nie Jianliang, Wu Fumei, et al. Kalman filtering algorithm based on random design matrices with application to integrated GNSS/INS navigation[J]. Journal of Wuhan University,2012,37(9):1036-1040.(in Chinese)

(Edited by Wang Yuxia)

2013- 02- 28

Supported by the National Natural Science Foundation of China(61174220); the Project of Beijing Municipal Education Commission(KM201210028002); Weapon Equipment Development Project(9140A09050313BQ01127)

V 249.32 Document code: A Article ID: 1004- 0579(2014)02- 0235- 05

E-mail: guanguixia@sina.com