生态工业园共生网络的脆弱性

李湘梅, 肖人彬, 曾 宇, 姚智爽

(1. 湖北经济学院, 武汉 430205; 2. 华中科技大学系统工程研究所, 武汉 430074;3. 华中科技大学文华学院, 武汉 430074)

生态工业园共生网络的脆弱性

李湘梅1,*, 肖人彬2, 曾 宇2, 姚智爽3

(1. 湖北经济学院, 武汉 430205; 2. 华中科技大学系统工程研究所, 武汉 430074;3. 华中科技大学文华学院, 武汉 430074)

工业生态系统的稳定可持续运行是生态工业园区实现环境效益、经济效益和社会效益的重要保障，对生态工业共生网络脆弱性分析是工业生态学领域值得探讨的重要问题。运用复杂网络理论，从网络拓扑结构出发，论证该工业园具有小世界性和无标度性，为网络脆弱性分析奠定基础；通过攻击负载最大节点，利用网络效率和最大连通子图对网络的脆弱性进行分析，从而衡量节点失效对整个网络造成的破坏性。指出复杂网络在生态工业园共生网络中进一步研究的方向。

工业园；共生网络；脆弱性；拓扑性质

工业共生是指某个产业集群中的不同企业之间通过资源交换来实现经济效益和环境效益，它属于工业生态学领域的重要研究内容之一[1]。工业共生网络则是许多企业和企业间通过物质交换、能源传递以及知识、人力和技术资源的交换形成的长期共生关系构成的集合，从而实现环境效益和竞争效益的目标[2]。生态工业园作为工业共生理念的具体实践形式，自20 世纪70 年代以来，开始成为世界产业园区发展领域的主题，很多国家都在积极的探索其有效的模式，如丹麦、美国、荷兰、澳大利亚、日本、韩国、中国等。在我国，生态工业园被认为是继经济开发区和高新园区后的又一种新型工业园发展模式，目前正积极批准兴建的工业园区的数量迅速增加。然而，生态共生系统由于其独特的生态化产业链接属性和成长环境，运行过程中面临着各种各样的风险和不稳定因素，造成大量不稳定问题逐步出现并且已经成为影响工业生态系统取得成功的重要障碍[3- 4]。因此，对生态工业共生系统的脆弱性进行分析和评价，提出相应的保护策略，对于工业园区的稳定、安全运行具有重要的理论意义和现实意义。

工业共生网络是包含工业共生关系的新型生产组织模式，是企业生态合作的主要组织形式，它具有产业生态系统和网络组织的双重属性。国内外学者关于工业共生网络问题做了大量探索和研究，Mirata等研究了生态工业网络中企业共生对区域环境的进化作用[2]，Tan等以整数规划模型与启发式算法解决网络规划问题[5]，袁增伟等从环境伦理入手阐释了产业共生网络中企业需要承担的五类环境责任，并探讨了生态工业园产业共生网络的形成和运作机制[6]。王兆华将威廉姆森关于费用交易理论的3个决定因素——资产专用性、交易频率和不确定性运用于工业共生机理的研究，阐述了企业建立密切交易关系的动力和愿望[7]。近年来，研究者在工业共生网络稳定性方面取得一定进展，主要集中在稳定性内涵的界定和其影响因素的研究[4]，邓华提出了产业生态系统稳定性影响因素的三维理论模型[8]，这些研究都是基于提高工业园区稳定性而提出的各种策略研究，并未涉及对稳定性的数量化评价。罗柳红从拓扑学和图论理论的角度来探讨生态工业园区的稳定性问题，并提出园区系统维稳的调控手段[9]；李勇建立了加权产业共生局域网络模型，旨在揭示工业共生网络中噪声传播(文中将网络中不良信息、较差的信誉、信用等的传播统一规定为噪声机理传播)规律对网络的稳定性影响[10]。这些研究尽管都从网络结构出发对网络稳定性进行研究，但重点关注网络静态稳定性，或考虑的影响因子单一(如噪声)。可见，上述研究在处理网络稳定性问题上都存在缺陷。

结构决定功能是系统科学的基本观点，强调系统的结构并从结构角度分析系统的功能正是复杂网络理论研究的基本思路。近年来兴起的复杂网络理论为大型复杂网络统计特征的研究提供了新的思路。自1998年6月，美国康奈尔(Cornell)大学理论和应用力学系的博士生Watts及其导师Strogatz在Nature杂志上发表了题为《“小世界”网络的群体动力行为》的文章，建立了小世界模型[11]，以及1999年10月，美国圣母(Notre Dame)大学物理系的Barabasi教授和博士生Albert在Science杂志上发表了题为《随机网络中无标度的涌现》一文，建立了一个无标度网络(Scale-free networks)模型(BA网络模型)[12]以来，直接推动了研究者从简单的规则网络转向复杂网络的研究，进而掀起了复杂网络研究的空前浪潮，其研究已经渗透到生物学、医学、计算机科学、社会学、管理学和生态学等众多领域，目前已成为复杂性科学的研究热点。采用复杂网络理论对生态共生网络进行研究已取得一定进展[13- 15]，主要集中在共生网络拓扑性质分析，对工业共生网络的脆弱性分析还未涉及。这里要特别指出的是，系统的脆弱性是指系统在受到各种扰动的情况下，系统能够维持自身工作状态的能力。它与稳定性是分别从正反两方面来反映这种能力，即反映系统的同一本质内容[16]。本文采用脆弱性这一术语，还在于复杂网络领域中有关脆弱性的研究较多。鉴于此，本文运用复杂网络理论，从网络结构出发，在确定工业园区关键节点基础上，采用攻击负载最大节点策略，利用网络效率和最大连通子图对网络的脆弱性进行分析。这不仅有利于拓展工业园新的研究视角，而且可为工业园区稳定运行、提高网络故障后弹性修复能力打下基础，从而为我国工业园区的规划、建设和发展提供技术支撑。

1 工业共生网络的构建

1.1 工业共生网络复杂性特征

生态工业园是指依据清洁生产要求、循环经济理念和工业生态学原理而设计建立的一种新型工业园区，它通过物质流或能量流传递等方式把不同工厂或企业连接起来，形成共享资源和互换副产品的产业共生组合，使一家工厂的废弃物或副产品成为另一家工厂的原料或能源，模拟自然生态系统，在产业系统中建立“生产者-消费者-分解者”的循环途径，寻求物质闭环循环、能量多级利用和废物产生最小化[17]。如果将生态工业系统内部的各个企业作为节点，各企业之间的关系视为连接，那么该生态工业系统就构成了一个网络，称为工业共生网络[2,6]。网络复杂性，是指网络个体单元不具有，必须通过网络整体涌现、介于有序和无序之间的一类性质。一般而言，网络系统的复杂性主要体现在3个方面[18]：

(1)结构复杂性

网络连接结构看上去错综复杂、极其混乱,而且网络连接结构可能是随时间变化的。

(2)节点复杂性

网络中的节点可能是具有分岔和混沌等复杂非线性行为的动力系统，一个网络中也可能存在不同类型的节点。

(3)各种复杂性因素的相互影响

实际的复杂网络会受到各种各样因素的影响和作用,各种网络之间存在复杂的相互作用。根据网络复杂性的以上特点，可认为生态工业园具有典型复杂网络的特征。具体说明如下：

①工业共生网络是生态工业园内企业生态合作的主要组织形式，其结构具有复杂性。工业共生关系是指通过生态园区内不同企业之间相互利用副产品的合作，共同提高企业的生存及获利能力，达到节约资源和保护环境目的的产业关系。一般园区的生态产业链既包括串联耦合，又包括并联耦合，也可把单一的串联耦合和并联耦合形式的链条经过多重耦合，形成一个生态网络系统。

②生态工业园中企业类型的多样性使得网络结构的具有复杂性。生态工业园是由多种产业链组成的一种新型工业组织形态，必然存在多种类型的企业；为在工业系统中建立生态循环，园区内的企业需分别承担“生产者”、“消费者”、“分解者”等角色，这些企业属于不同行业或产业，拥有不同规模，同时在网络中的重要度也不同，呈现出多样性。

③生态工业共生网络会受到各种各样因素的影响使得共生关系复杂多变。随着生态工业园实践的开展，由于国家政策的变化、市场供需、新能源新材料出现、技术因素、经济支持等，各企业之间的连接关系可能在连接类型、共生关系的紧密程度、共生关系的有无以及企业之间连接方向和权重等发生变化，从而使得共生网络呈现复杂动态关系，严重会威胁到系统的稳定运行。

1.2 生态工业园共生网络的拓扑结构

本文以某化工工业园为案例，该生态工业园主要将传统煤化工产业(如煤制甲醇)与新型煤化工产业(如煤制烯烃、煤制油)结合，生成了SNG、聚丙烯腈、聚乙烯、PTT、PET、聚甲醛、γ-丁内酯、四氢呋喃、石脑油、柴油、煤沥青等多种市场需求量大、应用范围广的产品。其中聚乙烯是世界上用量最大的合成树脂，主要应用于中空制品、注塑制品、线材等；聚对苯二甲酸丙二醇酯(PTT)是种极具发展前途的新型聚酯高分子材料，1998年被美国评为六大石化新产品之一，在地毯工业、服装材料、工程热塑料等众多领域应用前景十分广阔；聚甲醛是世界五大工程塑料之一，有“夺钢”、“超钢” 之称，可广泛应用于替代钢铁、铜、锌和铝等金属材料做许多部件。该工业园按照产业关联度强、生产集约度高、资源节约、环境友好的原则，以打造煤炭、煤化工、煤炭深加工及综合利用为三大支柱产业的现代化、可持续发展的大型能源集团为目标，分阶段规划并推进生态工业建设。该工业园通过产品流、能量流和废弃物流交换建立产业共生关系，其主要链接为：① 煤矿→热电厂→建材厂；② 煤矿→煤炭深加工→聚乙烯、聚甲醛、PPT、PET等；③ 自来水→煤化工、盐化工、玻璃建材等→污水处理厂→中水回用。该工业园区各链条之间通过物质、能量、信息的流动和共享，彼此交错、横向耦合，使整个共生体形成了网状结构。图1为该生态工业园简图。

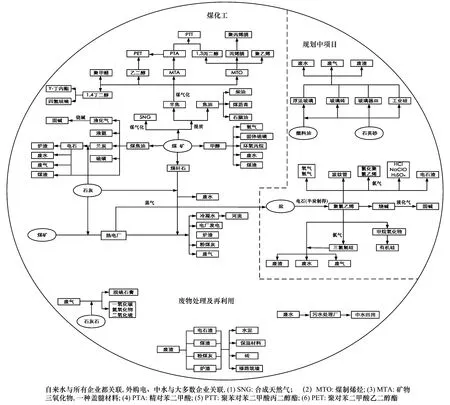
图1 煤化工工业园简图Fig.1 Brief System Network of coal chemical Industrial Park

本文以工业园区内部及周边地区企业为节点，企业之间的物质、能量和信息交换作为边。尽管工业园网络中企业之间存在物质、能量和信息流动的方向性问题，但互利共生是所有产业共生关系中最为常见的[7]。关于生态工业园稳定性分析中，有研究者指出当共生网络中一个企业的生产经营情况出现问题，可能会导致整个共生链条上的企业生产运营陷入瘫痪。下游企业用于生产的原材料主要来自于上游企业生产的废弃物或副产品，下游企业的生产将在很大程度上依附于上游企业，增加了下游企业生产运营的不稳定因素，同样，上游企业的生产运营情况也在很大程度上受到下游企业生产运营情况的影响，进而导致生态工业园产业共生网络的不稳定[3, 19]。可见，工业共生网络运行中企业间是相互影响的。本文抛开了纷繁复杂的物质、能量、信息等的交换关系，从企业间互利共生和相互作用影响的角度出发，同时考虑到复杂网络理论在生态工业园的研究处于起步阶段，将生态工业网络简化为一个无向、无权网络来研究。根据该案例中72个企业的相互关系得出邻接矩阵，并利用Ucinet6.0软件NetDraw工具，得到图2所示的该生态工业园网络拓扑结构。

图2 工业园区拓扑结构图Fig.2 The topology of eco-industrial parks

2 网络拓扑性质分析

生态工业园共生网络表现出复杂网络形态，对其网络拓扑性质进行分析，可为进一步研究生态工业园共生网络的各种性能(如脆弱性)奠定基础。网络拓扑参数是研究网络特性最基本工具，本文采用的主要参数有度、度分布、网络直径、平均最短路径长度、聚类系数等指标，这些参数的定义和计算公式详见文献[20- 22]。本文采用MATLAB7.0编程实现以上统计量的计算，计算结果见表1。由表1可知，该生态工业园企业个数N为72个，企业间的边M是142，网络的平均度为4.9378，平均最短路径长度L为3.6759，网络直径D为7.1450。在此基础上对该生态工业园共生网络的基本拓扑性质，即无标度性和小世界性进行分析。

表1 生态工业网络的统计特征参数

2.1 无标度性

网络中节点的度分布是判别研究网络是否为无标度网络的重要判据。节点度分布采用分布函数p(k)表示，指一个任意选择的节点恰好有k条边的概率，也等于网络中度数为k的节点的个数占网络节点总个数的比值。无标度网络的度分布为幂律分布，随机网络和小世界网络的度分布为指数分布[12]。

图3给出了该工业园共生网络的节点度数k的累积分布。在双对数坐标下，该工业网络的节点度数累积分布近似呈一条直线。采用最小二乘法得到其拟合曲线的表达式：

p(k)=0.3289k-0.9213

(1)

由此可知，该生态工业网络是无标度网络。这表明该网络中存在少量的Hubs节点(即度较大的节点)，这些节点在网络中占有主导地位，影响着园区内度相对较小的节点。同时，由于无标度网络具有“优先连接”的特性，因此园区新建的企业更倾向于和网络中的Hubs节点相连接，这种现象也称为“富者愈富”。

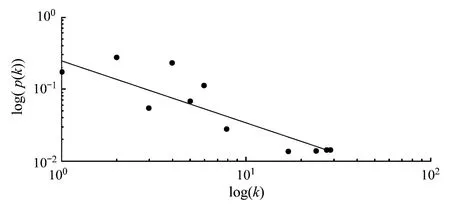
图3 生态工业网络的节点度数累积分布Fig.3 Cumulative degree distributions of the Eco-industrial networks

2.2 小世界性

有研究者通过对WS小世界网络的聚类系数和平均最短路径长度随重连概率p的变化关系的分析发现，小世界网络模型具有较短的平均路径长度和很高的聚类系数。Sporns等指出，当网络满足式(2)时，网络具有小世界特征[23]。

(2)

结果表明：该工业园的平均最短路径长度接近随机网络，聚类系数大于随机网络聚类系数，同时满足等式(2)，可判断该工业园共生网络具备小世界特征。同时由表1可知，工业园区网络的平均路径为3.6759，可认为连接两个节点之间的最短关系链中平均可通过3或4个企业将其连接，在实践中可理解为一部分企业节点之间可通过节点连接，一部分企业之间没有边连接，但有较小的平均路径；聚类系数为0.1235，可认为网络中两个节点之间有边连接的概率为12.35%，具有相对较高的聚类系数。网络聚类系数越大，表明工业网络中所有企业间能量/信息交流的越便捷，网络的集团化程度越高。

3 工业共生网络脆弱性分析

工业园在实践过程中，常表现出不稳定的现象，如工业共生网络组织成员之间共生关系减弱，特别当园区重要企业(或负载最大企业)发生故障时，共生网络的稳定性问题受到很大的威胁，严重的可能会导致整个共生链条上的企业生产运营陷于瘫痪。这使得工业共生网络中节点企业和工业园整体显示出某种程度的脆弱性。工业共生网络脆弱性以工业园复杂网络为载体，系统内部节点间交互关系具有复杂性。借鉴前人对系统脆弱性研究成果，本文给出工业共生网络脆弱性的定义如下：在生态工业园运行过程中，网络受到各种外界干扰所导致整个工业共生网络所表现出来的损失程度。因此，如何采用有效指标来测度生态工业园的脆弱性显得尤为重要。本文采用的案例是具有无标度性和小世界性的网络，该类网络具有hubs节点和较高的聚类系数，因此负载最大节点(企业)的安全性和稳定性对该网络的脆弱性有极大影响。本文从网络拓扑结构出发，在攻击负载最大节点条件下，利用网络效率和最大连通子图对该网络的脆弱性进行分析，从而衡量节点失效对整个网络造成的破坏性。

3.1 网络效率、节点负载和最大连通子图

网络效率是用来描述网络间信息传递能力的物理量。依据网络效率的评价结果，可尝试改善网络的拓扑结构进而优化网络效率，使网络具备抵御突发事件的能力，即使得网络弹性更强。Zhao等[24]提出了网络效率的定义，建立了一个网络模型如下：

G=(H,M)

(3)

式中，H是点集合，M是边集合。

(4)

式中，E(G)为网络效率，且0≤E(G)≤1，N为网络中节点数目，eij为节点i，j的连通效率，dij为节点i，j最短路径。

节点负载量对网络效率会有影响。这里引入节点负载和节点能力两个定义来进一步说明。网络中不相邻节点i和j之间的信息交换主要依赖于连接节点i和j的路径所经过的节点，如果某个节点被其他许多路径经过，则表示该节点在网络中的负载量很大。点介数可用来定量描述某个节点在网络中的负载量[27]，相应的计算见式(5):

(5)

式中，σij表示节点i和j之间最短路径的总数，σij(υ) 表示节点i和j之间最短路径经过节点v的数量，这里υ≠i,υ≠j,i≠j。

节点能力是指网络中某节点能处理的最大负载量。在实际网络中，节点能力受到成本的限制。假设节点v的能力和它的初始负载Bυ(0)成正比[28]，可表示为：

Aυ=(1+α)Bυ(0)

(6)

式中，Aυ为节点v能力，α为容忍参数，α在0—1之间取值。

最大连通子图是指将图中所有节点用最少的边连接起来的子图，即该子图内所包含的节点比网络中其它子图都要多，且任意两个节点之间都存在通路。有研究者表明一个网络总是存在一个最大连通子图[29]。网络中节点受到攻击后，网络遭受的破坏性采用最大连通子图规模S来衡量，具体的表达式为：

(7)

式中，N′为网络节点受到攻击后最大连通子图的节点数；N为网络中节点总数；在初始状态，最大连通子图规模S为1，表明初始网络是一个全连通无向图；当S为0时，网络几乎崩溃。因此，分析工业网络遭受攻击后的最大连通子图规模变化情况，对于研究工业共生网络的脆弱性具有重要意义。

3.2 工业共生网络脆弱性仿真分析

工业园共生网络作为一种典型的复杂网络，会面临两种攻击即随机攻击和蓄意(或选择性)攻击。假定当工业园中一个企业(节点)遭受到攻击时，与它所连接的边发生断裂，其负载量就在其临近的节点重分配，负载重分配有多种规则，这里根据发生故障节点的临近节点的负载比例来分配[28]。当临近节点新的负载量大于该节点能力时，也会发生故障，直到当节点新的负载量小于等于节点能力时，连锁故障结束。以往的研究表明，复杂网络对于随机攻击具有一定的鲁棒性，而对于蓄意攻击(如攻击负荷最大节点)是非常脆弱的[16, 26]，因此本文仅考虑蓄意攻击。特别需要说明的是，网络负载分为结构负载和实际的物理负载，在未确定网络实际物理负载的情况下，采用结构负载(由拓扑结构决定的负载)来研究复杂网络的脆弱性具有指导意义。本文采用点介数来代表结构负载。

3.2.1 网络效率变化

本文采用MATLAB7.0编程，得到该工业园区72个节点的负载排序(表2)。其中，污水处理厂(节点编号为32)负载最大。依次攻击生态工业网络负载最大的前20个节点，可得到网络效率的变化曲线(见图4)。由图4可知，当攻击负载最大的前4个节点(污水处理、废渣再利用、聚氯乙烯和废气余热回收)时，网络效率下降最快，随后网络效率下降速度变缓，当攻击到负载排序为第16节点(聚乙烯)时，网络效率基本保持不变。这说明在网络中，攻击负载最大的节点会使得网络效率急剧下降，网络弹性也变小，脆弱性增加。因此，在工业网络规划和建设中，保护具有较高介数的节点尤为重要，如污水处理厂发生故障不能运行时，工业园区的污水处理就存在很大问题，不但不能满足生态工业园的环境保护指标，而且危及周边群众的身体健康。

Kinney等以网络的平均效率用于衡量级联效应后的网络性能，对北美电网的结构脆弱性分析表明，基于最大介数的攻击带来的连锁故障后果相比随机攻击更加严重[30]。因此，这里引入容忍参数α，着重研究攻击网络中负载最大节点时，网络效率的变化趋势，以反映信息在工业共生网络中的传播情况。

表2 节点结构负载分布

结合生态工业园区自身特点，本文将α作为企业抵御故障能力的参数，受成本的影响。当α=0时，表示企业完全停产，无生产能力；当α=1时，表示企业受到攻击(或影响)后，在无成本约束下维修能保持大部分的生产能力；当α=0.3时，表示企业受到攻击(或影响)后，企业在维修成本约束下，能维持一定比例的生产能力。需要说明的是，当E为0时，表明网络中所有节点是孤立的。图5显示出不同容忍参数下网络效率的变化曲线。当α等于0时，介数最大的节点发生故障后网络的E降至最低，即为0.021。随着容忍参数α的增大(在0—1变化)，网络效率不断上升。当α等于1时，网络效率上升到0.0758。这表明该网络具有对选择攻击的脆弱性，当攻击介数最大的节点时，对工业共生网络的连通性有着极其重要的影响。在实际情况下，由于受成本的限制，α通常小于等于0.3。当α等于0.3时，网络效率E为0.0471。

结合本文实例分析，假如在该工业园区运行过程中，聚氯乙烯厂(节点负载排序第三)停产(α=0)，其原料供应企业如电石厂、热电厂将受到不同程度的影响，如果将该工业共生网络作为一个相对封闭的系统，由于电石厂生产的电石仅供聚氯乙烯厂使用，聚氯乙烯厂停产造成的负载部分转嫁给电石厂，从复杂网络理论的角度来理解就是电石厂新的负载量大于其能力(α=0)，那么电石厂也会导致停产；而热电厂由于生产的蒸汽供应的企业不止聚氯乙烯厂一家，热电厂生产能力受到影响(0<α<1)，可通过调整其运行负荷(最佳负荷)来适应外界的变化(如α=0.3)。因此，可理解为热电厂(节点)新的负载量小于该节点能力，因此不会发生故障。聚乙烯厂下游企业受到影响的程度也可按以上要求来分析。

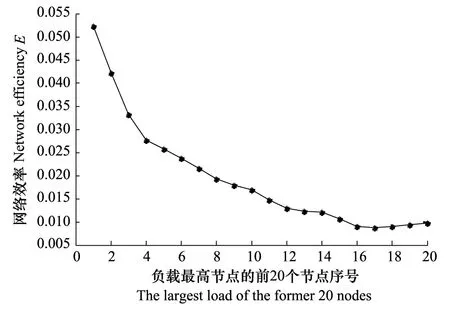
图4 依次攻击节点负载最高的前20个节点网络效率变化曲线Fig.4 The changing trend of network efficiency when attacking the node with larger load

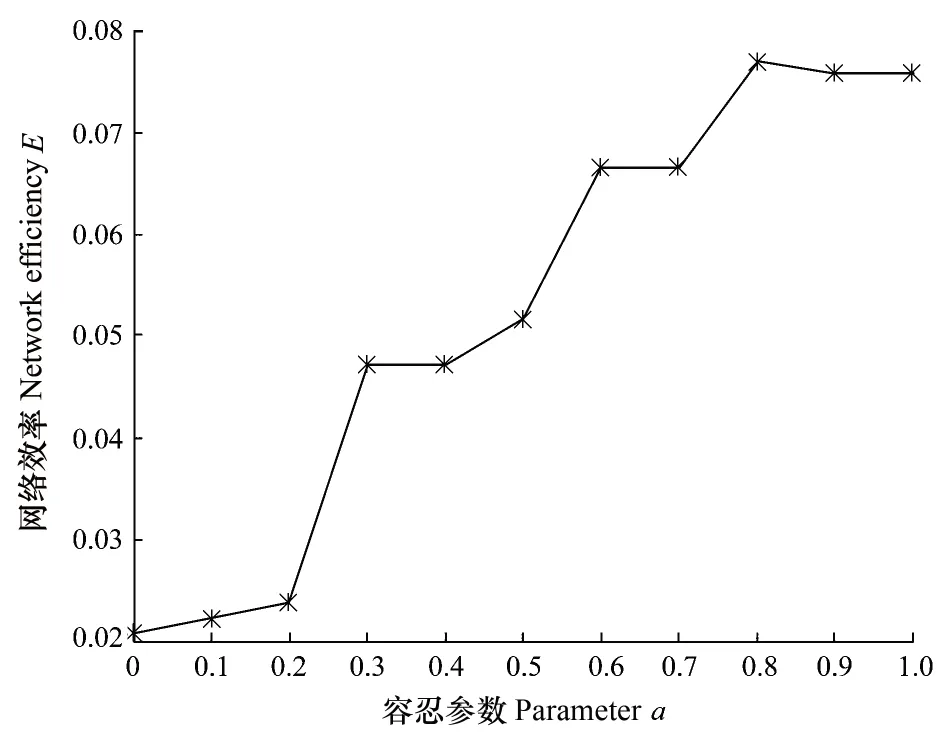
图5 不同容忍参数下的网络效率变化曲线Fig.5 Network efficiency versus tolerance parameter

3.2.2 最大连通子图规模

最大连通子图规模是衡量网络受破坏程度的物理量。由网络效率变化趋势可知，整个工业共生网络中，负载最大的节点遭受攻击后对网络的抗毁性和稳定性影响最大。因此，当采用最大连通子图规模衡量网络的脆弱性时，主要考虑攻击网络负载最大节点(节点编号为32)的情况，分析不同容忍参数下网络最大连通子图规模的变化情况(图6)。在α等于0时，介数最大的节点发生故障后网络的S降至最低，即为0.375。随着α的增加，S不断增大。当α等于1时，该网络的连通性仍然维持在较低水平，其S下降高达17%，这一数据低于无标度网络的20%[31]。这表明介数大的节点在网络中处于关键地位，对连锁故障的传播更为重要。实际情况下，由于成本的限制，α通常小于0.3，则最大连通子图规模一般小于0.65左右。这里还是以聚氯乙烯厂为例，当它发生停产时(α=0)，与其有关的企业受到不同程度影响，上游企业如电石厂将停产，那么电石厂与聚氯乙烯厂联系断裂，它们之间不存在连通；热电厂调整负荷仍能维持生产，与相关企业保持连通。下游企业如烧碱厂、有机硅厂、波纹管厂等由于将聚氯乙烯厂产品作为生产原料，这些下游企业面临停产，与聚氯乙烯厂联系断裂，它们之间均不存在连通。可见，在此条件下，最大连通子图规模会降到最低。当聚氯乙烯厂维修能保持大部分的生产能力时(α=1)，由于上下游企业与其联系紧密程度不同，受到的影响程度不同，一般联系最紧密且经济效益较小的企业发生断链的可能性最大。对应的最大连通子图规模也会受到影响。

图6 不同容忍参数下的最大连通子图规模Fig.6 The size of The largest connected facts component versus tolerance parameter

从不同容忍参数下的网络效率和最大连通子图规模变化曲线可看出，容忍参数α为0—0.3时，网络效率和最大连通子图表现出急剧的变化趋势。这表明网络在遭受蓄意攻击即攻击负载最大节点时，工业共生网络的拓扑结构发生剧烈变化，容易造成园区物质流、能量流的断裂，导致“孤立”企业的产生，从而使得工业园抵御风险的能力下降。

4 结论与讨论

工业共生网络是生态工业园内企业生态合作的主要组织形式，是生态工业园建设过程中的核心内容。共生网络能否稳定安全运行直接关系到生态工业园的成败。本文运用Ucinet6.0和MATLAB7.0软件，利用复杂网络理论构建了某化工工业园共生网络的拓扑结构，对其基本拓扑性质进行了分析，结果表明该生态工业园具有无标度和小世界特征。同时，利用节点负载(节点介数)、网络效率和最大连通子图规模对该工业共生网络的脆弱性进行了研究，依次攻击负载较大节点，网络效率呈下降趋势；同时容忍参数为0—0.3时，网络效率和最大连通子图表现出急剧的变化趋势。网络中负载最大节点受到攻击时，工业共生网络的拓扑结构发生剧烈变化，容易造成园区物质流、能量流的断裂，工业园抵御风险的能力下降。

目前，研究者已逐步开始关注复杂网络受到攻击的问题，其目的在于确定现实生活中网络的鲁棒性和脆弱性，这对于实际运用中保护许多基础设施网络如电力网络，或破坏谣言的传播和控制疾病的流行等方面是非常重要的。生态工业园由于园区中各企业扮演的角色不同，相应各企业的地位也不同，同时园区存在物质流、能量流和信息流，是一个典型的复杂网络。本文的研究工作对于有效保护关键节点，确保工业共生网络的稳定安全运行，从而避免级联效应带来的灾害等方面具有重要的实际意义。下一步的工作需要进一步模拟实际工业园区的真实过程，将工业园作为有向、有权网络来分析，同时如何使研究涉及的参数在生态工业园共生网络的运行中发挥作用，降低网络的脆弱性，进一步提高工业生态网络的稳定性和可靠性，也将是进一步研究的内容。

[1] Chertow M R. Industrial symbiosis: literature and taxonomy. Annual Review of Energy and the Environment, 2000, 25(1): 313- 337.

[2] Mirata M, Emtairah T. Industrial symbiosis networks and the contribution to environmental innovation: The case of the Landskrona industrial symbiosis programme. Journal of Cleaner Production, 2005, 13(10/11): 993- 1002.

[3] Li X P. Study on the Stability and Eco-efficiency Assessment of the Industrial Symbiosis Network in Eco-industrial Park [D]. Tianjin: Tianjin University, 2011.

[4] Wu C Y, Deng H, Duan N. Review on the study of the stability of industrial ecosystem. China Population, Resources and Environment, 2005, 15(5): 20- 25.

[5] Tan R R, Col-long K J, Foo D C Y, Hul S, Ng D K S. A methodology for the design of efficient resource conservation networks using adaptive swarm intelligence. Journal of Cleaner Production, 2008, 16(7): 822- 832.

[6] Yuan Z W, Bi J. Evolution mechanism of eco-industrial symbiosis network and its analytical framework. Acta Ecologica Sinica, 2007, 27(8): 3182- 3188.

[7] Wang Z H. Industrial Symbiotic Network of Eco-industrial Parks [D]. Dalian: Dalian University of Science and Technology, 2002.

[8] Deng H. Research on the Influence Factors of Industrial Ecosystem (IES) Stability in China [D]. Dalian: Dalian University of Science and Technology, 2006.

[9] Luo L H. Research on the System Stability and Control of Eco-industrial Park [D]. Beijing: Beijing Forestry University, 2011.

[10] Li Y. Research on Growth Mechanism of Eco-industrial Symbiosis Network in Complex Network Perspective [D]. Tianjin: Tianjin University of technology. 2012.

[11] Watts D J, Strogatz S H. Collective dynamics of ‘small-world’ networks. Nature, 1998, 393(6684): 440- 442.

[12] Barabási A L, Albert R. Emergence of scaling in random networks. Science, 1999, 286(5439): 509- 512.

[13] Yang L H, Tong L J. Research of typical EIPs based on the social network analysis. Acta Ecologica Sinica, 2012, 32(13): 4236- 4245.

[14] Xiao Z D, Zha Z P, Xu C. Application research on complex network of industrial ecological system. Systems Engineering, 2010, 28(5): 58- 63.

[15] Song Y M, Shi L. Complexity measurements for Kalundborg and Gongyi industrial symbiosis networks. Journal of Tsinghua University: Science and Technology, 2008, 48(9): 1441- 1444.

[16] Zhang J H. The Research on Connectivity Vulnerability of Metro Complex Networks [D]. Wuhan: Huazhong University of Science and Technology, 2012.

[17] Chinese Ministry of Environmental Protection. HJ/T 409—2007. Guide for Established of Eco-industrial Parks Planning. Beijing: China Standard Press, 2007.

[18] Strogatz S H. Exploring complex networks. Nature, 2001, 410(6825): 268- 276.

[19] Lowe E A, Moran S R, Holmes D B. Eco-industrial Parks: a Handbook for Local Development Teams. Oakland, CA: Indigo Development, RPP International, 1998.

[20] Costa L da F, Rodriguesa F A, Traviesoa G, Villas Boas P R. Characterization of complex networks: A survey of measurements. Advances in Physics, 2007, 56(1): 167- 242.

[21] Ehrenfeld J, Gertler N. Industrial ecology in practice: the evolution of interdependence at Kalundborg. Journal of Industrial Ecology, 1997, 1(1): 67- 79.

[22] Watts D J. Networks, dynamics, and the small-world phenomenon. American Journal of Sociology, 1999, 105(2): 493- 527.

[23] Sporns O, Honey C J, Kötter R. Identification and classification of hubs in brain networks. PLoS ONE, 2007, 2(10): e1049.

[24] Zhao L, Park K, Lai Y C. Attack vulnerability of scale-free networks due to cascading breakdown. Physical Review E, 2001, 70(3): 5101- 5114.

[25] Cohen R, Erez K, Ben-Avraham D, Havlin S. Resilience of the internet to random breakdowns. Physical Review Letters, 2000, 85(21): 4626- 4628.

[26] Cohen R, Erez K, Ben-Avraham D, Havlin S. Breakdown of the internet under intentional attack. Physical Review Letters, 2001, 86(16): 3682- 3685.

[27] Freeman L C. A set of measures of centrality based on betweenness. Sociometry, 1977, 40(1): 35- 41.

[28] Wang J W, Rong L L. Cascade-based attack vulnerability on the US power grid. Safety Science, 2009, 47(10): 1332- 1336.

[29] Bao Z J, Cao Y J, Ding L J, Wang G Z, Han Z X. Synergetic behavior in the cascading failure propagation of scale-free coupled map lattices. Physics A: Statistical Mechanics and its Applications, 2008, 387(23): 5922- 5929.

[30] Kinney R, Crucitti P, Albert R, Latora V. Modeling cascading failures in the North American power grid. The European Physical Journal B, 2005, 46(1): 101- 107.

[31] Motter A E, Lai Y C. Cascade-based attacks on complex networks. Physical Review E, 2002, 66(2): 065102- 1- 3, doi: 10.1103/PhysRevE.66.065102.

参考文献:

[3] 李小鹏. 生态工业园产业共生网络稳定性及生态效率评价研究 [D]. 天津: 天津大学, 2011.

[4] 武春友, 邓华, 段宁. 产业生态系统稳定性研究述评. 中国人口·资源与环境, 2005, 15(5): 20- 25.

[6] 袁增伟, 毕军. 生态产业共生网络形成机理及其系统解析框架. 生态学报, 2007, 27(8): 3182- 3188.

[7] 王兆华. 生态工业园工业共生网络研究 [D]. 大连: 大连理工大学, 2002.

[8] 邓华. 我国产业生态系统(IES)稳定性影响因素研究 [D]. 大连: 大连理工大学, 2006.

[9] 罗柳红. 生态工业园区系统稳定性与调控研究 [D]. 北京: 北京林业大学, 2011.

[10] 李勇. 复杂网络视角下的生态产业共生网络成长机制研究 [D]. 天津: 天津理工大学, 2012.

[13] 杨丽花, 佟连军. 基于社会网络分析法的生态工业园典型案例研究. 生态学报, 2012, 32(13): 4236- 4245.

[14] 肖忠东, 查仲朋, 徐琛. 复杂网络理论在生态工业系统的应用研究. 系统工程, 2010, 28(5): 58- 63.

[15] 宋雨萌, 石磊. 工业共生网络的复杂性度量及案例分析. 清华大学学报: 自然科学版, 2008, 48(9): 1441- 1444.

[16] 张建华. 地铁复杂网络的连通脆弱性研究 [D]. 武汉: 华中科技大学, 2012.

[17] 中国环境保护局. HJ/T 409—2007. 生态工业园区建设规划编制指南. 北京: 中国标准出版社, 2007.

Vulnerability analysis of symbiotic network in Eco-industrial parks

LI Xiangmei1,*, XIAO Renbin2, ZENG Yu2, YAO Zhishuang3

1HubeiUniversityofEconomics,Wuhan430205,China2InstituteofSystemsEngineering,HuazhongUniversityofScienceandTechnology,Wuhan430074,China3WenhuaCollege,HuazhongUniversityofScienceandTechnology,Wuhan430074,China

The idea of eco-industrial parks (EIPs) is a new industrial organization form that reconciles the three dimensions of sustainability: society, economy and environment. EIPs represent a practical way to apply the concept of industrial symbiosis (IS). Industrial Symbiosis Network (ISN) is a complex system consisting of a variety of enterprises and embedded relations. The keys of ISN are collaboration and synergistic possibilities offered by geographic proximity. Since the 1970s, the EIPs practice is conducted in many countries, i.e., Denmark, USA, Australia, Japan, and China and so on. However, many factors such as technological innovation, combination, takeovers and so on have a great negative influence on the practice of EIPs. Therefore, it is very important to make scientific analysis of the vulnerability of EIPs, thus providing effective measures to develop ISN. This paper employs the complex network theory to analyze the statistical properties of symbiotic network in EIPs. The nodes in EIPs represent the enterprises, and the edges between the nodes denote the symbiosis relationships. So the complex network theory is supposed to be effective in describing the real ecological industrial system. The complex characteristics of industrial symbiosis network are analyzed from three aspects: (1) The enterprises in EIPs form industrial ecological chains networks involving horizontal and vertical coupling; (2) The diversity of the enterprises made the node complexity; (3) The ISN is affected by a wide variety of factors. After describing the case of certain coal chemical eco-industrial park (abbreviated as CCEIP hereafter), we establish the topology of the EIP by employing the NetDraw tool of Ucinet (version 6.0) software. The statistical characteristics of the network in CCEIP are then examined. An index system including degree, degree distribution, clustering coefficient, average shortest distance length is developed to measure the topological properties. Results show that CCEIP′s average shortest distance length (3.6759) and clustering coefficient (0.1235) are both higher than those of random network (2.6780 and 0.0686 respectively). The degree follows power-law distribution. Therefore, we can infer that CCEIP has the small world and scale-free characteristics. As the security and stability of the nodes with maximum load greatly affects the network vulnerability, the paper adopted a strategy of deliberately attacking the nodes with maximum load, such as the anthropogenic bankruptcy of enterprise. Two important indexes, the network efficiency and the largest connected component, were used to analyze the network vulnerability and to measure the damage degree of cascading failure. The network efficiency declines tendency when the nodes of larger load are attacked. When the tolerance parameter is in the range of 0—0.3, the network efficiency and the largest connected component change abruptly.

Eco-industrial parks; symbiotic network; vulnerability; topological characters

国家自然科学基金资助项目(71171089); 湖北省自然科学基金资助项目(2012FFB02702)

2012- 12- 19; 网络出版日期:2014- 03- 04

10.5846/stxb201212191820

*通讯作者Corresponding author.E-mail: xmlihust@aliyun.com

李湘梅, 肖人彬, 曾宇, 姚智爽. 生态工业园共生网络的脆弱性. 生态学报, 2014,34(16):4746- 4755.

Li X M, Xiao R B, Zeng Y, Yao Z S. Vulnerability analysis of symbiotic network in Eco-industrial parks.Acta Ecologica Sinica,2014,34(16):4746- 4755.