最小支撑树混合贪婪算法求解车辆路径问题

张 恒，冉 雨，于卓岑，俸 卫*

(1.内江师范学院数学与信息科学学院，四川内江641100； 2.内江师范学院四川省高等学校数值仿真重点实验室，四川内江641100)

物资配送［1］是物资流通企业按照用户的订货需求及其标准，以最经济的方式对货物进行采购、储存、加工、分拣、配装、运输，直到把货物交到用户手中的物资流通活动.由于物流对国民经济的重大影响，物流系统化、合理化能创造巨大经济利益，因此物流与商流、信息流并称为现代经济的三大支柱，被称为继劳动力、资源之后的“第三大利润源泉”［2］.而如今，物流企业面临的现状是服务效率较低，服务成本较高.

现阶段，国内外对物资配送的研究主要涉及车辆调度，路径优化方面的研究，并针对不同问题采用各种算法进行求解［3-4］.C.Clarke 等［5］在 1964年针对车辆调度问题首先提出C-W节约启发式算法，其算法具有较强的局部搜索能力.王刚［6］利用遗传算法全局搜索能力的特点研究车辆调度问题.最近，喻伟等［7］将遗传算法的全局搜索能力与节约算法的局部搜索能力相结合，设计了遗传节约综合算法.而现代物流不仅要降低成本，更要满足客户的需求，因此如何在满足用户需要的前提下，进一步降低物流成本已成为国内外许多理论与应用学者研究的焦点.

文章将针对一定客户规模的物资配送进行研究，建立区域划分——路径优化模型，设计最小支撑树混合贪婪算法求解.最终达到物流企业物资配送低成本，高效率的目的.

1 问题描述

物资配送问题的一般描述为:某配送中心拥有一支货运车队，为若干个客户配送物资，配送中心与客户以及客户与客户之间的公路里程为已知.配送中心如何制定每天的配送方案?配送方案包括:当天出动的车辆数，出行时间，行驶路径等，由此形成当天的总运行里程.一个合格的配送方案要求配送中心按照客户需求，高效率为客户服务；而一个好的配送方案还应该给出使配送费用最小或总运行里程最短的车辆调度方案，降低配送中心的服务成本.

2 车辆路线问题的数学模型

车辆路线问题假设如下:

1)有相同载重量Q的车m辆；

2)只有一个配送中心，并以配送中心为路线的起止点；

3)有l个客户且每个客户在不同的地理位置；

4)每个客户都有一个确定的需求量di，且每个客户有且只有被其中一辆车满足；

5)每个客户有且只被服务一次；

6)每辆车必须服务若干客户，且始于配送中心，终于配送中心；

7)对被一辆车所服务的客户集的总需求量不超过车辆的载重量.

目标为每辆车设计一条路线，使得总运输里程最小，并且确保全部客户的需求得到满足.定义0-1决策变量:

假设z为k个客户集的总运输里程，车辆路线问题的模型［8］如下:

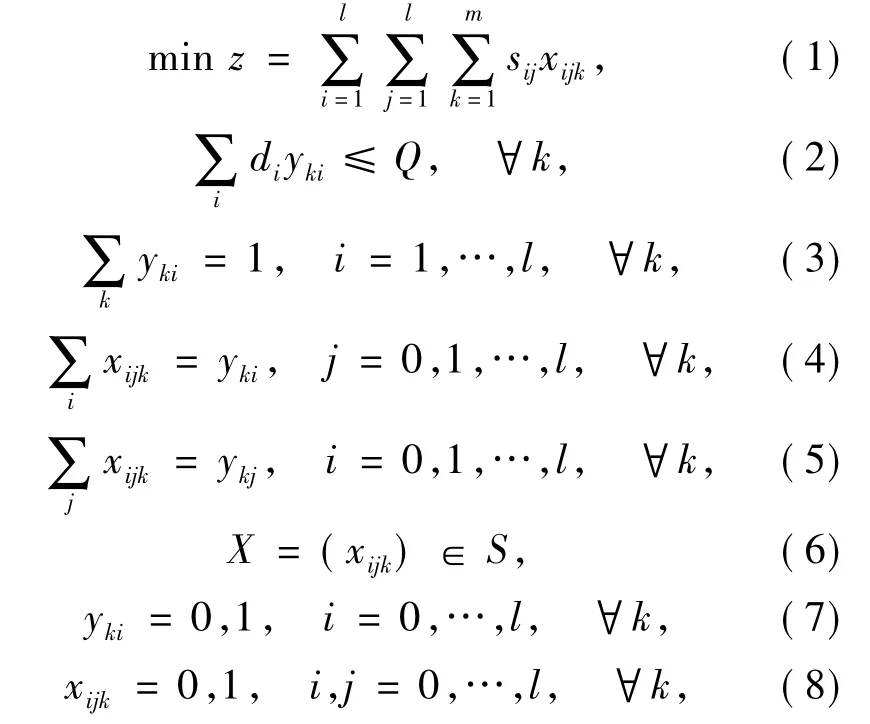
模型中各式含义如下:(1)式为目标函数，表示k个客户集总的最小运输成本，l为客户数，m为最大车辆估计数(通过文献［4］可确定)，sij代表客户i到客户j的距离.(2)式为载重约束，表示第k个客户集里的客户总需求量不超过一辆车的载重量.(3)式表示客户集中每个客户都只被车辆k服务一次.(4)～(5)式表示所有车辆起于点i，终于点i.(6)式保证巡回路线不出现子圈.(7)～(8)式为变量约束.

在配送中心和客户之间的车辆调度问题的客户规模和约束条件较少时，可精确求解.但经考察发现，现实中物流公司物资配送服务的客户数量较大(客户数量级≥102).在这种大规模条件下，直接求解难度较大，难以运用到实际生活中［9］.因此，本文思路利用最小支撑树算法对客户先进行区域划分，缩小问题规模，再用贪婪算法对每个分区求解最优路线.

3 最小支撑树混合贪婪算法

3.1 区域划分问题描述以及数学模型区域划分假设如下:区域中有一个配送中心；每个客户都要被服务；一辆车服务于一个分区，且一个分区仅有一辆车服务.目标是将客户分成若干个客户集，使得配送中心到客户集，客户集中客户与客户的距离总和最小，且保证每个分区内的总需求量不超过一辆车的最大载重量.区域划分的目的是分解规模，方便优化和计算，而且也是管理本身的需要.定义0-1决策变量:

建立区域划分的数学模型［10］如下所示:

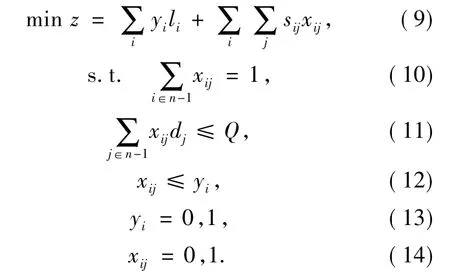
根据后文案例，该模型通过Lingo软件也可以实现.模型中各式含义如下:(9)式为目标函数，使得运输成本最小化.li表示第i分区中，距离配送中心最近的客户点到配送中心的运输里程，sij表示节点j到本分区距离配送中心最近的客户点的运输成本.(10)式表示每一客户点都被选中.(11)式表示每一分区内的需求总量不超过单辆车的载重量，dj为第j个客户所需物资的重量，Q为单辆货车载重量.(12)式表示分区i与客户点j的关系.(13)～(14)式为变量约束.

3.2 基于最小支撑树的区域划分算法设G=(V，E，w)是一个连通赋权图，顶点个数为n，T是G的一棵生成树，T的每条边所赋权之和称为T的权，记为W(T).G中具有最小权的生成树称为G的最小支撑树［11］.求最小支撑树的Prim算法(反圈法)如下所述:

Step 1在连通赋权图G中取一顶点v1相关联的且权值最小的边，设为e(v1v2)；

Step 2在边集{e(v1v2)|1≤i≤2，v∉{v1，v2}}中选取一条权值最小的边记为e(viv3)；

Step 3假如已找到p个顶点v1，v2，…，vp，在边集{e(v1v)|1≤i≤p，v∉{v1，v2，…，vp}}中选取一条权值最小的边记为e(vivp+1)，如果已经选出n-1条边，则所有选出的边在图G中构成的子图即为G的一棵最小支撑树.

根据文献［11］基于最小支撑树的通用区域划分算法描述，首先实现配送区域划分，划分示意图如图1所示.

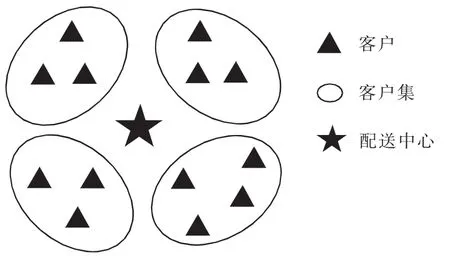
图1 区域划分示意图Fig.1 Schematic diagram of regional division

物资配送是物流的关键环节，其中物流公司如何安排车辆的行驶方案，直接影响到物流公司的运输成本.因此，在配送区域确定后，需要确定的是各区域中车辆的行驶路径，进而得到优化的车辆路径方案.

3.3 贪婪算法求单车辆路径问题本文设计相对于TSP问题的贪婪算法(TSPGEA)［12］，令K表示顶点集为V(K)、弧度集A(K)的完全图(如果x和y是K中的顶点，那么xy，yx∈A(K)，|V(K)|=n).对于K中的任意弧度xy被分派为一个实数值C(xy)=CK(xy).用C(K)代表K中弧度值的和，结合递归程序TSPGEA(n，K，C(K))计算C(K)，在K中找到一个最小值的哈密尔顿巡回路线.TSPGEA(n，K，C(K))程序步骤:

Step 1如果n=2，得到K回路；

Step 2计算∀x∈V(K)，C+(x)和C-(x)，这里

Step 3∀b∈A(K)，用(C(K/xy)=C(K)-C+(x)-C-(y)+C(xy)-c(yx))计算C(K/b)；

Step 4在K中寻找a(a=xy)，使得τa(K)=min{τuw:u(K)≠w∈V(K)}；

Step 5计算T=TSPGEA(n-1，K/a，C(K/a))；

Step 6用T代替弧度为a的顶点va；

Step 7返回T.

4 实例分析

为了测试算法的有效性，运用以上算法流程，求解如下问题:现有一批物资配送任务，送货车辆从配送中心(i=0，坐标为原点)出发，为编号是i=1，2，…，8的8个客户配送物资.其中货车载重量为Q=200个单位、平均速度为v=50 km/h，某天，第i个客户所需物资的重量为qi个单位(qi＜Q)，如表1.

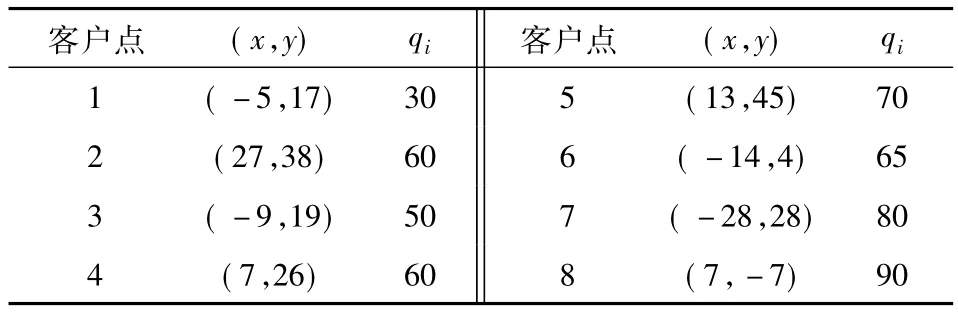
表1 客户点坐标及需求量Table 1 Customer point coordinates and demand

在内存为4 GB，CPU速度为1.80 GHz的硬件环境下，使用Windows 7操作系统，利用Matlab 7.0编程求解［13］.结合最小支撑树的区域划分算法的设计步骤，求解过程耗时0.001 054 s，得到车辆分区方案:客户集1、2、3 的客户分别为2，4，5、1，3，7、6，8.

对于区域中路线的确定，结合贪婪算法的设计步骤，求解过程耗时0.014 865 s，最终得到车辆安排方案，见表2.

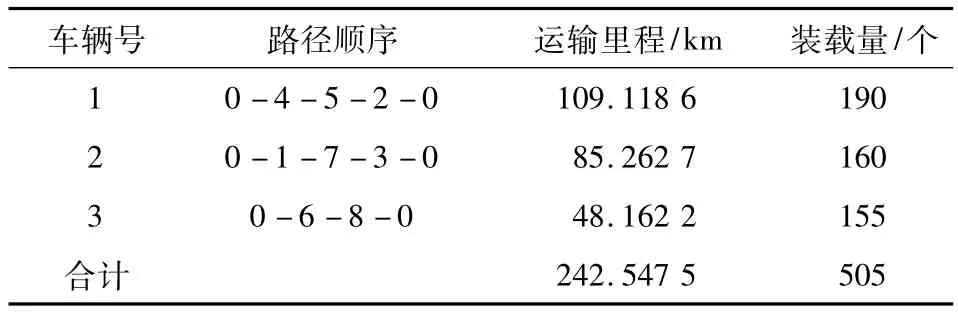
表2 车辆安排方案Table 2 Vehicle scheme of arrangement

根据上述结果分析，本问题算法求解耗时0.015 919 s，计算复杂度为n3，最优值为242.547 5 km.通过利用 Lingo软件编程求解［14］耗时8 s，得到分区结果一致，运输里程最优值为240.098 7 km，结果相差不大.但算法计算速度是Lingo的500多倍，说明本文设计的最小支撑树与贪婪算法的混合算法求解结果准确，计算速度快.同时通过与文献［15］中四叉树混合蚁群算法所得最优值248 km进行比较，结果更加优异，达到了运输成本更低的目的，说明了本文算法的有效性.

［1］陈会明.再论物资配送［J］.铁道物资科学管理，1997，4(15):9-10.

［2］林慧丹.第三方物流［M］.上海:上海财经大学出版社，2005:101-107.

［3］Homberger J，Gehring H.A two-phase hybird evolution metaheuristics for the vehicle routing with time windows［J］.European J Oper Research，2005，162(1):220-238.

［4］李军，郭耀煌.物流配送车辆优化调度理论与方法［M］.北京:中国物资出版社，2001.

［5］Clark G，Wright J.Scheduling of vehicles from a central depot to a number of delivery points［J］.Opens Res，1964，4.

［6］王刚.遗传算法在VRP中的应用与研究［D］.重庆:重庆交通大学，2011.

［7］喻伟，何其超，张增桀.遗传节约综合算法在配送路线优化中的应用［J］.物流科技，2009，3:49-52.

［8］郎茂祥.配送车辆优化调度模型与算法［M］.北京:电子工业出版社，2009.

［9］池洁.物流配送区域划分模型及优化计算研究［D］.重庆:重庆交通大学，2009.

［10］霍亮，安敏，李欣.一种城市物流分区配送方法的研究［J］.物流技术，2003，3:91-94.

［11］王玲娜，李兴明.基于最小支撑树的通用区域划分算法［C］//2008年中国西部青年通信学术会议论文集，2008.

［12］Gutin G，Yeo A.Polynomial approximation algorithms for the TSP and the QAP with a factorial domination number［J］.Discrete Appl Math，2002，119:107-116.

［13］孙祥，徐刘美，吴清.Matlab 7.0基础教程［M］.北京:清华大学出版社，2006.

［14］汪晓银，邹庭荣.数学软件与数学实验［M］.北京:科学出版社，2008.

［15］许菁，雷定猷，邓煜阳.基于区位理论的物流配送中心调度优化算法［J］.现代物流，2007，9:1-3.