基于DTC-SVM的多电机并联驱动系统*

马秀娟， 孙 洋， 张华强， 刘陵顺

(1. 哈尔滨工业大学(威海) 电气工程系，山东 威海 264209； 2. 海军航空工程学院 控制工程系，山东 烟台 264001)

0 引 言

多电机并联驱动系统不仅需要某个电机达到较高转速，而且需要多个电机能够协调运行。这对电机的调速性能提出了较高要求[1-2]。本文分析了基于空间矢量调制的直接转矩控制策略(Direct Torque Control with Space Vector Modulation， DTC-SVM)，并将该策略应用于多电机并联驱动系统中，依据多电机并联参数的平均化理论，提出一种基于DTC-SVM的多电机并联驱动方案，并进行了仿真验证。

1 空间矢量调制的直接转矩控制策略

空间矢量脉宽调制(Space Vector Pulse Width Modulation， SVPWM)技术成熟、应用广泛，其参考电压由空间电压矢量Uref给定，依据空间电压矢量切换对变流器进行控制。

传统直接转矩控制是通过查询开关表的方式来选择合适的电压矢量，使用两个滞环比较器来实现磁链和转矩的直接控制[3]。由于滞环比较器自身的原因，采用该控制策略易导致电流谐波大、转矩脉动大、逆变器开关频率不恒定。为解决该问题，采用PI调节器代替滞环比较器，应用SVPWM技术，用两个PI调节器分别对定子磁链和电磁转矩进行控制，动态响应快、转矩脉动小、输出波形连续平滑，获得较好的动、静态性能[4]。

空间矢量调制的直接转矩控制方案结构如图1所示。其中，磁链和转矩均采用闭环控制。由参考电压矢量Uref的分量Usx、Usy，定子磁链Ψs及电磁转矩Te，得到驱动逆变器开关管的开关信号SA、SB、SC。

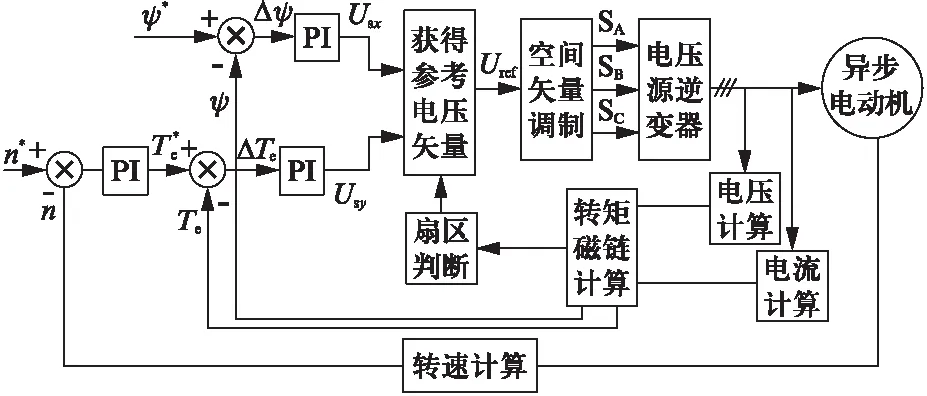
图1 空间矢量调制的直接转矩控制方案结构

该方案将检测到的逆变器输出电压和电流变换到αβ坐标系，然后计算出定子磁链Ψs、电磁转矩Te，并分别与参考给定磁链Ψ*、给定转矩Te*相比较，比较后的误差信号分别送入磁链、转矩PI调节器，得到参考电压矢量在定子磁链定向坐标系xy下的分量。经过SVPWM技术，最终产生驱动逆变器运行的开关信号。

2 多电机并联的直接转矩控制

2.1 多电机并联控制的数学模型

多电机并联驱动系统中，各异步电机由于工作状态不同，以及所带的负载有所差异，虽接受来自同一个逆变器所产生的电压空间矢量，但是各电机的电流也不尽相同。为实现协调控制，必须建立多电机并联的电流数学模型[5]，平均电流表达式为

(1)

另有

(2)

由式(1)和式(2)得各电机定子电流为

(3)

类似电流的平均化模型，对磁链进行平均化处理[6]。方案采用矢量平均化方法。

单电机定子磁链方程为

(4)

则多电机定子平均磁链方程为

其中，

(6)

单电机转子磁链方程为

将式(7)改写为

(8)

式中：A——转子参数，A=SrM；

M——互感，M=Lm；

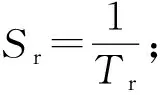
Tr——转子时间常数。

多台异步电机的平均转子磁链可通过各异步电机的转子磁链平均值和差值得到[7]。电机转子磁链矢量图如图2所示。

图2 电机转子磁链矢量图

根据矢量平均化方法，得到电机转子磁链方程为

(9)

ΔΨrn——各异步电机转子磁链差值；

Δωrn——各异步电机的转子角速度差值。

对于转矩的确定，可从每台电机的转矩算式出发，根据平均化思想，将各异步电机的转矩算式进行累加，通过转子磁链的平均值和差值及定子电流的平均值和差值，计算平均转矩[8]。转矩计算式为

ΔΨr2ΔIs2+…+ΔΨrnΔIsn)]

(10)

2.2 基于DTC-SVM的多电机并联驱动系统

在直接转矩控制的多电机并联驱动系统中，由于多台异步电机的工作状态、负载及损耗均不同，因此采用平均化理论，将多台异步电机拟合为一台“平均电机”进行控制。根据反向推导式，当出现乘积平均时，平均化理论需要利用差值算式，即

精确计算磁链和转矩是实现直接转矩控制的基础，将计算结果反馈到对应的磁链和转矩PI调

(11)

节器，结合磁链位置检测来确定逆变器输出的电压矢量。因此，为了实现基于空间矢量调制的直接转矩控制的多电机并联驱动系统，必须利用平均化理论计算多台异步电机的磁链和转矩，以此抽象出“平均电机”的定子磁链和转矩。

在两相静止坐标系下，定子磁链的计算可以采用电压模型，即

(12)

在多电机并联驱动系统中，利用差值算式对式(12)变量进行平均化处理，得

由于是多电机并联驱动系统，us均相等。若各台异步电机的参数和转速无差异，即可将多台异步电机当作单台异步电机进行控制。

对多电机的平均转矩，同样可模仿“平均电机”的磁链计算过程。从单电机的转矩算式出发，采用平均化思想，把各个异步电机的转矩算式累加，然后利用定子磁链的平均值和差值，以及定子电流的平均值和差值，计算出平均转矩。通过叠加，由单电机转矩算式引出多电机的平均转矩算式为

ΔΨsα2Δisβ2-ΔΨsβ2Δisα2+…+

ΔΨsαnΔisβn-ΔΨsβnΔisαn)

(15)

平均转速可表示为

(16)

通过计算得到平均化电机的各参数，基于DTC-SVM的多电机并联控制策略，计算平均化电机的各个参数，将得到的磁链和转矩分别反馈至相对应的PI调节器，其输出值经坐标变换，得到期望的逆变器输出电压矢量。多电机并联的DTC-SVM控制方案结构框图如图3所示。

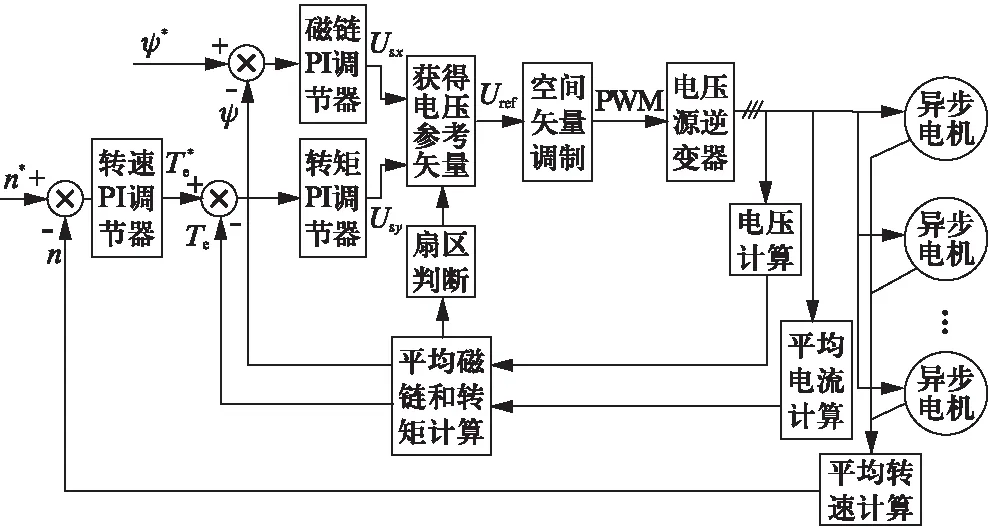
图3 多电机并联的DTC-SVM控制方案结构框图

3 仿真研究

3.1 基于DTC-SVM的单电机控制系统仿真研究

利用MATLAB/Simulink仿真工具，建立单电机控制系统仿真模型。仿真模型电机参数[4]： 额定功率2.2kW，额定电压380V，额定频率50Hz，给定转速1400r/min，PWM调制频率5kHz。仿真结果如图4、图5所示。

图4 DTC-SVM控制的起动转速、转矩波形

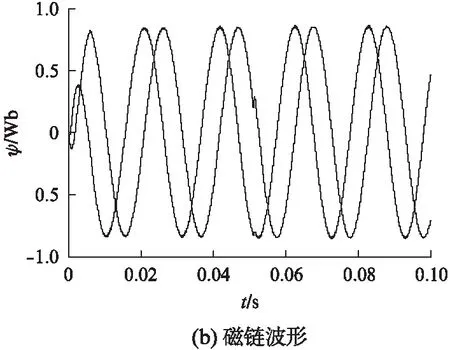
图5 DTC-SVM控制的磁链轨迹与波形

DTC-SVM控制的起动转速波形如图4(a)所示。由图可知，其特点是转速响应快、超调量小、稳态运行无静差。DTC-SVM控制的的转矩波形如图4(b)所示。由图可知，起动转矩大，稳态转矩波动较小，稳态时转矩波形平滑。

DTC-SVM控制的磁链轨迹如图5(a)所示，磁链轨迹是平滑的圆形轨迹。DTC-SVM控制的磁链波形为标准的正弦波，如图5(b)所示，可知其波形平滑。

3.2 基于DTC-SVM的多电机并联系统仿真研究

根据多电机并联驱动的平均化原理，多电机的平均转速、电流、磁链均可算出。利用MATLAB/Simulink仿真工具，建立仿真模型。

在单电机矢量调制直接转矩控制的基础上，加入多电机并联控制方案，利用平均模块将其模拟成一个“平均电机”。设用3台电机并联模拟为1台“平均电机”模型，单台电机参数[6]： 电机额定功率1kW，额定电压380V，额定转速10000r/min，电机给定转速8500r/min，PWM调制频率10kHz。仿真结果如图6～图8所示。

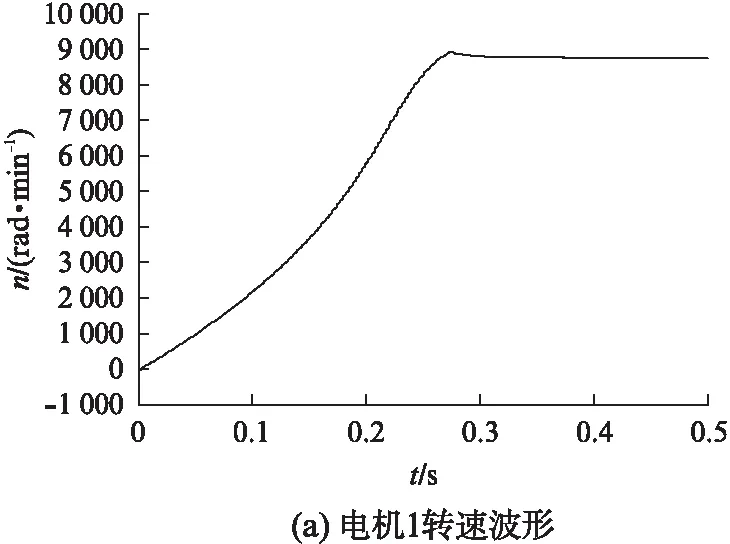
图6 3台电机并联起动转速波形

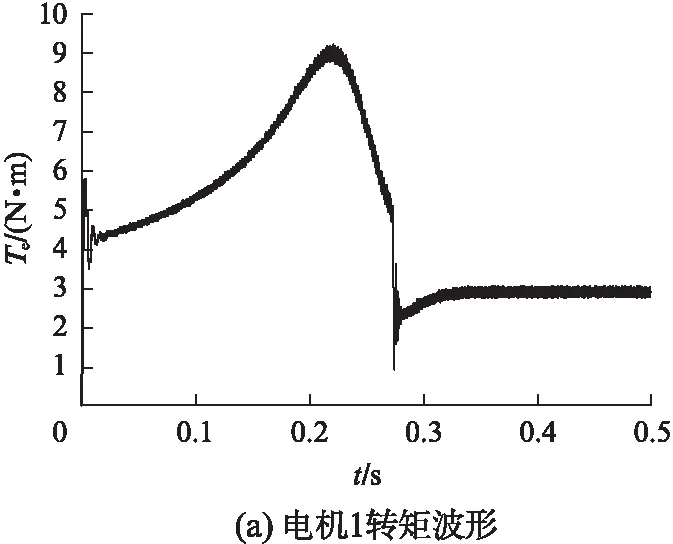
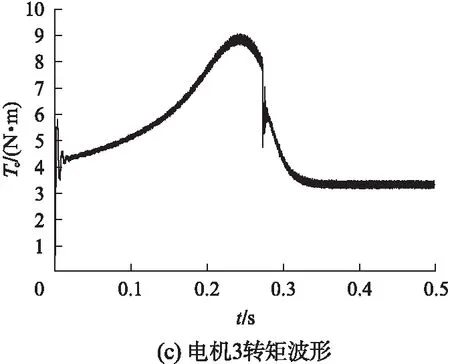
图7 3台并联电机起动转矩波形

并联电机各自的转速起动波形如图6所示。由图可知，电机转速响应快，电机1和电机2转速略有超调，但在误差允许范围内。延长起动时间，可有效减小转速超调。3台电机各自的给定转矩均不同，但其稳态转速仍能达到给定要求。

3台电机给定的转矩分别为2、1.6、2.4N·m。由图7知，3台电机的起动转矩较大，稳态转矩平稳，波动较小。

“平均电机”的磁链轨迹、“平均电机”的磁链波形分别如图8(a)、图8(b)所示。虽然逆变器输出驱动3台电机，但通过3台电机的平均矢量运算，其平均磁链波形仍为平滑的正弦波，磁链轨迹是平滑的圆形轨迹。

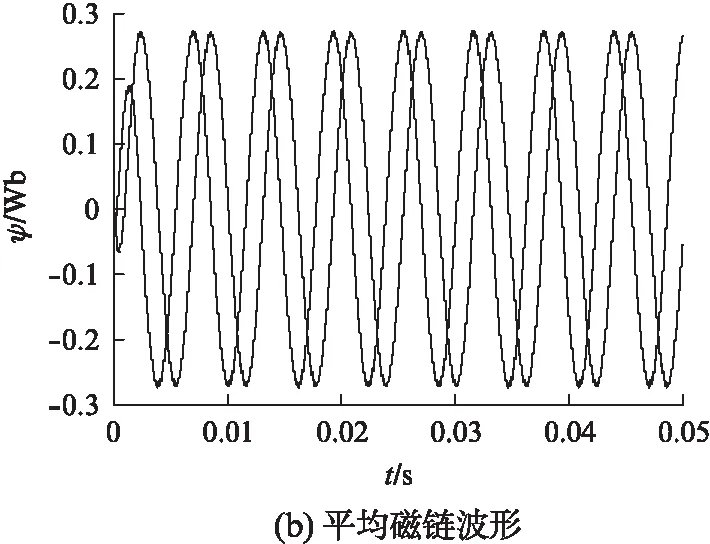
图8 并联电机的平均磁链轨迹与平均磁链波形

4 结 语

本文研究了空间矢量调制的直接转矩控制(DTC-SVM)策略，并将此策略应用于多电机并联驱动系统中，将多台电机的状态和参数进行平均化处理，建立了多电机并联驱动的“平均电机”数学模型。仿真结果表明，采用DTC-SVM策略时，电机速度响应快、转矩波动小、波形平滑、电流谐波含量低、逆变器开关频率恒定。在转矩误差允许的范围内，多台电机的起动时间和转速基本一致，其转速误差小，达到了高速、协调运行控制要求。

【参考文献】

[1] 罗亚琴,孙建忠,刘然.基于转矩跟随主从控制策略的多电机同步控制[J].电机技术,2011(6)： 8-11.

[2] 高水华,彭佩怡,梅映新.多电机并联运行的应用研究[J].船电技术,2007,27(6)： 370-373.

[3] OZKOP E, OKUMUS H I. Direct torque control of induction motor using space vector modulation(SVM-DTC)[C]∥2008 12th International Middle East Power System Conference, 2008： 368-372.

[4] 张华强,王新生,魏鹏飞,等.基于空间矢量调制的直接转矩控制研究[J].电机与控制学报,2012,16(6)： 13-18.

[5] VASUDEVAN M, ARUMUGAM R. New direct torque control scheme of induction motor for electric vehicles[C]∥5th Asian Control Conference, 2004(2)： 1377-1383.

[6] 万衡,吴韬,徐婧玥,等.基于直接转矩控制的单逆变器多机驱动系统[J].电机与控制应用,2011,38(10)： 36- 46.

[7] LEVI E. Multiphase electric machines for variable-speed applications[C]∥IEEE Transactions on Industrial Electronics, 2008,55(5)： 1893-1909.

[8] MOHAPATRA K K, KANCHAN R S, BAIJU M R, et al. Independent field-oriented control of two split-phase induction motors from a single six-phase inverter[C]∥IEEE Transactions on Industrial Electronics, 2005,52(5)： 1372-1382.