基于三角模糊数的风电场建设风险评价模型

程亮

(中国水利电力物资上海公司，上海市 200063)

基于三角模糊数的风电场建设风险评价模型

程亮

(中国水利电力物资上海公司，上海市 200063)

针对风电场建设单位在风电场建设风险评价中偏好使用传统工具且评价效果受主观偏好、信息不全面影响的现状，结合层次分析法(analytic hierarchy process，AHP)、模糊综合评判(fuzzy synthetic evaluation，FSE)构建了基于三角模糊数的模糊层次风险评价模型。为提高风险评价的准确性，利用FSE扩大信息量、使用两两比较判断矩阵计算风险因素排序权重，并采用三角模糊数刻画人类思维的模糊性。实例应用的结果证明,该模型层次分明、操作简单的特点使其在风电场建设的风险评价实践中具有可行性。

风电场；层次分析法(AHP)；三角模糊数；风险评价

0 引 言

从2011年开始，我国风电发展进入转型期，之前几年快速发展带来的速度与效益的矛盾逐渐显现。随着清洁发展机制(clean development mechanism，CDM)收益的降低、建设地点向内陆和海上等施工难度较高的地区扩张、电网限电越来越频繁等情况的出现，风电场的盈利水平也将日趋微薄，控制风险将成风电场建设成败的关键。目前，我国风电场建设一般只通过可研报告中对项目的敏感性分析进行项目风险评价，不能全面客观地反映建设风险发生概率和风险损失对项目的影响。此外，由于风电专业人才稀缺，在项目建设过程中人为因素对风险水平的影响有时甚至超过了外界环境因素对风险水平影响。

我国的风险管理虽然起步较欧美国家晚，但在涉及国计民生的大型水利电力工程领域的风险管理实践仍然取得了一定的成果，Monte-Carlo模拟[1]、IRM解释结构模型[2]、风险元传递及BP神经网络[3]等先进的风险管理方法都取得了较好的效果。风电场作为新型可再生发电项目，相对于大型水利电力项目而言，周期较短、前期投资较低，建设单位对风险管理不够重视，缺乏行业统一建立的风险资料库，很难通过概率统计对风电场风险进行分析评价[4]。因此，风电场建设风险的相关文献中偏好采用如LEC分析法[5]、风险评估矩阵[6]、德尔菲法等依托于专家经验的工具，无法反映风电场建设风险因素的复杂性、不确定性，而专家的主观偏好和信息不全面等问题也会影响结果的可靠性。在其他工程建设领域的风险评价实践中，为克服这些问题做出了积极的研究，如文献[7-9]把层次分析法(analytic hierarchy process，AHP)扩展为F-AHP并和模糊综合评判(fuzzy synthetic evaluation，FSE)结合使用，对风险因素按层次分解，利用两两比较模糊互补矩阵量化风险因素，降低评价过程中受到的主观影响，提高风险评价的系统性、可靠性；文献[10]以三角模糊数刻画风险因素的不确定性及人类思维的模糊性，计算风险因素的排序权重。本文利用上述的研究成果，将其引入风电场建设风险评价实践中，提出基于三角模糊数的模糊层次分析评价模型，供建设单位参考。

1 风险评价的理论基础

1.1 风电场建设风险的定义

风电场建设工程是一项周期长、投资大、控制环节多的综合性社会活动，本文将其中存在的逆向选择风险、道德风险及能力风险[11]统称为风电场建设风险。风险包含发生的不确定性及其引起的后果，每个事件的风险应该定义为不确定性和后果的函数[12]

R=f(P,L)

(1)

式中：R为风险；P为发生概率(不确定性)；L为风险损失(产生的后果)。

1.2 层次模型的评分标准

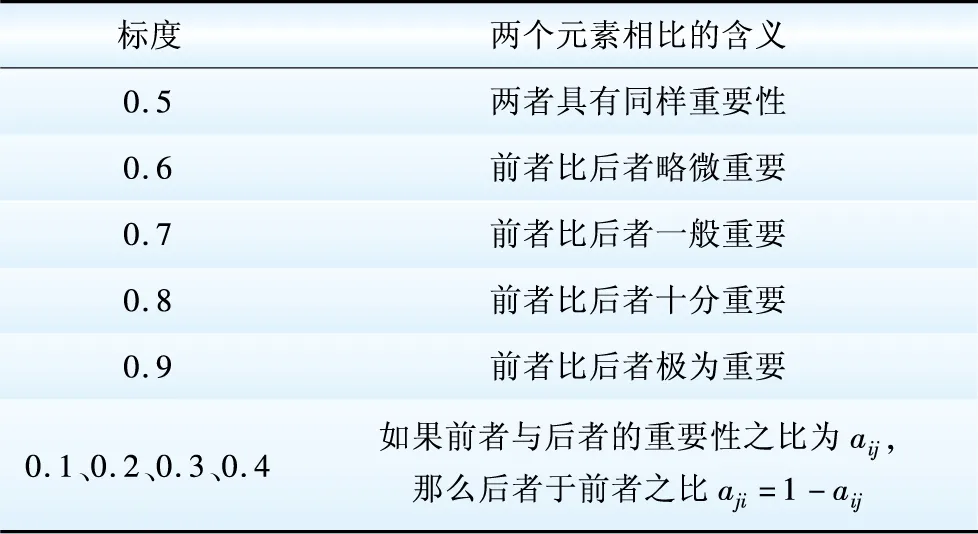
因为考虑到人的思维存在主观偏好以及语言的模糊性，克服传统AHP中比例标尺1到9离散刻度的不足之处，本模型采用表1所示比例标度[13]为三角模糊数(lij, mij, sij)赋值，其中lij, mij, sij分别表示最悲观值、最可能的值、最乐观的值。

表10.1到0.9比例标度

Tab.1Proportionalscalingfrom0.1to0.9

1.3 三角模糊数互补判断矩阵

定义1对于任意实数i和j，假设判断矩阵A=(aij)n×n，其中aij=(lij, mij, sij)，aji=(lji, mji, sji)为三角模糊数，且lij≤mij≤sij。若矩阵A满足以下条件[14]：(1)lii=mii=sii=0.5；(2)当i≠j，lij+ sji=mij+ mji= sij+ lji。称A是基于三角模糊数的互补判断矩阵。矩阵中的元素aij表示xi与xj的相对关系。

1.4 三角模糊数的期望值

考虑到语言的不确定性和人类思维的模糊性，本模型使用期望值E统计三角模糊数，即将元素i和元素j重要性比较判断的结果用三角模糊数的下界l、中值 m、上界s及其模糊概率p来描述。

以中值m为界，分等概率情况考虑[15]。根据l与m的偏离程度，确定结果是m的可能性是l的N倍；同理，根据m与s的偏离程度，确定结果是m的可能性是s的M倍，则l,m,s的模糊概率分别为

(2)

在本文中，经过与专家的探讨，在风电场中认为M=N=1。则三角模糊数的期望值为

E=pll+pmm+pss=l/4+m/2+s/4

(3)

1.5 模糊互补判断矩阵的一致性检验

在实际决策中采用加性一致性矩阵会较为简单、直观，也便于调整[16]。

定义2设模糊互补判断矩阵A=(aij)n×n和B=(bij)n×n，考虑到矩阵A和B中有n个aii-bii=0，定义A和B的相容性指标为

(4)

定义3设ω=[w1,w2,…,wn]T为模糊互补判断矩阵A=(aij)n×n的排序向量，定义矩阵C=(cij)n×n =(α(wi-wj)+0.5)n×n为A的特征矩阵，其中

(5)

考虑到存在n个aii-wii=0，则A和C的相容性指标为

(6)

为了方便计算、简化工作量，在本文中取α=(n-1)/2。

由此可见，模糊互补矩阵A的不一致程度越高，则I(A,C)>0的程度越大。在实际决策中，因为人思维的局限性，完全一致的矩阵几乎不可能得到，我们对一致性设定一个期望值ε，作为接受矩阵A为一致性的指标。当I(A,C)<ε认可矩阵是具有一致性。风电场的风险分析是多因素复杂项目，通过计算机模拟，取ε=0.1[17]。本文采用三角模糊数的期望值Eij作为元素aij。

2 风电场建设风险评价模型的构建

2.1 建设风险评价指标层次模型

根据风险的特性，将风电场的建设风险粗分为外部和内部风险二大类，每一类由2级风险构成，其中外部风险参考文献[18]中的分类包含了政策经济风险、社会与环境风险、技术与管理(甲方不可控、乙方或第三方占优势的)风险3个方面的一级风险；项目内部风险由项目单位内部管理形成的(甲方可控或甲方占优势)风险。经过专家研讨并结合风电场建设方面的历史资料文献，将这些4类一级风险进一步细分为若干二级风险因素。

最终，形成如图1的风险层次模型。其中，总目标层为风电场建设风险，控制层为风险的发生概率P及风险损失L；一级指标层分为一级风险指元素集Ui构成，与控制层具有交错关系；二级指标层为分解后的风险因素(*仅适用于与海上风电项目)。

图1 风电场建设风险评价指标模型

2.2 风电场建设风险评价步骤

根据本文对风险的定义1，以发生概率P和风险损失L这2个特征为目标对所有的风险元素进行评判，本文假设特征P及L为平行关系(权重都为0.5)。假设有m个二级指标元素，将数据进行归一化处理后，按照假设的权重得到建设风险的单因素模糊判断矩阵R=(rij)m×5。

2.2.1 确定F-AHP的权重向量

(7)

式中，用简单平均的方式统计了专家的偏好

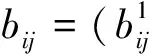
(8)

按照同样的方法进行一致性检验，并得到该元素集子准则层的权重向量Wii=[wi1,wi2,…,wij]T。

(2)构造一级判断矩阵及其一致性检验。由k位专家分别以P及L为准则对元素集Ui进行重要度的两两比较，按照上一步骤相同的方法和规则分别构建一级指标层比较判断矩阵ALq和APq，并根据式(6)逐一建立特征矩阵CLq和CPq且进行一致性检验，最终分别由式(8)得到一级指标层模糊综合评价矩阵AP及AL。对AP及AL也应逐一通过建立特征矩阵CL和CP进行一致性检验。本文假设特征P和L属于平行关系，因此将AP及AL得到的权重向量WP及WL按照权重0.5合成为一级指标层的排序向量WLP=[w1LP,w2LP,…,wnLP]T。

(3)确定总排序权重向量。假设共有m个二级指标因素，将二级指标层和一级指标层当元素排序权重向量合成得到F-AHP的总排序向量为

(9)

(4)合成评价结果。将总排序权重向量ω与单因素模糊判断矩阵R采用M(+,·)模糊算子[19]进行合成，得到模糊评价集B′。选择一种评价指标处理方法对项目的风险等级给出最终的评价。

3 应用实例

3.1 风电场概况

某风电场拟装机容量45 MW，拟安装15台1 000 kW和20台1 500 kW风电机组。场区属于豫西丘陵区，北临黄河，南部有秦岭支脉，地形呈现东南高西北低。场区属于暖温带大陆性季风气候，冬春季易发生大风，属于较明显的内陆山地风场。本次风险评价共由5位专家对各因素进行比较，并通过算术平均数统计专家的偏好。

3.2 风险评价结果

3.2.1 建立风险元素集

一级风险指标元素集：P=L={U1,U2,U3,U4}={政策经济风险，社会与环境风险，技术与管理风险，项目内部风险}。

二级风险指标元素集：U1={u11,u12,u13,u14}={政府支持，电价批复，法律法规，融资汇率}；U2={u21,u22,u23,u24,*u25}={当地民生，气候因素，自然灾害，地质条件}；U3={u31,u32,u33,u34}={电网限电，施工组织，运行维护，风能资源}；U4={u41,u42,u43,u44}={CDM开发障碍，风机选型，合同管理，项目团队}。

3.2.2 建立风险评语集

V={v1,v2,v3,v4,v5}={高风险，较高风险，中等风险，较低风险，低风险}。

3.2.3 建立单因素模糊评判矩阵

将5位专家的统计结果经过归一化处理后，假设条件P及L之间不存在优先关系，将上述条件P及L的模糊关系合成，得到本模型的单因素模糊评判矩阵

3.2.4 确定F-AHP的权重向量

(1)二级指标权重计算。

表2～5是以一级风险因素为准则进行两两比较判断并进行一致性检验的过程，并分别得到各准则的二级指标权重Wii。

表2 以U1为准则的两两比较判断矩阵

注：相容性指标I11=0.047<0.1

表3 以U2为准则的两两比较判断矩阵

注：相容性指标I22=0.02<0.1

表4 以U3为准则的两两比较判断矩阵

注：相容性指标I33=0.043<0.1

表5 以U4为准则的两两比较判断矩阵

注：相容性指标I44=0.009<0.1

(2)一级指标权重计算。

表6、7是以P及L为准则进行两两比较判断并进行一致性检验的过程，分别得到一级指标权重WP和WL。

表6 以P为准则的两两比较判断矩阵

注：相容性指标IP=0.014<0.1

表7 以L为准则的两两比较判断矩阵

注：相容性指标IL=0.018<0.1

假设条件P及L为平行关系，将2个向量取算数平均值合成得到一级指标层的权重向量：WLP=[0.238,0.258,0.275,0.229]。

(3)层次模型总排序权重ω计算。

将上述2步骤得到的权重向量合成推求总排序权重ω，计算过程见表8。

3.2.5 合成评价结果

B′=ω·R=[0.166, 0.312, 0.352, 0.085, 0.084]将层次模型的总排序权重向量ω与单因素模糊判断矩阵R按照M(+,·)模糊算子进行合成对模糊评价集B′按照最大隶属度原则进行处理：最大值为0.352，对应评语集V的v3中等风险。

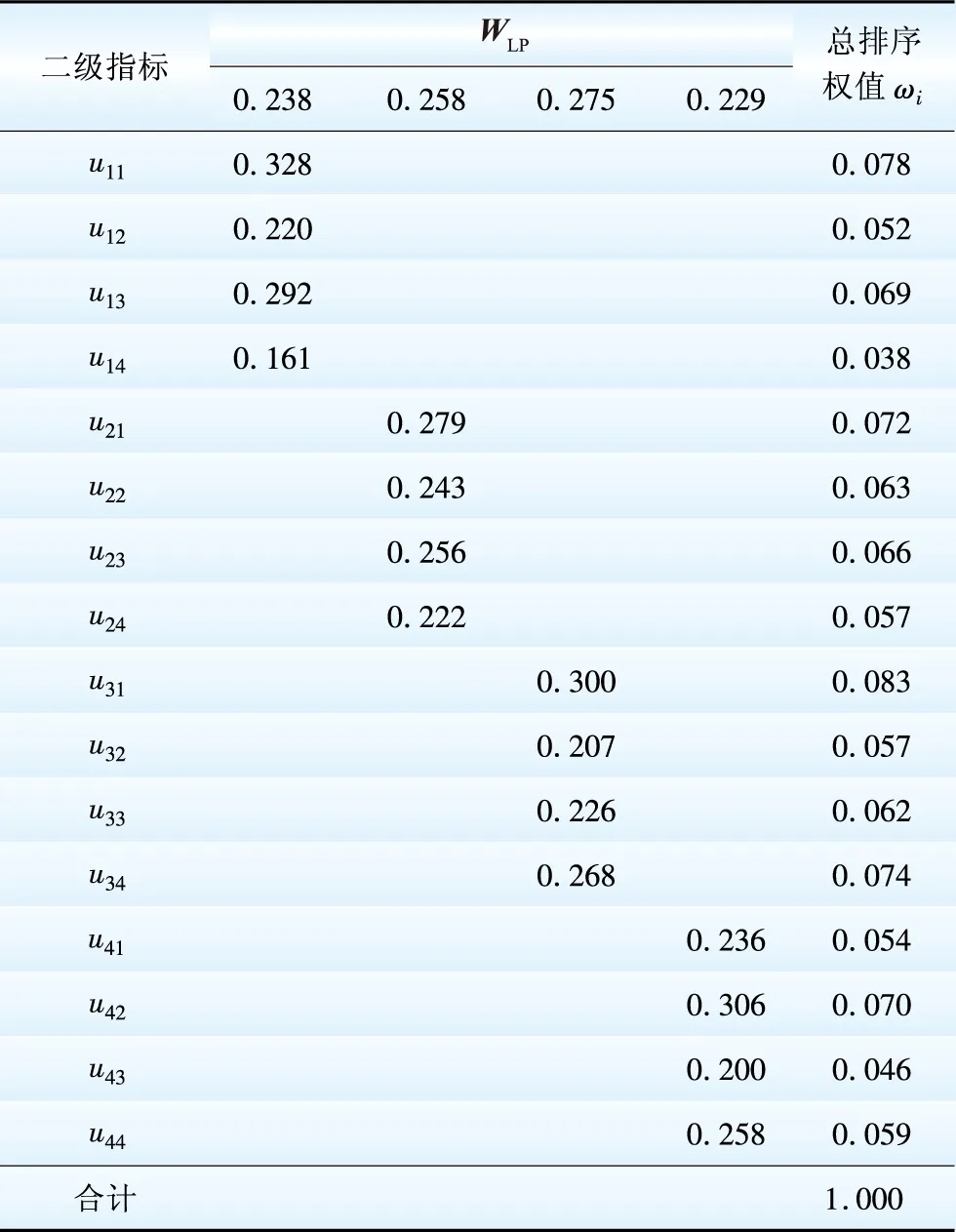
表8 总排序权重计算

4 结 论

(1)将模糊集引入AHP判断矩阵构造过程中，使得AHP扩展为F-AHP，克服经典AHP不能完全反映人类思维的问题，利用三角模糊数刻画了复杂巨系统决策问题中人主观思维判断过程的模糊性，扩大信息量，使数学模型的量化过程能更精确地趋于实际。

(2)FSE与F-AHP的结合，将识别出的风险元素构建为更加直观的递阶层次结构，便于决策者全面掌握风险信息；将综合评判中简单权重赋值升级为通过具有层次结构的两两比较判断矩阵计算出权重，经过一致性检验的比较结果更加客观准确，降低了主观偏好和信息不全面带来的弊端。

[1]骆珣，贾建容.基于蒙特卡洛模拟的火电建设项目投资风险估计[J].北京工商大学学报：自然科学版，2006，24 (3):66-68.

[2]程鸿群，汪程程.火电建设项目投资风险结构模型[J].武汉大学学报：工学版，2012，45(S):318-321.

[3]王素花.1000 MW级火电项目前期风险元传递模型[J].电力建设，2014，34 (11):125-128.

[4]孔昭东，周宏胜，刘锦国，等.大型风电工程建设项目风险管理模式探讨[J].内蒙古电力技术，2008，26 (4):30-32.

[5]邹炅，章显亮，黄善平，等.基于风险评估矩阵的风电项目风险管理研究[J].中国电力，2012，45 (9):56-75.

[6]吴启仁，郑主平，孙向东.风电场建设风险管理[J].水利水电技术，2009，40 (9):18-21.

[7]李雅妹，张晓梅，张蒙.基于模糊综合评价模型的项目风险评估 [J].今日湖北，2011(2):22.

[8]姬东朝，宋笔锋，喻天翔.基于模糊层次分析法的决策方法及其应用[J].火力与指挥控制，2007，32 (11):38-41.

[9]朱明明.基于模糊层次分析法的工程项目风险评估[J].科技管理研究，2010(20):214-217.

[10]韩喜双，刘仁辉，张劲强.三角模糊数的工程项目风险识别[J].哈尔滨工业大学学报，2008，40 (10):1617- 1620.

[11]时现，毛晔，许长青，等.工程项目控制：理论·实务·案例[M].大连：大连出版社，2013:30-31.

[12]王颖.项目风险管理[M].北京：电子工业出版社，2012:1-23.

[13]张吉军.模糊层次分析法(AHP) [J].模糊系统与数学， 2000，14(2):80-88.

[14]杨静，邱菀华.模糊互补判断矩阵一致性检验和改进方法 [J].系统管理学报，2010，19(1):14-18.

[15]李华，肖钰.基于三角模糊数的判断矩阵的改进及其应用[J].模糊系统与数学，2003，17(2):60-64.

[16]姜艳萍，樊治平.互补判断矩阵一致性改进方法[J].东北大学学报，2003，24(11) :98-101.

[17]公彦德，曾雪兰，吉建华.模糊互补判断矩阵的一致性检验及调整方法[C]//2005中国控制与决策学术年会论文集(下).沈阳：东北大学出版社，2005:1966-1968.

[18]李俊峰.2012年中国风电发展报告[R].北京：中国环境科学出版社，2012:23-38.

[19]孙亚胜. 模糊网络分析在海上风电项目风险评价中的应用[D].大连：大连理工大学，2008.

(编辑：蒋毅恒)

ConstructionRiskEvacuationModelofWindFarmBasedonTriangularFuzzyNumber

CHENG Liang

(China National Water Resource & Electric Power Materials & Equipment Shanghai Co., Ltd., Shanghai 200063, China)

Aiming at the current condition, which most of wind farm investors prefer using traditional tools for risk evaluation, and the evaluation results are usually affected by subjective preferences and incomplete information, this paper integrated AHP (analytic hierarchy process) and FSE (fuzzy synthetic evaluation) to establish the F-AHP model of risk evaluation based on triangular fuzzy number. To improve the accuracy of risk evaluation, this paper used FSE to enlarge the volume of information, utilized pairwise comparison judgment matrix to calculate the rank weights of risk indexes, and also used triangular fuzzy number to describe the fuzzy nature of human thinking. Application result shows that the model is feasible in the practice of construction risk evaluation for wind farm because of its clear structure and simple opration.

wind farm; analytic hierarchy process(AHP); triangular fuzzy number; risk evaluation

TM 614

： A

： 1000-7229(2014)09-0103-06

10.3969/j.issn.1000-7229.2014.09.019

2014-03-07

：2014-04-03

程亮(1981)，男，管理学硕士，工程师，工程建设项目管理，E-mail：ballackcl@126.com。