两种算法的理论分析

李 梅

(西南大学 数学与统计学院，重庆 400715)

如今，密码体制的安全性已被人们所重视，在生活中变得尤为重要，而一些密码体制可能会因为密文而泄露明文的部分信息，Oracle RSA Decryption(n，b，y) 算法却证实了RSA密码体制在一类此种类型的攻击下是安全的.同样的，Elgamal密码体制的安全性也是基于离散对数logαβ的难解性，L2Oracle-Discrete-Logarithm(p，α，β)算法也证明了在已知β的情况下，离散对数的比特安全性.

1 算法Oracle RSA Decryption(n，b，y)

设n=pq，p，q为素数，P=C=Zn，定义K={(n，p，q，a，b)：ab≡1(modφ(n))}.对K=(n，p，q，a，b)，定义ek(x)=xbmodn，dk(y)=yamodn，(x，y∈Zn)，其中n，b为公钥，p，q，a为私钥.

external Half

k←[log2n]

fori←0 tok

l0←0

hi←n

fori←0 tok

return ([hi])

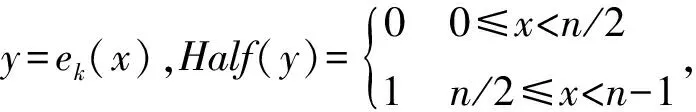
2 算法L2 Oracle-Discrete-Logarithm(p，α，β)

2.1 离散对数

(G，·)为一乘法群，α∈G，其阶为n，β∈<α>，若αx=β，0≤x≤n-1，则记x=logαβ，称其为β的离散对数.

2.2 算法L2 Oracle-Discrete-Logarithm(p，α，β)

externalL1，OracleL2

x0←L1(β)

β←β/αx0modp

i←1

Whileβ≠1

return(xi-1，xi-2，…，x0)

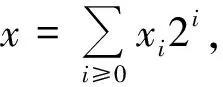
3 算法分析

1) Oracle RSA Decryption(n，b，y)算法中，因为y=ek(x)=xbmodn，所以ek(x1)ek(x2)=ek(x1x2).因此在算法的第一个for循环中，hi=half(y×(ek(2))i)=half(ek(x·2i))，又

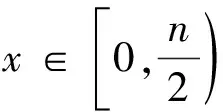
(1)

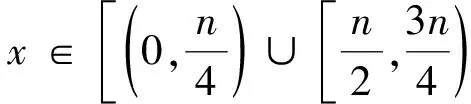
(2)

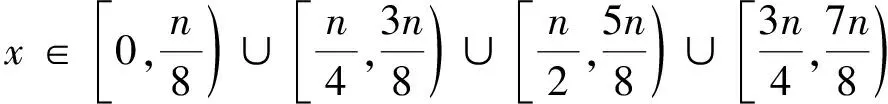
(3)

…

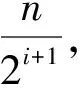
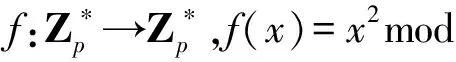
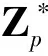
(4)

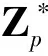
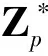
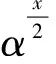
4 总 结

对这两种算法作出了分析，使得算法的成立性显得更加自然合理，两种算法均证明了明文的安全性，Oracle RSA Decryption(n，b，y)算法从明文x的所属区间出发从而得到x，而L2Oracle-Discrete-Logarithm(p，α，β)算法则是从明文信息比特的角度出发得到x，从以上算法的分析中，也可以看出信息比特安全的重要性，在今后密码学的发展过程中，更加值得重视.

参考文献：

[1] DOUGLAS R S.密码学原理与实践[M].北京：电子工业出版社，2009

[2] GOLDWASSER S，MICALI S，TONG P. Why and How to Establish a Private Code on a Public Network[A]. Proceedings of the 23rd Annual Symposium on Foundations of Computer Science (FOCS’82)[C].Chicago，Illinois，1982：134-144

[3] 陈笑伟.关于离散对数比特问题的一个新发现[J].科技创新导报，2009(3)：231-233

[4] 斯·廷森D R.密码学原理与实践[M].2版.冯登国，译.北京：电子工业出版社，2009

[5] 刘玉君.信道编码[M].郑州：河南科学技术出版社，1992

[6] PERALTA R. Simultaneous Security of Bits in the Discrete Log[A]. Proceedings Eurocrypt’85[C].Springer LNCS，1986(219)：62-72

[7] 离散对数的比特安全性[J].浙江大学学报：工学版，2013，30(8)：23-27

[8] LONG D L，WIGDERSON A.The discrete log hides O(log n) bits[J]. SIAMJ Computing，1988(17)：363-372