自由活塞内燃发电机稳态压缩比控制

许大涛,左正兴,冯慧华,田春来

(北京理工大学机械与车辆学院, 100081, 北京)

自由活塞内燃发电机稳态压缩比控制

许大涛,左正兴,冯慧华,田春来

(北京理工大学机械与车辆学院, 100081, 北京)

为解决自由活塞内燃发电机的稳定控制问题,根据能量守恒定律建立了连续运行过程周期能量转化与传递模型。通过数值仿真分析,获得了满足稳定运行的基本能量平衡条件,包括压缩能和系统能量余值方程,从而实现了周期能量余值和压缩能的稳定变化。以压缩比为目标建立了连续周期能量动态平衡的控制系统及策略,即以喷油量和压缩比为控制输出变量,采用比例-积分-微分控制器进行控制,进而实现了可控压缩比的连续稳定运转。研究结果表明:采用所建控制系统及策略后,自由活塞内燃发电机运行可靠、稳定;压缩比在负载变化后出现短暂振荡,但经多个周期后恢复稳定,缸内峰值压力和运行频率具有相似的变化趋势,各参数变化均在可接受的范围内。

自由活塞内燃发电机;控制策略;压缩比;数值仿真

自由活塞内燃发电机是一种新型动力装置,它将自由活塞内燃机的活塞与直线发电机次级连接在一起,利用燃烧室内燃烧产生的气体爆发压力推动活塞运动,直线发电机产生感应电能并向外部输出。该发电机结构简单、紧凑,能量传递路径短,在功率密度、转换效率和排放等方面具有众多潜在的性能优势[1]。这些性能优势及其在动力电源领域的良好应用前景,引起了研究人员的广泛关注。Atkinson等人以性能数值仿真为基础,针对二冲程点燃式双活塞对置型自由活塞内燃发电机开展了试验研究[2]。Mikalsen等人针对单自由活塞的二冲程自由活塞内燃发电机开展了研究,并设计了一种止点预测控制方法,其从上一周期的运行特性和性能特性中计算得到了目标上止点位置[3]。Xu等人针对单自由活塞的四冲程自由活塞内燃发电机建立了分层次的控制系统,对能量流动进行了有效控制[4]。Xiao等人针对双活塞对置型自由活塞内燃发电机的活塞运动特性及性能参数化影响规律进行了仿真优化研究,通过各参数匹配组合获得了期望的频率[5-6]。Mao等人针对双活塞对置型自由活塞内燃发电机建立了运行过程非线性系统动力学模型,利用数值建模和混合系统求解的方法,获得了活塞的运动规律,同时分析了运动特性对性能的影响,获得了一阶近似的理论解,归纳了系统稳定运行的匹配条件[7-8]。

由于没有曲轴连杆的机械限制,特殊的活塞运动使得自由活塞内燃发电机的稳态控制策略成为当前研究的主要问题之一。建立有效的控制系统及策略是实现样机稳定运行和系统产品化的首要保证。目前,仅有少数研究者借鉴液压自由活塞内燃机的研究成果提出了初步设想,但有关双活塞对置型自由活塞内燃发电机的控制问题尚未完全解决[9]。文献[10]利用简化的系统能量守恒模型对控制系统进行了研究,通过精确的液压控制系统对周期燃烧放热波动及其引起的能量平衡状态失稳进行了干预,以抵消能量偏差余值。本文根据文献[10]的液压自由活塞内燃机控制方法,提出了一种以压缩能量稳定为目标的控制策略。根据自由活塞发动机结构特点和控制系统目标要求,通过能量传递过程分析获得了稳定运行的能量平衡状态,利用性能仿真模型模拟了全周期运行过程,并验证了控制策略的有效性。

1 自由活塞内燃发电机原理及控制

本文研究对象是一种二冲程双活塞对置型自由活塞内燃发电机,结构如图1所示。该发电机由水平对置的2个自由活塞内燃机构成,其中间布置有直线电机,2个活塞与发电机次级固定在一起,内燃机采用二冲程压缩燃烧循环方式,燃料通过喷油器在适当的时刻直接喷入气缸。运行过程中内燃机的进排气采用扫气口方式,即通过活塞运动开启进气口和排气口,实现缸内扫气。

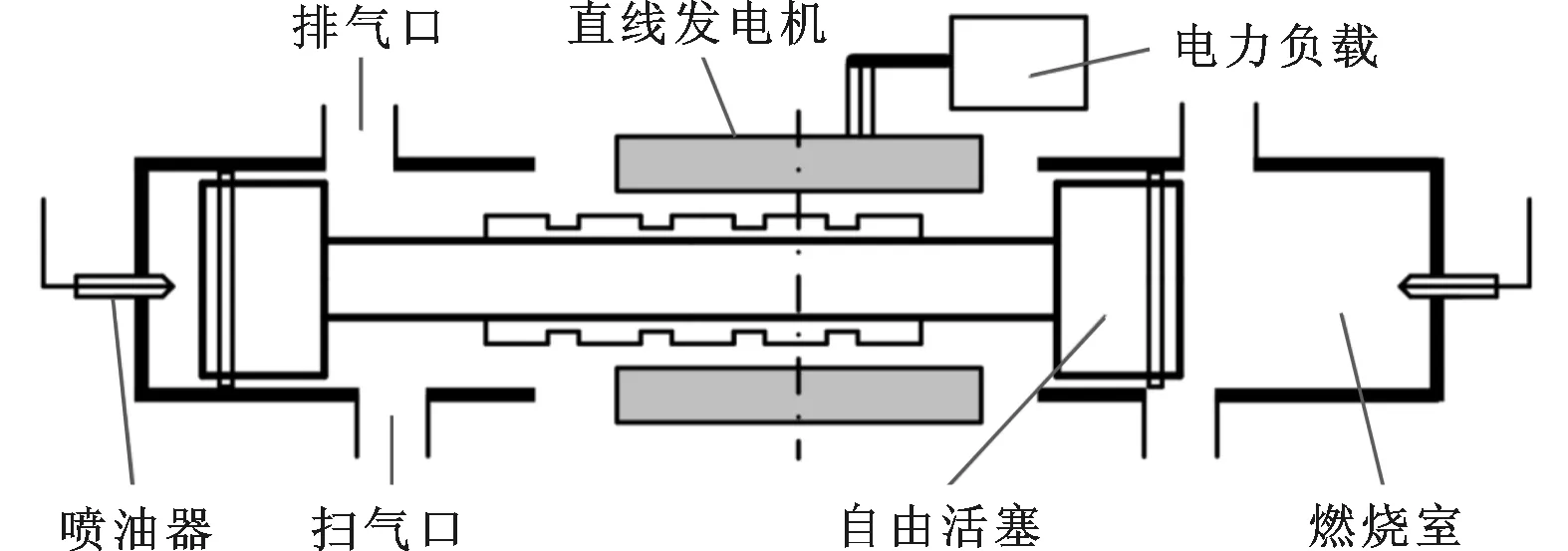
图1 自由活塞内燃发电机结构

启动时,电机作为电动机推动活塞往复运动,促使燃烧室达到压缩燃烧条件;点火后,电机即刻转换为发电机。运行过程中左侧燃烧室燃烧后,瞬间增大的气体爆发压力推动活塞向右运动,待活塞运动到达右侧上止点附近时,缸内喷油并点火燃烧后再将活塞推回,继而实现左右气缸交替点火的连续运行。由于与传统内燃机结构不同,自由活塞内燃发电机的止点是指自由活塞在往复运动过程中,活塞速度为0的位置,此时活塞位移与活塞行程之比的倒数即为自由活塞内燃发电机的压缩比。

活塞在两侧止点之间进行往复运动,理想情况下连续周期运行过程如图2所示,图中示意了理想的喷油信号和压缩比曲线。因为不需要额外的回弹装置,能量可以最大限度地保留在系统之内,所以与单活塞和四冲程循环的自由活塞内燃发电机相比,本文发电机在同一周期内没有非做功行程,单位周期做功次数多,表明具有较高的功率密度。

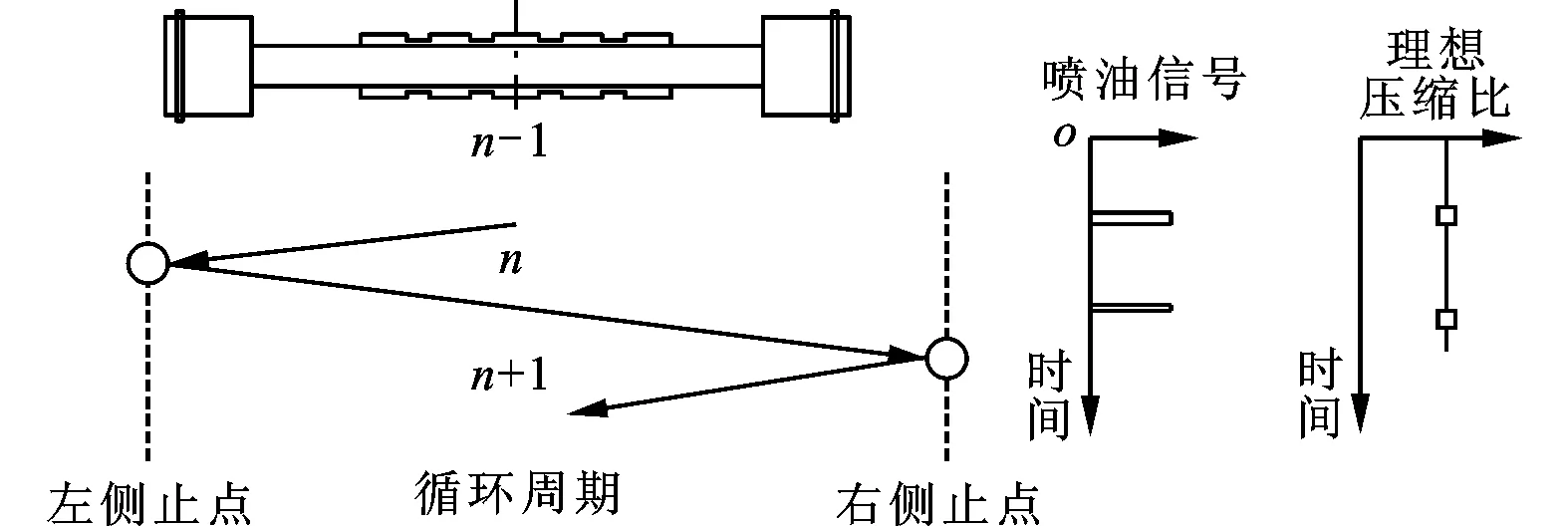
图2 理想情况下活塞连续周期运行过程

自由活塞内燃发电机的控制问题是由其结构特点和运行方式引起的。在实际运行过程中,燃烧或负载时常发生波动,引起活塞运动不稳定,系统由此产生失稳倾向。如果未采取有效的稳定控制方法,燃烧波动或负载变化直接影响活塞运动,继而影响扫气和燃烧过程,造成的结果是活塞无法达到预定止点,使得缸内出现熄火,或是行程过长导致撞缸。虽然曲轴连杆的摒除带来了众多性能优势,但也带来了多变量控制的复杂性,提高了维持运行的难度。控制系统及策略是稳定运行的关键,也是当前研究急需解决的问题之一。

2 能量转化与传递过程

从能量平衡角度来看,自由活塞内燃发电机的稳定运行过程就是系统能量稳定转化与传递的过程。尽管不再受到机械机构的束缚,但是自由活塞的往复运动仍然受燃烧室内气体作用力、摩擦力和电机电磁阻力的作用,这3个力的合力决定着活塞的运动规律,同时活塞运动又直接影响缸内进排气、压缩和燃烧过程,以及电机电磁转化过程等。能量转换直接通过活塞运动实现,燃烧释放的燃料化学能作为缸内气体内能,一部分通过活塞动能转化为发电机的电能,另一部分作为扫气、散热和摩擦等的损失能量。因此,分析能量转化与传递过程,通过控制策略获得稳定的能量流动过程,是一种有效的控制方法。

根据自由活塞内燃发电机的基本运行原理,将周期定义为活塞从一侧止点运动到另一侧止点的时间。在一个周期内,系统能量平衡方程为

Ei-Ef-Ee-Es=0

(1)

式中:Ei为燃烧释放总能量;Ef为摩擦损失能量;Ee为电机感生电能;Es为传热、扫气损失能及其他散热损失。

从式(1)中可以发现,虽然能量转化是通过活塞动能来实现的,但是动能并没有直接体现出来,这是因为活塞动能作为中间过程量只体现在特定时刻上。

从图2的连续周期运行过程可以发现,两侧燃烧室相差半个循环周期。当活塞接近右侧止点和压缩燃烧室内的气体时,当前周期中的部分能量作为压缩能传递到下一个周期,从而影响下一周期的燃烧过程。

如果将摩擦和扫气损失等损耗能量一并计入电机感生电能,那么第n和n+1两个连续周期的能量传递可以表示为

Ei(n)+Ep(n)-Ep(n+1)-Ee(n)=0

(2)

式中:Ep为燃烧室内气体在压缩过程中获得的压缩能。压缩能的变化为

ΔEp(n+1)=Ei(n)-Ee(n)

(3)

根据式(3),压缩能变化来自于上一周期的能量余值。于是,合理匹配各能量关系,降低周期能量余值,可以降低压缩能波动。

根据热力学定律,燃烧室内气体通过活塞压缩获得内能,即压缩能

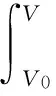
(4)

式中:p0和V0分别为压缩初始时刻燃烧室内气体压力和体积;γ为热容比。通过积分可以获得

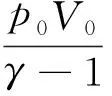
(5)

式中:R为压缩比。

通过式(5)、利用活塞位移计算得到压缩比,表征压缩能及其变化,就可以获得能量传递的差异。如果能够对该差异进行控制,以此建立连续周期能量动态平衡的控制策略,就可以获得有效的能量平衡匹配和活塞运动控制,降低燃烧波动,实现稳定运行目标。

3 压缩比稳态控制策略

自由活塞内燃发电机的稳定控制的首要目标是获得稳定的燃烧和压缩过程,避免缸内失火或活塞撞缸。具体到自由活塞内燃发电机的实际控制系统,作为唯一的系统输入能量,燃烧产生的气体爆发力是影响活塞运动的关键,因此首要的控制策略应以内燃机控制为主展开。活塞摩擦力是固有机械损耗,一般不可控制;电机电磁阻力是连续作用在活塞及动子上的,由电机结构参数决定,并直接影响输出功率等性能指标,可以用于后续的性能优化与匹配控制。

气体爆发压力由燃烧放热决定,压缩过程产生的压力和温度直接影响燃烧。在压缩过程中,缸内压力和温度逐渐升高,活塞动能转化为空气内能。为了获得稳定的燃烧放热和连续的能量传递平衡状态,必须控制压缩过程,即对压缩能和压缩比进行有效控制。在实际的自由活塞内燃发电机设计中,样机采用气口式扫气方式,气口位置和开度已经固定,扫气过程由活塞运动情况决定。在不考虑喷油时刻对燃烧影响的前提下,实际可控制的只有喷油量。根据前述分析,建立控制策略如下。

假设系统稳态情况下压缩能目标值为Ep0,由式(2)得到的第n个周期的能量传递为

Ei(n)=Ep0(n+1)-Ep(n)+Ee(n)+u(n)

(6)

式中:u(n)为周期离散比例-积分-微分控制器的输出量。u(n)的计算式如下

u(n)=P(n)+I(n)+D(n)

(7)

(8)

式中:P(n)、I(n)和D(n)分别为控制器的比例项、积分项和微分项;KP、KI和KD分别为比例系数、积分系数和微分系数;e(n)是压缩能偏差项,表达式为

e(n)=Kc[Ep0(n+1)-Ep(n)]

(9)

其中Kc为偏差项增益系数。

假设每周期燃料燃烧释放能量与喷油量成正比例关系,则有

Ei(n)=Kim

(10)

式中:Ki为喷油量比例系数;m为喷油量。

设定参数在小范围变化时,式(5)描述的压缩比与压缩能可近似为正比例关系。假设KR为近似比例系数,则有

Ep(n)=KRR

(11)

以喷油量和压缩比为控制输出变量,联合式(6)～式(11),通过数学推导可获得控制策略的状态空间表达式

x(n+1)=Ax(n)+Bu(n)

y(n)=Cx(n)+Du(n)

(12)

式中:A、B、C和D为状态空间系数矩阵。各矩阵分别为

4 控制系统性能及结果

在前期自由活塞内燃发电机工作过程仿真研究中建立了全周期运行的数学模型,获得了系统性能及参数影响规律[8]。以此为基础,通过引入压缩比稳态控制策略来分析控制系统性能。设计样机缸径为60 mm,设定运行工况的压缩比为16,行程为65 mm,功率为7.5 kW,频率为35 Hz。在1.0 s之前系统为85%负荷运行;在1.0 s时刻,目标负载发生波动,输出电流以阶跃形式升高至90%负荷。当负载发生波动时,系统能量传递出现波动,通过控制系统调整喷油量,可获得稳定的能量平衡及运行过程。

4.1 控制系统稳定性

根据式(12)建立的状态空间方程,将实际结构和控制系统参数代入系统矩阵A,其特征值及根符合稳定性判据。该控制系统在实际参数约定的范围内是稳定的。

4.2 压缩比与止点

根据设定工况,输出电流增加将导致电磁阻力增大,引起压缩能下降,表现为活塞无法到达原定上止点,压缩比降低。压缩比变化曲线如图3所示。从图3发现,随着负载阶跃升高,压缩比出现明显下降,最小值为15.1,随后正向跃升到接近16.3,经过短暂振荡后恢复到设定值,并保持稳定。根据燃烧条件,压缩比达到最小值时,缸内燃料仍然可以压缩点火。

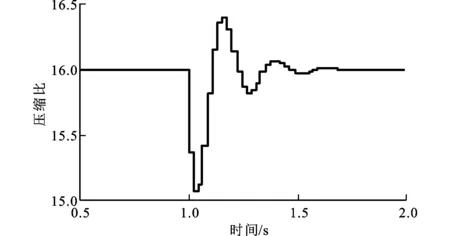
图3 压缩比变化曲线

止点偏差变化曲线如图4所示。从图4发现,在1.0 s时刻,活塞左侧止点位置出现约0.42 mm的偏差,随即进入振荡过程,并在1.5 s后恢复稳定。从图4还发现,两侧活塞的上止点偏差变化相似,过程近似相差半个周期。这种相似的变化过程也表现出双自由活塞对置型发电机的对称性和耦合性。考虑到活塞止点与燃烧室顶部存在间隙,止点偏差振荡峰值较小,不会出现撞缸。因为负载变化必然引起下一周期的压缩比和止点波动,所以为了保证连续的有效燃烧,避免缸内失火或撞缸,必须严格限制负载的波动范围。

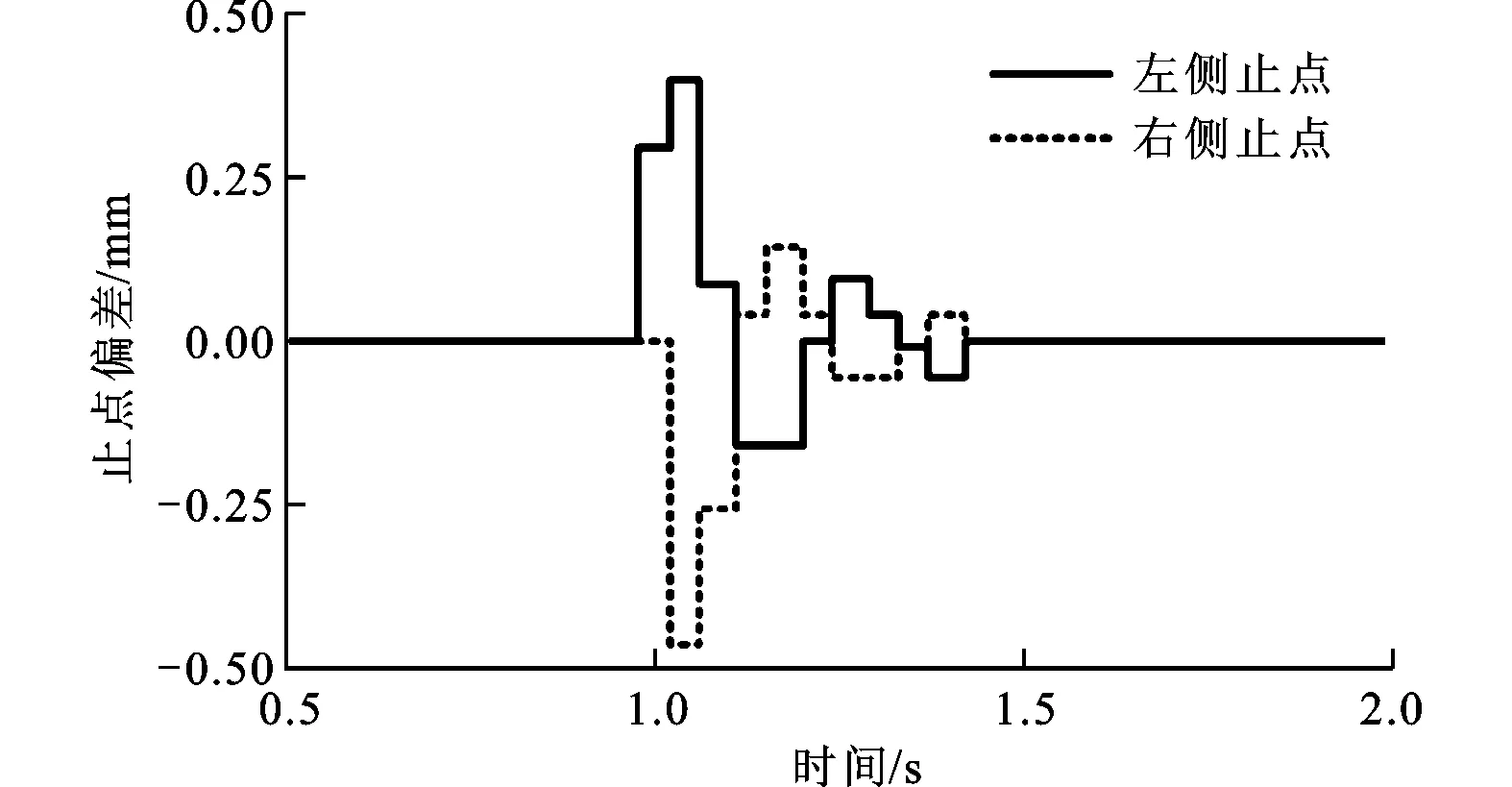
图4 止点偏差变化曲线

4.3 燃烧室内峰值压力

在控制系统作用下,压缩比变化出现振荡过程。随着压缩比的升高,燃烧室内峰值压力升高,过高的峰值压力会引起系统故障。缸内气体峰值压力变化如图5所示。比照图3可以发现,峰值压力变化趋势与压缩比类似,不同之处在于,压力终值稳定在7.17 MPa,比初值6.95 MPa略微升高。在压缩比峰值周期,峰值压力接近7.53 MPa,满足结构设计。两侧燃烧室内峰值压力变化趋势相同,与止点变化类似。

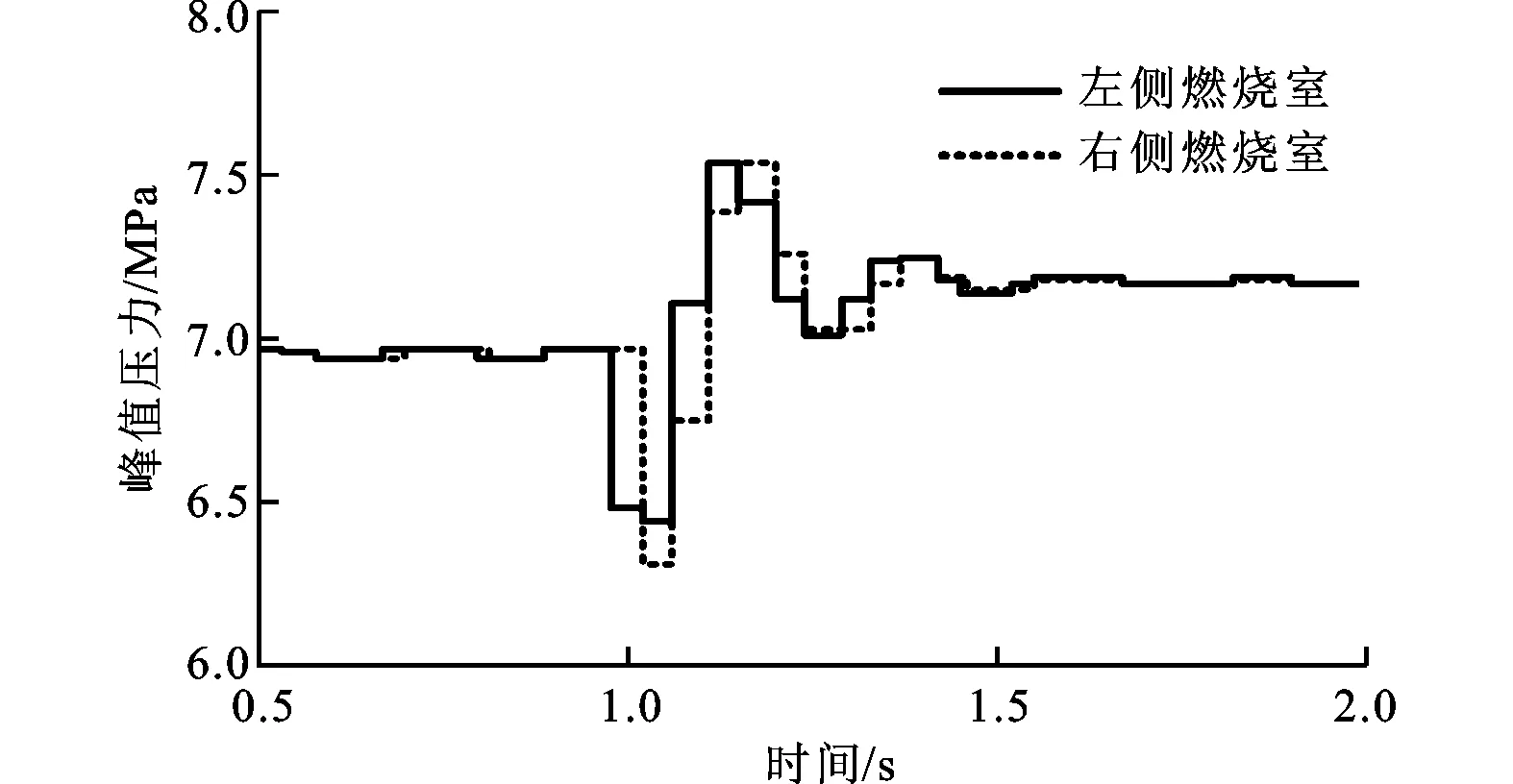
图5 缸内气体峰值压力变化曲线

4.4 活塞运动频率

活塞往复运动的频率变化如图6所示,其与峰值压力的振荡过程相似,终值较初值有所增加,并稳定在35.1 Hz。频率最小值为34.5 Hz,最大值为35.4 Hz,波动范围在-1.43%～1.14%之间,对电机感生电流品质影响不大。

图6 自由往复活塞运动频率变化曲线

通过各性能参数的变化规律可以看到,控制系统利用离散周期能量传递规律,实现了跟随负载波动变化的稳定运行控制。在负载变化后,系统通过多个周期的调整重新建立稳定状态。止点位置、缸内峰值压力和活塞运动频率均与压缩比变化趋势相近,体现出自由活塞内燃发电机多变量强耦合的特点。

5 结 论

(1)通过能量转化与传递过程的分析,设计了基于周期能量平衡的稳态控制系统。运行过程仿真结果显示,随着负载的增加,压缩比在下一个循环中明显降低,随后出现多个周期的振荡并逐渐恢复稳定。缸内峰值压力和活塞运动频率出现相似的变化,上升数值及其变化范围满足系统设计要求。

(2)本文设计的压缩比控制策略能够有效控制运行,保持稳定,提供了一种解决控制问题的方法,为试验研究提供了策略参考,也为可控的变压缩比运行提供了理论依据。

(3)对于负载变化后的多个周期的性能必须加以深入研究,压缩比振荡过程对自由活塞内燃发电机性能的直接影响和相关试验研究是后续工作的重点。

[1] MIKALSEN R, ROSKILLY A P. A review of free-piston engine history and applications [J]. Applied Thermal Engineering, 2007, 27(14/15): 2339-2352.

[2] ATKINSON C, PETREANU S, CLARK N, et al. Numerical simulation of a two stroke linear engine-alternator combination, SAE 1999-09-21 [R]. Washington DC, USA: SAE, 1999.

[3] MIKALSEN R, ROSKILLY A P. The control of a free-piston engine generator: part 1 Fundamental analyses [J]. Applied Energy, 2010, 87(4): 1273-1280.

[4] XU Z, CHANG S. Prototype testing and analysis of a novel internal combustion linear generator integrated power system [J]. Applied Energy, 2010, 87(4): 1342-1348.

[5] XIAO J, LI Q, HUANG Z. Motion characteristic of a free piston linear engine [J]. Applied Energy, 2010, 87(4): 1288-1294.

[6] 栾延龙, 李理光, 王哲, 等. 自由活塞发动机关键设计参数及其性能的仿真优化研究 [J]. 内燃机工程, 2010, 31(2): 15-21.

LUAN Yanlong, LI Liguang, WANG Zhe, et al. Key design parameters and performance optimization of a free-piston engine based on simulation [J]. Chinese Internal Combustion Engine Engineering, 2010, 31(2): 15-21.

[7] MAO J, ZUO Z, LI W. Multi-dimensional scavenging analysis of a free-piston linear alternator based on numerical simulation [J]. Applied Energy, 2011, 88(4): 1140-1152.

[8] 肖翀, 左正兴. 自由活塞发电机动力学过程的非线性模型 [J]. 北京理工大学学报, 2008, 28(11): 966-969.

XIAO Chong, ZUO Zhengxing. Nonlinear model and first order approximate solution of a free piston genera-tor [J]. Transactions of Beijing Institute of Technology, 2008, 28(11): 966-969.

[9] MIKALSEN R, ROSKILLY A P. Predictive piston motion control in a free-piston internal combustion engine [J]. Applied Energy, 2010, 87(5): 1722-1728.

[10]TIKKANEN S, VILENIUS M. Control of dual hydraulic free piston engine [J]. International Journal of Vehicle Autonomous Systems, 2006, 4(1): 3-23.

(编辑 苗凌)

StableCompressionRatioControlforFree-PistonEngineGenerator

XU Datao,ZUO Zhengxing,FENG Huihua,TIAN Chunlai

(School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China)

To stably control free-piston engine generator, a model of energy conversation and transfer in continuous cycles was established. The essential energy balance conditions satisfying stable operation were constructed via numerical simulation, including the equation of the compression energy and system energy residual value, then the stability of cyclic energy residual value and compression energy were sequentially achieved. The control system and strategy for dynamic energy balance in continuous cycle were proposed, where the injection quantity and the compression ratio were taken as the control output variables, the proportion-integral-derivative controller was employed to drive the operation, and the continuously stable operation under the controllable compression ratio thus was realized. The results show that the free-piston engine generator operates reliably and stably under the control system and strategy. The compression ratio shortly oscillates once changing load, then gets back to the set value after undergoing several cycles. The peak pressure in-cylinder and operation frequency tend similarly and the parameters vary within the acceptable range.

free-piston engine generator; control strategy; compression ratio; numerical simulation

10.7652/xjtuxb201405010

2013-09-25。 作者简介: 许大涛(1988-),男,硕士生;冯慧华(通信作者),男,副教授,博士生导师。 基金项目: 国家自然科学基金资助项目(51006010);高等学校学科创新引智计划资助项目(B12022)。

时间: 2014-02-26 网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140266.1159.016.html

TK441

:A

:0253-987X(2014)05-0056-05