超临界水通道内压降特性分析
徐 莉,臧金光,2,曾小康,闫 晓
(1.中国核动力研究设计院 中核核反应堆热工水力技术重点实验室,四川 成都 610041;
2.清华大学 工程物理系,北京 100084)
在反应堆中,堆芯释放的热量由系统回路中的冷却剂带出,堆芯的输热能力与冷却剂的流动特性密切相关,堆芯内冷却剂的流量分配对堆芯冷却剂温度场、燃料元件表面温度分布均有重要影响。在热工水力设计的过程中,应尽量使冷却剂的流量分布与堆芯功率分布相匹配,以最大限度地提高反应堆的运行功率,同时保证反应堆的安全性。分析冷却剂的压降特性是堆芯热工水力设计的重要方面[1]。
超临界水冷堆是利用超临界状态下的水作为冷却剂和慢化剂的第4代核能系统[2]。超临界条件下由于存在剧烈的物性变化,压降特性具有自身的特点。超临界水在拟临界点前后密度有较大落差,重力压降需考虑密度的沿程积分效应,同时密度的明显变化使得加速压降相比亚临界条件下更为明显。在等温条件下,摩擦系数均为雷诺数的单值函数;而在加热条件下,近壁面边界层处的流体物性与主流体物性的差别较大,摩擦系数的计算需考虑近壁面处的物性修正。超临界条件下的摩擦关系式多以亚临界条件下的关系式为基础加以扩展。
本文对超临界条件下的流动特性进行研究。
1 压降类型
一般而言,通道内的流动压降可分为加速压降、重力压降、摩擦压降和局部压降,本文着重分析加速压降、重力压降和摩擦压降在超临界条件下的变化规律。
在超临界条件下,拟临界区附近的密度变化较为剧烈,计算重力压降时不能简单认为密度为常数,需考虑密度的沿程积分效应。

(1)
其中:ρ为流体密度;g为重力加速度;Δpg为重力压降;θ为流道与竖直方向的倾角;L为流动距离;x为积分变量。
采用目前成熟的数值积分方法[3]对式(1)求解,如应用较广泛的Newton-Cotes求积公式:

(2)
其中:xi为求积节点;n为积分阶数;Ai为求积系数,定义式如下:

(3)
其中:li(x)为拉格朗日插值基函数;a、b为积分上、下限。
当n=1时,式(2)为梯形求积公式:

h=b-a
(4)
当n=2时,式(2)为辛普森求积公式:

h=(b-a)/2
(5)
当n=3时,式(2)为牛顿求积公式:

3f(x2)+f(x3))h=(b-a)/3
(6)
其中,xi=a+ih。
以辛普森求积公式计算重力压降为例:


(7)
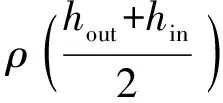
除以上数值积分方法外,也有研究者建议采用其他方法,如Ornatskiy等推荐采用焓值平均来考虑密度的积分效应[4]:

(8)
为衡量这些积分表达式间的区别,分别用以上方法计算了压力为25 MPa下不同焓值区间的平均密度,其中精确值采用精确分段法,将焓值的积分区间划分50个节点,再线性平均后得到。图1示出不同焓值区间下的平均密度,其中工况编号1~5分别代表焓值区间为1 850~2 000、1 850~2 200、1 850~2 400、1 850~2 600和2 300~3 000 kJ/kg。由图1可见:当焓值区间较小时,密度变化较小,采用不同方法计算的结果相差不大;当焓值区间逐渐扩大时,梯形求积法差异最大,最大相对误差达11%,而辛普森求积法的最大相对误差为0.9%,牛顿求积法的最大相对误差为0.6%,Ornatskiy法的最大相对误差为1.2%[4]。大部分情况下,采用Ornatskiy法计算密度的平均值是合理的,也易于实现。辛普森求积法在计算精度上较Ornatskiy法好些,但需多调用一次物性函数。

图1 不同焓值区间的积分方法比较
亚临界条件下,计算单相流的摩擦压降Δpf普遍采用Darcy公式[1]:

(9)
其中:f为Darcy-Weisbach摩擦系数;Δz为单位通道长度;De为通道水力直径;v为流体平均速度;G为质量流速。
加速压降Δpa的计算公式为:
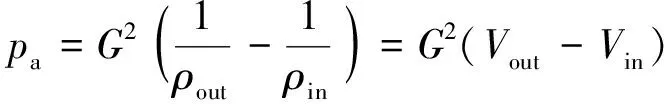
(10)
式中:ρout、ρin分别为通道出口和入口的流体密度;Vout、Vin分别为相应位置的比体积。

图2 不同压降梯度的沿程变化
图2示出用CFX计算的光滑2×2棒束结构各项压降梯度的对比。由图2可见,加速压降梯度与摩擦压降梯度沿程一直增大,而重力压降梯度沿程一直减小。由3项压降梯度的定义式可知,重力压降梯度与平均密度呈正比,摩擦压降梯度与流体密度呈反比,加速压降梯度与流体比体积的落差呈正比。在整个加热过程中,单位通道长度上的流体密度随温度的升高而下降,比体积上升,导致加速压降梯度和摩擦压降梯度增大和重力压降梯度减小。在通道入口区,重力压降梯度最大,其次是摩擦压降梯度;之后,摩擦压降梯度逐渐增大,而重力压降梯度逐渐减小,使得前者慢慢超过后者。
图3示出绝热条件(冷态)和加热条件(热态)下各项压降梯度的对比。绝热条件下,加速压降梯度为零。由图3可见:摩擦压降梯度和重力压降梯度一直维持不变;加热后,由于沿程物性的变化,加速压降梯度产生,且沿程逐步增大;重力压降梯度相比绝热条件时减少,沿程伴随密度的下降而下降;摩擦压降梯度比绝热条件时略有增加。加热后总压降梯度比绝热条件时的略有上升。实际堆芯设计中,由于堆芯内结构复杂,棒束通道和通道阻塞物很多,加上在超临界条件下冷却剂温度要跨过拟临界区,因此可能会使堆芯内的压降变化很大。这是进行超临界条件流动实验时必须要考虑的问题。

图3 冷态与热态时不同压降梯度的沿程变化
2 亚临界单相摩擦关系式
超临界条件下的摩擦关系式多以亚临界单相摩擦关系式为基准,再辅以壁面物性与主流体物性之比作为修正,其优点在于当壁面温度与主流体温度之差较小时,摩擦关系式能自然过渡到正常等温条件。因此,发展超临界条件下的摩擦关系式需选取一合适的亚临界等温摩擦关系式为基础。
亚临界条件的等温摩擦关系式中适用范围较广及预测精度较高的关系式之一是经典的隐式PKN公式(式(11)),它是由Prandtl等根据大量实验测量结果得到的一半理论、半经验关系式[5],与大量实验数据具有较好的一致性。
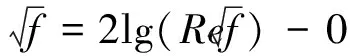
(11)
隐式PKN公式计算较为复杂,需不断迭代,用于发展超临界条件下摩擦公式时会有些不便。基于隐式PKN公式形式,通过简单数学推导,可得到PKN公式的显式形式。显式PKN公式在精度与适用范围上与隐式PKN公式相当,同时免去了复杂的迭代过程。显式PKN公式是将Blausius公式代入隐式PKN公式,经化简整理,得:
f=1/(1.75lgRe-1.3)2
(12)
为便于分析比较,选取其他几个常用公式作为比较。
McAdams公式:
f=0.184Re-0.2
(13)
Blausius公式:
f=0.316 4Re-0.25
(14)
Filonenko公式:
f=1/(1.82lgRe-1.64)2
(15)
为验证推导的显式PKN公式与隐式PKN公式的接近程度,同时比较各摩擦系数公式的预测性能,分别计算了它们在不同雷诺数范围内的摩擦系数,结果示于图4。由图4可见:当雷诺数较小时,McAdams公式的计算结果明显小于隐式PKN公式的,随着Re减小,误差增大;当
Re较高时,McAdams公式的计算结果逐渐与隐式PKN公式的接近,可见McAdams公式主要适用于高Re范围;在所考察的Re范围内,Blausius与Filonenko公式的计算结果均与隐式PKN公式的接近,只是在Re较小时,Filonenko公式的计算结果略大于隐式PKN公式的,Blausius公式的计算结果则略小;而本文推导的显式PKN公式的计算结果在整个Re范围内均与隐式PKN公式的最接近。这可从推导的过程中看出,显式PKN公式是将Blausius公式作为初值代入隐式PKN公式获得的,Blausius公式本身具有相对较好的预测性能,经过隐式PKN公式的迭代修正后,会更接近于隐式PKN公式,这是它比其他公式预测性能更好的原因。图5示出各摩擦关系式计算结果的区别。
3 超临界摩擦关系式
针对超临界条件下流动实验的研究目前还不充分,缺少较普遍认可的摩擦关系式,对其中的机理仍有待于进一步研究。
以下是一些研究者基于实验数据拟合出的超临界条件下的摩擦关系式[4]。
Mikheev公式:
f=fiso(Prw/Prb)1/3
(16)
其中:fiso为等温流动摩擦系数;Prw、Prb分别为以壁面温度和主流体温度为特征温度得到的流体普朗特数。
Popov公式:
/ρb)0.74
(17)
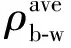

图4 各摩擦关系式计算结果比较

图5 各摩擦关系式计算结果的差异
Kondrat’ev公式:
f=0.188Re-0.22
(18)
Kirillov公式:
f=fiso(μw/μb)0.4
(19)
其中,μw和μb分别为壁面和主流体的动力黏度。
上述公式中的fiso均采用Filonenko公式计算。鉴于实验数据不充分,本文利用CFD方法比较了这几组基于实验的摩擦关系式与数值结果的差异。选取Mokry等[6]开展的超临界条件下竖直圆管的传热实验为参考,管长为4 m,
直径为10 mm,质量流速G为203~1 495 kg/(m2·s),热流密度q为335~884 kW/m2,实验工况列于表1。

表1 实验工况
以Fluent软件为计算平台,ICEM为几何建模和网格划分工具,生成二维四面体结构化网格。合理控制边界层的网格参数,使第1层网格的y+<1,同时开展网格的无关性分析,确保计算结果不依赖于网格参数。入口采用定速度边界条件,给定入口温度;出口设置相对静压值为零,组件盒采用无滑移绝热壁面边界条件;元件棒表面依据计算工况不同设置定热流密度边界条件。计算时选用SST湍流模型。
图6示出不同摩擦关系式与Fluent数值结果沿程预测性能的比较。由图6可见,各摩擦关系式呈现较大的分散性。仔细分析这些关系式的变化趋势可发现:大部分超临界条件加热工况下的摩擦系数均小于亚临界条件等温工况下的摩擦系数,Filonenko关系式是亚临界下的摩擦关系式,整体预测数值最高;超临界加热工况下,壁面温度会远高于主流体温度,近壁面处流体的黏性和密度均小于主流体的黏性和密度,导致摩擦系数变小。这与大部分摩擦关系式的修正方向是一致的。

图6 Fluent与各关系式计算结果的比较
在拟临界点附近,动力黏度迅速下降,通道流体平均雷诺数上升,摩擦系数下降;同时,当壁面温度超过拟临界点、而主流体温度仍低于拟临界点时,近壁面处的物性效应明显,加速了摩擦系数下降的趋势。这是一些关系式计算的摩擦系数在拟临界点处迅速下降的原因。在拟临界点之后,流体温度远离拟临界点区域,壁面流体物性与主流体物性相差较小,物性效应减弱,此时摩擦系数回升。拟临界点处摩擦系数的极小值现象是超临界条件下的独有规律[7]。
在所比较的几组超临界摩擦关系式中,Kirillov公式与Fluent的计算结果较为一致,在分析的4组工况中,随着质量流速和热流密度的变化,二者的吻合程度均较好,包括拟临界点处的摩擦系数谷值,只是在入口区Kirillov公式的计算结果略低于Fluent的计算结果,这可能与CFD数值工具在模拟时考虑了入口效应有关。图7示出Kirillov公式与Fluent计算结果的比较,二者的相对偏差在±10%以内。
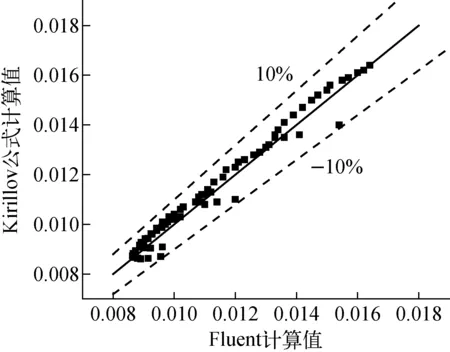
图7 Fluent与Kirillov公式计算结果比较
4 结论
本文分析了超临界条件下剧烈的物性变化对通道内压降特性的影响,得到以下结论。
超临界条件下,拟临界区前后的密度变化剧烈,使得通道内的加速压降不可忽略,重力压降需考虑密度的沿程积分效应。本文比较了不同方法的计算精度,发现梯形求积公式误差较大,Ornatskiy公式采用焓值平均可有效改善精度,辛普森求积公式与牛顿求积公式的精度较好。
基于隐式PKN公式形式和Blausisu公式得到了显式PKN公式,计算精度与隐式PKN公式接近,而在具体求解时又免去隐式PKN公式迭代求解的繁琐,适用于工程上的计算分析。
借助于Fluent的数值分析结果,比较了超临界条件下不同摩擦关系式的异同,发现物性效应修正会使拟临界点附近出现局部极值点,且Kirillov公式与Fluent的计算结果较为一致,相对偏差在±10%以内。
参考文献:
[1] 于平安,朱瑞安,喻真烷,等. 核反应堆热工水力学[M]. 上海:上海交通大学出版社,2002.
[2] OKA Y, KOSHIZUKA S, ISHIWATARI Y, et al. Super light water reactors and super fast reactors[M]. New York: Springer, 2010.
[3] 邓建中,刘之行. 计算方法[M]. 西安:西安交通大学出版社,2007.
[4] PIORO I L, DUFFEY R B. Heat transfer and hydraulic resistance at supercritical pressures in power-engineering applications[M]. New York: ASME Press, 2007.
[5] KAKAÇ S, SHAH R K, AUNG W. Handbook of single-phase convective heat transfer[M]. New York: Wiley-Interscience, 1987.
[6] MOKRY S, PIORO I L, KIRILLOV P, et al. Supercritical-water heat transfer in a vertical bare tube[J]. Nuclear Engineering and Design, 2010, 240: 568-576.
[7] LEI X L, LI H X, YU S Q, et al. Study on the minimum drag coefficient phenomenon of supercritical pressure water in the pseudocritical region[C]∥ICONE20-POWER2012. California, USA: [s. n.], 2012.

