轴向非均匀加热对并联通道流动不稳定性的影响
鲁晓东,周铃岚,巫英伟,苏光辉,秋穗正,张 虹
(1.西安交通大学 动力工程多相流国家重点实验室,陕西 西安 710049;
2.西安交通大学 核科学与技术系,陕西 西安 710049;
3.中国核动力研究设计院 核反应堆系统设计技术重点实验室,四川 成都 610041)
两相流动不稳定性现象广泛存在于工业系统和设备中,例如蒸汽发生器、沸水堆和制冷装置等。它会引起系统流量和压力振荡,致使系统装置发生机械振荡影响系统控制,危害系统安全。因此在系统设计和运行时,需避免流动不稳定性现象的发生。在过去的几十年中,对两相流动不稳定性进行了大量的实验研究和数值计算。近年来,许多学者[1-4]将目光投向了并联通道两相流动不稳定性的研究。在并联系统中,各通道具有相同边界条件,相互间存在影响。当某个通道发生扰动时,另外的通道也会受到影响,这使并联通道两相流动不稳定性的研究特别复杂和困难。在已有的研究中,广泛采用轴向均匀加热的假设来研究并联通道系统流动不稳定性。然而,在真实的核反应堆系统中,堆芯轴向功率分布是非均匀的。因此,为更加真实地研究反应堆系统中的两相流动不稳定性现象,本文选取余弦功率加热计算系统的稳定性边界和三维不稳定性空间,以研究轴向非均匀加热对并联通道两相流动不稳定性的影响。
1 物理模型和数值解法
1.1 系统结构
在本研究中,将反应堆堆芯系统简化为由上下联箱和中间两个通道组成的系统,如图1所示。为更好地分析问题,本文作如下假设:1) 两相区采用均相流模型;2) 入口流体过冷;3) 两相流体处于热力学平衡状态;4) 忽略过冷沸腾。
1.2 物理模型
对于均相流模型,单相区和两相区的控制方程均可写成如下形式。
质量守恒方程:
(1)
动量守恒方程:
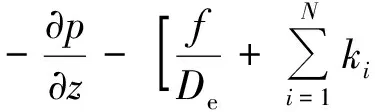
(2)

图1 并联通道系统简图
能量守恒方程:
(3)
状态方程:
ρ=ρ(p,h)
(4)
式中:p为压力;h为流体焓;ρ为流体密度;u为流体流速;A为流体流动截面积;De为当量直径;f为摩擦系数;ql为线功率;z为坐标轴方向;ki为节流系数;δ为Dirac函数。
式(4)两边分别对时间t求导,可得:
··
(5)
将式(5)分别代入式(1)和式(3),得:
··(ρu)=0
(6)
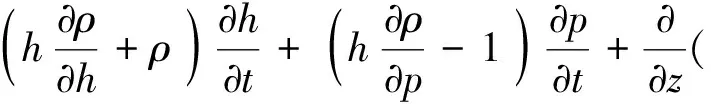
(7)
在计算压降时,需选择适当的f和两相摩擦倍增因子Φ2。表1列出单相区摩擦系数f1φ,两相区摩擦系数f2φ为:
Φ2
(8)
Φ2采用MaAdams模型,即:
(9)

表1 摩擦系数关系式
1.3 数值方法
空间上采用交错网格技术,即将系统的p、h、ρ等物性参数储存在控制体中心(如图2中虚线位置),将u存放于控制体边界处(如图2中实线位置),从而可省略同位网格技术中的迭代步骤,提高计算速度。在时间上采用半隐式差分方式进行离散,避免了完全隐式差分求解困难和耗时的缺点。当界面速度大于零时,边界处流体物性参数取来流方向上最后1个控制体中心的值[5]。
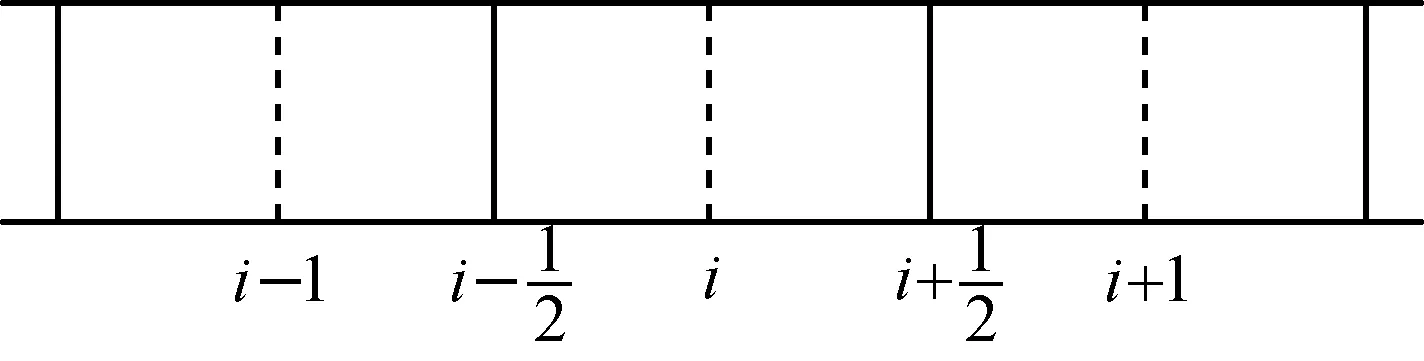
图2 一维空间网格
根据图2的空间控制体划分方式,在第i个控制体处对式(6)、(7)进行离散,可得:
·
(10)

(11)
(12)
上述3组差分离散方程求解时是封闭的。当时间步长满足Δt<Δz/u时,上述方程采用的离散格式稳定且精确。
(13)
其中:
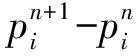
1.4 分析方法
由于入口段和上升段对并联通道两相流动不稳定性均有影响[4],为更好地研究轴向非均匀加热对流动不稳定性的影响,本文将不考虑入口段和上升段。在计算不稳定边界时,采用小扰动法进行研究,即在并联通道系统处于稳定状态时,对其中1根通道的加热量在极短时间(1 s)内给定一微小扰动(增加或减小1%),系统运行一段时间后,观察两个通道的流量脉动曲线和相空间轨迹,判断系统所处的运行状态。
当进口温度相同时,随加热功率的增加,流量脉动依次经历阻尼振荡、极限环振荡和发散振荡,如图3所示,图中Npch为相变数、Nsub为进口过冷度数。选取极限环振荡时的加热功率为临界功率,并以此获得不稳定性边界。
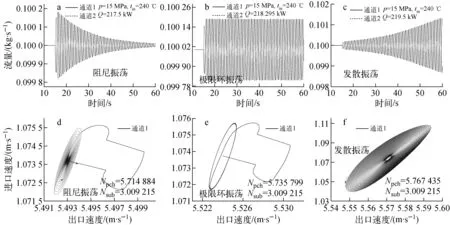
图3 入口流量振荡曲线(a、b、c)和相空间轨迹(d、e、f)
2 模型验证
本文采用双矩形通道实验结果[6]对模型进行验证。本模型Npch的计算值和实验值的比较结果如图4所示。从图4可看出,本模型计算结果与实验结果的相对误差均在15%以内,说明本文计算结果和实验结果符合良好。但由于本文采用均相流模型,忽略了相间滑移,因此计算结果偏保守。
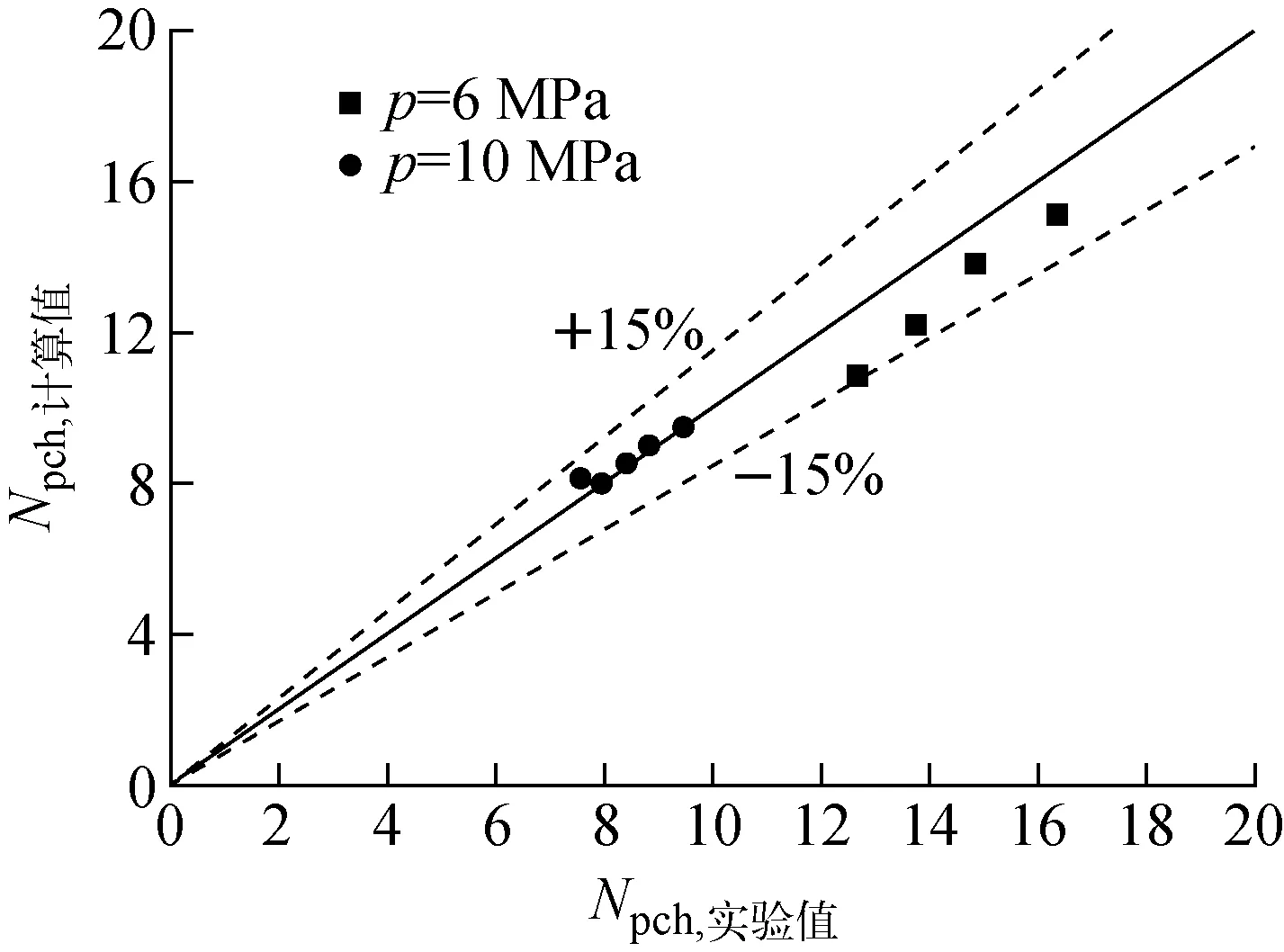
图4 Npch计算值与实验值的对比
3 结果分析
表2列出并联通道的详细参数。本文采用轴向余弦功率加热模拟轴向非均匀功率加热,将均匀功率加热作为参考功率分布,如图5所示。

表2 并联通道详细参数
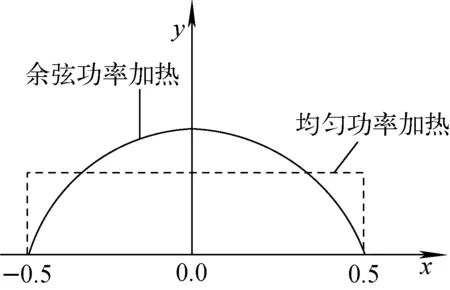
图5 不同的加热功率方式
3.1 不稳定性边界
本文采用进口过冷度数和相变数表征并联通道系统的不稳定边界,定义如下:
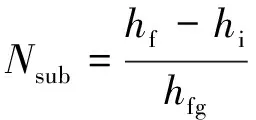
(14)
式中:hf和hg为饱和液体和饱和蒸汽焓;hi为进口液体焓;vfg为饱和蒸汽与饱和液体比体积之差;vf为饱和液体比体积;hfg为汽化潜热;Q为加热量;W为流量。
在以前的文献中,只有少量基于实验数据研究轴向非均匀加热对两相系统稳定性的影响,但存在两种截然相反的结论。Djikman等[7]发现余弦功率加热可增强系统的稳定性;然而Bergles[8]则认为余弦功率加热会降低系统的稳定性。采用本文所得的图6,可很好地解释这两种结论。

图6 余弦功率加热对系统稳定性的影响
图6为7 MPa下余弦功率加热对系统稳定性的影响。从图6可看出,在高过冷度区,余弦功率加热的系统稳定性边界(MSB)相对于均匀功率加热的MSB向左移动,系统稳定性降低。但在低过冷度区,余弦功率加热的MSB向右移动,余弦功率加热增强了系统稳定性。在不同的系统压力下,可得到相似结论,如图7所示。
产生上述现象的原因如下:对于两相系统,单相段压降对系统的稳定性起着很重要的作用。单相段压降越大,系统越稳定。对于余弦功率加热和均匀功率加热,在高过冷度区,沸腾边界均处于通道的上半区,但余弦功率加热时沸腾边界较均匀功率加热时低,单相段压降相对较低,因此系统稳定性降低。在低过冷度区,对于上述两种加热方式,通道的沸腾边界均发生在下半部,而余弦功率加热的沸腾边界较均匀功率加热的高,单相段压降相对较大,因此系统稳定性增强。

图7 系统的MSB
3.2 三维不稳定性空间
从图7可看出,二维的MSB并不能清楚地显示压力对系统稳定性的影响。Guo等[4]在2008年提出的不稳定性空间(不稳定岛)的概念解决了这个问题。在本研究中,采用由Npch、Nsub和无量纲压力(p+=p/10patmosphere)组成的三维空间来研究不同加热方式下的系统稳定性。
本文计算了余弦和均匀功率加热在压力为7、9和15 MPa下的并联通道MSB,获得了相应加热方式下的不稳定性空间,如图8所示。从图8可看出,对于余弦和均匀功率加热,随系统压力的增加,不稳定性区域均逐渐变小,并联通道系统的稳定性增强。
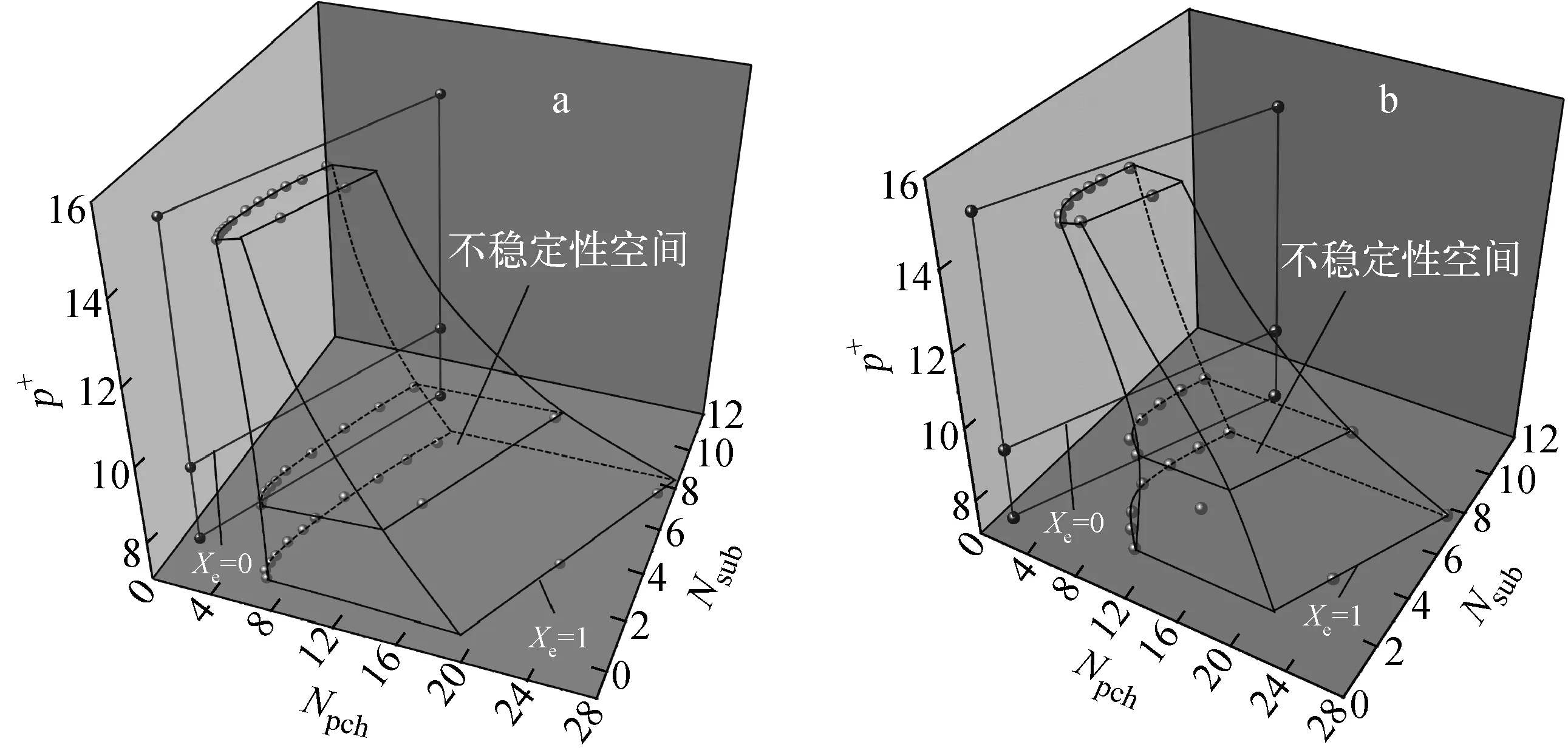
图8 均匀功率(a)和余弦功率(b)加热的不稳定性空间
3.3 进口阻力系数的影响
对于均匀功率加热的系统,已有很多学者研究了进口阻力系数对系统稳定性的影响。然而对于余弦功率加热的系统,这方面的研究却进行得很少。因此本文研究了余弦功率加热时进口阻力系数kin对并联通道系统稳定性的影响,如图9所示。从图9可看出,系统稳定性随进口阻力系数的增大而增强。因增加进口阻力系数增大了单相段压降,从而增强了系统稳定性。此外,从图9还可知,随进口阻力系数的增大,MSB的拐点逐渐向高过冷度移动。

图9 进口阻力系数对系统稳定性的影响
4 结论
1) 余弦功率加热对系统稳定性的影响在不同的过冷度区域表现为不同的形式:在高过冷度区,降低系统的稳定性;在低过冷度区,增强系统的稳定性。
2) 无论是余弦功率加热还是均匀功率加热,系统压力均会增强并联通道系统的稳定性。
3) 当系统处于余弦功率加热时,进口阻力系数能增强系统的稳定性。同时,随进口阻力系数的增大,MSB的拐点逐渐向高过冷度区移动。
参考文献:
[1] MUNOZ-COBO J L, PODOWSKI M Z, CHIVA S. Parallel channel instabilities in boiling water reactor systems: Boundary conditions for out of phase oscillations[J]. Annals of Nuclear Energy, 2002, 29(16): 1 891-1 917.
[2] LEE J D, PAN C. Dynamics of mutiple parallel boiling channel systems with forced flows[J]. Nuclear Engineering and Design, 1999, 192(1): 31-44.
[3] ZHANG Y J, SU G H, YANG X B, et al. Theoretical research on two-phase flow instability in parallel channels[J]. Nuclear Engineering and Design, 2009, 239(7): 1 294-1 303.
[4] GUO Y, QIU S Z, SU G H, et al. Theoretical investigations on two-phase flow instability in parallel multichannel system[J]. Annals of Nuclear Energy, 2008, 35(4): 665-676.
[5] Office of Nuclear Regulatory Research. RELAP5/MOD3.3 code manual volume Ⅵ: Validation of numerical techniques in RELAP5/MOD3.3[M]. US: Nuclear Regulatory Commission, 2001: 53-62.
[6] LU D H, LI H B, CHEN B D, et al. Experimental study on the density wave oscillation in parallel rectangular channels with narrow gap[J]. Annals of Nuclear Energy, 2011, 38(10): 2 146-2 155.
[7] DJIKMAN F J M, SLUITER M L C. One-channel non-linear digital model for boiling water hydrodynamics[J]. Nuclear Engineering and Design, 1971, 16(3): 237-248.
[8] BERGLES A E. Review of instability in two phase systems[C]∥KAKAC S, MAYINGER F. Two Phase Flow and Heat Transfer. New York: NATO Advanced Study Institute, 1976.

