超强台风下导管架平台结构弹塑性分析*

朱本瑞 陈国明 刘红兵 林 红 黄 超 张 坤

(中国石油大学(华东)海洋油气装备与安全技术研究中心)

超强台风下导管架平台结构弹塑性分析*

朱本瑞 陈国明 刘红兵 林 红 黄 超 张 坤

(中国石油大学(华东)海洋油气装备与安全技术研究中心)

针对超强台风引起的导管架平台甲板上浪载荷,基于三线性上浪载荷时间历程,采用API模型与Stokes 5 th波理论建立了上浪载荷计算方法与流程。在此基础上,应用静力推覆分析方法考察了不同上浪高度下导管架平台结构承载能力与失效模式的变化规律,利用动力弹塑性分析方法探讨上浪高度对导管架平台结构动态特性的影响,结果表明:上浪载荷导致导管架平台极限承载能力降低,当上浪达到一定高度时,平台失效模式由桩基失效演变为导管架顶部失效;平台在弹性和塑性阶段均存在一定程度的动力放大效应,且塑性响应阶段的动力放大效应更加显著。本文研究成果可为我国深水导管架平台的安全评估与优化设计提供参考。

超强台风;导管架平台;甲板上浪载荷;静力推覆分析;动力弹塑性分析;动力放大系数;失效模式

0 引言

超强台风引起的波浪载荷是海洋平台倒塌破坏的主要原因,美国矿产管理局研究报告显示,2002—2005年台风Lili、Ivan、Katrina和Rita相继摧毁的122座导管架平台中大部分是由波浪引起的过载造成的[1-3]。超强台风引起的波浪载荷除本身巨大的作用力外,其引起的巨幅波峰有可能导致甲板上浪,从而对平台上部组块形成巨大的冲击载荷[4]。目前,国外围绕导管架平台上浪载荷的数值模拟、波浪水槽实验等方面进行了大量研究[5-9],其中文献[8]率先考虑了平台结构的非线性,采用简化的单自由度方法对上浪载荷下导管架平台的弹塑性响应进行了分析;文献[9]提出的增量波方法分别从静态和动态角度评估了平台结构的极限承载能力,这些成果为开展超强台风引起的波浪荷载作用下导管架平台的性能评估奠定了基础;而国内针对导管架甲板上浪载荷下平台结构弹塑性动力分析等方面的研究均未见报道。为此,本文以某深水导管架平台为例,首次考虑甲板上浪载荷及其动态特性,分别采用静力推覆分析与动力弹塑性时程分析方法对平台在超强台风引起的波浪荷载作用下的承载性能和力学特性进行了考察,其研究成果可为我国导管架平台结构的设计与性能优化提供参考。

1 超强台风下导管架平台结构波浪载荷计算

1.1 作用于导管架上的波浪载荷

导管架构件尺寸与波长相比一般较小,对于这类小尺度杆件上的波浪载荷,截至目前仍采用Morison公式来描述,即

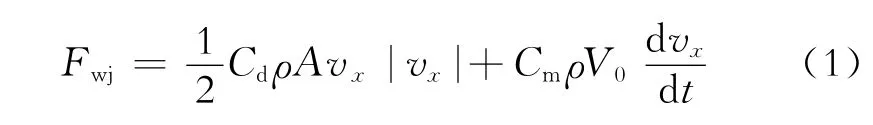
式(1)中:Fwj为作用于导管架构件上的波浪载荷, N;vx为杆件轴中心位置任意高度处波浪水质点的水平速度,m/s;t为时间,s;A为单位杆件垂直于波向的投影面积,m2;V0为单位杆件的排水体积, m3;ρ为海水密度,kg/m3;Cd为拖曳力系数;Cm为惯性力系数。

对于超强台风环境下,由于波陡较大,波面高度η和水质点水平速度vx应采用非线性波浪理论进行描述[10]。采用Stokes 5 th波理论时两者的计算公式分别为

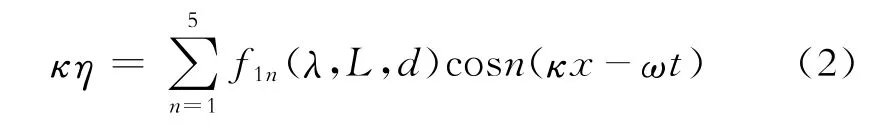
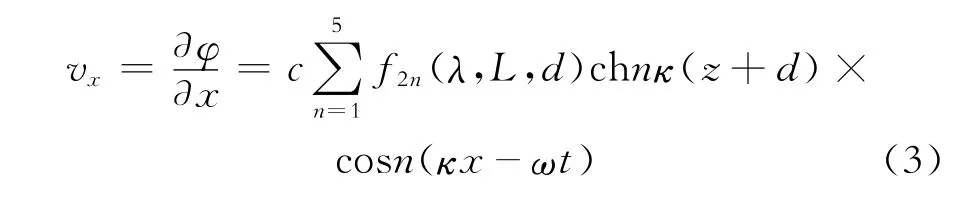
式(2)、(3)中:κ为波数;λ为波浪系数;L为波长, m;d为水深,m;x为水质点的位移,m;ω为圆频率, rad/s;φ为速度势;c为波速,m/s;z为水质点距离海面的高度,m;f1n和f2n为关于系数λ、波浪L和水深d的函数,n=1,2,3,4,5;其他参数意义同前。

1.2 作用于甲板上的上浪载荷

1.2.1计算模型

迄今为止,对甲板上浪载荷的计算尚没有普遍认可的方法。现有的方法大致可分为侧面轮廓法和细节构件法两大类。其中,侧面轮廓法包括API模型、DNV拍击力模型、SHELL模型和MSL模型等,各种模型的详细讨论可参考文献[11]。采用API模型[12]计算甲板上浪载荷时,其公式为

式(4)中:vuc为与波浪同向的流速,m/s;awkf为波浪运动系数,台风时取0.88;acbf为导管架的海流阻挡系数;A=zwd×b(zwd为波浪淹没甲板的高度,m;b为甲板宽度,m),为甲板淹湿轮廓在波浪方向的投影面积,m2;其他参数意义同前。

计算甲板上浪的关键在于确定甲板淹湿位置处的波面高度及水质点水平速度,可根据Stokes 5 th波理论建立的色散关系方程组,并采用牛顿法编程求解出波长L和系数λ,然后代入波面公式(2)和速度公式(3)计算得到[13]。

1.2.2动态特性

甲板上浪载荷具有动态特性,然而至今对其载荷历程尚无统一的认识。文献[5]和文献[6]采用波浪水槽和计算流体动力学(CFD)技术对甲板上浪载荷进行了物模实验和数值仿真;文献[11]在前者实验的基础上提出了上浪载荷简化时间历程模型(即三线性模型),并对其关键参数进行了敏感性分析,证实了该模型的适用性。三线性上浪载荷简化时间历程如图1所示,其中Fdmax为甲板上浪载荷极大值,定义为上浪高度最大时对应的载荷,可由公式(4)计算得到;twd为上浪载荷作用总时间,定义为从波浪前沿接触平台底层甲板至最终与甲板完全分离的时间;t1、t2、t3分别为不同上浪阶段对应的作用时间,其比值为0.5∶0.5∶2.1。本文采用该模型对平台动态响应进行分析。

图1 甲板上浪载荷时间历程简化模型

2 超强台风下导管架平台结构弹塑性分析

2.1 分析方法原理

2.1.1静力推覆分析方法

静力推覆分析是进行结构极限承载能力分析最有效的一种方法[14-15],目前API、ISO以及DNV等规范普遍推荐使用该方法。该方法是对平台施加环境载荷,考虑结构与几何非线性因素,采用增量方式对环境载荷进行逐级放大,直至平台发生倒塌,然后通过平台抗力曲线对其在不同阶段的响应和承载性能进行评估。静力推覆分析方法原理如图2所示,其中,Fy为平台构件首次进入屈服时对应的环境载荷,N;Fult为平台倒塌时对应的极限载荷,N;uy和uult分别为Fy和Fult对应的位移,m。

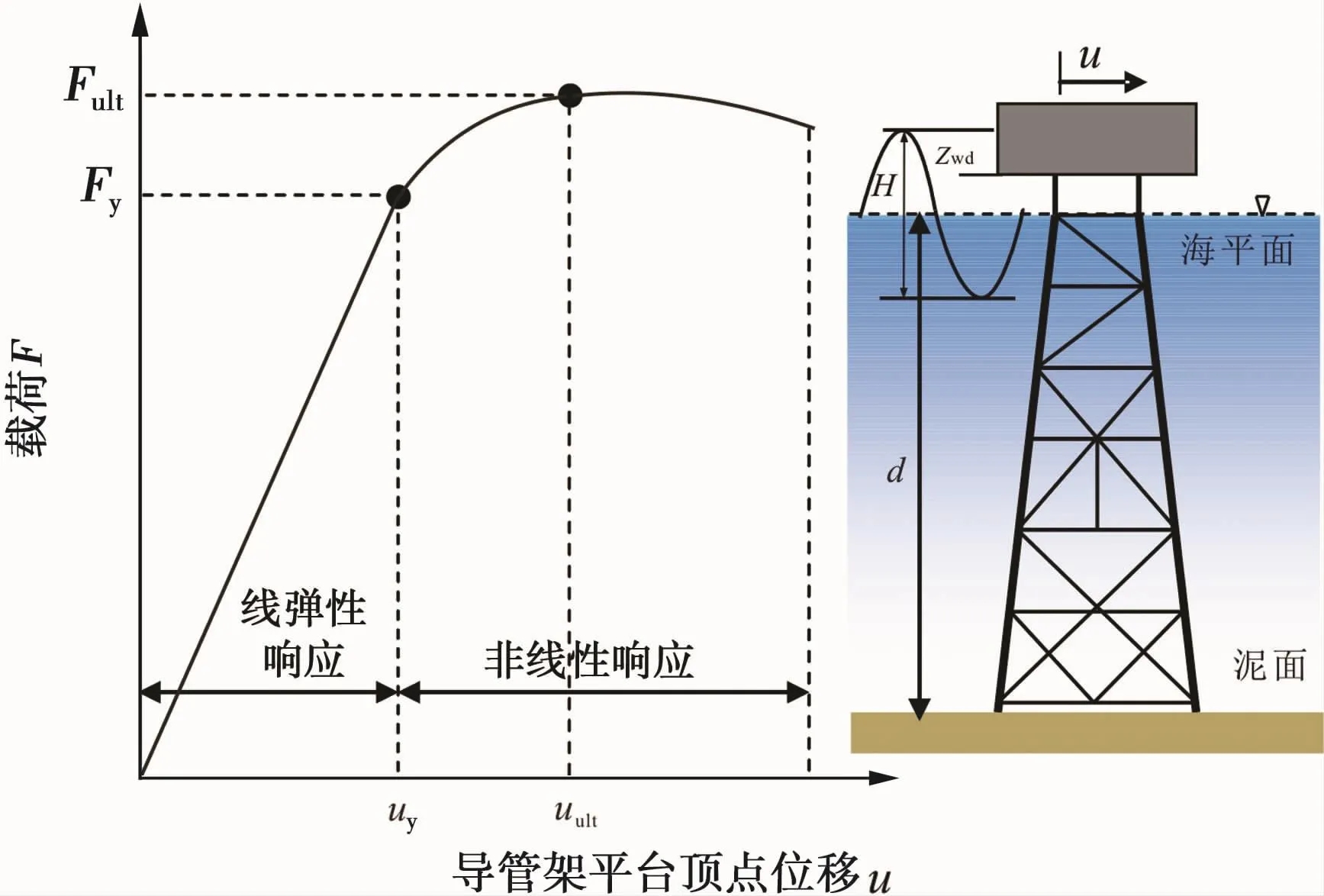
图2 导管架平台静力推覆分析方法原理图

2.1.2动力弹塑性分析方法

动力弹塑性分析是一种精确的分析方法,该方法综合考虑了结构几何与材料非线性以及环境载荷的动力特性,可以有效评估平台的动态响应,确定其动力放大系数DAF(Dynamic Amplification Factor)。DAF定义为平台非线性动力分析的最大位移响应umax与同等载荷下静力推覆分析计算位移ueq的比值。平台动态位移响应可通过其离散化的动力方程求得,即

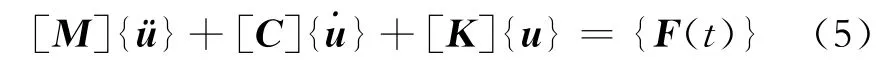
对于非线性系统,求解方程(5)时,由于结构刚度矩阵不断变化,节点位移未知量需要采用增量法或迭代求得。应用ANSYS有限元软件计算时,其瞬态分析模块提供了Newmark和HHT-α两种积分方法。其中,HHT-α是一种改进的Newmark法,该方法通过引进数值耗散函数α,并将动力平衡方程表示为两个相邻时间积分步的线性组合,从而提高了计算的精度和稳定性[16],因此本文选用该方法进行计算。此外,分析结构动力响应时应计入阻尼的影响,文中采用Rayleigh阻尼进行考虑[17]。

2.2 有限元模型与分析工况

2.2.1有限元模型

某海洋导管架平台设计水深107 m,导管架由7层构成,4根腿柱为双斜对称结构,其中ROW A和ROW B面斜撑为K型布置,ROW1和ROW2面由K型和对角斜撑组成;平台上部组块尺寸为45 m× 45 m,质量6 033 t(包括设备质量),底层甲板高程为16.5 m;导管架采用4组12桩安装于海底,桩腿入泥深度为99.75 m。

考虑到导管平台结构弹塑性分析涉及到结构非线性力学行为的研究,建模时应充分考虑模拟单元的力学特性及材料非线性。本文分别选用3D弹塑性单元PIPE288和PIPE20单元建立平台导管架与桩腿部分,其中PIPE288单元可通过SOCEAN模块自动模拟计算波浪载荷;上部组块采用线弹性单元PIPE16建立;桩-土非线性相互作用采用弹簧单元COMBIN39模拟,弹簧实常数通过平台井位处土层设计强度参数计算得到的p-y曲线、t-z曲线以及桩端q-z曲线定义;设备质量采用MASS21单元模拟。鉴于导管架平台结构复杂,非线性动力分析需要大量计算时间,故计算过程中仅考虑桩腿和导管架结构的非线性(包括几何与材料非线性),上部组块结构则进行简化,并将其材料属性设置为线弹性,如图3所示。

图3 某海洋导管架平台有限元模型

2.2.2分析工况

2386 已知A1E1、A2E2是⊙O的两条弦，且A1E1∥A2E2，A1E1=A2E2，直径BF⊥A1E1于O1，交A2E2于O2，点C在上，CA1、CA2分别交直径BF于点P1、P2，BC交A1E1于Q1，交A2E2于Q2．

某导管架平台所处海域100年一遇最大波高为17.1 m,周期为12.4 s,风速为43.6 m/s,表面流速为1.901 m/s,风暴潮为3.08 m;偶然灾害条件下(10 000年一遇)的最大波高为29 m,风速为56.8.m/s,周期为16 s;表层流速为2.355 m/s,水深5 m处流速为1.817 m/s,海底流速为0.390 m/s。为研究平台塑性阶段的力学特性,本文分析工况取偶然灾害条件,根据文献[12],对于4桩腿导管架平台,端向(载荷作用方向为0°)时acbf取0.8,甲板类型为中型设备时Cd取2.0,由此计算得到该平台结构的波浪载荷和上浪载荷(表1),其中水深变化引起海流流速的增加根据波剖面线性延伸获得。

由表1可知,随着水深的增加,波面高度ηmax和对应水质点的水平速度vx变化很小,而上浪高度不断增大,从而导致作用于上部组块上的波浪载荷Fdmax逐渐增大,导管架上载荷Fjmax逐渐减小。应注意到,当上浪高度为5.18 m时,上浪载荷达到导管架波浪载荷的1.14倍,可见甲板上浪载荷的冲击力很大。

将该导管架上波浪载荷与甲板上浪载荷的时间历程进行线性叠加,得到不同工况下平台受到的总波浪载荷时间历程,如图4所示。由图4可知,上浪载荷最大值Fdmax发生在4.1 s时,随着水深的增加,上浪载荷作用时间逐渐增大。应注意到,不同工况下,导管架平台受到的总波浪载荷仅在上浪载荷发生时间内的变化较大,而其余时间内的载荷大小几乎相同。

表1 不同工况下某导管架平台波浪载荷极值数据表

图4 不同工况下某导管架平台结构总波浪载荷时间历程

2.3 分析结果

2.3.1静力推覆分析结果

采用静力推覆分析方法对某导管架平台进行非线性静力推覆分析,材料本构关系选用双线性动力硬化模型,定义屈服应力为345 MPa,切线模量为763 MPa;非线性方程求解时应用弧长增量法,由此得到不同工况下该平台承载能力曲线,如图5所示。由图5可知,该平台在上浪高度为0.27 m时(水深107 m),其极限承载能力为93.3 MN,具有较高的抗力水平和刚度;而随着上浪高度的增加,平台结构刚度和极限承载能力逐渐降低,当水深为114 m时,极限承载能力为48.6 MN,相对于水深107 m时降低了48.9%。可见,上浪载荷对导管架平台整体抗力影响较大,设计时应保证甲板高程具有足够的气隙。

图5 不同工况下某导管架平台承载能力曲线

进一步分析该平台结构的失效模式,提取不同上浪高度下的平台结构塑性应变分布,如图6所示(以水深107 m和114 m为例,其他水深计算结果介于两者之间)。由图6可知,水深为107 m时,该平台失效模式主要为桩基和导管架失效,载荷施加方向对侧桩基形成双塑性铰失效模式(如图6a箭头所示),且导管架腿柱A2和B2因承受压弯载荷而发生屈服(如图6a红圈所示)。而水深为114 m时,除导管架腿柱A2和B2发生塑性变形外,该平台塑性区主要分布于导管架顶部(如图6b箭头所示),失效模式演变为上层斜撑与腿柱失效,且导管架顶端与上部组块连接构件均出现塑性变形。不难想象,随着塑性区的不断扩展,该平台上部组块必然会发生倾覆倒塌失效。

图6 不同上浪高度下某导管架平台结构失效模式

2.3.2动力弹塑性分析结果

对某导管架平台施加如图4所示的波浪载荷进行非线性瞬态分析,采用直接时间积分H HT-α算法,并指定非线性求解最优化选项;收敛准则设置为10-3;阻尼比ζ取0.05,质量矩阵阻尼系数和刚度阻尼系数分别为0.121和0.021(通过模态分析获得该平台前两阶固有频率分别为0.379 Hz和0.392 Hz);计算时间取一个波浪周期16 s;载荷加载方式为阶跃加载;设置平台初始时刻速度为零。由此,计算得到该导管架顶点在不同工况下的位移响应,如图7所示。由图7可知,在一个周期波浪载荷作用下,该平台位移响应呈现周期性振动,且随着上浪高度的增加而增大,最大峰值发生在5 s左右,显然这是由于上浪载荷逐渐增大而引起的。但是,水深107～112 m时平台位移响应从第二个峰值以后围绕平衡点(位移接近为0)进行往复振动,而水深在113 m和114 m时振动平衡位置分别为0.11 m和0.47 m附近。而从图4可知,该平台在8 s之后受到的波浪载荷几乎相同,这说明水深在113 m和114 m时平台发生了不可恢复的塑性变形,从而加剧了结构响应的幅值。

图7 不同工况下某导管架顶点水平位移响应

进一步提取该平台甲板顶部的加速度响应,如图8所示。由图8可知,水深为107 m(上浪高度为0.27 m)时平台振动加速度最小,最大值仅为0.21 m/s2,发生在8.8 s;除此之外,其余工况加速度响应最大值均发生在4 s左右,且随上浪高度的增加而增大,首个峰值过后均存在不同程度的衰减。当水深大于112 m时,该平台振动加速度最大值大于2.0 m/s2,已不满足NORSOK S-002[18]规定的可接受极限水平。此外,应注意到水深在114 m时平台加速度最大值为3.22 m/s2,大于所有工况,但首个峰值过后其加速度峰值却小于水深112 m和113 m时的结果,这是因为平台结构塑性变形增加了结构材料的阻尼,从而使得平台的响应变得迟缓。

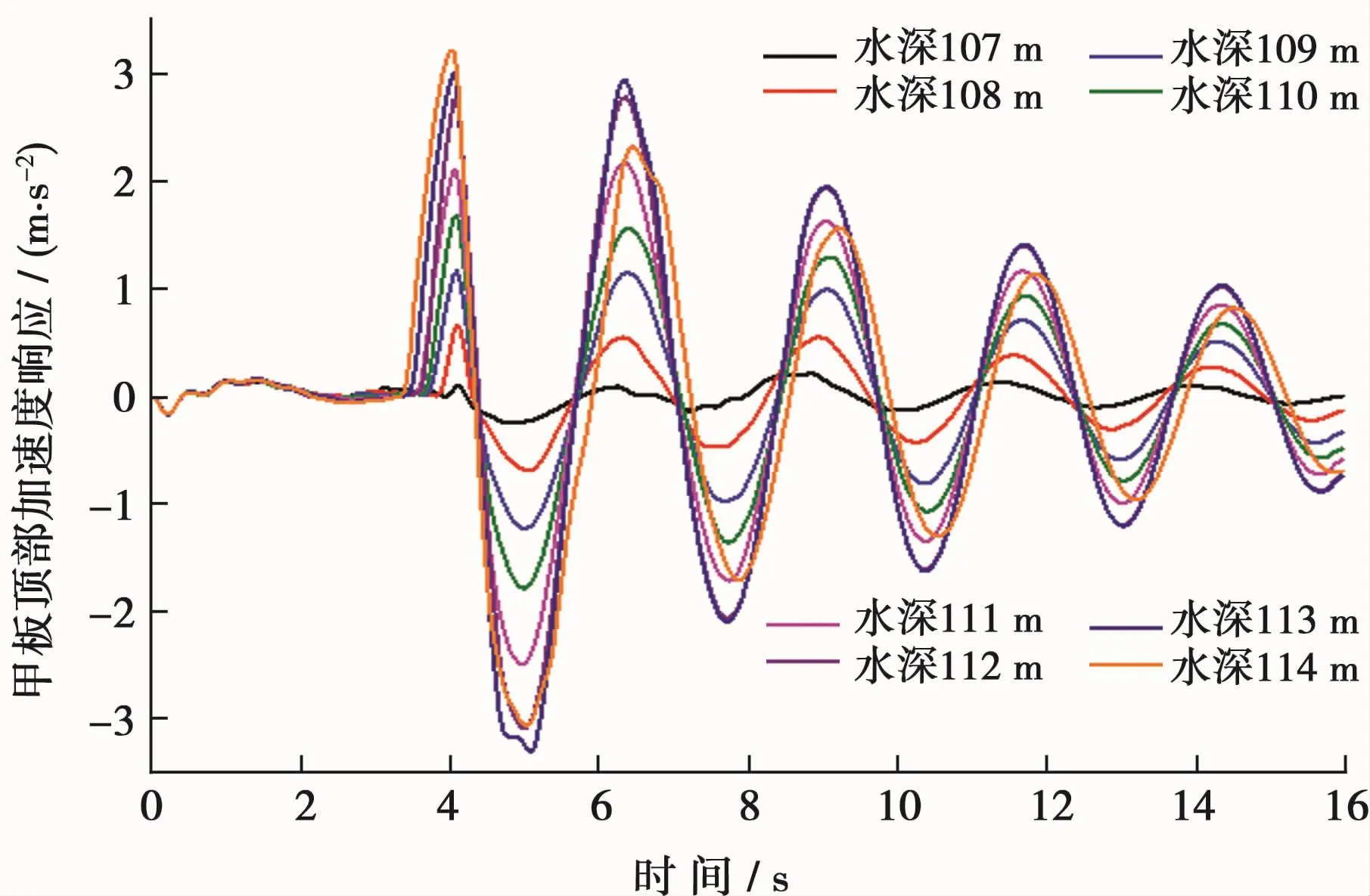
图8 不同工况下某导管架平台甲板顶部加速度响应

2.4 2种分析结果的对比

将以上2种方法得到的该导管架顶点位移列入表2,其中ueq为Fmax作用下平台静力弹塑性位移,由平台极限承载曲线插值得到。表2中亦列出了平台在Fmax作用下的线弹性位移usta,以作为参照。

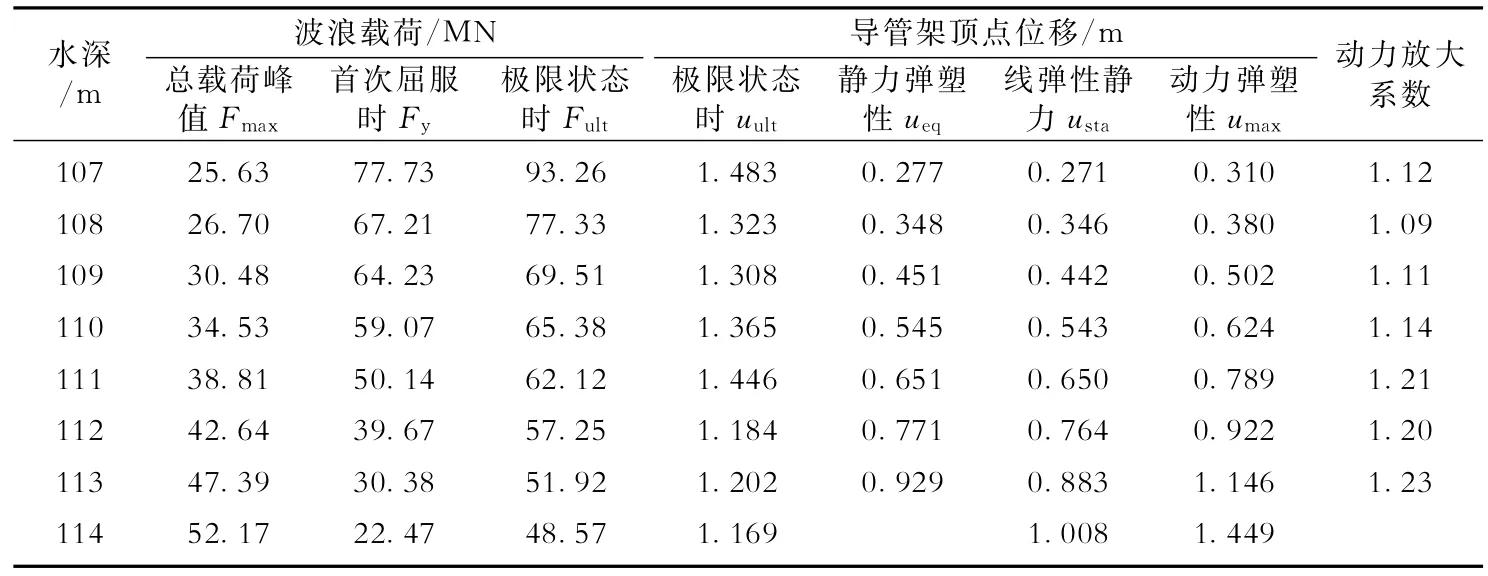
表2 不同工况下某导管架平台静力推覆分析和动力弹塑性分析计算结果对比

由表2可知,水深为107～111 m时,平台总载荷峰值Fmax均小于Fy,即平台仍处于弹性响应阶段,此时结构几何非线性影响较小,因而静力弹塑性和线弹性计算结果相差无几(相差仅为0.15%～2.2%);水深为112 m时,Fmax略大于Fy,但静力弹塑性和线弹性分析结果仍基本相同,说明轻微的塑性变形对结构的非线性性能影响并不大;水深为113 m时,Fmax接近平台极限承载能力Fult,平台塑性增强,静力弹塑性相比线弹性结果大5.2%。

对比静力弹塑性和动力弹塑性结果可知,该平台在所有工况均存在一定程度的动力放大效应,幅值增量为9%～25%。由表2中数据可知,弹性阶段平台动力放大系数相对较小,而接近或进入塑性阶段时平台动力放大系数明显增大(水深为111～113 m);水深为114 m时,Fmax已超过平台极限承载能力Fult,因而无法知晓平台动力放大系数值,若以线弹性分析结果为参照,则其响应幅值增大44%。综上分析可知,该平台塑性变形使得其动态放大效应更加显著,对平台在超强台风环境下进行评估时应考虑其动力放大效应。

此外,水深114 m时Fmax大于Fult,基于静力推覆理论认为平台此时已发生倒塌破坏,然而若以平台位移为评判指标,并认为此时的变形仍处于可接受范围时(目前尚无平台结构倒塌位移极限判据),则平台可抵御更大的外载荷。换句话而言,若采用极限承载能力Fult和极限位移双重指标作为平台倒塌的判据,则能够更好地反映平台结构的真实抗力水平。

以水深113 m工况为例,进一步分析2种方法得到的失效模式(其余工况结果类似,在此不再赘述),如图9所示。由图9可知,2种方法得到的平台塑性应变仅数值不同,其分布基本相同,说明2种方法均可以有效地揭示平台结构的倒塌机制。

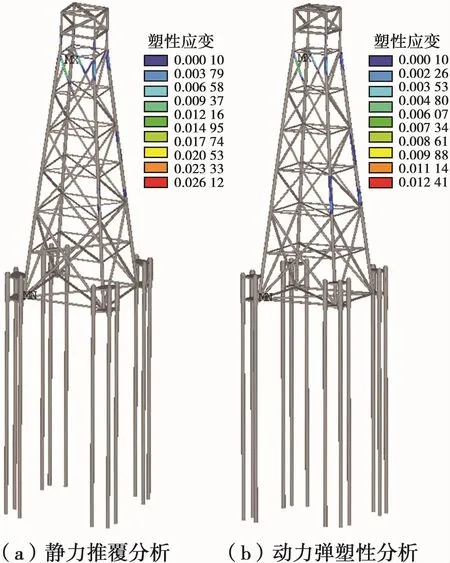
图9 静力推覆分析与动力弹塑性分析得到的某导管架平台塑性应变分布图(水深113 m)

3 结论

1)静力推覆分析能够有效计算导管架平台结构的极限承载能力,识别不同环境载荷下平台的失效模式;而动力弹塑性分析则能够有效评估导管架平台的位移与加速度响应,有利于精确确定平台结构的位移极限。因此,综合运用这2种方法可以对导管架平台抗力和刚度进行全面而真实的评估。

2)导管架平台甲板上浪载荷导致平台极限承载能力降低,对平台整体抗力影响较大,平台设计时应确保甲板气隙具有足够的安全裕量;上浪达到一定高度时,平台失效模式发生改变,导管架与上部组块连接单元发生塑性变形,当塑性变形扩大形成塑性铰时将导致平台上部组块侧翻倒塌。

3)导管架平台位移响应在整个波浪周期内均随上浪载荷的增加而增大,而加速度响应有可能因过大的塑性变形而减小(最大峰值除外);弹性与塑性阶段平台均存在不同程度的动力放大效应,且当波浪载荷极值接近或超过平台极限承载能力时动力放大效应更加显著。因此,对深水导管架平台进行偶然灾害条件下的安全评估时,应考虑其动力放大效应的影响。

[1] Minerals Management Service.Assessment of fixed offshore platform performance in Andrew,Lili and Ivan[R].2006.

[2] Minerals Management Service.Assessment of fixed offshore platform performance in Katrina and Rita[R].2007.

[3] PUSKAR F J,SPONG R E,KU A,et al.Assessment of fixed offshore platform performance in Hurricane Ivan[C].Proceedings of the 2006 Offshore Technology Conference,2006.

[4] GEORGE Z.Wave crest heights and deck damage in hurricanes Ivan,Katrina,and Rita[C].OTC 18620,2007.

[5] GRONBENH J,STERNDORFF M J.Hydrodynamic modelling of wave-in-deck forces on offshore platform decks[C].OTC 13189,2001.

[6] MURRAY J J,KAPLAN P,YU W C.Experimental and analytical studies of wave impact forces on ekofisk platform structures[C].OTC 7782,2006.

[7] CHEN H C.Time-domain simulation of nonlinear wave impact loads on fixed offshore platform and decks[J].The International Society of Offshore and Polar Engineers,2010.

[8] RAAIJ K.Dynamic behaviour of jackets exposed to wave-indeck forces[D].Norway:University of Stavanger,2005.

[9] GOLAFSHANI A A,BAGHERI V,EBRAHIMIAN H,et al. Incremental wave analysis and its application to performancebased assessment of jacket platforms[J].Journal of Constructional Steel Research,2011,67(3):1649-1657.

[10] 竺艳蓉.海洋工程波浪力学[M].天津:天津大学出版社, 1991:42-45.

[11] RAAIJ K,GUDMESTAD O T.Wave-in-deck loading on fixed steel jackets decks[J].Marine Structures,2007,20(3):164-184.

[12] API RP-2A WSD.Recommended practice for planning,design and constructing fixed offshore platforms-working stress design[S].API recommended practice 2AWSD 21st ed,2007.

[13] 董胜,石湘.海洋工程数值计算方法[M].青岛:中国海洋大学出版社,2007:237-239.

[14] MOAN T.Development of accidental collapse limit state criteria for offshore structures[J].Structural Safety,2009,31: 124-135.

[15] CHEVRON Co..Ultimate limit strength(ULS)of fixed offshore Platforms[R].2007.

[16] XU S,WANG Z J.A 3D immersed interface method for fluidsolid interaction[J].Computer Methods in Applied Methanics and Engineering,2008(197):2068-2086.

[17] 唐友刚,沈国光,刘利琴.海洋工程结构动力学[M].天津:天津大学出版社,2008:155-156.

[18] NORSOK S-002.Working environment[S].4th edition.2004.

Structure elastic-plastic analysis for jacket platform under super-typhoon

Zhu Benrui Chen Guoming Liu Hongbing Lin Hong Huang Chao Zhang Kun
(Centre of Offshore Engineering and Safety Technology, China University of Petroleum,Shandong,266580)

In view of the green water load caused by super-typhoon on jacket platform,the calculation method and procedure are established based on the trilinear time history of green water load and by using the API model and Stokes 5 th wave theory. Structure ultimate bearing capacity(UBC)and failure modes(FM)were investigated for different heights of green water by Pushover method.Further,dynamic performances of the platform under different heights of green water were studied by dynamic elastic-plastic analysis.Results show that the green water load reduces the UBC of the platform;the main FM changes from Pile foundation failure to topside rollover collapse when the height of green water reaches a certain level;dynamic amplification factor(DAF)was found of the platform both in elastic and plastic stages,and the dynamic effects was more pronounced in plastic stage.The studies of this paper provide valuable reference in the aspect of safety assessment and optimization design of deep water jacket platforms.

super-typhoon;jacket platform;green water load;pushover analysis;dynamic elasticplastic analysis;DAF;failure mode

2014-02-15改回日期:2014-06-10

(编辑:叶秋敏)

*国家自然科学基金项目(编号:51079159,51209218)、中央高校基本科研业务费专项资金资助项目(编号:13CX06079A)部分研究成果。

朱本瑞,男,现为中国石油大学(华东)博士研究生,主要从事海洋石油装备强度与可靠性方面的研究工作。地址:山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)海洋油气装备与安全技术研究中心(邮编:266580)。E-mail:zhubenrui@163.com。