预应力混凝土连续梁钢束配置分析

王海铁

（上海市政工程设计研究总院（集团）有限公司，上海市 200092）

1 概述

随着软件应用的越来越成熟、以及桥梁结构的大规模的建设，新的桥梁设计师对结构本身的细部受力及相应的关系越来越模糊，对常规桥梁跨径组合来说，都能利用基本的力学概念及以往工程经验来达到完成设计目的，但对配跨较为特殊的情况则常常出现配束不合理现象，配束指标高但对桥梁的应力贡献却很小甚至是负作用，常常在调束过程中出现死循环，但却找不到问题的实质，从而浪费了大量的时间，却达不到优化设计的目的。因此，有必要对常规预应力混凝土连续梁的受力进行重新梳理，结合软件快速有效地完成设计。实际工程中，配束出现多配、少配、错配等问题的根本原因是未完全掌握次弯矩的规律，甚至未理解次弯矩。

2 理论分析

对于预应力混凝土连续梁，当施加预应力后，就产生主弯矩M，同时，梁产生弯曲变位，使其自身有离开支承之势，但是由于不是简支，支承处结构可能发生的变形就要改变或受到阻碍、约束，从而引起附加反力，称之为次反力，由次反力引起的弯矩称为次弯矩，这种预加应力时变形受约束所产生的次弯矩并非在数值上是次要的，而是结构的应力和强度计算中很重要的一部分。预应力引起的综合弯矩=主弯矩M1+次弯矩M2。

通过预应力连续梁的软件计算分析可知其预应力产生的次反力（次反力的理论计算可采用荷载平衡法），进而可知，在各个竖向约束下中支承处的主梁截面的预应力次弯矩。

预应力混凝土连续梁由于预应力引起的应力效应由三部分组成，永存预应力张拉力F，预应力相对截面形心产生的主弯矩M1，由于超静定作用产生的次弯矩M2。

预应力偏心距e，三跨连续梁边跨长为L，截面惯性矩I，截面上下缘相对截面形心的距离y，则上下缘的压应力计算公式为：

对于轴压力、主弯矩这两项，只要知道截面及钢束相对形心的位置就可知道相应的应力。不确定的因数为次弯矩，以25 m+32 m+25 m预应力混凝土连续梁为例，分析各种不同配束对连续梁的作用，及规律性认识。

3 实例分析

示例连续梁跨径布置为25 m+32 m+25 m，桥宽8.5 m，梁高1.7 m，单箱单室，其钢束布置如下：腹板束F1、F2、F3为2-12φs15.2，顶板束T1、T1′、T2、T2′为4-7φs15.2，底板束D1、D2、D3、D4、D5为2-7φs15.2，具体配束见图1。

图1 配束示意图（单位：cm）

预应力混凝土连续梁最主要的荷载有：收缩徐变、整体温度、温度梯度、支座沉降、恒载、汽车人群荷载等。对于给定跨径的预应力混凝土梁桥设计，通常均为正常使用极限状态控制，而应力控制点主要部位有支点上缘、支点下缘、跨中上缘、跨中下缘。而这些点的应力控制主要通过腹板束、顶底板束来实现，不同的配束方式对各支点的应力控制有很大差别。

腹板配束相对定型，一般通长布置，遵循跨中区域布置在下缘，支点区域布置在上缘。需要注意的是在支点附近腹板束的起弯位置及弯起斜率对抗剪及支点下缘应力有一定的影响，配束须注意，下面主要对顶板束、底板束进行分析。

（1）顶板束

通过建模计算，可知T1、T1’、T2、T2’钢束在支座处产生的次反力，具体见表1。

表1 顶板束在支座处产生的次反力

根据建模计算的各钢束作用下的应力弯矩情况见表2。

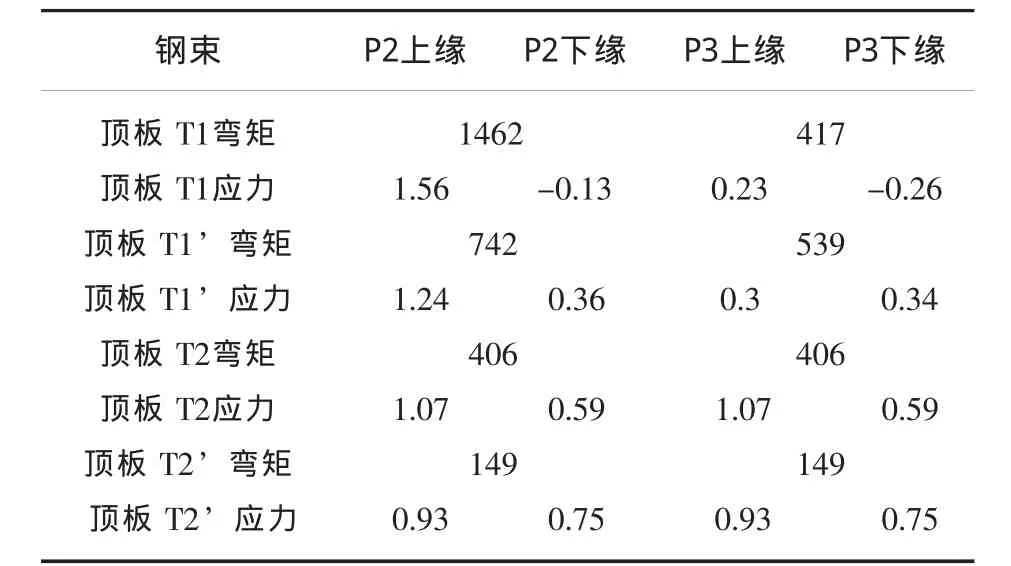
表2 顶板束作用下的应力弯矩情况

从上面的计算结果不难看出，对于支点P2，上缘正应力T1＞T1’、T2＞T2’，下缘T1＜T1’、T2＜T2’；对支点P3，上缘正应力T1＜T1’、T2＞T2’，下缘T1＞T1’、T2＜T2’；T1、T1’钢束对P2、P3钢束均为上缘均为正效应，对下缘为负效应，而T3钢束对上下缘均为正作用。

由此可以得出以下结论：对于三跨连续梁，过单支点、双支点的顶板钢束，钢束长度越短，对支点上缘正应力越有效，钢束越长，对支点上缘正应力效果越差。这从理论公式中就可以看出来，对于给定跨径的连续梁，对于顶板钢束，公式中除次反力F次为变值外，余均为定值，当钢束长度加长，则次反力增大，F次·L增大，由于F次为负值，截面上缘总应力减小，下缘总应力增大，与模型计算结果吻合。

（2）底板束

底板束其最直接的作用是满足跨中区域处的正弯矩的受力要求，正常设计较容易满足，主要研究底板束对支点区域处的应力作用。通过建模计算，可知D1、D2、D3钢束在支座处产生的次反力，具体见表3。

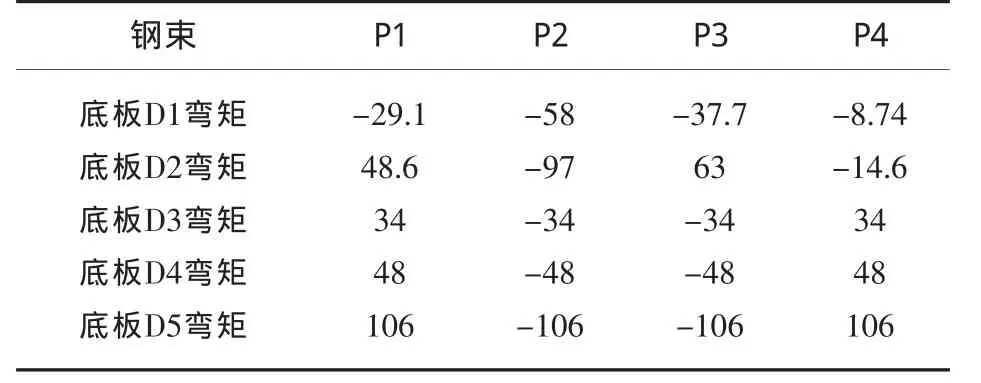
表3 底板束在支座处产生的次反力

根据建模计算的各钢束作用下的应力弯矩情况见表4。

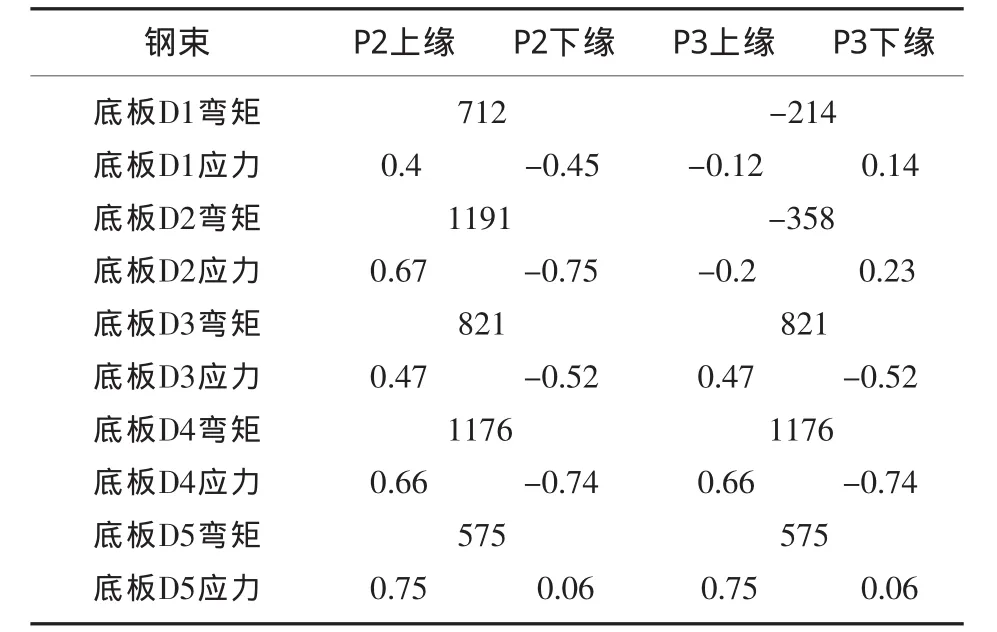
表4 底板束作用下的应力弯矩情况

从上面的计算结果不难看出，对于D1、D2钢束，P2支点处上缘正应力D1＜D2，下缘正应力D1＞D2；而P3支点处，上缘正应力D1＞D2，下缘D1＜D2。D1、D2钢束为作用在第一跨，钢束对P2支点上缘均为正效应，下缘为负效应，P2、P3处受力相反的关系可利用连续梁作用影响线关系得到解释。由此可以得出以下结论：对于支点下缘应力控制较紧张的情况下，底板应尽量布置短束，锚固点应远离支点。

对于D3、D4钢束，其作用规律同D1、D2钢束，因此对于支点下缘应力控制较紧张的情况下，也应尽量布置短束，锚固点远离支点。

对于D5钢束，如果不仔细分析，常认为对支点下缘有利，对于本示例，钢束对支点下缘的有效作用几乎为零，根据理论公式，其决定作用的为F次·L，对于给定跨径L，只跟钢束的长短有关，而对于底板通常束，调整余地很小，因此基本为定值，在计算时须先判断下，再做判断。

4 结论

本文对预应力作用的基本理论知识进行了介绍，并结合有限元软件，对三跨预应力混凝土连续梁的主要配束方式进行了规律性的认识。实际工程中会遇到各种各样的预应力混凝土连续梁，因此除了需了解常规配束规律外，还要利用理论知识及有效的分析方法对各种不同预应力混凝土连续梁进行快束而合理的设计。

[1]范立础.预应力混凝土连续梁桥[M].北京：人民交通出版社，1997.

[2]林同炎.预应力混凝土结构设计[M].北京：中国铁道出版社，1983.