锯齿型三角石墨烯电子结构的量子尺寸效应*

周晓飞, 童国平

(浙江师范大学 凝聚态物理研究所,浙江 金华 321004)

0 引 言

长期以来，人们一直以为二维形式的碳材料是不存在的[1-3]，直到2004年，英国曼彻斯顿大学Novoselov等[4]用机械剥离的方法成功制备了石墨烯[5-6].石墨烯因具有许多奇特的物理性质而引起人们的广泛关注，如半整数量子霍尔效应[7-8]、Klein 遂穿[9]、量子尺寸效应等[10-12].一定尺寸的石墨烯纳米片是在二维石墨烯的基础上经过一定方法剪裁得到的，在低维纳米结构中，不同的边缘结构、大小和形状会对石墨烯的费米面处的电子性质产生一定的影响.从边缘结构上可分为扶手椅型和锯齿型2类，整体形状结构有正三角形、方形、正六边形、圆形.Akola等[13]使用密度泛函方法和紧束缚方法对一定尺寸锯齿型和扶手椅型三角状石墨烯的电子结构进行了计算;Zarenia等[14]使用紧束缚方法和狄拉克方法研究了正三角和六角状石墨烯片的电子性质;Ezawa[11]使用数值的方法研究了不同大小和形状的锯齿型和扶手椅型石墨烯纳米结构的电子性质，对于方形带状的零维纳米结构，当长度无限增大时，开始出现平能带和简并的零能态，而扶手椅型由于大小的不同存在奇偶效应，能隙大小随横向原子个数的增加而减小，而且只有在锯齿型三角状结构中存在零能态;Potasz等[15]构造了零能态的波函数，证明了零能态的简并度源于2种原子数目的差值；同年，Rozhkov等[16]构造了局域在三角结构上的波函数，研究了扶手椅型三角状石墨烯的电子性质.尽管人们已经做了大量的工作，但是对量子尺寸效应及能带结构中电子态的研究却很少.

笔者采用紧束缚方法计算锯齿型三角形状石墨烯纳米片的电子结构，着重研究了量子尺寸效应.随着边界原子个数N的增加，能隙(零能态和第一激发态之间的差值)逐渐减小，能带的宽度逐渐变宽.N较小的时候，能够取得一些分散的能带；当N足够大时，能带曲线已经出现在整个空间范围内.

1 理论方法和模型

考虑一定大小正三角形锯齿型石墨烯片，如图1所示.

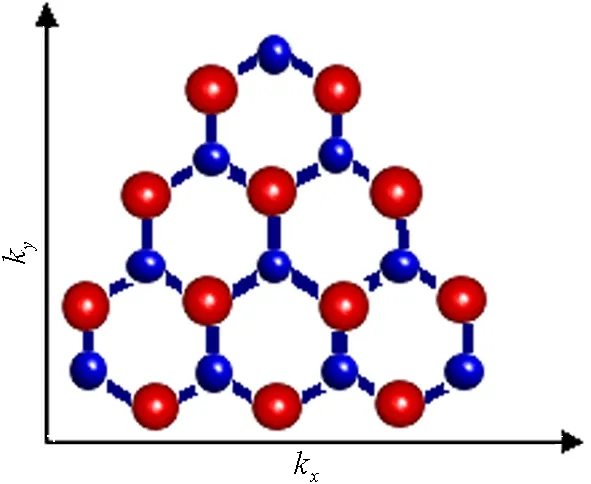
大球表示A原子；小球表示B原子图1 三角形锯齿型石墨烯片

采用紧束缚方法[17]，在考虑最近邻电子跳跃的情况下计算石墨烯纳米片的电子结构.石墨烯纳米片的哈密顿量为

(1)

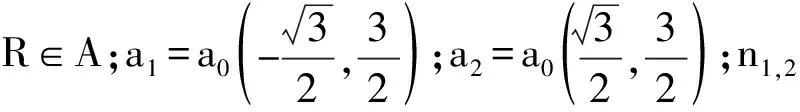
(2)

相应的晶格内部原子薛定谔方程可以写为:

边界原子上的薛定谔方程可以写为

(5)

(6)

(7)

(8)

可以计算出一定大小尺寸的石墨烯纳米片的态密度，扩展因子Γ=0.05.

2 结果与讨论

笔者计算了边界原子个数为N=5,12,50(每边的长度为L=1.5,3.2，12.5nm)的锯齿型正三角形状石墨烯纳米片的态密度和N=3时kx方向的色散关系,具体见图2.

图2 边界原子个数分别为5,12,50的态密度曲线

从图2的态密度曲线中可以看出，各种尺寸石墨烯片都显示金属性.图2中，(a),(b),(c)分别表示N=5,12,50的态密度曲线，态密度曲线在E=0处有一个尖峰.随着N的增加,尖峰的高度逐渐增加，这源于N-1重简并的零能边缘态.随着N数目的增大，石墨烯纳米片的能带宽度变窄，能隙逐渐减小;当N达到一定数值以后，能隙的大小与1/N成比例，而且当边界原子数目达到N=50时，态密度曲线与无限大石墨烯片整体相似.

三角状锯齿型石墨烯片主要存在2种电子态，分别是边缘态与驻波态，驻波态波函数是正弦函数形式，边缘态波函数是双曲正弦形式，其能带结构由边缘态能带和驻波态能带组成,具体见图3.图3中,(a)是kx,ky均取连续值时候kx方向能带的变化;(b)是ky=1时能带在kx方向的变化曲线.由于费米面附近的能带中存在边缘态和驻波态，笔者着重研究了费米片处的几条能带(除简并的零能态组成的能带)，结果发现:随着|ky|的增加，驻波态能带的宽度逐渐变窄，即在|ky|=0时，驻波态能带的宽度最大.但能量本征值却随着ky的改变而改变，当ky>0时，随着|ky|的增加，驻波态能量的变化范围越来越小，驻波态数目在中心带中比例下降；当ky<0时，随着|ky|的增加，驻波态能量的变化范围越来越大，驻波态数目在中心能带中的比例呈现增加的变化趋势.随着N的增加，能带曲线的宽度变窄，所得的能量值的范围变大，但驻波态的宽度并无明显变化.对于边缘态而言，当ky=0时，边缘态能带的宽度最窄，但是无论ky如何变化，边缘态能带的宽度始终保持在一定范围内.值得注意的是，随着ky的增加，小能量的边缘态越来越多，这就导致边缘态能带中出现了一段较陡峭的能带.随着N的增加，即锯齿型三角石墨烯片逐渐变大，边缘态中接近于0的能态越来越多，边缘态的宽度也变大，但较陡峭的能带逐渐消失.当N很大时，中心能带由两端的驻波态能带和中间的平能带组成，与二维石墨烯纳米带的中间能带的组成已经一致.

(a)kx,ky连续变化时能带变化 (b)ky固定时能带在kx方向的变化

3 结 论

小尺寸的锯齿型石墨烯片具有特殊的电子结构，并且具有简并的零能态，使得各种大小的石墨烯片呈现金属性，而且零能态的简并度可以通过改变边界的长度来调控，这对于耦合纳米器件的制造有很大的意义，而且当三角状石墨烯片的尺寸增大到足够大时，电子性质与二维石墨烯相类似.

参考文献：

[1]Peierls R E.Quelques proprietes typiques des corpses solides[J].Ann I H Poincare,1935,5(3):177-222.

[2] Landau L D.Zur theorie der phasenumwandlungen II phys[J].Z Sowjetunion,1937,11:26-35.

[3]Landau L D,Lifshitz E M.Statistical physics[M].Pergamon:Oxford,1980.

[4]Novoselov K S,Geim A K,Morozov S V,et al.Electric field effect in atomically thin carbon films[J].Science,2004,306(5696):666-668.

[5]Sadowski M L,Martinez G,Potemski M.Landau level spectroscopy of ultrathin graphite layers[J].Phys Rev Lett,2006,97(26):266450.

[6]Ferrari A C,Meyer J C,Scardaci V,et al.Raman spectrum of graphene and graphene layers[J].Phys Rev Lett,2006,97(18):187401.

[7]Saito R,Gdresselhaus G,Gdresselhaus M S.Physical properties of carbon nanotubes[M].London:Imperial College Press,2003:1-33.

[8]Zhang Yuanbo,Tan Yanwen,Stormer H L,et al.Experimental observation of the quantum hall effect and berry′s phase in graphene[J].Nature,2005,438(7065):201-204.

[9]Katsnelson M I,Novoselov K S,Geim A K.Chiral tunneling and the klein paradox in graphene[J].Nature Physics,2006,2(9):620-625.

[10]Nakada K,Fujita M,Dresselhaus G,et al.Edge state in graphene ribbons:nanometer size effect and edge shape dependence[J].Phys Rev B,1996,54(24):17954.

[11]Ezawa M.Metallic graphene nanodisks:Electronic and magnetic properties[J].Phys Rev B,2007,76(24):245415.

[12] Dasgupta A,Bera S,Evers F,et al.Quantum size effects in the atomistic structure of armchair nanoribbons[J].Phys Rev B,2012,85(12):125433.

[13]Akola J,Heiskanen H,Manninen M.Edge-dependent selection rules in magic triangular graphene flakes[J].Phys Rev B,2008,77(19):193410.

[14]Zarenia M,Chaves A,Farias G,et al.Energy levels of triangular and hexagonal graphene quantum dots:A comparative study between the tight-binding and Dirac equation approach[J].Phys Rev B,2011,84(24):245403.

[15]Potasz P,Güclü A D,Hawrylak P.Zero-energy states in triangular and trapezoidal graphene structures[J].Phys Rev B,2010,81(3):033403.

[16]Rozhkov A V,Nori F.Exact wave functions for an electron on a graphene triangular quantum dot[J].Phys Rev B,2010,81(15):155401.

[17]Reich S,Maultzsch J,Thomsen C.Tight-binding description of graphene[J].Phys Rev B,2002,66(3):035412.