基于边界扩张的点对点布线新算法

廖海涛，史 峥，张 腾

(浙江大学超大规模集成电路设计研究所，杭州 310027)

基于边界扩张的点对点布线新算法

廖海涛，史 峥，张 腾

(浙江大学超大规模集成电路设计研究所，杭州 310027)

在超大规模集成电路设计中，全局布线是非常重要的步骤。工业界普遍采用经典的迷宫算法及其改进算法解决全局布线问题。随着工艺节点的减小，传统迷宫算法复杂度高的缺点越来越明显。针对传统迷宫算法的复杂度会随着布线规模的扩大而迅速增加的问题，借助于边界扩张的概念，提出一种新的点对点布线路径的搜索算法。摒弃了迷宫算法低效率的逐个节点扩张的思想，通过自由节点的定义对节点边界进行迅速扩张并不断地找到新的自由节点，直到找出路径或确定无解时结束。将该算法与经典的布线算法进行理论和实验比较，结果表明在大多数情况下该算法使用经典算法7%～14%的运行时间即可完成路径搜索。

超大规模集成电路；全局布线；迷宫算法；点对点布线；边界扩张；自由节点

1 概述

全局布线是物理设计中布局之后的重要步骤，布局确定了模块在芯片上的位置以及模块上各引脚的分布，并通过网表提供了各引脚间的互连信息。布线过程就是实现各模块间的连接。全局布线作为布线过程的第一步，目的就是把每条线网的各个部分合理地分配到各个布线通道中去，为之后的详细布线提供初始布线走向，这一阶段布线结构的好坏决定芯片的整体性能。

现有超大规模集成(Very Large Scale Inte grated, VLSI)电路计算机辅助设计系统大多是基于统一标准的网格模型。这种模型的布线算法大致分为2类：迷宫算法和线搜索算法[1]。迷宫算法常见的是穷举回溯的深度优先搜索方法和层层推进式的广度优先搜索方法。文献[2]算法作为最原始的迷宫算法，采用的就是广度优先搜索方法。这类算法的优点是实现简单，并且总能够保证找到最短路径，而缺点在于其时间和空间复杂度都比较高[3]。为了降低复杂度，出现了许多改进版本[4-6]，其中，A*[6]算法是目前工业界普遍使用的启发式搜索算法，它通过选择合适的启发函数，使其寻找最优路径的搜索范围比原始算法更小。国内关于迷宫算法的研究[7-9]主要是针对原始迷宫算法加入启发条件来改进搜索效率。这些改进算法并没有改变传统迷宫算法逐个节点的搜索方式，只是通过加入启发条件来缩小搜索范围，并没有从根本上改变迷宫算法的复杂度。

为摆脱逐个节点搜索的限制，人们提出了线搜索算法。基本思想是构造一个比原始网格更加稀疏的子图，通过在子图中寻找最短路径得到原格点中的路径。较早的线搜索算法[10]被提出后，又有学者引入了新的连接图来代替原始网格[11-12]，甚至有学者引入了一种新的迷宫驱动型线搜索算法[13]。这些算法在理论上都比原始的迷宫算法复杂度要低，然而实际应用中由于集成电路规模巨大，构造这种子图的时间代价往往非常大，因此这类算法并没有被普遍采用，而只是在设计初期障碍数目较少时使用；此外一些线搜索算法甚至还无法保证搜索到布线路径，即使这条路径的确是存在的。国内学者受到线搜索法的启发也相应提出用于VLSI二维布线的新方法[14]，也有学者将线搜索法与迷宫算法结合并将其应用于三维电气网络的自动布线中[15]。

本文提出一种新的算法，与线搜索算法类似，没有使用逐个节点扩散的搜索方式，而是给出了一种新的搜索方式。

2 基本概念和定义

2.1 网格模型

一般来讲，全局布线问题可以建模为一个网格图G=(V, E)，如图1所示，图中位于每个网格中心的点(用黑色圆点表示)V( vi, vj)={(vi, vj)|0≤i＜m∩0≤j＜n}就对应代表了这个网格，而两点之间的虚线则对应代表了2个网格之间所夹的边缘。

图1 划分成m×n的版图和与之对应的网格模型

2.2 自由节点的边界

定义1(自由节点的边和边界) 如图2所示，假设点A为自由节点，以A为原点向4个方向作垂线，遇到第1个障碍物时到达的节点为垂足，则与每条垂线垂直且经过对应垂足点的连续障碍节点构成的线段称为节点在该方向上的一条边；以这4条边确定的矩形区域称为自由节点A的边界。图2中的加粗实线表示自由节点的边界，加粗虚线表示自由节点到相应方向边上的垂线。

定义2(节点相对于边界的内与外) 是指该节点与另外某节点边界的相对位置。如图2所示，P1位于A点的边界内部，而P2与P3位于A点的边界外部。

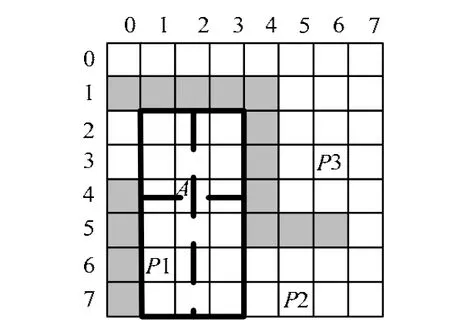
图2 自由节点A的边界示意图

2.3 闭合边、半开放边与开放边

定义3(闭合边、半开放边与开放边) 本文提到的3种边都是相对于某个节点而言的，同样提到某条边是闭合或者开放时，也是相对于某个确定节点而言的。图3中点A的右侧边与点B的左侧边均为边CD，但是C点左侧有障碍点存在，形成一个向左下方向的直角(如图中C点区域内的拐角线标注)这2条以点C为端点和射线构成的区域把点A包含在内，因此定义边CD的上部端点C相对于点A来说是闭合的，但是相对于点B是开放的；同理边CD的下部端点D相对于点A是开放的，但相对于点B却是闭合的。然而无论是对点A还是点B，都只有一个开放端点和一个闭合端点，这种一个端点开放而另一个端点闭合的情况称此边为半开放边。节点B的右边界FG的2个端点旁边都没有其他的障碍点与之构成能够包含节点B的直角，它们相对于节点B都是开放的。这种2个端点相对于该节点都开放的边称作开放边。同样可以分析，节点A的上边界EC 的2个端点相对于节点A都是闭合的。这种2个端点都闭合的边称作闭合边。图3中的加粗实线表示自由节点边界上的拐角，加粗虚线表示自由节点到相应方向边上的垂线。

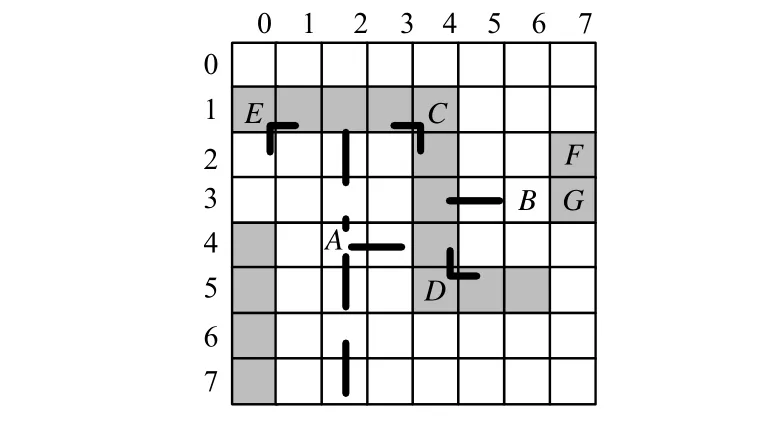
图3 3种不同类型的边

性质1整个网格模型的4条边框中的每一条对任意节点都是闭合的。这是由任何节点(包括空白节点和障碍节点)都必须在网格内部决定的。

定义4(边的有效长度) 是指一条边的非闭合部分长度。

定义5(开放端点) 开放边与半开放边中非闭合一端的端点称为开放端点。一条开放边有2个开放端点，而半开放边只有1个开放端点。

定义6(完全闭合) 是指一个自由节点的4条边界均为闭合边。

2.4 自由节点

定义7(自由节点) 是指可以逃离边界的点。自由节点必须同时满足以下2点：(1)必须是在前一级自由节点的边界外部且与边界邻接；(2)必须是前一级自由节点的开放边端点的邻近点。一个实例如图4所示，节点P1和P2即为新的自由节点。图中的加粗实线表示自由节点的边界，加粗虚线表示自由节点2个自由节点间的连接线。

图4 节点P1与P2为新的自由节点实例

性质2自由节点与它对应的上一级自由节点之间可以通过一条固定路径的Z型路径或者L型路径相连。

证明：以图4中的节点P2和它的上一级节点A来证明。设A点坐标为(x1,y1)，P2点坐标为(x2,y2)。由于P2点处于A点的边界邻接位置，则可以找到这样一点N(x3,y3)，使得N与P2可以直接以直线相连。

下面证明点N与点A可以简单连接(反证法)：由于点N处于边P1P2的端点处，假设点N与点A之间不能简单连接，则必然有一个障碍存在于A到边P1P2之间或者A到该边的垂足与点N之间，若该障碍存在于A到边P1P2之间，则A点下边界将会改变而不再是P1P2，与已知条件冲突；若该障碍存在于A到该边的垂足与点N之间，则A点下边界的右端点将不再是开放边，也与已知条件冲突。故假设不成立，即点N与点A可以简单连接。同样对于点A处于下边界的位置时，点N与点A可以直接进行简单连接。

由以上2点可知，节点P2和它的上一级节点A之间可以通过一条固定路径的Z型路径或者L型路径相连，证毕。

定义8(简单连接) 如果两点之间可以通过直线或L型路径相连，即2个节点具有相同的横坐标或纵坐标且与该节点之间没有障碍，或者可以找到一个新的节点，使得该节点分别与2个原来的节点有相同的横坐标和纵坐标且与该节点之间都没有障碍。定义两点之间的这种连接为简单连接。如图5中的2幅图，节点A与节点B之间的连接都属于简单连接。

图5 2种简单连接

3 算法的基本思想、实现与分析

3.1 算法的基本思想

对于两点间布线路径查找问题，本文算法的基本指导思想是从源节点与目标节点开始，通过节点的边界找到新的下一级节点，再通过下一级节点的边界扩张找到新的子节点，直到从源节点扩散出的子节点与从目标节点扩散出的子节点可以通过简单连接实现互连为止。

可以将本文算法思想抽象理解为树的结构，如图6所示，源节点S与目标节点T分别是2棵树的根节点，让这2棵树不断向下生长直到2棵树的叶节点有相交部分为止。图中所示为通过节点Sm与节点Tn的连接找到了布线路径。

图6 算法的抽象树示意图

每当一个父亲节点产生新的子节点时，就表明通过自由节点的边界扩张找到了新的自由节点。树的高度相当于节点扩散的效率，高度越大说明迷宫地形越复杂。在每一级父亲节点产生子节点之前都会对2棵树进行比较，取节点较少的树进行生长以保证查找效率。

3.2 算法的实现

给定网格G=(V, E)及源节点S=(Si, Sj)和目的节点T=(Ti,Tj)，增加集合FREEPOINTSA与FREEPOINTB分别存放起点和终点引出的最新的自由节点；增加标志位DETOUR表示是否存在迂回节点；用四点集合CLOSED表示发生完全闭合时自由节点的边界范围。

算法1基于边界扩张的点对点布线算法

步骤1初始化，令FREEPOINTSA={S}, FREEPOINTSB= {T}，迂回标志位DETOUR=0，集合CLOSED={0,0,0,0}，并以FREEPOINTSA为起始集合进入步骤2。

步骤2从传入此步骤的集合(以下称为起始集合，而另一个集合则称作目标集合)开始，对集合中的每个自由节点进行边界扩张，获取新的自由节点，直到算法终止。

(1)判断起始集合与目标集合中是否有节点可以通过直线或者L型路径进行简单连接，若有，则转步骤3。

(2)从起始集合开始，利用算法2检测每个节点的4个边界，获取4条边的有效长度，对开放边和半开放边，记下开放端点的标记位，保证每个开放边只有一个自由节点。

(3)判断目标集合中是否有自由节点存在于起始集合自由节点的边界内部。若不存在，以起始集合为输入转步骤(4)；若存在，以目标集合为输入转步骤(4)。

(4)判断传入的起始集合中每个自由节点的边界是否为完全闭合，若是完全闭合，判断闭合原因，如果是障碍引起的完全闭合，则转移节点到可以使边界改变的边，删掉原节点，增加符合条件的新节点；若是由前一级节点的边界引起的完全闭合，则利用算法2重新计算该节点的边界。

(5)记下此时的边界4点值并与CLOSED中的4个值相比较，若相同，说明发生循环，此节点无法通过新的自由节点逃离边界。若起始集合每个自由节点均无法逃离，则无路可走，算法结束；否则将DETOUR置1，并以目标集合为输入转步骤(1)。

(6)获取起始集合中新的自由节点，更新起始集合，并让集合中的每个自由节点通过指针指向能够得到该节点的前一级自由节点。例如，若自由节点P1通过边界扩张得到了新的自由节点P2，则通过指针让P2指向P1(即P2→P1)，目的是在后面的布线步骤中可以直接找到前一节点。

(7)判断起始集合与目标集合中自由节点的数量，从节点数目少的集合作为起始集合转到步骤(1)。

步骤3这里的输入是分别来自2个集合中的某个自由节点，进入此步说明已经找到通路，2个集合中的自由节点可以由一条直线或者L型路径相连。这一步的主要工作便是布线与迂回处理。

(1)用直线或者L型路径连接这2个自由节点。

(2)对每个集合中的自由节点，通过步骤2中的指针连接前一级自由节点，直到到达S或T为止。

(3)检测DETOUR的值，若DETOUR=1，使用算法3消除迂回路径，算法结束；若DETOUR=0，算法结束。

算法2获取自由节点的边界算法

(1)检查该自由节点是否是节点S或者节点T，若是，则转步骤(2)；若不是，则转步骤(3)。

(2)以自由节点为中心向4个方向延伸检测，遇到障碍物时停止，记下该障碍的位置，4个方向的障碍边围成的边界即为该节点的边界。

(3)以节点为中心向4个方向延伸检测，遇到障碍物或前一级节点的边界时停止，记下该障碍或边界的位置，4个方向的障碍或边围成的边界即为该节点的边界。

算法3消除迂回路径算法

对已经布线的所有非起始自由节点(即，除了点S与点T之外的自由节点)进行检查，一个正常的自由节点会有2条相互垂直的布线路径，而迂回节点则只有一条。对于每个迂回节点：

(1)将此节点移动到布线路径方向的相邻节点，并删除与原节点间的路径。

(2)对新节点进行检查是否为迂回节点，若是迂回节点，则转步骤(1)；若不是，算法结束。

消除迂回路径算法的示意图如图7所示，图中X标记的部分将被消除，P2会移动到没有迂回路径的节点。

图7 迂回路径的消除

3.3 算法的复杂度分析

由于本文算法从2个需要连线的起点开始以边界向外扩张，因此算法的复杂度与障碍物的分布和障碍物的边长有关，整个算法有2个主要耗时部分：第1部分是边界扩张和查找新的自由节点；第2部分是每次边界扩张之前进行的自由节点间是否可以由简单路径相连的判断。

先分析第1部分的复杂度：假设整个搜索路径的过程中所使用到的开放端点数为e(并不是所有的开放端点都会被使用到)，这些开放端点都是自由节点；且与每一个使用到的开放端点iP对应的边界周长为Ci，该节点边界所在的4条边在边界内部的有效长度之和为Si，该节点边界所在的4条边的实际长度之和为Li那么有Si≤Li，且整个算法过程中搜索的节点总数为：自由节点的4条边界长度与其实际长度不一定相等，方便起见取两者近似相等，有ii

L≅C，于是式(1)可得到：

在最坏的情况下，需要把所有遇到的障碍边都搜索到而且每条障碍边都会被它两侧的自由节点搜索一遍，也就是说每条障碍边都会被搜索2次。假设所遇到的障碍物边的总长度为L，于是有：

由式(2)与式(3)可以知道：T=3L，即该算法的边界扩张部分的时间复杂度为O( L)。

第2部分的复杂度主要是由2个源节点扩散出来的新的自由节点间是否可以通过简单路径相连，这里所有判断的2个节点都是确定位置的，而且简单路径的路径判断也最多只有2种情况，所需要的时间也与2个节点的位置有关。取最坏的情况来分析，假设所有自由节点都存在于整个网格G的对角上(实际当然不可能如此，但这2个节点必定位于网格G中且距离不可能比对角距离更远)，那么对于一般情况而言，必然存在一个值k∈(0,1]，使得对于所有e个自由节点进行判断花费的时间为ke( m+n)2，那么对于整个算法中所有自由节点间是否可以用简单路径相连判断的复杂度就是O( e( m+n))。

综上所述，该算法总的时间复杂度为O( L+e( m+n))，由于仅需要保存新的自由节点，算法空间复杂度为O( e)。

4 实验结果与分析

将本文算法与经典迷宫算法和A*算法应用于具体实例中，其中A*算法使用当前节点与目标节点之间的Manhattan距离作为启发条件，迷宫由随机产生障碍节点的程序随机生成。针对不同规模的迷宫，对3种算法获取布线路径所需要时间和与经典算法运行时间之比分别作统计，见表1。

表1 3种算法的实验比较

从表中数据可以看出，A*算法与本文算法都能够明显减少运行时间。在规模最小的8×8迷宫中，A*算法使用了经典算法64.7%的运行时间，本文算法则使用了41.2%；在其他5组较大规模的迷宫中，A*算法使用的时间在经典算法的36%～60%之间，而本文算法则仅仅使用了7%～14%的时间，可见本文算法要明显优于另外2种算法。在相同疏密度(即障碍与路径比)的迷宫中，随着迷宫规模的增大，经典迷宫算法需要查找的节点成倍增加，导致运行时间迅速增长；A*算法的性能略有提升，说明加入启发条件之后对于大规模迷宫查找路径确实有一定的指导作用；而本文算法的运行时间相比于迷宫规模的增长速度来看相对稳定，线性效果明显，因此，在规模较大的迷宫中运行的整体效率比规模较小的迷宫有所提高。

由第3节中得出的时间复杂度可以看出，本文算法的复杂度与障碍物的数量和分布相关。在迷宫的疏密度较低时，后续实验表明运行时间可以进一步减少到5%甚至更低，然而在迷宫的疏密度较高且障碍分布杂乱时算法的效率会随之降低，说明在迷宫的疏密度很高并且障碍分布杂乱时算法的效率会比较低。这是因为本文算法的指导思想是让拐线尽量少来快速地找到路径，障碍分布杂乱时产生的新自由节点会更多，复杂度随之增加。

5 结束语

本文提出一种新的点对点布线的算法，算法的创新点在于：(1)提出了自由节点和节点边界等新的概念，每一个自由节点的出现都以逃离与它对应的上一级自由节点的边界为目的。(2)算法通过节点边界的扩张实现自由节点的转移，从而快速地从源节点向目标节点扩散，大大提高了搜索效率。该算法的优点是既克服了传统迷宫算法基于遍历网格的高复杂度的缺点，也无需在庞大的网格中搜索障碍构造子图。通过对自由节点边界的扩张不断搜索路径，理论分析和实验结果表明，该算法可以很好地解决点对点的布线问题且复杂度较低。以后的工作可考虑加入启发条件，以降低迷宫疏密度较高的特殊情况出现时算法的复杂度。

[1] Alpert C J, Mehta D P, Sapatneka r S S. Handbook of Algorithms for Physical Design A utomation[M]. [S. l.]: Auerbach Publications, 2009.

[2] Lee C Y. A n Algorithm for Path Connection and Its Applications[J]. IRE Transactions on Electronic Computers, 1961, 10(3): 346-365.

[3] 周 智, 蒋承东. Ma nhattan空间有障碍的最短路径和3-Steiner树算法[J]. 软件学报, 2003, 14(9): 1503-1514.

[4] Akers S. A Modification of Lee’s Path Connection Algorithm[J]. IEEE Transactions on Electronic Computers, 1967, 16(2): 97- 98. [5] Soukup J. Fast Maze Router[C]//Proc. of t he 15th Design Automation Conference. Piscataway, USA: IEEE Press, 1978: 100-102.

[6] Hart P E. A Formal B asis for the H euristic Determination o f Minimum Cost Paths in Graphs[J]. IEEE T rans. on Systems Science and Cybernetics, 1968, 4(2): 100-107.

[7] 胡湘萍, 陈利军. 迷宫算法的改进与动态实现[J]. 电脑知识与技术, 2007, 2(8): 490-491.

[8] 陈传波, 胡谊东, 何 力, 等. 目标驱动的迷宫布线算法及优化[J]. 华中科技大学学报: 自然科学版, 2004, 32(1): 49-51.

[9] 权建洲, 韩明晶, 李 智. 基于改进A*算法的电子制造装备布线方法研究[J]. 中国科技论文在线, 2009, 4(8): 555-559.

[10] Hightower D W. A Solution to Line-routing Problems on the Continuous Plane[C]//Proc. of the 6th Annual Conference on Design Automation. New York, USA: ACM Press, 1969: 1-24.

[11] Zheng Siqing, Lim J S. Finding Obstacle- avoiding Shortest Paths Using Implicit Connection Graphs[J]. IE EE Transactions on Computer Aided Design, 1996, 15(1): 103-110.

[12] Wu Y F, Widmayer P. Rectilinear Shortest Paths and Minimum Spanning Trees i n the Presence of Rectilinear O bstacles[J]. IEEE Transactions on Computers, 1987, 36(3): 321-331.

[13] Zheng Siqing, Lim J S, Iyengar S S. Efficient Maze-running and Line-search Algorithms for VLSI Layout[C]//Proc. of Southeastcon’93. Charlotte, USA: IEEE Press, 1993: 275-282.

[14] 杨瑞元. 无网格线探索布线算法[J]. 计算机辅助设计与图形学学报, 1998, 10(3): 200-207.

[15] 蔡 毅, 王彦伟, 黄正东. 基于UG的三维电气自动布线技术研究[J]. 计算机工程与应用, 2012, 48(8): 68-72.

编辑 顾逸斐

New Algorithm for Point-to-Point Wiring Based on Boundary Expansion

LIAO Hai-tao, SHI Zheng, ZHANG Teng

(Institute of VLSI Design, Zhejiang University, Hangzhou 310027, China)

Global wiring is a very important step in the Very Large Scale Inte grated(VLSI) cir cuits design. Cla ssic maze routing algorithm and its improved versions are widely used to deal with global routing pr oblems in the in dustrial sector. With the dec reasing process node, the shortcoming of the high complexity of the maze routing algorithm becomes increasi ngly evident. By means of a new concept boundary expansion, this paper presents a new point-to-point wiring path search algorithm to solve the high complexity problem of rapidly increase with the expansion of the scale of routing. With the definition of free node, the new algorithm abandons the inefficient node by node expansion method. Instead, this algorithm expands the bo undary and finds ne w free nodes and will not terminat e until find out a path or determine that no solution is available. The theoretical and experimental comparisons are conducted between the proposed algorithm and classic routing algorithms. Experimental results show that the proposed algorithm can complete the routing wit h the runtime of 7%～14% of the classic algorithm in most cases.

Very Large Scale Integrated(VLSI) circuits; global wiring; maze routing algorithm; point-to-point wiring; boundary expansion; free node

10.3969/j.issn.1000-3428.2014.05.062

国家自然科学基金资助项目(61204111)。

廖海涛(1988－)，男，硕士研究生，主研方向：超大规模集成电路，计算机辅助设计；史 峥，副研究员、博士；张 腾，硕士研究生。

2013-04-15

2013-05-14E-mail：liaoht@vlsi.zju.edu.cn

1000-3428(2014)05-0299-05

A

TP312