地基干涉雷达变形监测信号静杂波去除方法研究
王 鹏,徐亚明,2,徐进军,2,肖 潇
(1.武汉大学测绘学院,湖北武汉 430079;2.精密工程与工业测量国家测绘地理信息局重点实验室,湖北武汉 430079)
地基干涉雷达变形监测信号静杂波去除方法研究
王 鹏1,徐亚明1,2,徐进军1,2,肖 潇1
(1.武汉大学测绘学院,湖北武汉 430079;2.精密工程与工业测量国家测绘地理信息局重点实验室,湖北武汉 430079)
一、引 言
地基干涉雷达(也称作雷达干涉仪)是最近10多年发展起来的地面主动微波遥感探测技术。它主要应用步进频率连续波(stepped-frequency continuous wave,SFCW)技术[1-2]获得天线辐射区域一维距离域的高分辨成像,一方面提高信号平均功率,从而增强接收天线的灵敏度,另一方面降低对高速数模转换器等硬件的需求,便于雷达系统的设计与实现,并最终利用微波干涉原理对采样信号之间的变形相位进行提取和计算。
国外学者在地基干涉雷达系统设计、信号处理及变形探测应用等方面作了大量研究。C.Farrar等较早地实现了利用干涉雷达进行大型结构的振动变形监测[3]。M.Pieraccini等利用干涉雷达进行了比萨斜塔、乔托钟楼等世界著名古迹的变形监测,也将其应用到风力发电塔群的变形监测中[4-6]。C. Gentile系统性地研究了干涉雷达在桥梁环境振动监测实验中的应用[7-9],利用雷达数据提取了桥梁结构的自振频率和模态振型,并与传统的加速度计等传感器测量分析的结果进行对比,充分验证了其在桥梁模态分析中的巨大应用价值。G.Luzi全面研究了干涉雷达在建筑结构健康监测中的应用[10]。相比之下,目前国内对于地基干涉雷达的研究尚处于变形监测应用与变形分析的初步阶段[11-15]。
由于监测环境和目标的复杂性,地基干涉雷达接收信号中会产生静杂波[16],不同于海杂波、地杂波等背景杂波,静杂波产生的主要原因是天线辐射范围内、同一个距离分辨单元多个独立散射体的相互作用,只能通过对监测信号的后处理进行分析和去除。静杂波的存在使测得的变形信号发生整体性偏移,直接影响结果的精度和可靠性。本文深入研究了地基干涉雷达形变监测信号中静杂波的产生原因、影响及其去除方法,有助于指导地基干涉雷达形变监测工作及形变信号的分析与解译。
二、地基干涉雷达变形监测基本原理
不同于脉冲体制雷达,SFCW技术通过发射以某一固定频率间隔Δf呈阶梯变化的连续波信号进行测量[17]。由于连续波不是无限长的,因此对应的是有一定脉冲宽度时域信号,对频谱作逆向傅里叶逆变换(IDFT),时域上等效载频为fm,周期为T的sin c函数,如图1所示。该聚焦过程使雷达在具有较窄瞬时带宽的同时,得到较宽的信号总带宽,形成了距离域的高分辨成像。
雷达传感器多次对辐射区域的监测目标进行采样,通过接收并分析回波信号的相位变化来计算形变量。利用地基干涉雷达进行变形监测的基本相位模型为

式中,Δφobs为实际观测相位;Δφdis为真实形变相位;Δφatm为气象扰动相位;φnoise为噪声相位。

图1 不同高分辨雷达信号处理方式
对于短时间(如20 min内)的监测,温度、湿度等气象参数变化较为缓慢,气象扰动项可以忽略;在较长时间(如60 min以上)的变形监测中,可将气象扰动视为空间和时间上的低频分量,利用高通滤波予以去除。噪声项由相位观测噪声和设备热噪声组成,可视为时间上的高频分量,一般采用低通滤波、小波分析等方法进行抑制。
视线向的形变量dlos与相位变化Δφobs满足以下关系

直接由干涉相位算得的dlos只是获取的雷达视线向的变形量,需要按实际的雷达基点与观测目标的几何关系转换到实际关注的变形方向。
三、变形监测信号静杂波的去除
1.静杂波的形成
地基干涉雷达接收机采用超外差和正交混频技术,将回波信号分解为同相(In-phase)分量和正交(Quadrature)分量,即IQ信号[16]。经聚焦处理,频域IQ信号转换为时域相位复信号,可以绘制在极坐标系中。目标的变形会直接影响相应分辨单元相位复信号的强度和相位值。
对于地基干涉雷达的一个距离向分辨单元(Range bin),其探测到的变形信号实际上是单元内所有散射体后向散射信号的矢量叠加。假设某分辨单元包含P1、P2、P33个独立的散射体,P1是监测目标,P2和P3相对保持静止。那么在采样时刻t1,由干涉雷达信号处理最终得到的是相应3个复矢量的矢量合。由于P2和P3同样形成后向散射回波信号并被天线接收,P1产生了一个常矢量偏移,即P2和P3的合矢量,如图2(a)所示。这一常矢量同样会影响后续各时刻的采样信号。由于独立静止散射体的存在,极坐标系下复信号的分布整体发生了一个常矢量的偏移,使得我们关注的变形目标回波信号的强度和相位均发生变化,这一常矢量称为静杂波相位分量或静杂波。
当雷达对监测目标进行连续采样,复信号在极坐标系下便形成一系列的离散点,这些点的变化轨迹包含了监测目标的变形信息。由上述静杂波的定义易知,可以通过对复信号点集拟合圆曲线来估计静杂波,即拟合圆曲线圆心偏离极坐标系原点的矢量,如图2(b)所示。
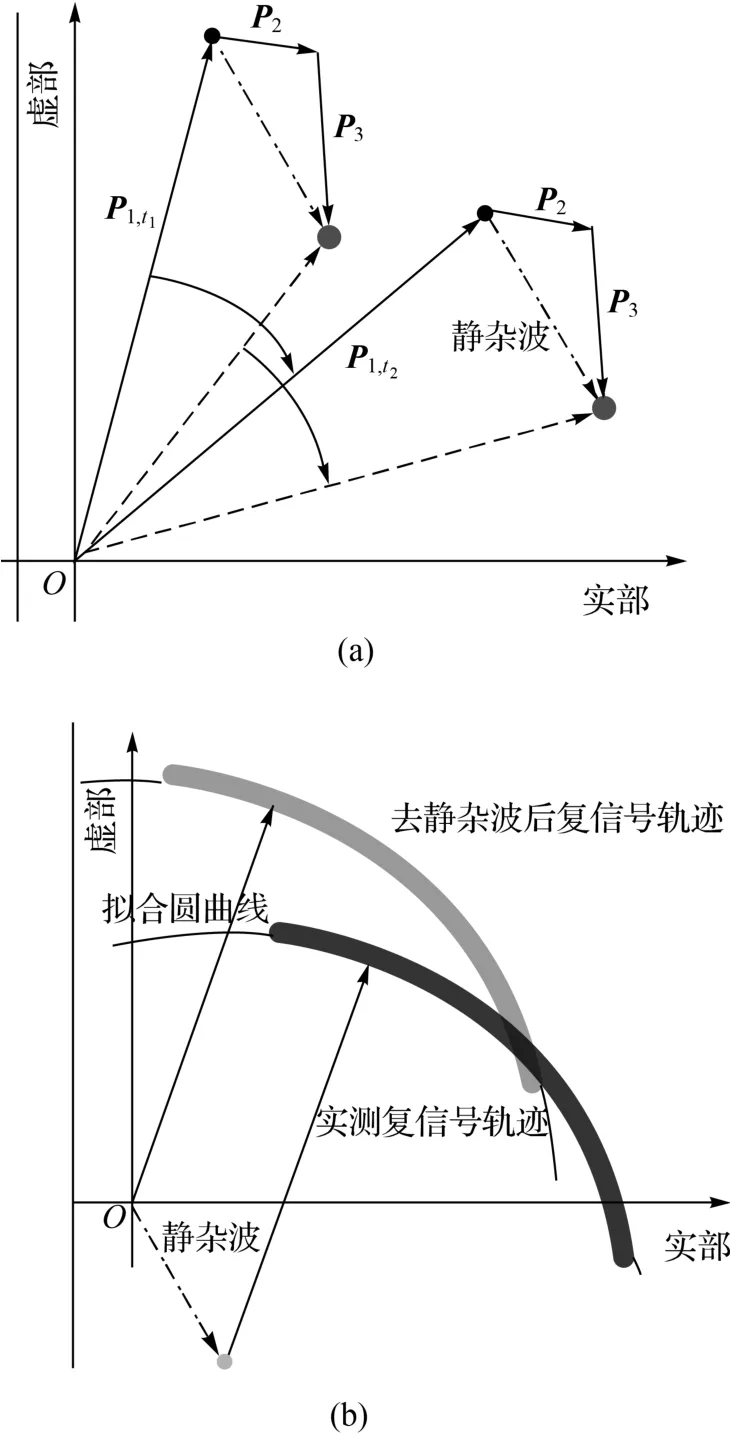
图2 静杂波的形成与去除
2.静杂波的去除方法
由上一节中的讨论得知,理想中形变散射体相应的相位复矢量末端轨迹应该位于以极坐标系原点为中心、以该形变散射体信号强度为半径的圆曲线上,静杂波的存在使得每个时刻采样的相位复矢量均加入了一个静杂波相位分量。因此,可以通过对实际得到的相位复矢量末端点拟合圆曲线来估计静杂波相位分量,即拟合圆曲线圆心偏离极坐标系原点的矢量。问题转变为极坐标系下离散点拟合圆曲线参数估计。
二维离散点的圆曲线拟合算法种类繁多,其算法效率、精度、稳定性和适用范围均有较大差异。几何拟合法以离散点到圆的几何距离最小为准则,该方法精度高,但需要迭代计算,易受粗差影响;代数拟合法以离散点到圆的代数距离最小为准则,计算快速,但精度稍差。考虑到研究使用的地基干涉雷达系统的稳定性很高,且在短时间内的热噪声非常有限,本文首先应用文献[18]中提出的梯度加权代数拟合近似方法确定圆曲线参数初值,再利用最小二乘迭代精确估计拟合圆曲线参数。
值得注意的是,如果分辨单元内散射体均保持静止,其相位复矢量数据在极坐标系的分布非常集中。由于拟合圆曲线参数估计方法本身的缺陷,难以正确地估计和去除静杂波相位分量,此时的形变目标无法从静杂波中分离出来。因此,目标形变需要有一定幅度,静杂波去除才能得到较为可靠和正确的结果,而对于形变幅度非常小的分辨单元通常不作静杂波估计和去除处理。
四、振动测量试验
本文试验使用地基干涉雷达系统IBIS-S和激光三维扫描仪Riegl VZ400进行。IBIS-S系统主要由雷达主机、PC控制单元、供电单元和三维旋转角架组成,能够获得0.5 m的距离向分辨率,通常情况下容易探测到目标区域亚毫米级的形变,在500 m范围内雷达视场较好情况下能够达到0.01 mm的形变监测精度[2]。VZ400的线扫描模式也具有较高的采样率,近距离的测量精度较高,能够获取目标多个部位的形变值。
试验在室内进行,监测目标为一个长1 m、宽0.03 m的钢条片,竖直放置在一个稳定的平台上,并将其底端固定在平台上。人为拨动钢条上边缘使之开始摆动,利用IBIS-S和VZ400同时对钢条摆动形变进行监测。钢条的摆动是一个逐渐衰减的振动过程,且顶端形变幅度最大,越向底端形变幅度越小。
将试验获取的相位复矢量采样数据绘制在极坐标系下,在去除静杂波相位分量之前(如图3(a)所示),可以看到采样相位复矢量数据的分布是一个逐渐向中心收缩的螺旋线,信号强度随钢条的形变幅度逐渐减小,但螺旋线的几何中心与极坐标系原点有非常明显的偏差。经过圆曲线参数估计去除静杂波之后,相位复矢量数据散点分布如图3(b)所示。
计算IBIS-S监测数据静杂波去除前形变趋势及其频谱图,如图4(a)―(b)所示。计算去静杂波后形变趋势及其频谱图,如图4(c)―(d)所示。提取扫描仪线扫描测量数据中位于钢条顶端的形变数据,计算其频谱图,如图4(e)―(f)所示。比较时序形变图和频谱图易看出,未经静杂波相位分量去除的形变趋势变化异常,且频谱图中出现多个全局和局部峰值,不符合实际情况。扫描仪提取的形变波动递减的趋势与干涉雷达数据去杂波后的结果是非常一致的。而其频域全局峰值均只有一个。

图3 静杂波去除前后相位复矢量采样点分布
雷达和扫描仪位置不能完全重合,且两者数据记录起始时刻无法严格统一,使得形变幅度略有差别。另外,由于VZ400没有给出精确时间记录,无法精确确定其采样频率,扫描仪计算出的自振频率和IBIS-S形变数据计算的结果也存在一定偏差,由去杂波的雷达数据算得的一阶固有频率为1.648 1 Hz,而由扫描仪数据算得的一阶固有频率为1.699 1 Hz。但其形变趋势已经说明了静杂波去除后的形变计算结果的正确性。由此可见,静杂波的存在不仅影响强度信息,而且影响形变的时序特征和频谱特征,在干涉雷达形变信号的分析中需要对其进行估计和去除。

图4 形变趋势及其频谱分析
五、结束语
本文揭示了地基干涉雷达静杂波相位分量去除问题的实质,即极坐标系下离散点拟合圆曲线参数估计。地基干涉雷达系统IBIS-S和三维激光扫描仪Riegl VZ400线扫描模式的振动测量对比试验,说明了干涉雷达信号中静杂波的存在不仅影响强度信息,而且影响形变的时序特征和频谱特征。在实际应用地基干涉雷达系统进行监测工作中需要分析并合理去除静杂波相位分量,以确保监测数据的正确性和高精度。在目标形变过程中,信号强度并不是完全不变的,可以依据形变的大小对强度信息进行修正,以提高静杂波相位分量估计的精度,这是今后值得研究的方向。
[1]PIERACCINI M,TAICHI D,RUDOLF H,et al.Structural Static Testing by Interferometric Synthetic Radar [J].NDT&E International,2000,33(8):565-570.
[2]PIERACCINI M,FRATINI M,PARRINI F,et al. High-speed CW Step-frequency Coherent Radar for Dynamic Monitoring of Civil Engineering Structures[J].E-lectronics Letters,2004,40(14):907-908.
[3]FARRAR CR,DARLING TW,MIGLIORI A,et al.Microwave Interferometers for Non-contact Vibration Measurements on Large Structures[J].Mech Syst Signal Process,1999,13(2):241-253.
[4]PIERACCINI M,FRATINI M,DEI D,et al.Structural Testing of Historical Heritage Site Towers by Microwave Remote Sensing[J].Journal of Cultural Heritage,2009,10(2):174-182.
[5]ATZENI C,BICCI A,DEI D,et al.Remote Survey of the Leaning Tower of Pisa by Interferometric Sensing [J].IEEE Geoscience and Remote Sensing Letters,2010,7(1):185-189.
[6]PIERACCINI M,PARRINI F,FRATINI M,et al.Inservice Testing of Wind Turbine Towers Using a Microwave Sensor[J].Renewable Energy,2008,33(1):13-21.
[7]GENTILE C.Deflection Measurement on Vibrating Stay Cables by Non-contact Microwave Interferometer[J]. NDT&E International,2010,43(3):231-240.
[8]GENTILE C,BERNARDINI G.Output-only Modal Identification of a Reinforced Concrete Bridge from Radarbased Measurements[J].NDT&E International,2008,41(7):544-553.
[9]GENTILE C,BERNARDINI G.An Interferometric Radar for Non-contact Measurement of Deflections on Civil Engineering Structures Laboratory and Full-scale Tests [J].Research in Nondestructive Evaluation,2009,6(5):1-14.
[10]LUZI G,MONSERRAT O,CROSETTO M.The Potential of Coherent Radar to Support the Monitoring of the Health State of Buildings[J].Research in Nondestructive Evaluation,2012,23(3):125-145.
[11]徐亚明,王鹏,周校,等.地基干涉雷达IBIS-S桥梁动态形变监测研究[J].武汉大学学报:信息科学版,2013,38(7):845-849.
[12]黄声响,罗力,何超.地面微波干涉雷达与GPS测定桥梁挠度的对比试验分析[J].武汉大学学报:信息
Research on Static Clutter Removal of Deformation Signal Obtained by Ground-based Interferometric Radar
WANG Peng,XU Yaming,XU Jinjun,XIAO Xiao
简要介绍地基干涉雷达用于形变监测的基本原理,论述地基干涉雷达观测信号中静杂波的产生原因及其去除方法。结合地基干涉雷达系统IBIS-S与三维激光扫描仪Riegl VZ400线扫描模式的振动测量对比试验,说明地基干涉雷达静杂波对形变监测信号的影响及去除静杂波的必要性。
地基干涉雷达;步进频率连续波;静杂波;振动测量
P237
B
0494-0911(2014)10-0015-04
2013-09-04
精密工程与工业测量国家测绘地理信息局重点实验室开放基金(PF2011-8);国家自然科学基金(41274021);中央高校基本科研业务费专项资金青年教师资助项目(121077)
王 鹏(1986―),男,江苏睢宁人,博士生,研究方向为精密工程测量、星载与地基InSAR地表变形监测应用研究。
王鹏,徐亚明,徐进军,等.地基干涉雷达变形监测信号静杂波去除方法研究[J].测绘通报,2014(10):15-18.
10.13474/j.cnki. 11-2246.2014.0318

