从气旋和反气旋谈正、负阻尼

刘式达 刘式适 付遵涛



从气旋和反气旋谈正、负阻尼

刘式达 刘式适 付遵涛

北京大学物理学院大气与海洋科学系气候与海—气实验室，北京100871

在定常条件下，利用简化的大气运动控制方程，分析了气旋与反气旋的基本特征。在此基础上，利用常微分方程的定性分析与求解，获得了气旋和反气旋轨道的解析解。接合气旋与反气旋的基本特征，论证了正负阻尼在气旋和反气旋运动中具体体现，并从物理机理上说明产生气旋和反气旋运动中正负阻尼的差异在于水平辐合在低层的不同。

正阻尼 负阻尼 气旋 反气旋 轨道

1 引言

很多人往往把阻尼、耗散的概念和摩擦力联系在一起，实际上，这是两个不同的概念。力学上是说，当相互接触的物体做相对运动时，它们之间就有摩擦力，它的大小和速度成正比，但方向相反（赵凯华，罗蔚茵，1995），即

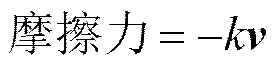
其中＞0称为摩擦系数，是速度向量。

而阻尼和耗散这两个概念通常是与系统联系在一起的。例如流体力学中的不可压缩流体的质量守恒定律（也称作连续方程）可以表示为（Milne- Thomson，1960）

速度散度div的物理意义是单位体积的体积流量。方程（1）就表示单位时间流出去的体积等于流进来的体积，因而就说该系统是守恒系统。

但是若单位时间内流出去的少流进来的多，那么该系统中间就要有一部分流体被耗散掉了，此时

div＜0, （3）

那么就称该系统是耗散系统或阻尼系统（Ott，1993，Arnold et al., 1983）。

但是，若流出去的多，流进来的少，此时速度散度

div＞0. （4）

那么该系统称为什么呢？至少局部若有（4）式成立，就称为负阻尼或负耗散的系统。正如D.Y. Hsieh在他的著作“wave and stability in fluids”所述，负阻尼是动力系统三种不稳定的机制之一（Hsieh，1994）。

大气科学中的气旋和反气旋是涡旋，正是论述正负阻尼的范例。在气压梯度力、科氏力和摩擦力三力平衡时，气旋、反气旋的斑图均是螺旋（刘式达，刘式适，2011）。螺旋的中心均是速度场为零的焦点。气旋的中心是稳定焦点，在北半球，轨道由外向内逆时针旋转。而反气旋的中心为不稳定焦点，轨道由内向外顺时针旋转。因此气旋是正阻尼系统，反气旋是负阻尼系统。下面我们来论证这一点。

2 气旋、反气旋的特征

在定常情况下，在气压梯度力、科氏力和摩擦力相互平衡的大气运动方程为（刘式适，刘式达，2011）

将（5）式的第一式对求导，第二式对求 导，然后相加得到

其中

, （7）

是垂直涡度。

将（5）式的第一式对求导，第二式对求导，然后相减得到

（6）式是Poisson方程，若假设气旋或反气旋的垂直涡度是常数，水平散度也是常数，那么方程（6）的解是

, （9）

将（9）式代入（5）求得

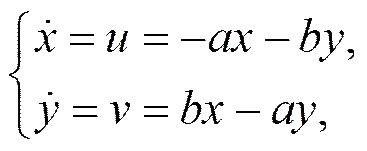
其中

（11）

从（8）式看出，因为和都是正常数，因而垂直涡度和水平散度符号相反。这正符合气旋、反气旋的特征。在北半球，气旋是正涡度＞0，地面的水平散度＜0；反气旋是负涡度＜0，地面的水平散度＞0。

由（9）式看出，等压线是一个圆形，这也符合气旋、反气旋的实际情况。

由（6）式看出，对于气旋

这表示周围的气压值大于中心的气压值，因而中心为低压。类似，对于反气旋

＜0, （13）

这表示周围的气压值小于中心的气压值，因而中心为高压。

由（11）式看出，对于气旋＞0，＞0；对于反气旋＜0，＜0。

所以归纳讲，北半球气旋、反气旋的特征如表1。

表1 北半球气旋、反气旋的特征

3 正、负阻尼

上节说明，用三力平衡方程（5）描述的气旋与反气旋正好确切地反映了气旋和反气旋的主要特征。

我们将（10）式的第一式对时间求导并用第二式代入得到

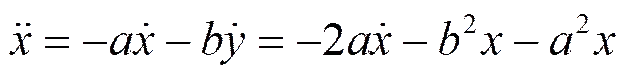
即

, （14）

（14）的解为

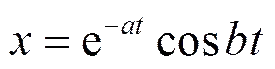
从（15）式看出，常数表示振荡频率，阻尼系数＞0时，随着时间的增加，振幅衰减；而阻尼系数＜0时，随着时间的增加，振幅增大。

所以对于气旋（＞0）而言，它的轨道是振幅随时间衰减的振荡，那当然是阻尼振荡；而对于反气旋（＜0）而言，它的轨道是振幅随时间增大的振荡，那当然是负阻尼振荡（Starr，1968）。

气旋与反气旋的特征性行为见图1a和b。在图1中实线表示轨道，箭头表示时间增加的方向。在轨道上取一小面积元，那么对于气旋的正阻尼系统，小面积元随时间不断收缩；而对于反气旋，小面积元随时间不断扩展。这正是正、负阻尼振荡的区别所在。

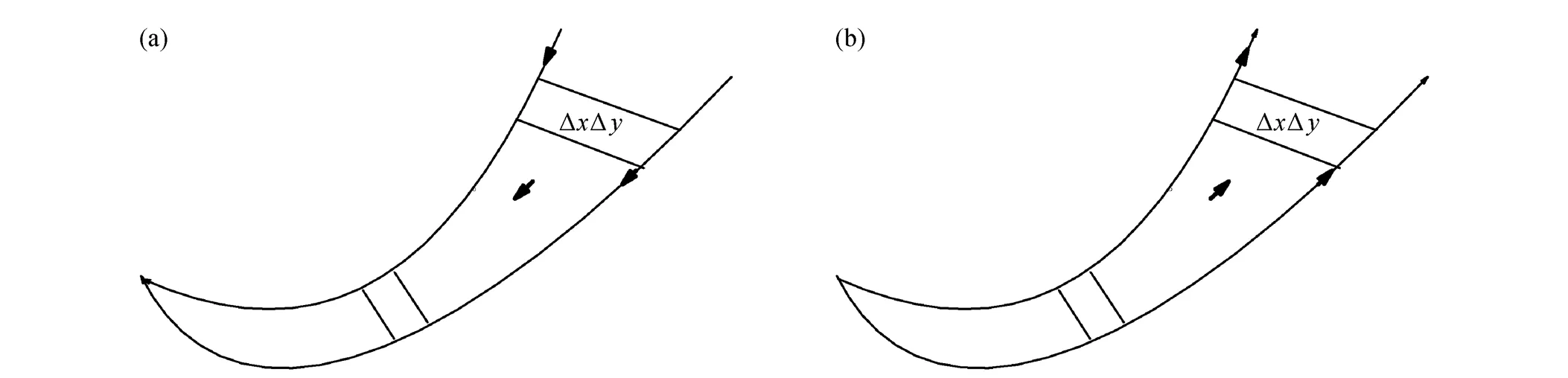
图1 （a）气旋和（b）反气旋的轨道示意图

这种正、负阻尼的差别的物理因素是什么呢？从物理上讲，由（11）式看出，主要是水平散度的差别。对于气旋＞0，地面的水平散度＜0，它意味着流进来的多，流出去的少，见图1a，那当然是耗散系统或正阻尼系统。此时若无外源提供能量，那么它的轨道就要收缩到焦点吸引子。实际上大气运动是三维的，它满足的是三维连续方程（2）式。当＜0时，由（2）式得到＞0，由于地面= 0处= 0，因而必然引起上升运动。所以尽管从水平面上看流进的多，流出去的少。但是这种“外源”使得水平方向的耗散由垂直方向的上升运动来“补充”，从而使得流出的量增多，它不会停留在焦点“不动”。而由上升运动补充流出，最后达到流进来与流出去的平衡。

对于负阻尼的反气旋，由图1b看出，由于地面水平散度＞0，即水平辐散。轨道上的小面积元随时间增大，即流进来的少，流出去的多。哪里多出来的“大气”流出呢？原来连续性方程（2）也告诉了我们。当＞0时必然有＜0，也就是产生下沉运动，它补充了“流进来”的不足。也就是说，“大气的下沉运动”使得空气团体积压缩，外界对内做功，使得下沉的空气团内能增加转变成动能，这就是负阻尼的一种“力”。所以，反气旋在水平方向上负阻尼的驱动力是下沉运动，它驱使大气螺旋向外。

Arnold V I, Levi M, Szücs J. 1983. Geometrical Methods in the Theory of Ordinary Differential Equation [M]. New York: Springer-Verlag.

Hsieh D Y. 1994. Wave and Stability in Fluids [M]. Singapore: World Scientific.

刘式达, 刘式适. 2011. 大气涡旋动力学 [M]. 北京: 气象出版社. Liu Shida, Liu Shikuo. 2011. Dynamics of Atmospheric Eddy (in Chinese) [M]. Beijing: China Meteorological Press.

刘式适, 刘式达. 2011. 大气动力学 [M]. 北京: 北京大学出版社. Liu Shikuo, Liu Shida. 2011. Atmospheric Dynamics (in Chinese) [M]. Beijing: Peking University Press.

Milne-Thomson L M. 1960. Theoretical Hydrodynamics [M]. London: Macmillan.

Ott E. 1993. Chaos in Dynamical Systems [M]. Cambridge: Cambridge University Press.

Starr V P. 1968. Physics of Negative Viscosity Phenomena [M]. New York: McGraw-Hill.

赵凯华, 罗蔚茵. 1995. 力学 [M]. 北京: 高等教育出版社. Zhao Kaihua, Luo Weiyin. 1995. Mechanics (in Chinese) [M]. Beijing: Higher Education Press.

刘式达, 刘式适, 付遵涛. 2014. 从气旋和反气旋谈正、负阻尼[J]. 大气科学, 38 (6): 1041−1043, doi:10.3878/j.issn.1006-9895.2013.13259. Liu Shida, Liu Shikuo, Fu Zuntao. 2014. Positive and negative damping in cyclones and anticyclones. [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 38 (6): 1041−1043.

Positive and Negative Damping in Cyclones and Anticyclones

LIU Shida, LIU Shikuo, and FU Zuntao

,,,100871

Under steady conditions, simplified control equations of atmospheric motion are used to analyze the basic characteristics of cyclones and anticyclones. On this basis, analytic solutions of cyclonic and anti-cyclonic trajectories are derived by qualitatively analyzing and solving ordinary differential equations. By combining the basic characteristics of cyclones and anticyclones, it is demonstrated that positive and negative damping behaviors are present in cyclonic and anti-cyclonic motions and that the physical mechanism of the negative damping in these motions results from various types of horizontal convergence at low levels.

Positive damping, Negative damping, Cyclone, Anticyclone, Trajectory

1006−9895(2014)06−1041−03

P432

A

10.3878/j.issn.1006-9895.2013.13259

2013−09−06，2013−11−08收修定稿

国家自然科学基金项目40975027

刘式达，男，1938年出生，教授，主要从事大气湍流与非线性大气动力学研究。E-mail: liusd@pku.edu.cn

付遵涛，E-mail: fuzt@pku.edu.cn