改进PCA和JADE盲源算法应用于电机系统振动信号的分离

李秀梅 李 文 孙燕楠 曲英伟

(1.大连交通大学软件学院，辽宁 大连 116052；2.大连交通大学动车学院，辽宁 大连 116028)

为了研究电机系统振动抑制以及电机故障的预测和诊断，笔者从电机系统实测振动信号着手，在不破坏、不干扰机器正常运行的前提下，采用盲源分离(Blind Signal Separation，BSS)算法对电机系统振动实测信号进行分离，从几个独立于传播介质的观测信号中初步估计出振动源信号的数目和振动源信号在不同频率段的分布情况。利用BSS处理信号可以作为系统故障诊断的预处理步骤，也可为电机系统振动抑制算法和电机故障分析提供理论依据。

以往采用BSS分离混合信号的前提是观测信号是无噪声的，即使有噪声也是空间白化噪声，因为带噪声的BSS算法首先采用主分量PCA(Principal Components Analysis)技术滤除噪声、白化观测信号[1]，尽可能使源信号之间不相关。PCA估计信号子空间的第一步是需要计算观测信号的协方差噪声矩阵，然后对此矩阵进行特征值(Eigen Value Decomposition，EVD)分解，将观测信号投影到不相关的信号子空间，但此时得到的信号仍然是源的混合信号。随后利用更强的相互独立性约束准则去分离、恢复源信号。从中可见，整个分离过程的有效性取决于第一步信号预处理PCA。但是，在现实世界中，电机系统振动信号很可能已经被来自噪声环境的空间相关噪声严重污染，如果仍按照上述方法处理信号，就不能正确估计信号子空间，在这种实验环境下，PCA丢失了有效性，从而随后的BSS算法就变得不再可靠。

为了解决上述问题，增强算法应用的鲁棒性，笔者采用了改进PCA对振动信号进行预处理，然后利用JADE(Joint Approximate Diagonalization of Eigenmatrices)算法对电机系统振动信号进行源分离，提取出主要源振动信号。研究结果表明：用改进的PCA和JADE算法可以从混杂的信号中较为清晰地分离出主要源信号，通过对不同频段源信号的分析，可以初步确定源信号的一些特征。

1 PCA改进算法①

振动信号通常附带空间相关噪声干扰，因此笔者采用了改进的PCA处理空间相关噪声系统，下面描述改进的PCA算法原理。假设从旋转电机测得的源信号呈周期性，它们的自相关长度也是周期的、无限的；且假设源信号的自相关长度总是大于所有噪声的自相关长度。由此排除了空间干扰噪声的影响，对空间相关噪声有一定的鲁棒性。从而实现了由延迟观测信号谱矩阵构建源信号无噪声谱矩阵[2]。

延迟谱矩阵定义为[3]：延迟时间段τ的谱矩阵，就是观测信号X(n)和延迟观测信号X(n+τ)的延迟谱矩阵，对于单维信号，称为自相关频谱。

(1)

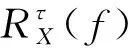
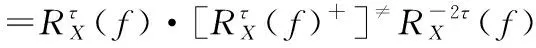
=V(f)·Δ(f)·V(f)+

(2)

根据以上结论，采用改进的PCA对电机振动信号进行预处理，随后采用JADE算法对预处理后的信号在更强的独立性约束准则下进行分离[4]，算法的性能在分离电机系统振动信号实验的结果中进行验证。

2 电机系统振动源信号的分离

2.1 电机调速系统振动信号的采集

由于电机的振动信号蕴含着丰富的运行状态信息，具有一定的物理含义，其特征值与故障往往有着很强的对应关系，而且可以在不影响电机运行的情况下实时在线采集信号，根据振动信号分离结果预测、分析电机系统的运行状况，故常常用系统中的振动信号来对系统进行监测和诊断。

安装在机械设备上的振动传感器所测得的信号不仅包含其他机械的振动，也包含自身零部件产生的振动，为了获得良好的振动信号，必须解决好检测点的选择问题，检测点选择的总原则是：将检测点选择在离轴承最近，能直接反应轴承-振动的位置上。本实验系统由两台物理上不相连、电气上相连的电机组成，电机实验系统主要由发电机和电动机构成，数据采集系统由4个加速度传感器构成。为确保能够采集到电机系统中更多的包含振动源的振动信号，经过多次尝试，选择检测点的位置如图1所示，在电机系统的电机和发电机轴的水平方向和垂直方向分别安装两个加速度传感器，由这4个加速度传感器对电机系统进行振动信号的采集。

图1 加速度位置

具体实验中采集数据时，系统的电动机转速为600r/min，数据采样频率12.8kHz，连续采样5s的数据长度为64 000，从采样数据中选取连续的一个多采样周期的数据。本实验选取了15 512个采样点。4路信号的频域功率谱图如图2所示，可以看出振动信号有很明显的混合现象。

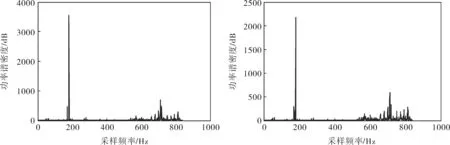
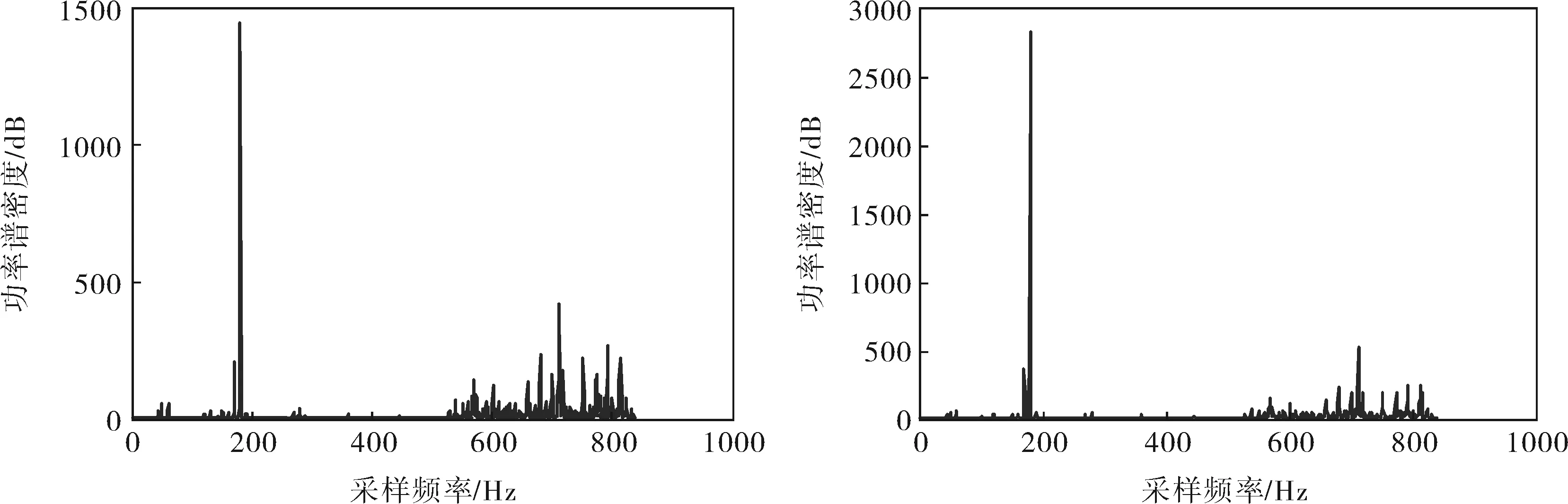
图2 4路测量信号的频域功率谱图

2.2 振动源信号的分离与分析

一般实测的电机系统振动信号都含有噪声，故采用延迟频谱矩阵来降低系统中的噪声，对4路传感器采集来的混合信号，采用改进PCA对数据进行去噪、降维处理，处理过程中采样数据的99.72%以上的主要特征值被保留下来。处理后，使混合信号的各个分量之间的独立性尽可能最大化、相关性最小。为了使分离后的各个源信号之间独立，采用四阶累积量作为独立性约束准则的JADE算法进行分离计算，分离后能够提取出3个能量特征比较明显的独立分量。计算过程中表现出收敛速度快、鲁棒性强及分离效果好等特性。

根据分离后的独立分量得到其频域图(图3)，图中很好地将各个频段部分的主要源信号进行分离，已经明显消除了发电机和电动机振动信号的混叠现象。

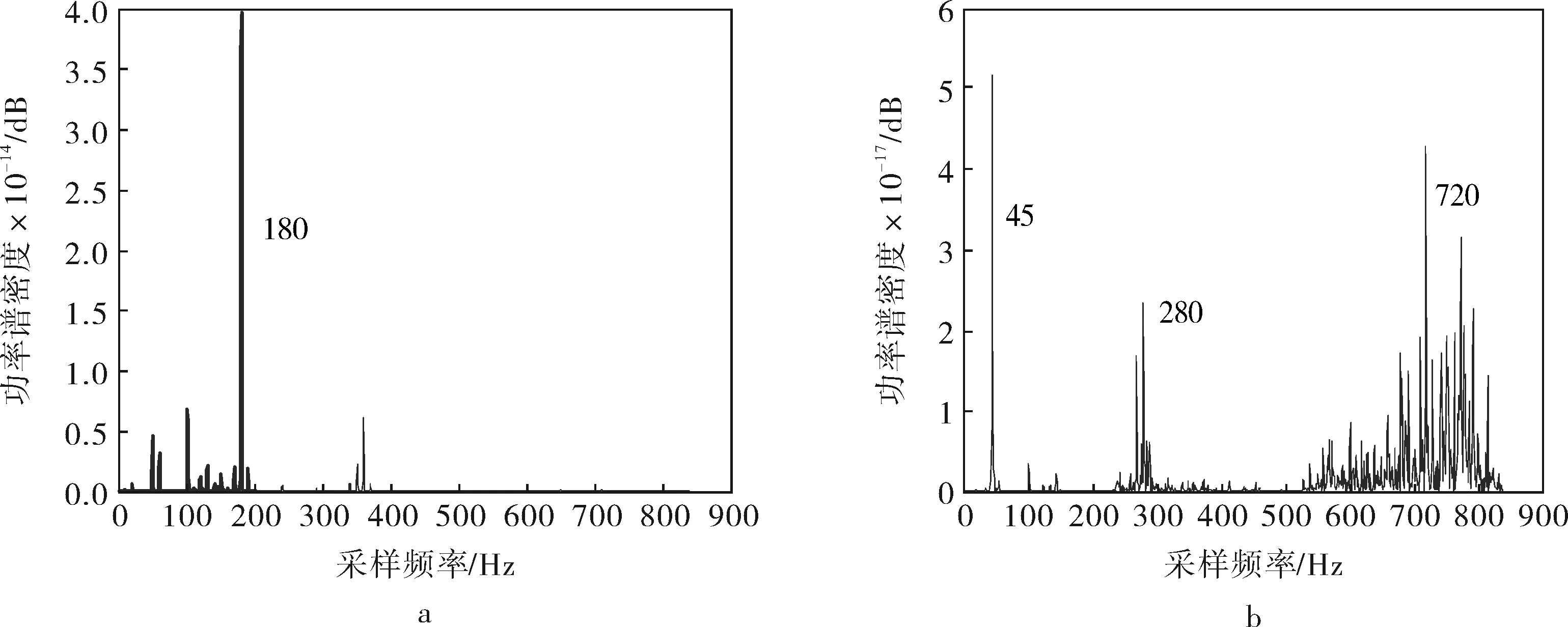
图3 分离后源信号频域功率谱图

图3c中含有主要频段600～800Hz的振动源信号，分离出的源信号以712Hz处的峰值为主要源信号；图3b中分离出的源信号以45、280、720Hz点附近的峰值为主要振源，处于600～800Hz频段的部分峰值为主要源信号；图3a中分离出的源信号以180Hz处的峰值为主。分析分离后信号的频域图，发现本电机系统中分离后的振动信号主要集中在600～800Hz频段部分，其中包含712Hz处峰值对应的频率点。根据文献[5]，当电机处于转速稳定状态时，轴承的振动有3种类型：与轴承固有特性有关的振动、与轴承制造有关的振动、与轴承使用有关的振动，而在实验中比较关心的是与轴承使用有关的振动，它由固有振动和低频脉动组成，如处于低频段45Hz属于低频脉动振源；180、280Hz处振动信号可能与滚动轴承自转和公转频率有关；而600～800Hz频段内有明显的峰值，这类噪声属于轴承元件的特征频率或其高次谐波。

3 结束语

采用改进PCA和JADE盲源算法，对电机调速系统振动实测信号进行了分离，得到3个主要源信号，分别是频段600～800Hz附近振动源信号、频段45Hz和280Hz振动源信号。通过分离结果可以看出，该算法可以很好地将实测信号的各频段部分主要振动源进行分离。并发现，分离后的各个信号在频域的独立性特征明显地体现出来。分离实验和结果说明：对电机这类旋转机械系统的周期性、带噪声的振动信号，将改进PCA和JADE盲源算法应用于电机系统振动信号分离效果较好，且算法具有一定的鲁棒性。