基于势函数的多智能体避撞队形控制
姚立强,宋艳荣,张术东
(1. 烟台大学数学与信息科学学院,山东 烟台 264005; 2. 海军航空工程学院系统科学与数学研究所,山东 烟台 264001)
多智能体系统是控制领域的一个热点研究方向.队形控制是多智能体系统控制中的一类重要问题.队形控制是指多个移动智能体在前进过程中,整个智能体系统实现并维持预先给定的队形,同时又要适应环境约束的控制技术.队形控制问题属于多智能体系统的几何问题[1].现实生活中,队形控制广泛应用于多移动机器人编队[2]、自治水下无人机组[3]、人造卫星[4]、航天器等的协作中.
近年来,随着队形控制问题研究的深入,提出了多种队形控制策略,主要包括Leader-follower法、Virtual structure 法、Behavior-based法和Artificial potential field法等.文献[5]研究了在通信拓扑结构固定条件下,利用智能体之间的相对位置信息,设计反馈控制律,实现了对无领导者的多智能体系统队形控制问题.郑军将文献[5]的结论推广到离散系统[6],得到了确保多智能体系统渐近收敛的充要条件和反馈控制参数的取值范围.文献[7]对单积分模型系统,利用多智能体之间相对位置的测量,提出了基于分布式位置估计的队形控制策略.文献[8]研究了在跟随者未知参考速度的情况下,基于相对位置信息,利用自适应方法设计动态反馈控制器,使得系统实现期望队形.
本文主要利用人工势场法对无领导者的多智能体系统进行队形控制问题研究.对目前现有文献中运用的避撞势函数进行一定程度的改进,使势函数的形式更加简洁,更易于构造,并运用所提出的势函数方法研究多智能体系统的队形控制问题,并且要求在形成期望队形的过程中,智能体之间避免发生碰撞.
1 问题的提出
考虑一类由N个智能体组成的多智能体系统,第i(i=1,2,…,N)个智能体的位置模型如式(1)所示
(1)
其中:qi∈Rn是智能体i的位置向量,ui∈Rn是控制输入.
注1 该系统是典型的分布式控制系统.控制的目的就是在给定智能体通信规则的基础上建立互相协作的控制策略,实现队形控制目标.
注2 本文研究无领导者多智能系统避撞队形控制问题,信息接收方式是基于通信和避撞感知的,这里通信的拓扑结构固定,避撞感知拓扑结构是变化的.
为了更好地描述多智能体系统的队形控制问题,我们引入以下定义.
定义1[9](基于通信的智能体的邻居集) 在由N个智能体组成的多智能体系统中,如果智能体i可以接收并利用智能体j的信息,则称智能体j是智能体i的邻居.由智能体i的所有邻居组成的集合Ni(i=1,2,…,N)称为智能体i的邻居集.
定义2[9](避撞感知半径) 在基于感知的多智能体系统中,为了实现智能体之间的避撞目的,智能体i与其能够接收并利用信息的智能体之间距离的最大值称为智能体i的避撞感知半径,记为Ri.
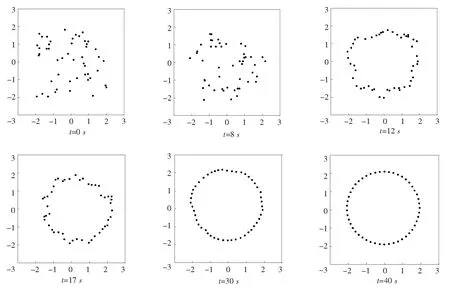
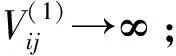
定义3[9](基于感知的智能体的邻居集) 如果多智能体系统中的智能体j位于智能体i的避撞感知区域内,即2个智能体的相对位置满足‖qi-qj‖ Nαi={j|‖qi-qj‖ j≠i;j=1,2,…,N} (i=1,2,…,N) (2) 称为智能体i的邻居集. 智能体之间的避撞控制目标用数学形式可以描述为 ∀t>0, ‖qi(t)-qj(t)‖→/ 0. (i≠j;i,j=1,…,N) (3) 描述智能体的队形以一组向量来表示,我们称这组向量为期望队形.为了清楚地描述队形,引入期望队形的定义,并根据期望队形给出多智能体系统实现队形控制的目标. 定义4[6](期望队形) 期望队形就是某个向量h=col(h1,h2,…,hN),其中hi是智能体i相对某个参照点的相对位置. 如果多智能体系统中任意智能体的位置向量满足 qi-qj=hi-hj.(i≠j;i,j=1,2,…,N) 则称多智能体系统实现期望队形h.等价地,如果存在r(t)使得 qi=r(t)+hi.(i=1,2,…,N) (4) 则称多智能体系统实现期望队形h. 注3 期望队形中两智能体之间的距离总是大于它们的避撞感知半径. 若记智能体通信拓扑对应的无向图为G,智能体避撞感知拓扑对应的无向图为Gα.本文控制问题可以描述为:在给定通信拓扑G的条件下,建立基于通信拓扑的协作控制输入ui,使得多智能体系统(1)满足避撞控制目标(3)和队形控制目标(4). 令G=(ν,ε)表示带n个节点的图,其中ν={v1,v2,…,vn}为节点集合,ε⊆ν×ν为边集合.如果节点i和节点j之间存在信息交互,则这2个节点有边相连.在无向图G中,如果任意2个节点间都有路径,则称无向图G是连通的. 为了描述节点与边的关系,对于有n个节点的无向图G,我们可以定义邻接矩阵A(G)=[aij](i,j=1,2,…,n)为 对于无向图,邻接矩阵A是对称的,对于有向图,该矩阵不具备这样的性质. 图G的Laplace矩阵L=[lij](i,j=1,2,…,n)定义为L=ΔG-A(G). 引理1[10]无向图G的Laplace矩阵L具有以下性质 1)L是对称的且半正定;0是矩阵L的特征值,其对应的特征向量为1N; 2) 如果无向图G是连通的,则0是矩阵L的代数重度为1的特征值; 3) 根据Gershgorin圆盘定理,L的所有特征值位于一个以Nmax为半径的圆盘中(其中Nmax是图G中顶点的最大邻居数). 队形控制对智能体的相对位置有特定的要求,所以必须构造相应的势函数,该势函数能产生指向相对位置的“力场”驱使智能体实现相对位置,使得整个系统进入平衡状态.否则,“力场”会一直发挥作用,直至整个系统进入平衡状态. 定义5(位置匹配势函数生成函数) 与给定的向量h匹配的势函数生成函数V(x,h)是一个非负、连续可微的函数,且满足 1)V(x,h)=V(-x,-h); 2)V(x,h)=0成立当且仅当x=h; 3) 当‖x-h‖→∞时,V(x,h)→∞. 注4 位置匹配势函数可以取为V(qi-qj,hi-hj).为了区分不同智能体的位置匹配势函数,我们用Vij(qi-qj,hi-hj)表示智能体i和智能体j之间的位置匹配势函数,简记为Vij. 当2个智能体之间的距离很小时,2个智能体之间会产生“力场”,该“力场”使智能体能够向着距离增大的方向运动就可以解决智能体之间的避撞问题.我们将“力场”作用在智能体上的力称为反作用力.与智能体i产生反作用力相关的特定值就是智能体i的避撞感知半径的大小. 注5 避撞势函数生成函数中的a就是智能体i的避撞感知半径Ri. 注6 避撞势函数要比现有文献中已有的避撞势函数形式简洁得多. 证明定义智能体i总的避撞势函数为 (5) 定义智能体i总的位置匹配势函数为 (6) 定义多智能体系统(1)总的能量W为系统智能体总的位置匹配势函数和避撞势函数之和,简称能量函数.它的表达式如下 (7) 从能量函数W的表达式可以知道该函数是一个半正定的函数,并且 (8) 设计智能体i的控制输入的形式为 (9) 由于 (10) (11) 将式(9)、(10)、(11)代入式(8)中,得到 (12) W(t)≤W0. (13) qi-hi=qj-hj. (i≠j;i,j=1,2,…,N) (14) 即 (15) 其中:L是图G的Laplace矩阵. 即 qi=r(t)1n+hi. (i=1,2,…,N) (16) 这样,由式(16)可知,在控制输入(9)的作用下,多智能体系统(1)最终形成预先给定的期望队形,从而实现队形控制目标(4). 为了实现避撞控制目标(3),需要证明系统中的智能体在任何时刻都不会发生碰撞.下面,用反证法来证明这个问题. 假设多智能体系统中至少有2个智能体r和e在时刻t1>0相撞,即r和e在时刻t1的位置满足 qr(t1)=qe(t1), (r≠e;r,e=1,2,…,N) 由避障势函数定义和式(5)可知 由于t=t1时,qr(t1)=qe(t1),即t→t1时有 (17) 另一方面,由式(7)、定义5、定义7可知 (18) 由于系统总的能量W0为有限数,这样式(18)和(17)产生矛盾.说明假设错误,即多智能体系统在行进过程中智能体之间不会发生碰撞. 由上面的分析可知,在设计的控制输入(9)的作用下,多智能体系统(1)可以实现避撞控制目标(3)和队形控制目标(4).证毕. Vij=(qi-qj-hi+hj)T(qi-qj-hi+hj). (i≠j;i,j=1,2,…,49) 选取的避撞势函数为 其中:qi=(xi,yi)T,Ri是智能体i的避撞感知半径,Ri=0.2. 仿真中发现,位置匹配势函数的权重系数影响反馈的增益,较大的权重会使智能体的队形对齐速度加快,较小的权重则可以使速度变慢.这里为了得到理想的仿真效果,对位置匹配势函数做了调整,令其前面的权重为0.051,避撞势函数的权重为1. 当49个智能体的初始位置在[-2,2]×[-2,2]的区域内随机选取、通信拓扑在保证连通的前提下随机指定时,仿真结果如图1所示. 从图1中的6幅图中可以看出,初始时刻49个智能体是杂乱无章的,第8秒时智能体分散开向着圆形队形的方位运动,到第17秒时智能体基本到达期望队形区域,最终在第40秒实现圆形队形.从仿真结果可以看出,智能体在位置匹配势函数产生的力场的作用下,向着指定位置逼近,最终会进入事先指定的队形,即实现队形控制目标. 注7 仿真中的49个智能体最终会形成圆形队形,但是圆形队形最终在平面上的位置是不能指定的,该位置和智能体的初始位置的选择有关,还与智能体的通信拓扑即智能体之间的协作方式有关. 本文利用势函数方法研究了多智能体的队形控制问题,通过构造位置势函数和避撞势函数,给出了队形控制的控制策略,并证明了在该控制策略的作用下,系统能够实现期望的队形,且不会发生碰撞.最后,利用仿真说明了该方法的可行性和有效性. 图1 49个智能体的队形控制图 参考文献: [1]任德华,卢桂章.对队形控制的思考[J].控制与决策,2005, 20(6): 601-606. [2]张明,严卫生,高剑.实时位置反馈的多机器人主从式编队控制[J].火力与指挥控制,2012,37(2):12-15. [3]Wang Yintao, Yan Weisheng, Li Junbing. Passivity-based formation control of autonomous underwater vehicles [J]. IET Control Theory & Application, 2012, 6(4): 518-525. [4]Wu Yunhua, Cao Xinbin, Zheng Pengfei, et al. Variable structure-based decentralized relative attitude-coordinated control for satellite formation [J]. IEEE Aerospace and Electronic Systems Magazine, 2012, 27(12): 18-25. [5]Lafferriere G, Williams A, Caughman J, et al. Decentralized control of vehicle formations[J]. Systems and Control Letters, 2005, 54(9): 899-910. [6]郑军,颜文俊.一类分布式队形控制及其稳定性分析[J].自动化学报,2008,34(9):1107-1112. [7]Oh Kwang-kyo, Ahn Hyo-sung. Formation control of mobile agents based on distributed position estimation [J]. IEEE Transactions on Automatic Control, 2013, 58(3): 737-742. [8]郭静.仅基于相对位置或角度信息的多智能体系统队形协调控制[D].杭州:浙江大学,2011. [9]Su Housheng, Wang Xiaofan, Lin Zongli. Flocking of multi-agents with a virtual Leader [J].IEEE Transactions on Automatic Control, 2009, 54(2): 293-307. [10]Olfati-saber R.Flocking for multi-agent dynamic systems:Algorithms and theory[J].IEEE Transactions on Automatic Control, 2006, 51(3): 401-420. [11]钟守铭,刘碧森,王晓梅,等.神经网络稳定性理论[M].北京:科学出版社,2008:150-151.2 准备工作
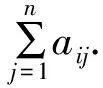
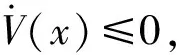
3 控制策略的设计
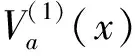
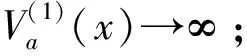
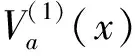
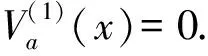
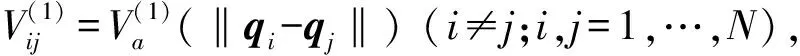
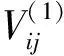
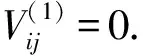
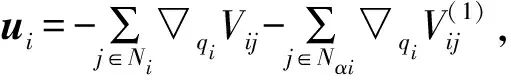
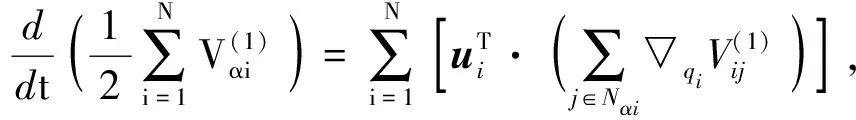
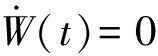
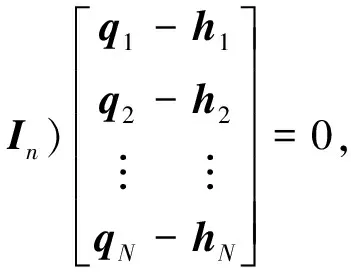
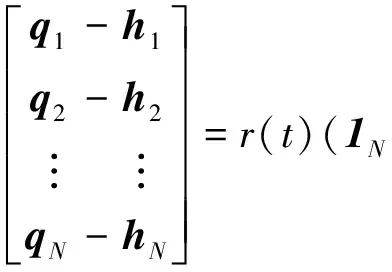
4 仿真实例
5 小 结