太赫兹波段树枝状三维各向同性左手材料设计及特性研究

王连胜，夏冬艳，汪 源，宋书建

(三亚学院理工学院，海南 三亚 572022)

左手材料是一种磁导率μ和介电常数ε在一定的电磁波频段内同时为负值的人工结构周期性材料.1968年前苏联物理学家Veselago首次从理论上提出了左手材料的概念，并指出电磁波在其中传播时会出现奇特的现象，如负折射、负切连科夫效应和反常多普勒效应等[1].之后Pendry等人的开创性工作——提出以周期排列的金属开口环谐振器 (SRR: Split-Ring Resonator) 构造等效磁导率为负值的介质的方法——引起了左手材料的研究热潮[2-3].2001年美国加州大学San Diego分校的Smith等人将SRRs和金属杆阵列 (Rods) 结合起来，首次通过实验观察负折射效应证明了左手材料的存在[4].此后反常 Doppler效应和平板透镜成像等左手材料相关效应的研究工作陆续报道[5-8]，左手材料领域已经成为新的研究热点.

太赫兹波是指频率在0.1～10 THz范围的电磁波，介于微波与红外之间.由于太赫兹的频率很高，所以其空间分辨率也很高；又由于它的脉冲很短(皮秒量级)所以具有很高的时间分辨率.同时，由于太赫兹能量很小，不会对物质产生破坏作用，所以与X射线相比更具有优势.太赫兹波的独特性能给宽带通信、雷达、电子对抗、电磁武器、天文学、医学成像、无损检测和安全检查等领域带来了深远的影响.目前左手材料的研究在微波段已经得到了一定的应用——固态天线、微型反向天线、平板聚焦透镜、带通滤波器等，光频段左手材料的研究也取得了一定的研究进展，目前太赫兹波段的左手材料的研究工作还较少[9-11]，因此研究太赫兹波段的左手材料具有极其重要的意义.本文基于微波段树枝状左手材料设计思想[12-13]，设计了太赫兹波段三维各向同性左手材料.目前制备高频段的左手材料主要有物理刻蚀方法(如聚焦离子束刻蚀)和化学制备法， 微波段左手材料可以通过在介质板上刻蚀各种金属图案来实现，而太赫兹、红外以及可见光波段主要通过化学制备法实现，本文所提出的这种太赫兹波段树枝状三维各向同性左手材料模型可通过溶剂热合成法成功的制备.太赫兹波段左手材料的实际实现将为成像技术等领域带来重大的影响.

1 太赫兹波段三维各向同性左手材料的设计

根据Zhao Xiaopeng等人的工作[12-13]，结构尺寸在毫米级的树枝状结构材料在微波段表现出磁导率和介电常数同时为负值，同时折射率也是负值.以此为基础，本文利用高频电磁仿真软件CST建立的太赫兹三维各向同性树枝状左手材料单元模型如图1所示，图1(a)为其平面效果，图1(b)为立体效果，该单元中a=20 μm，b=9 μm，c=9 μm，θ=45°，宽度和厚度为3 μm.单元结构的上下两面是理想电壁，左右两面为开放壁，其余两面为理想磁壁，这样就形成了二端矩形波导模型，利用波导法对该结构单元进行仿真，将得到的S参数反演为结构单元的折射率、等效磁导率和等效介电常数[13]，判断其左手特性.

图1 太赫兹波段三维各向同性左手材料结构单元模型示意图

2 结果与讨论

利用波导法对上述结构单元在0.1～2 THz之间的透射与反射特性进行仿真，结果如图2和图3所示，图2为该结构单元的透射与反射系数曲线，图3为透射与反射相位曲线.从结果可以看出，该结构单元在1.17～1.56 THz之间出现了一个透射峰.

为了更好的分析这种结构的谐振行为，在1.3 THz处对金属表面的感应电流进行了仿真监控，结果如图4所示.

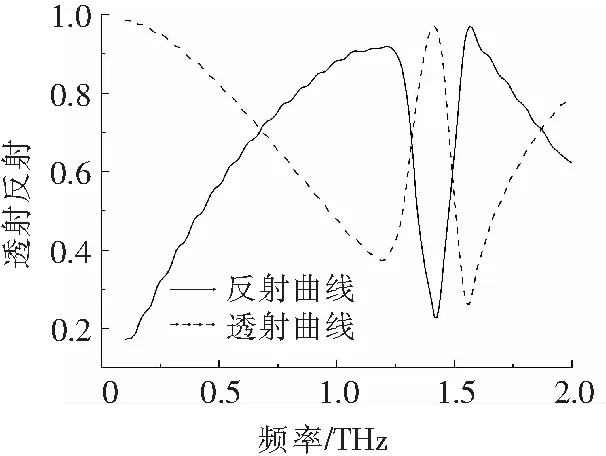
图2 透射和反射系数曲线图

图3 透射相位和反射相位曲线图

图4 1.3 THz处三维各向同性树枝状左手材料单元的表面电流分布

由图4可以看出当TEM中的磁场分量作用于结构单元后会在表面产生一致沿逆时针方向的电流元振荡，进而产生一个垂直于直面向外的磁矩M，并与原磁场方向相反，由公式M=χmH和ur=1+χm可知，当其效应足够强时，χm表现出负值，进而结构单元的磁导率表现为负值，加之由树枝两分支表面电流形成的电谐振，结构单元表现出左手透射峰.

利用上述测得的透射与反射系数及相位，根据Smith等人的理论[14]，将S参数反演为折射率和阻抗，结果如图5和图6所示，从结果可以看出该结构单元的折射率在1.17～1.38 THz之间为负值.折射率负值最大为-1.56.在此频段晶格周期与工作波长之比为1/3.2～1/2.7，满足等效媒质理论，因此所设计的模型是一个三维各向同性左手材料结构单元.

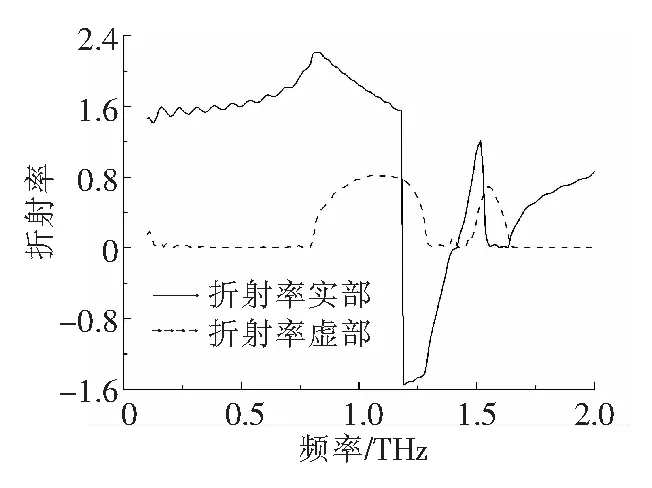
图5 折射率曲线

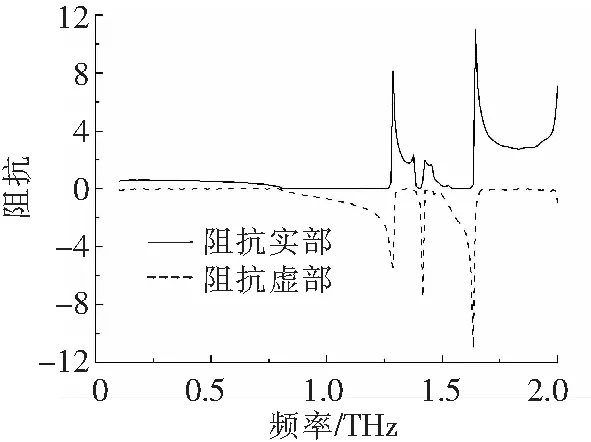
图6 阻抗曲线

利用上述计算的折射率n和阻抗z，根据ε=n/z,μ=n*z对其等效介电常数和等效磁导率进行计算，结果如图7和图8所示，从结果可以看出等效介电常数在0.82～1.38 THz之间为负值，等效磁导率在0.89～1.41 THz之间为负值.从图7、8和5看出折射率为负的频段与介电常数和磁导率为负的频段不吻合，这主要是因为：设计各向同性左手材料实现负折射率的方法是，设计各向同性材料使其介电常数ε=ε'+iε"和磁导率μ=μ'+iμ"满足不等式P=Re(ε)Im(μ)+Re(μ)Im(ε)<0，这将使得折射率实部n'<0为负值，在ε'<0和u'<0同时满足时，上述不等式成立，然而这不是必要条件，还要满足阻抗z'>0，从图6阻抗曲线可以看出0.82～1.17 THz之间阻抗z=0，显然此频段为禁带.

图7 介电常数曲线

图8 磁导率曲线

3 太赫兹波段负折射现象模拟

为了验证上述结构单元的左手特性，26°的三维各向同性树枝状左手材料楔形棱镜被用来进行负折射仿真实验，仿真模型如图9所示，单元阵列以阶梯型放置在平行于xz平面的2块金属板之间.沿y方向每放置一个单元，则沿x方向放置2个，这样形成的楔形棱镜顶角角度为26°.仿真过程中，设置平行于xoz平面的端面为理想电壁，平行于xoy平面的端面为理想磁壁，传播方向沿x轴的均匀平面波沿x轴正方向入射，均匀平面波通过楔形棱镜并与周围的均匀介质在交界处发生折射、反射，被折射和反射的电磁波在理想匹配层边界处被吸收，这样就可以通过观察电场能量在空间的分布来判断是否发生了负折射.

图9 由三维各向同性树枝状左手单元构成的26°负折射仿真实验结构图

图10给出了上述楔形棱镜在1.3 THz处的电场分布，从图中可以看出：输入波与折射波位于法线的同侧，这充分验证了上述三维各向同性树枝状左手材料单元的左手特性.

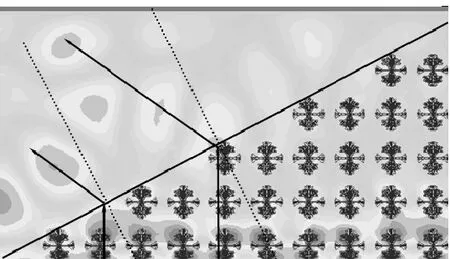
图10 由上述三维各向同性树枝状左手单元构成的26°楔形棱镜折射电场分布

4 太赫兹波段三维各向同性左手材料的缺陷效应分析

目前制备高频波段的左手材料主要有物理刻蚀方法和化学制备方法，太赫兹、红外及可见光波段的左手材料主要通过化学制备方法实现，本研究设计的太赫兹波段左手材料可以通过溶剂热合成法制备.但采用化学制备方法将会在制备过程中引入缺陷.为分析缺陷对其左手特性的影响，对图11所示的太赫兹波段三维各向同性左手材料中的①、②、③和④分支不同程度缺失的情况下其左手特性进行分析.

图11 太赫兹波段三维各向同性左手材料分支缺失示意图

本研究所设计的太赫兹波段三维各向同性左手材料在①、②、③和④分支不同程度缺失的情况下其透射和反射曲线如图12和13所示.从图中可以看出，在①分支缺失及①和②分支同时缺失的情况下，其左手透射峰依然存在，处于1.21～1.45 THz之间，频带变窄；在①、②和③分支及①、②、③和④分支同时缺失的情况下其左手透射峰消失.主要原因是：当TEM中的磁场分量作用于结构单元后会在表面产生一致沿逆时针方向的电流元振荡，进而产生一个垂直于直面向外的磁矩M，并与原磁场方向相反，由公式M=χmH和ur=1+χm可知，当其效应足够强时，χm表现出负值，进而结构单元的磁导率表现为负值，加之由树枝两分支表面电流形成的电谐振，结构单元表现出左手透射峰.当分支缺失时，在结构单元表面产生的电流元减少，进而产生的磁矩M减少，左手透射峰频带变窄，当分支缺失严重时，左手透射峰将消失.

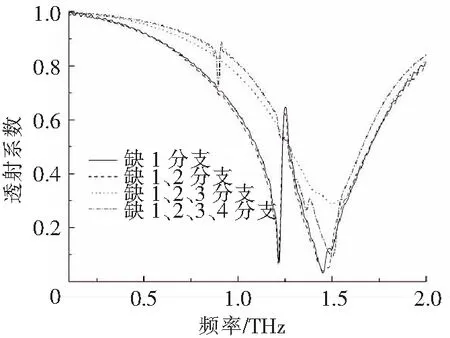
图12 不同程度分支缺失情况下的透射曲线

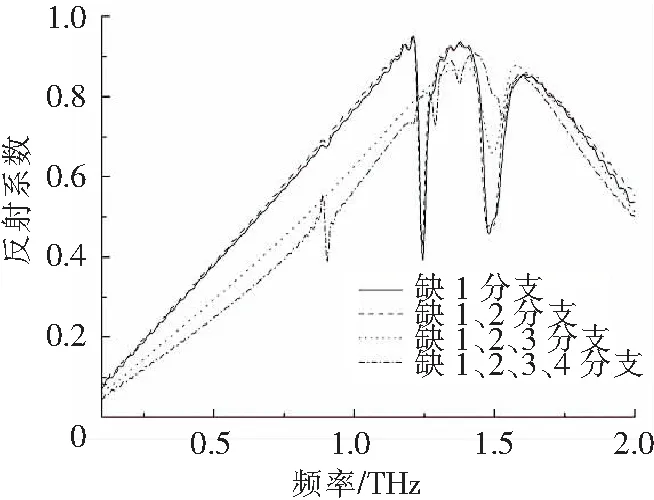
图13 不同程度分支缺失情况下的反射曲线

5 太赫兹波段三维各向同性左手材料的吸波特性

由图2可以看出，本研究所设计的太赫兹波段三维各向同性左手材料在1.3 THz处反射率为4%，因此可以通过在所设计模型的基础上，通过改进模型降低透射率以实现太赫兹波段电磁波的吸收.降低透射率较简单的方法是在电磁波入射方向上放置金属板实现.本研究用于太赫兹波段三维各向同性左手材料吸波特性分析的模型如图14所示.仿真过程中，电磁波沿z轴入射.

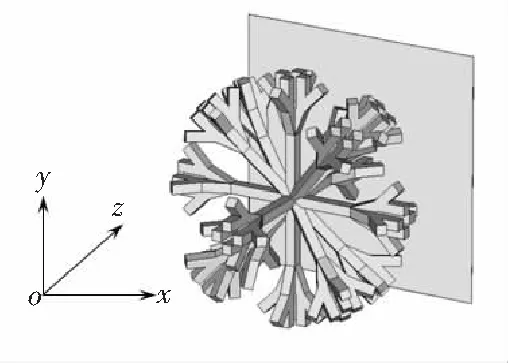
图14 吸波特性分析模型图

对图14所示的基于太赫兹波段三维各向同性左手材料的吸波体进行电磁仿真，由于采用金属底板，简化了设计，透射率T(w)=0 ，则吸收率A(w)=1-T(w)-R(w)=1-R(w)，其中R(w)为反射率，吸收率曲线如图15所示.从图15可以看出，吸波体在1.47 THz处出现了一个吸收峰，吸收率为98%.

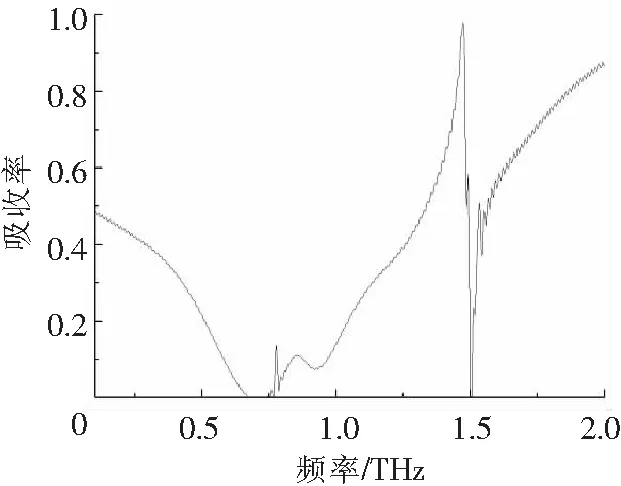
图15 基于太赫兹波段三维各向同性左手材料的吸波体吸收率曲线

6 总 结

本文以微波段树枝状左手材料为基础设计了太赫兹波段三维各向同性左手材料，结构单元具有结构简单、较容易制备等特点.模拟计算了该结构单元的有关电磁参数，折射率在1.17～1.38 THz之间表现出负值，并通过模拟负折射验证了其左手特性；通过对其缺陷效应进行分析，发现在缺陷严重情况下，其左手特性将消失；通过对模型进行改进，在1.47 THz处出现了一个吸收峰，吸收率高达98%.太赫兹波段左手材料的实际实现将为成像技术等领域带来重大的影响.

参考文献:

[1]Veselago V G. The electrodynamics of substances with simultaneously negative values of ε andμ[J]. Sov Hys Usp, 1968, 10: 509-514.

[2]Pendry J B, Holden A J， Stewart W J, et al. Extremely low frequency plasmons in metallic mesostructures[J]. Phys Rev Lett, 1996, 76:4773-4776.

[3]Pendry J B, Holden A J, Robbins D J, et al. Magnetism from conductors and enhanced nonlinear phenomena [J]. IEEE Trans Microwave Theor Techn, 1999, 47:2075-2084.

[4]Smith D R ,Padilla W J, Vier D C, et al. Composite medium with simultaneously negative permeability and permittivity[J]. Phys Rev Lett, 2000, 84:4184-4187.

[5]Seddon N, Bearpark T. Observation of the inverse doppler effect[J]. Science, 2003, 302:1537-1540.

[6]Parazzoli C G, Greegor R B, Li K, et al. Experimental verification and simulation of negative index of refraction using Snell’s law [J]. Phys Rev Lett, 2003, 90:107401.

[7]Houck A A, Brock J B, Chuang I L. Experimental observations of a left-handed material that obeys Snell's law [J]. Rhys Rev Lett, 2003, 90: 137401(1-4).

[8]Pendry J B. Negative refraction makes a perfect lens[J]. Phys Rev Lett, 2000, 85:3966-3969.

[9]Oliver P, Christian I, Benjamin R, et al. Negative index bulk metamaterial at terahertz frequencies[J].Optics Express, 2008,16(9):6736-6744 .

[10]Mohammad A, Michael N, Heinrich K.Negative-index metamaterial with polymer-embedded wire-pair structures at terahertz frequencies [J].Optics Letters, 2008, 33(22):2683-2685.

[11]Gu Jianqiang, Han Jiaguang, Lu Xinchao, et al.A close-ring pair terahertz metamaterial resonating at normal incidence [J].Optics Express, 2009,17(22): 20307-20312

[12]Zhou Xin, Fu Quanhong, Zhao Xiaopeng, et al. Negative permeability and subwavelength focusing of quasi-periodic dendritic cell metamaterials [J]. Opt Express, 2006, 14:7188-7197.

[13]Zhou Xin, Zhao Xiaopeng. Resonant condition of unitary dendritic structure with overlapping negative permittivity and permeability [J]. Appl Phys Lett, 2007, 91: 181908(1-3).

[14]Smith D R, Vier D C, Koschny Th, et al. Electromagnetic parameter retrieval from inhomogeneous metamaterials[J]. Phys Rev E, 2005, 71:036617(1-11).