饱和负荷预测中的改进Logistic算法
鲍正杰,李生虎,赵锋,陈晨,高传海
(1.合肥工业大学电气与自动化工程学院,合肥230009;2.合肥供电公司,合肥230022)
饱和负荷预测中的改进Logistic算法
鲍正杰1,李生虎1,赵锋2,陈晨2,高传海2
(1.合肥工业大学电气与自动化工程学院,合肥230009;2.合肥供电公司,合肥230022)
饱和负荷预测有助于合理规划变、配电设备容量,节约投资。针对Logistic模型依赖于饱和值的问题,提出了修正指数求解方法;针对历史负荷数据缺失问题,提出以投运距今时间为自变量,用每个投运时间对应的平均年最大负载率外推;针对预测结果随机性较大问题,采用相同投运时间的多个区域负载率均值,引入权重系数,以加重近期数据的影响,并采用实际配网数据,预测其饱和负荷。与现有方法相比,所提算法对历史负荷数据的拟合误差更小,对未来饱和负荷的预测更加可信。
饱和负荷预测;修正指数法;Logistic模型;负载率
随着工业化、城镇化进程加速,电网规模不断扩大,用电需求日益增加。在城市发展早期,负荷增长较快。一段时间后,经济趋于成熟,负荷低速缓慢增长,即负荷达到饱和。通过饱和负荷预测可以确定城市配电网的最终规模,规划变电站和线路走廊,避免出现供电能力过剩或容量得不到充分利用的问题,协调电网建设与经济发展[1-4]。负荷预测是城市电网规划的基础,饱和负荷数据是城市电网规划中确定电网最终发展规模的关键性指标,对城市电力工业的规划和发展有极为重要的指导意义。
饱和负荷预测方法主要包括外推法和空间负荷预测,前者常用Logistic曲线描述。比利时数学家Verhulst提出的Logistic曲线[5-6],最早用于生物种群的研究,通过观察研究发现,许多事物的发展过程与生物种群的发展相似,因而应用范围拓展到生物、医学及经济等领域[7-8]。对于一个确定区域的负荷增长,由于区域环境、资源、土地等因素的限制,随着地区的发展,必然会达到一个趋于饱和的状态,基于负荷生长的这种特性,可以采用Logistic曲线描述。文献[9]用Logistic模型对历史年最大负荷数据建模求得饱和负荷值;文献[10]对历史负荷数据进行趋势外推得到预测值;文献[11]对历史用电量利用生长曲线预测负荷值。上述文献都以历史负荷值作为数据,但是实际应用中长期历史数据较难取得;负荷分类往往过于笼统,不同负荷特性导致饱和预测结果不准确;单独某一区域的饱和预测结果随机性大。
Logistic函数的参数c是饱和值K的倒数。一般先求得K,将函数线性化,然后通过最小二乘法估计a和b。文献[11-12]采用了3点法、4点法、拐点法求得K值,通过非线性回归求得增长曲线;文献[13]先对生长曲线进行微分,再用差分近似替代微分求解出参数c,从而求出曲线;文献[14]提出了利用最优化理论搜索一系列c值,然后采用回归分析求得a、b,最后选出最优值。上述算法不足在于a、b的求解是建立在K基础上,K值的准确性直接影响整个模型的准确性;当a、b、c这3个参数均未知时,模型无法线性化,导致无法采用最小二乘法。在求解时,只选用其中3个或4个数据点,历史数据没有得到充分利用。
针对饱和负荷预测问题,本文改进负荷数据取值和Logistic模型求解算法。用平均年最大负载率替代年最大负荷作为数据,使不同时间点可以采用不同区域的用电数据,解决了保留的历史负荷数据时间跨度较短或缺失某些年份数据的问题。对相同年份相同类型的多个用电区域的负载率求取均值,减小了原始数据的随机性。将Logistic函数转换成修正指数曲线求解,从原始数据直接解得模型参数,充分利用历史数据,避免过度依赖饱和值K,从理论上改善了预测精度。
1 负荷数据取值方法的改进
现有饱和负荷外推预测,多是基于最大历史负荷。但是限于存储容量,配电负荷数据往往只保存较短时间,因此数据长度不足以直接外推。同时,采用历史负荷数据外推,没有考虑变、配电设备容量限制,不能直接反映供电宽松/紧张程度。
为解决上述问题,本文采用配电设备当前年份的年最大负荷量作为数据,以投运时间作为时间变量进行外推。鉴于不同配电设备容量不同,不具有外推的前提条件,因此将不同配电设备的负荷量折算到各自的额定容量。设PYmax为用电区域年最大负荷值,Pr为配电设备额定容量之和,则年最大负载率为

用负载率替代负荷值,其均值可以反映饱和负荷比例。设投运距今时间为t a的配电区域有n个,年最大负载率分别为ηt1,ηt2,…,ηtn,则距今t a的平均年最大负载率ηt为

2 Logistic模型参数的改进求解
2.1 修正指数求解法
Logistic模型有积分和微分2种形式,其中积分形式为

式中:xt为生物数或其他数量指标(如经济总量、发病数、电力负荷值等);t为时间序列;r为常数,是内禀自然增长率或瞬时增长率;K为常数,是环境负载力或容纳量;e为自然对数底;A为积分常数。
令c=1/K,a=eA/K,b=-r,则式(3)变为

令xt′=1/xt,eb=b1,则式(4)变为

而修正指数曲线的一般表达式为

式(5)具有修正指数曲线的形式,只需求得其参数,然后进行变量代换,即可得到Logistic曲线的参数。对式(5)求解得
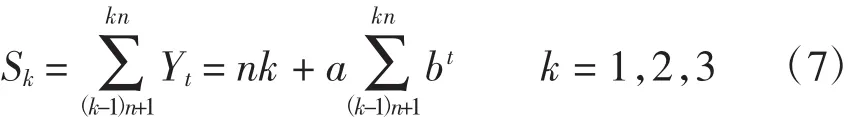
两两相减得

则

由式(7)可得

对式(9)~式(11)中求得的参数进行变量代换,得到Logistic模型的参数为

修正指数法相比现有基于有限数据点和饱和值K的现有算法,理论上提高了预测精度,解决了参数c无法确定时无法线性化求解的问题。
2.2 引入权重的修正指数法
一般来说,近期数据对预测值的影响较早期数据的影响大,因此引入加权平均数。设历史数据为η1,η2,…,η3n,共3n项,用于模型参数求解的初期、中期、近期的坐标点为M1(t1,S1),M2(t2,S2),M3(t3,S3),令权数分别为1,2,…,n,则3点的坐标(3项加权平均)分别为

即3点M1(t1,S1)、M2(t1+n,S2)、M3(t1+2n,S3)均为拟合曲线上的点,则

变量代换得Logistic曲线参数为

2.3 拟合评判指标
相对误差是绝对误差与真值的比值,表示拟合值与原始数据的接近程度。取相对误差平均值为d,其总体的可信度为

均方根误差RMSE是用来衡量观测值与真值之间的偏差,衡量拟合值与原始数据之间的差异,即

拟合优度R2是评价拟合曲线对原始数据的拟合程度,指标的值越接近1,说明拟合程度越好。

3 算例分析
以负荷细化分类中的普通住宅为例进行饱和负荷预测,首先从各配电设备采集到负荷数据,筛选出普通住宅的数据,除去其中可信度不高的数据点,选取其中的面积接近、负荷特性尽可能一致的普通住宅进行负荷分析;然后将普通住宅的负荷数据按投运的年份分类,分别求得每个投运年份的配电设备的平均年最大负载率。各投运年份的数据点数目主要由采集到的该投运年份的数据点个数决定。各投运年份的数据点数目及年最大负载率均值如表1所示。

表1 普通住宅历史负荷数据Tab.1Historical load date of residence
基于负载率的饱和负荷预测不能处理未来新增设备容量问题,直接采用负荷数据外推即可。
针对负荷值和负载率进行饱和负荷预测各有其适用范围。前者将年最大负荷值进行趋势外推能够对一个地区负荷增长状况有所了解,了解其最终达到的饱和值,但预测结果只对某一用电负荷,不具有普适性;用年最大负载率进行预测可以在预测过程中采用多个用电负荷数据的均值,减小随机性,也能够为今后同类配电设备容量的选择提供借鉴。同时,采用平均年最大负载率预测,每个投运年份有多个数据点,可以删去其中有新增设备容量的数据点。
4点法是目前Logistic参数估计中较为成熟的方法,国内外都得到了较广泛的应用,取得了较好的效果,计算也较为简便[10~12]。分别采用本文提出的修正指数法和引入权重修正指数法计算饱和时达到的负载率,并与4点法的计算结果进行比较。
1)4点法
4点法采用的数据为(1,24.41)、(4,34.34)、(6,37.80)、(9,47.01),则求解参数K的公式为

求解得K=65.931 6,c=1/K=0.015 17。利用最小二乘拟合得到参数a、b的值:a=0.029 8,b= -0.173 8。则拟合Logistic曲线为

2)改进求解法
修正指数求解法求得的Logistic曲线为

引入权重的修正指数法求得的Logistic曲线为

上述3种参数求解方法的拟合结果如表2所示。

表23 种求解方法的拟合数据Tab.2Fitting data of three methods %
以相对误差平均值d、均方根误差RMSE、拟合优度R2为评判指标,比较3种方法得到的参数的准确性,评价结果如表3所示。

表3 数据拟合指标比较Tab.3Comparison of data fitting indices
由表3可知,4点法的相对误差平均值d相对较差,引入权重后相对误差均值减小;引入权重的修正指数法其均方根误差RMSE指标最差,修正指数法拟合效果最好;引入权重的修正指数法的拟合优度R2指标较差,修正指数法更接近于1,效果更好。
3种方法的饱和预测结果见图1,饱和值分别为65.92、76.20、104.75,即按目前的配电设备配置原则进行配置,负荷饱和时负荷值为配电设备容量的65.92%、76.20%、104.75%。

图1 饱和负荷预测结果Fig.1Results of saturated load forecast
由图1可知,4点法和修正指数求解法结果较为接近,引入权重的修正指数法预测值大于前两者,这是由于引入权重后加强了近期值对预测结果的影响,而负荷的发展趋势基本是增长趋势,因而引入权重后预测结果较大。但4点法仅采用了4个数据点随机性较大,选择的数据点不同会出现较大差异,建议将修正指数求解法作为低方案预测结果,而引入权重的修正指数法比修正指数法更不保守,预测结果与当前用电量处于快速增长阶段的实际情况更为接近,可作为高方案应用。
负荷预测结果检验分为2个方面,即数学收敛性和工程有效性。本文所提指标,量化了饱和负荷预测模型拟合历史数据的误差,反映了数学收敛性。但数学收敛是负荷结果真实的必要而非充分条件。
通过负荷调查可以掌握饱和负荷的真值,统计用电区域达到饱和时的用电负荷类型、数目、同时率进行计算。利用饱和负荷真值即可检验预测的准确性。只是负荷调查工作量大,偏于工程应用。若只调查单个区域,饱和负荷预测结果不具有普遍意义。
4 结论
(1)针对饱和负荷预测中保留的负荷数据时间跨度较短,以投运距今时间为时间变量,用每个投运时间对应的平均年最大负载率趋势外推,能够较好地解决历史数据缺失的问题;外推得到的负荷趋于饱和时负载率能够给同类用电负荷配置合理的配电容量提供借鉴;且通过对数据进行平均减少随机性。
(2)修正指数求解法和引入权重的修正指数法充分利用了所有历史负荷数据,提高了预测结果可信度,并解决了饱和参数无法确定时,模型无法线性化求解的问题。
(3)引入权重的修正指数法预测值大于修正指数法,但后者较前者保守。在应用时综合考虑两种求解法的预测结果,可将预测结果分别作为低方案和高方案;也可采用组合预测法,根据实际情况灵活确定两种预测结果的权重系数,使之达到良好的预测效果。
[1]崔凯,李敬如,刘海波,等(Cui Kai,Li Jingru,Liu Haibo,et al).城市负荷饱和阶段电力规划方法及其在济南电网中的应用(City′s power planning methods at the stage of load saturation and its application in Jinan power grid)[J].电网技术(Power System Technology),2007,31(S2):131-134.
[2]崔凯,李敬如,赵彪,等(Cui Kai,Li Jingru,Zhao Biao,et al).城市饱和负荷及其预测方法研究(Research on city saturated load and its forecast methods)[J].电力技术经济(Electric Power Technologic Economics),2008,20(6):34-38.
[3]黄银华,彭建春,李常春,等(Huang Yinhua,Peng Jianchun,Li Changchun,et al).马尔科夫理论在中长期负荷预测中的应用(Application of Markov theory in mid-long term load forecasting)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2011,23(5):131-136.
[4]顾洁(Gu Jie).电力系统中长期负荷的可变权综合预测模型(Study on the varied weight synthesis model of midlong term load forecasting in power system)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2003,15(6):56-60.
[5]卫志农,滕俊,王丹,等(Wei Zhinong,Teng Jun,Wang Dan,et al).电力系统年最大负荷概率预测(Probabilistic forecasting for annual peak load of power systems)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2004,16(6):64-67.
[6]肖峻,杜柏均,耿芳(Xiao Jun,Du Bojun,Geng Fang).城市电力负荷饱和分析方法(A method for city power load saturated analyzing)[J].电力科学与技术学报(Journal of Electric Science and Technology),2009,24(4):54-58.
[7]Yang K.Basic properties of mathematical population models[J].Journal of Biomathematics,2002,17(2):129-142.
[8]黄如宝,李斌(Huang Rubao,Li Bin).固定资产投资预测的Logistic模型及实证分析(Logistic model and positive research for investment in fixed assets)[J].同济大学学报(JournalofTongjiUniversity),2005,33(2):251-254.
[9]Fu C W,Nguyen T T.Models for long-term energy forecasting[C]//IEEE Power Engineering Society General Meeting.Toronto,Canada:2003.
[10]Jia Yudong,Li Shenghu,Tan Yun,et al.Improved parametric estimation of logistic model for saturated load forecast[C]//IEEE Power and Energy Engineering Conference. Shanghai,China:2012.
[11]王吉全,赵玉林(Wang Jiquan,Zhao Yulin).生长曲线在电力负荷预测中的应用(Application of logistic curve in electric power load forecast)[J].电网技术(Power System Technology),2004,28(22):36-39.
[12]殷祚云(Yin Zuoyun).Logistic曲线拟合方法研究(Study on the fitting methods of logistic curve)[J].数理统计与管理(Application Statistics and Management),2002,21(1):41-46.
[13]王福林(Wang Fulin).一种生长曲线的参数估计方法(A method for estimating the parameters of logistic curve)[J].生物数学学报(Journal of Biomathematics),1997,12(5):398-402.
[14]王福林,王吉权(Wang Fulin,Wang Jiquan).生长曲线参数估计的一种新方法—优化回归组合法(An improved method for estimating the parameters of logistic curve—optimization regression combing method)[J].生物数学学报(Journal of Biomathematics),2007,22(3):533-538.
Improved Logistic Model for Saturated Load Forecast
BAO Zheng-jie1,LI Sheng-hu1,ZHAO Feng2,CHEN Chen2,GAO Chuan-hai2
(1.School of Electrical Engineering and Its Automation,Hefei University of Technology,Hefei 230009,China;2.Hefei Electric Power Company,Hefei 230022,China)
The saturated load forecast benefits to plan capacity of transmission and distribution equipments,and to optimize investment.The amended solution to the exponential function is proposed to avoid dependency of Logistic model on the saturated value.By treating the installment year as independent variable,the saturated load is extrapolated via the annual maximum loading rate,avoiding the problem of insufficient load data.Randomness of load forecast is decreased by utilizing average loading rate of multiple areas with the same installation year.The weighting coefficient is proposed to augment contribution of recent load data.The proposed algorithm is applied to forecast the saturated load of the practical distribution system,which yields less fitting error to the historical load data,and more trustworthy results to the saturated load compared with the existing methods.
saturated load forecast;amended exponential method;Logistic model;load rate
TM714
A
1003-8930(2014)11-0007-05
鲍正杰(1990—),男,硕士研究生,研究方向为交直流系统运行与控制。Email:bzj15403@163.com
2012-12-27;
2013-05-18
国家自然科学基金项目(51277049)
李生虎(1974—),男,博士,教授,博士生导师,研究方向为电力系统可靠性、风电系统稳定性、柔性输电技术。Email:shenghuli@hfut.edu.cn
赵锋(1985—),男,硕士,工程师,研究方向为城市电网规划。Email:zhaofeng0522@163.com

