一种用于陀螺随机漂移预测的多尺度混合建模方法

何 星，王宏力，陆敬辉，姜 伟

（第二炮兵工程大学 控制工程系，西安 710025）

一种用于陀螺随机漂移预测的多尺度混合建模方法

何 星，王宏力，陆敬辉，姜 伟

（第二炮兵工程大学 控制工程系，西安 710025）

针对陀螺随机漂移时间序列由于非平稳和非线性造成单一预测模型难以准确跟踪其变化趋势的问题，提出了一种基于集合经验模态分解(EEMD)和灰色极端学习机(GELM)的多尺度混合建模方法。首先，利用集合经验模态分解将随机漂移时间序列按照频率高低分解为多个本征模式分量和一个余量；然后针对不同类型时频特性分量选择合适激活函数和隐层神经元数目的GELM分别进行预测；最后，以等权相加的方式得到最终预测结果。将该方法用于某型激光陀螺随机漂移预测中，仿真结果表明：混合预测模型能够准确预测陀螺随机漂移，预测精度比残差GM（1,1）和GELM预测模型分别提高了33.43%和23.47%，可为激光陀螺的漂移补偿、故障预报和可靠性诊断提供依据。

集合经验模态分解；多尺度混合建模；灰色极端学习机；随机漂移；预测

激光陀螺作为一种基于萨格奈克效应光学传感器，具有精度高、测量范围宽、内部没有活动部件、受力学环境影响小、寿命长等特点，是捷联惯导系统的理想测量器件，因而得到了广泛的应用，也引起可众多学者进行相关研究[1,2]。然而，由于激光陀螺内部多种噪声源以及外部环境干扰的影响，造成了使用过程中的随机误差，严重影响激光陀螺的性能，加之随机漂移由量化噪声、角度随机游走、零偏不稳定性及角速率随机游走等各种随机干扰因素引起，无法用确定的函数关系描述，因此，建立合理正确的误差模型，预测随机漂移的变化趋势，对于提高导弹控制系统的精度十分重要[3]。

激光陀螺随机漂移时间序列的最大特点是具有随机性和非线性，单一的预测模型很难准确对其进行预测。经验模式分解(EMD)是一种解决非线性和非平稳信号的时频分析方法，可从复杂的信号中直接分离出从高频到低频的若干基本信号，即本征模式分量(IMF)，从而获取更多有用信息[4]。但EMD由于信号的间歇性导致模态混叠，不仅使得时频分布混乱，而且造成无法解释每个IMF代表的准确含义，为解决模态混叠问题，Huang等人提出了一种集合经验模式分解(EEMD)[5]方法。EEMD利用高斯白噪声在整个时频空间均匀分布的特性，通过在每次EMD中添加不同幅度的高斯白噪声来消除模态混叠，相比EMD取得了更好的效果，已成功应用于信号处理和机械故障诊断等领域[6-10]。

本文针对陀螺随机漂移预测问题，提出一种EEMD方法与灰色极端学习机（GELM）方法相结合的多尺度混合预测模型，该模型融合了EEMD与GELM二者在处理非平稳非线性时间序列中的优势，根据频率高低分别建模，能够充分利用漂移信号自身信息训练模型，从而获得比传统单一预测模型更高的预测精度。

1 集合经验模态分解(EEMD)

EEMD是一种噪声辅助数据分析方法，它利用了高斯白噪声具有频率均匀分布的统计特性。当加入高斯白噪声后，信号将在不同尺度上具有连续性，这样可以促进抗混分解，有效解决了EMD方法产生的模态混叠现象。其算法步骤如下[7]：

① 初始化EMD运行总次数M，加入白噪声的幅值，并令m=1。

② 对带有白噪声的信号执行第m次EMD分解。

(a) 在目标信号上加入给定幅值的白噪声：

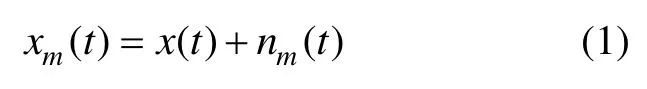
式中，nm(t)表示第m次加入的白噪声，xm(t)表示第m次分解时的加噪信号。

(b) 利用EMD分解得到加噪信号xm(t)的I个IMF分量ci,m(i=1,2,…,I)，ci,m为第m次分解得到的第i个IMF分量，I为第m次分解得到的IMF分量总数。

(c) 如果m＜M，变m为m+1，反复执行步骤(a)～(b)，但是每次加入不同的白噪声序列。

③ 计算M次分解得到的对应IMF的均值：

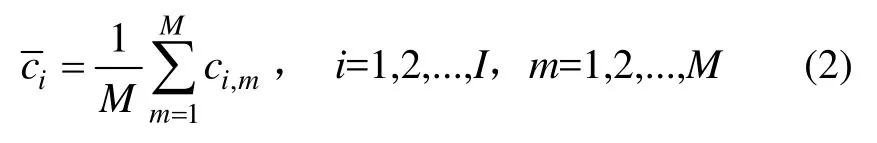
2 灰色极端学习机（GELM）

2.1 极端学习机回归原理

极端学习机（ELM）是2006年Huang等提出的一种新颖的单隐层前馈神经网络学习算法[8]，相比传统的BP神经网络、RBF神经网络，它将参数训练的迭代调整过程转化为求解线性方程组，解析求得具有最小范数得最小二乘解作为网络权值，整个训练过程可一次完成无需迭代，这使得ELM的训练速度获得了显著提升，已在模式识别与回归估计等问题中得到了成功应用[9-11]。ELM的回归原理可归纳为：

给定N个训练样本，其中输入样本，输出样本ti=，具有N～个隐藏节点和激活函数为的SLFNs输出为：

式(4)中的N个方程可以简写为：

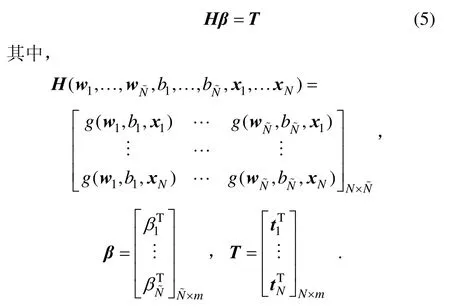
H称为神经网络的隐层输出矩阵，H的第j列表示第j个隐层节点关于的输出矩阵。

最终得到训练后的ELM回归模型为：

从上述ELM回归原理可以看出，利用ELM进行回归预测仅需要计算其输出权值β即可，其神经元参数可在指定区间内随机生成，因此大大节省了训练时间。

2.2 灰色极端学习机的实现步骤

由于灰色预测在“贫信息”、“小样本”样本处理上的优异性能，已被成功用于故障预测领域[16,17]。但是由于激光陀螺随机漂移数据的随机性和非线性等特点，使得直接利用GM（1,1）模型进行预测会产生很大的误差，无法准确跟踪随机漂移的变化趋势，因此必须采用合适方法对灰色预测结果进行误差补偿，结合前述极端学习机的诸多优点，本文利用其对灰色预测结果进一步进行误差补偿。GELM的预测步骤为：

① 对随机漂移数据进行 GM（1,1）预测，得到初步预测序列Y'；

② 利用预测值与真实值求取预测残差序列e；

③ 选择合适隐层神经元数目，利用ELM建立残差序列预测模型，得到残差预测序列e'；

④ 根据Y=Y'+e'得到最终随机漂移预测结果。

3 EEMD-GELM混合预测模型在激光陀螺随机漂移预测中的应用

3.1 混合预测模型

基于 EEMD方法对于复杂信号良好的分解能力以及ELM由于传统神经网络的训练速度和泛化性能，EEMD-GELM混合模型充分利用二者的优势，能够有效改善目前采用原始漂移序列直接进行建模引起预测结果不准确的缺陷。EEMD-ELM混合预测模型流程框图如图1所示。

预测步骤为：

① 对原始激光陀螺随机漂移序列进行EEMD分解，得到不同频率的本征模式分量；

② 通过分析各本征模式分量的时频特性，选择不同的激活函数和隐层节点数目进行 GELM预测；

③ 将各分量预测结果进行等权求和，获取最终预测结果。

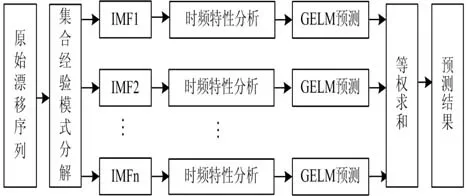
图1 混合预测模型结构框图Fig.1 Block chart of hybrid prediction model

3.2 仿真验证

激光陀螺的漂移误差包括静态漂移误差、动态漂移误差以及随机漂移误差。静态漂移误差以及动态漂移误差是分别与导弹线运动和角运动相关的确定性误差项，可通过分析或者实验标定建立相应的模型予以补偿，因此，激光陀螺随机漂移成为激光捷联惯导系统的主要误差源之一，而利用激光陀螺随机漂移历史数据建立时间序列预测模型对其进行补偿是主要手段之一。

为获取预测样本数据，将精密测试转台安装在独立的地基上，且转台的转轴与当地低垂线平行，然后将某型激光陀螺仪通过夹具安装在工作台上面，其敏感轴与转台转轴平行。当测试转台工作处于静止状态，每天启动陀螺仪进入稳定工作状态后，以1 Hz采样频率连续采样2 h，持续采集42 d，通过计算获得该激光陀螺仪的42个逐日漂移数据。以这42个逐日漂移数据作为样本数据，首先，利用EEMD对随机漂移数据进行分解，得到4个本征模式分量IMF1～IMF4以及余项r4，分解结果如图2所示。为便于分析和比较，分别采用本文方法、残差GM（1,1）以及GELM模型分别对随机漂移序列进行预测。嵌入维设为 6，即用前6个数据预测第7个数据，滚动生成36组样本，选取前29组数据作为训练样本，其余7个作为测试样本用来检验预测效果。由于激活函数和隐层神经元个数的选择对极端学习机的泛化性能影响很大，因此针对不同信号时频特性选择适合的激活函数以及最佳隐层神经元数目对预测结果十分重要。RBF函数是一种典型的局部自适应函数，具有较好的局部自适应能力，通过调整函数宽度，能够很好地模拟出局部相关性强、波动较大的信号；sigmoid函数是一种典型的全局性函数，能够使得神经元有很大的输入可见区域，适用于变化平缓的平稳信号建模。

图2 激光陀螺随机漂移时间序列EEMD结果Fig.2 EEMD result of laser gyro random drift sequence

针对本文多尺度混合建模方法：由于高频分量IMF1和IMF2波动性较大且存在一定随机成分，因此选择RBF函数作为激活函数；IMF3、IMF4和r4均为低频分量且表现出明显的周期和趋势变化规律，因此选择sigmoid函数作为激活函数；对于单一GELM直接预测方法，由于漂移时间序列包含多种复杂成分，因此选择RBF函数作为激活函数建立预测模型。对于隐层神经元数目，选择留一法（Leave-one-out,LOO）交叉验证确定。

图3为利用灰色极端学习机对陀螺漂移时间序列分解得到的4个本征模式分量和1个余量的预测结果，可以看出，预测结果与实测值基本吻合，尤其对于变化较缓慢的IMF3、IMF4和r4预测值与实测值误差很小。

将各分量预测结果等权相加即可得到陀螺漂移时间序列的最终预测结果，此外，利用灰色极端学习机直接进行预测也可得到陀螺漂移时间序列预测结果，如图4所示和表1所示。可以看出，利用本文所提出的 EEMD-GELM混合预测模型的预测结果和原始残差补偿GM(1,1)以及GELM预测模型相比，平均相对误差分别为3.58%、6.76%和5.88%，EEMD-ELM混合预测模型的预测精度明显高于另两种预测模型，均方根误差结果显示出同样的结论。这是由于陀螺随机漂移是一个复杂的非线性信号，直接对其建模预测精度往往很差，而经过对漂移时间序列进行集合经验模式分解，得到多个具有一定规律的信号分量，对各分量建立准确的预测模型相对容易，因此，EEMD-ELM混合预测模型能够实现对陀螺随机漂移时间序列更准确的预测。

图3 漂移时间序列各分量预测结果Fig.3 Prediction results for each part of drift time series

图4 三种方法预测结果曲线Fig.4 Prediction result curves of three methods

表1 两种方法的预测误差结果Tab.1 Prediction error results of two methods

4 结 论

陀螺随机漂移时间序列是一种典型非线性和非平稳时间序列，如果仅利用单一预测模型很难准确跟踪其变化趋势。本文提出一种EEMD分解与灰色极端学习机集成的混合预测模型，并将其运用于陀螺随机漂移预测。该模型首先通过EEMD分解将变化规律异常复杂的陀螺漂移时间序列按其内在特性自适应地分解为多个变化规律明显的本征模式分量和一个余项，然后通过分析各分量时频特性，选择合适的激活函数和隐层神经元数目，利用灰色极端学习机分别对这些分量进行预测，最后以等权求和的方式得出漂移时间序列的预测结果。将本文方法应用于某型激光陀螺逐日漂移时间序列预测中，仿真结果表明混合模型能够取得了比单一模型更好的预测效果，可为陀螺随机漂移补偿、故障预报和可靠性诊断提供可靠依据。

[1]YU Hua-peng,WU Wen-qi,WU Mei-ping,et al.Systematic angle random walk estimation of the constant rate biased ring laser gyro[J].Sensors,2013,13(3): 2750- 2762.

[2]吴赛成，秦石乔，王省书，等.激光陀螺惯性测量单元系统级标定方法[J].中国惯性技术学报，2011，19(2)：185-189.WU Sai-cheng,QIN Shi-qiao,WANG Xing-shu,et al.Systematic calibration method for RLG inertial measurement unit[J].Journal of Chinese Inertial Technology,2011,19(2): 185-189.

[3]张启鸿，王跃鹏，邓志红，等.激光陀螺漂移数据建模及分析[J].中国惯性技术学报，2006，14 (3)：42-46.ZHANG Qi-hong,WANG Yue-peng,DENG Zhi-hong,et al.Modeling and analysis of laser gyro drift data[J].Journal of Chinese Inertial Technology,2006,14(3): 42-46.

[4]HUANG Norden E,SHEN Zheng,LONG Steven R.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[C]//Royal Society of London Proceedings Series A,1998,Vol.454: 903-995.

[5]WU Zhao-hua,HUANG Norden E.Ensemble empirical mode decomposition: A noise-assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1): 1-41.

[6]陈略，唐歌实，訾艳阳，等.自适应EEMD 方法在心电信号处理中的应用[J].数据采集与处理，2011，26(3)：361-366.CHEN Lue,TANG Ge-shi,ZI Yan-yang,et al.Appl ication of adaptive ensemble empirical mode decomposition method to electrocardiogram signal processing[J].Journal of Data Acquisition & Processing,2011,26(3):361-366.

[7]LEI Ya-guo,HE Zheng-jia,ZI Yan-yang.Application of the EEMD method to rotor fault diagnosis of rotating machinery[J].Mechanical Systems and Signal Processing.2009,23: 1327-1338.

[8]JIANG Hong-kai,LI Cheng-liang,LI Hua-xing.An improved EEMD with multiwavelet packet for rotating machinery multi-fault diagnosis[J].Mechanical Systems and Signal Processing,2013,36(2): 225-239.

[9]Amirat Y,Choqueuse V,Benbouzid M.EEMD-based wind turbine bearing failure detection using the generator stator current homopolar component[J].Mechanical Systems and Signal Processing,2013,41(1-2): 667-678.

[10]WANG Xia,LIU Chang-wen,BI Feng-rong,et al.Fault diagnosis of diesel engine based on adaptive wavelet packets and EEMD-fractal dimension[J].Mechanical Systems and Signal Processing,2013,41(1-2): 581-597.

[11]HUANG Guang-bin,ZHU Qi-yu,SIEW Chee-Kheong.Extreme learning machine: Theory and applications[J].Neurocomputing,2006,70: 489-501.

[12]Lan Y,Soh C Y,Huang G B.Constructive hidden nodes selection of extreme learning machine for regression[J].Neurocomputing,2010,73(16/17/18): 3191-3199.

[13]何星，王宏力，陆敬辉，等.灰色稀疏极端学习机在激光陀螺随机误差系数预测中的应用[J].红外与激光工程，2012，41(12)：3305-3310.HE Xing,WANG Hong-li,LU Jing-hui,et al.Application of grey sparse ELM in laser gyro random error coefficient prediction[J].Infrared and Laser Engineering,2012,41(12): 3305-3310.

[14]HUANG Guang-bin,ZHOU Hong-ming,et al.Extreme learning machine for regression and multiclass classification[J].IEEE Trans on Systems,Man,and Cybernetics-part B:Cybernetics,2012,42(2): 513-529.

[15]Shrivastava N A,Panigrahi B K.A hybrid wavelet-ELM based short term price forecasting for electricity markets[J].Electrical Power and Energy Systems,2014,55: 41-50.

[16]白俊卿，张科，卫育新.光纤陀螺随机漂移建模与分析[J].中国惯性技术学报，2012，20(5)：621-624.BAI Jun-qing,ZHANG Ke,WEI Yu-xin.Modeling and analysis of fiber optic gyroscope random drifts[J].Journal of Chinese Inertial Technology,2012,20(5): 621-624.

A multi-scale modeling method using for gyro random drift prediction

HE Xing,WANG Hong-li,LU Jing-hui,JIANG Wei
(Department of Control Engineering,The Second Artillery Engineering University,Xi’an 710025,China)

In view that the time series of gyro random drift can not be precisely predicted by single forecasting model due to its non-linear and non-stationary characteristics,this paper proposes a hybrid multi-scale modeling method based on ensemble empirical mode decomposition (EEMD) and grey extreme learning machine(GELM).Firstly,the drift error data is decomposed into a series of intrinsic mode function and one residue via EEMD; Secondly,GELM predicting models with appropriate activation functions and hidden nodes are constructed to predict each intrinsic mode function and residue respectively; In the end,the outputs of each predicting model are added with equal weight to obtain the final prediction result.By using the proposed method for a laser gyro random drift prediction,the experiment is made which shows that the hybrid prediction method can get more precise result than remanet GM(1,1) and GELM prediction models,whose prediction accuracy increases 33.43% and 23.47% respectively.The hybrid model could provide reliable evidence for drift compensation,fault prediction and reliability diagnoses of laser gyro.

ensemble empirical mode decomposition; multi-scale mixed modeling; grey extreme learning machine; laser gyro random drift; prediction

TP391

：A

1005-6734(2014)02-0271-05

10.13695/j.cnki.12-1222/o3.2014.02.024

2013-10-23；

：2014-01-20

国家自然科学基金项目(61004128)

何星（1985—），男，博士研究生，主要研究方向为智能故障诊断。E-mail：trees241@163.com.

联 系 人：王宏力（1965—），男，教授，博士生导师，主要研究方向为智能故障诊断、测试性分析与评估。