光纤陀螺信号的解耦自适应Kalman滤波降噪方法

李 杨，胡柏青，覃方君，查 峰

（海军工程大学 电气工程学院，武汉 430033）

光纤陀螺信号的解耦自适应Kalman滤波降噪方法

李 杨，胡柏青，覃方君，查 峰

（海军工程大学 电气工程学院，武汉 430033）

针对光纤陀螺（FOG）输出信号的随机噪声问题，提出了一种解耦自适应Kalman滤波方法用于FOG信号降噪。方法采用Allan方差分析法估计量测噪声的方差参数，Kalman滤波过程与量测噪声方差的估计过程完全独立，避免了 Kalman滤波器与量测噪声估值器间的相互耦合。利用时间序列分析法对 FOG的随机噪声进行建模，并在建立的二阶自回归模型的基础上，采用本文滤波方法对采集的 FOG实测数据随机噪声进行了试验验证。与传统方法相比，提出的滤波方法具有更好的降噪效果，噪声均方误差降低40%以上。

光纤陀螺；ARMA模型；Allan方差；解耦；自适应滤波

光纤陀螺（fiber optic gyroscope，FOG）是基于Sagnac效应测量载体角速度变化的敏感元件，具有抗冲击、成本低、频带宽、可靠性高等优点，因而在惯导系统中有着广泛的应用前景[1-2]。由于材料、加工工艺等条件限制，目前市场上大部分FOG都属于中低精度，难以满足惯导系统对高精度陀螺的需求。通过对陀螺随机噪声进行建模补偿，是进一步提高FOG精度的重要途径。

FOG性能主要受常值漂移及随机漂移的影响[2]，其中常值漂移影响FOG的长期性能，可以通过漂移补偿计算消除。随机漂移是一种宽带噪声，可以描述为一阶马尔科夫过程，是影响惯导系统性能的主要因素之一。为抑制FOG的随机噪声，通常采用FOG的随机漂移模型及卡尔曼滤波方法对 FOG的输出数据进行递推式滤波。但在实际应用中很难得到精确的噪声模型和噪声统计特性，采用标准卡尔曼滤波会产生滤波发散现象。为解决此问题，通常采用自适应滤波技术[3]，在滤波的同时利用观测信息不断估计和修正模型参数以提高滤波精度。Sage和Husa提出了一种自适应滤波算法[4]，可在线计算系统噪声协方差阵Q和量测噪声协方差阵R。但 Sage-husa自适应滤波中Kalman滤波公式推导与噪声参数的估计是直接在时域上进行的，相互之间具有内在联系性和较强的耦合性，因而容易造成滤波器的不稳定。本文提出了一种解耦自适应Kalman滤波方法，该方法通过Allan方差分析法估计量测噪声的方差参数，量测噪声方差的估计过程与 Kalman滤波过程完全独立，因而能降低滤波发散的风险，有效抑制FOG随机噪声。

1 时间序列分析法建模

时间序列分析是对一组有序的随机数据进行分析和研究的现代统计分析方法[5]，该方法将现在时刻的状态用过去时刻的状态表示，进而预测系统未来的状态。时间序列分析法的基本模型是自回归滑动平均（auto regression moving average，ARMA）模型，ARMA(p,q)模型可表示为：

式中，y(t)为随机信号时间序列，ε(t)为白噪声序列，，p q、为模型阶次，ai、ci为模型系数，为延迟算子。

实验室目前拥有1个F120H型光纤陀螺和2个F98H光纤陀螺仪如图1所示，其零偏稳定性指标分别为0.02 (°)/h、0.04 (°)/h。

图1 实验室F120H型光纤陀螺仪Fig.1 Laboratory F120H FOG

在实验室条件下，将F120H型FOG水平安装在双轴速率转台如图2所示，得到一组FOG静态原始输出数据如图3所示。

图2 实验室高精度双轴速率转台Fig.2 Laboratory biaxial rate turntable with high precision

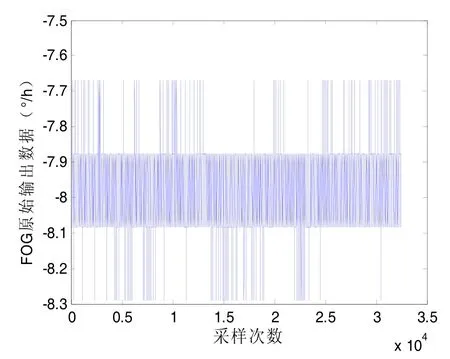
图3 FOG原始输出数据(100 Hz)Fig.3 The raw output data of FOG (100 Hz)

FOG随机噪声是一个非平稳随机过程，对该随机噪声数据构成的随机噪声序列进行平稳化处理之后，分别采用一、二阶自回归模型AR(1)、AR(2)来描述。采用递推最小二乘算法[6]可对拟定的AR(1)、AR(2)模型参数进行估计，估计结果如表1所示。

表1 各模型拟合参数及残差Tab.1 Fitting parameters and residual error of each model

对比模型残差值可看出 AR(2)模型的精度更能够反映FOG随机噪声特性。本文对FOG随机噪声建立AR(2)模型，即：

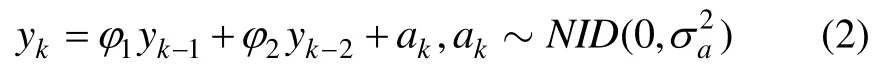
式中，yk为AR(2)模型的输出，ak为零均值，方差为的白噪声；NID中，N表示当k固定时，ak是正态分布的随机变量；ID表示当k变动时，｛ak｝之间是彼此独立。

采用递推最小二乘算法估计模型参数，得到AR(2)模型为：

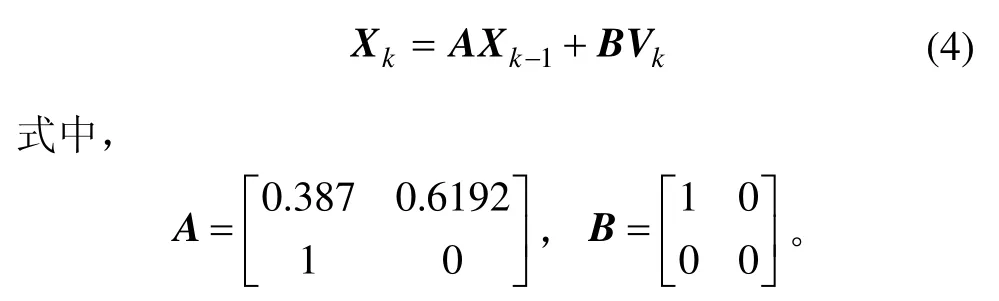
设Wk为 AR(2)模型的估计误差，则有，设系统输出为：Zk=Yk，则构建系统量测方程为：

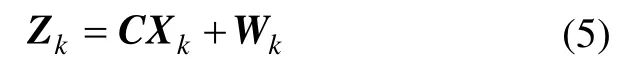
式中，C=[1 0]，Vk、Wk的统计特性为：

在实际应用中，FOG随机噪声的统计特性难以准确获得，时间序列分析建模参数具有对随机噪声的敏感性和不稳定性，当 FOG随机噪声数据离线所建的AR(2)时序模型出现偏差时，需要进行滤波方程模型和随机噪声统计量的补偿，因此考虑采用自适应滤波方法进行滤波补偿。

2 解耦自适应Kalman滤波方法

Kalman滤波是一种递推线性最小方差估计，根据得到的FOG随机噪声AR(2)模型，利用Kalman滤波技术可以对陀螺随机噪声进行最优估计。但由于FOG随机噪声统计特性难以准确获得，此时标准 Kalman滤波的滤波精度会降低，甚至可能发散。为此，在对Allan方差和Sage-husa自适应滤波研究的基础上，本文提出了一种采用 Allan方差进行量测噪声方差估计的解耦自适应Kalman滤波方法。

2.1 Allan方差理论

Allan方差法[6]是20世纪60年代由美国国家标准局的David Allan提出的，它是一种基于时域的分析方法，可广泛应用于任何精密测量仪器。Allan方差法的主要特点是能够非常容易地对各种误差源及其噪声统计特性的贡献进行细致的表征和辨识。

现以光纤陀螺的角速率输出为采样数据，简单阐述Allan方差的定义与计算过程。首先以采样间隔0τ对光纤陀螺的输出角速率进行采样，采样长度为N。将采集的N个数据分成K组，每组包含个采样点。

在实际陀螺测试中，数据长度和分组数决定了Allan方差的估计精度。

上述 Allan方差的定义基于的测量值为光纤陀螺的角速率信息。光纤陀螺输出为角增量θ(t)，则增量的测量值是在采样时刻上进行的，记为。tk和tk+τ时刻间的平均角速率为：

2.2 量测噪声方差的解耦估计

Sage和Husa提出了一种自适应滤波算法，可在线计算系统噪声方差阵Q和量测噪声方差阵R。但Sage-husa自适应滤波噪声参数估计算法与Kalman滤波公式的推导都是直接在时域上进行的，滤波器与估值器之间存在相互耦合，容易造成滤波发散[7]。从频域角度分析，系统噪声主要表现为低频噪声，而量测噪声表现为宽带噪声，因此，量测噪声方差可通过频带分割进行分离。量化噪声在提高数据采样率后会显著降低，一般情况下可以忽略。Allan方差滤波器为带通滤波器，部分低频噪声可直接被滤除，则宽频噪声的Allan方差值可近似为量测噪声的方差：

因此我们可以采用 Allan方差来估计量测噪声的方差。计算取样间隔为最短采样时间0τ时的Allan方差，得到如下递推形式：

联立式(10)和式(11)，量测噪声方差可表示为：

式中k=2,3,…，初始值任意选取。

这便是量测噪声方差的解耦估计方法，该方法中量测噪声方差的估计过程与 Kalman滤波过程完全独立，避免了滤波器与估值器间的相互耦合,可以有效降低滤波发散的风险。

2.3 解耦自适应Kalman滤波算法

采用Allan方差分析法估计量测噪声的方差参数，将此量测噪声方差估值器引入到 Sage-husa自适应滤波的滤波框架中[7-8]，构建解耦自适应Kalman滤波方程为：

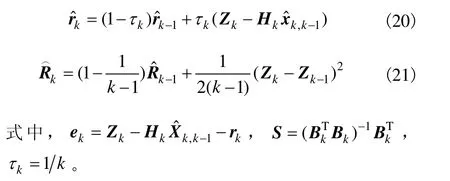
式(13)～(21)就构成了解耦自适应Kalman滤波器，其中式(21)为基于Allan方差的量测噪声方差估值器。交替运用上述公式，便可估计出系统状态和量测噪声统计特性，进而有效抑制陀螺随机噪声。

3 FOG随机噪声的滤波试验

为验证本文提出的解耦自适应 Kalman滤波方法在消除陀螺随机噪声中的有效性，对实验室X、Y、Z三个轴向FOG分别进行静态实测数据试验。采用本文提出的解耦自适应滤波方法与标准 Kalman滤波进行对比，可得滤波前后FOG输出数据对比曲线如图4～6所示。表2给出了滤波前后三个轴向FOG的输出信号统计特性对比。

图4 X陀螺滤波前后输出数据比较Fig.4 Output data comparison ofXgyro after filtering

图5 Y陀螺滤波前后输出数据比较Fig.5 Output data comparison ofYgyro after filtering

图6 Z陀螺滤波前后输出数据比较Fig.6 Output data comparison ofZgyro after filtering

表2 滤波前后三个FOG输出信号统计特性Tab.2 Statistical properties of FOG output signal after filtering

数据处理结果表明：对比三组FOG原始输出数据及滤波后输出数据曲线可以看出，滤波后的FOG随机噪声明显减小，而且相比标准 Kalman滤波，本文提出的解耦自适应 Kalman滤波方法对随机噪声的抑制效果更明显。

通过对滤波前后FOG输出信号的统计特性表可以对比看出，滤波前后随机噪声均方差变化较明显，在保证无偏估计的前提下，本文提出的滤波方法有效抑制了随机噪声的分散程度。通过对实测数据试验结果分析可以看出，本文提出的滤波方法具有更高估计精度，能有效抑制FOG随机噪声。

4 结 论

采用时间序列分析法对 FOG实测数据进行了AR(2)建模。提出了一种解耦自适应Kalman滤波方法，方法采用 Allan方差分析法估计量测噪声的方差，Kalman滤波过程与量测噪声方差的估计过程完全独立，避免了 Kalman滤波器与量测噪声估值器间的相互耦合。实测数据试验结果表明，采用本文方法能够有效抑制FOG输出信号中的随机噪声。

（References）：

[1]易康，李廷志，吴文启.FLP滤波算法在光纤陀螺信号预处理中的应用[J].中国惯性技术学报，2005，13(5)：58-62.YI Kang,LI Ting-zhi,WU Wen-qi.Application of forward linear prediction filter in signal process of FOG[J].Journal of Chinese Inertial Technology,2005,13(5):58-62.

[2]王立辉，孙枫，季强，等.LMS自适应滤波算法在FOG数据处理中的应用[J].系统工程与电子技术，2010，32(5)：1047-1050.WANG Li-hui,SUN Feng,JI Qiang,et al.Application of LMS adaptive filtering algorithm in FOG data processing[J].Journal of Systems Engineering and Electronics,2010,32(5): 1047-1050.

[3]Ding Weidong,Wang Jinling,Rizos C.Improving adaptive Kalman estimation in GPS/INS integration[J].The Journal of Navigation,2007,60: 517-529.

[4]Sage A P,Husa G W.Adaptive filtering with unknown prior statistics[C]//Proceedings of Joint Automatic Control Conference,Boulder Colorado,1969: 760-769.

[5]王省书，黄宗升，周朴，等.激光陀螺随机漂移的数字滤波方法比较[J].中国激光，2006，33(11)：1547-1551.WANG Xing-shu,HUANG Zong-sheng,ZHOU Pu,et al.Comparative study on digital filtering on the random drift of laser gyro[J].Chinese Journal of Lasers,2006,33(11):1547-1551.

[6]Allan W D.Statistics of atomic frequency standards[C]//Proceedings of the IEEE,1966,54(2): 221-230.

[7]魏伟，秦永元，张晓冬，等.对Sage-Husa算法的改进[J].中国惯性技术学报，2012，20(6)：678-686.WEI Wei,QIN Yong-yuan,ZHANG Xiao-dong,et al.Amelioration of the Sage-Husa algorithm[J].Journal of Chinese Inertial Technology,2012,20(6): 678-686.

[8]Enbo S.An improved real-time adaptive Kalman filter for low-cost integrated GPS/INS navigation[C]//Proceedings of 2012 International Conference on Measurement,Information and Control.Harbin,China,2012: 1093-1098.

De-noising method of decoupling adaptive Kalman filter for FOG signal

LI Yang,HU Bai-qing,QIN Fang-jun,ZHA Feng
(Department of Electrical Engineering,Naval University of Engineering,Wuhan 430033,China)

To solve the problem of random noises in the output data of fiber optic gyroscope(FOG),a decoupling adaptive Kalman filter is proposed for FOG signal de-noising.The parameter of the measurement noise variance is estimated by Allan variance analysis method.The processes of measurement noise variance estimation and Kalman filter are independent of each other.Therefore,the coupling between Kalman filter and estimator of measurement noises is avoided.The model of FOG random noise is established by using time series analysis method.Then,based on the second-order regression model,the collected random noise of FOG measured data is tested by using the proposed filtering method.Compared with traditional method,the proposed filtering method has better de-noising effect,and the mean square error of noise can be reduced by at least 40%.

fiber optic gyroscope; ARMA model; Allan variance; decoupling; adaptive filter

U666.1

：A

1005-6734(2014)02-0260-05

10.13695/j.cnki.12-1222/o3.2014.02.022

2013-11-21；

：2014-03-04

国家自然科学基金（61374206，61104184）；国家重大科学仪器开发专项（2011YQ12004502）；海军工程大学自然科学基金（HGDQNJJ12028）资助。

李杨（1987—），男，博士研究生，从事惯性技术及应用研究。E-mail：hgdh_ly@126.com

联 系 人：覃方君（1979—），男，讲师，从事惯性导航及组合导航系统技术研究。E-mail：haig2005@126.com