微机电陀螺信号盲均衡迭代反卷积算法

姜 涛，王建中，施家栋

（北京理工大学 爆炸科学与技术国家重点实验室，北京 100081）

微机电陀螺信号盲均衡迭代反卷积算法

姜 涛，王建中，施家栋

（北京理工大学 爆炸科学与技术国家重点实验室，北京 100081）

小型移动机器人在未知环境下运行，陀螺所受噪声干扰无法建立有效的数学模型，需要仅从观测信号中把噪声去除，并估计出原始信号，根据该特点提出一种微机电陀螺信号盲均衡迭代反卷积算法。该算法利用横向滤波器对陀螺信号进行反卷积运算，使用贝叶斯方法对信号进行估计，建立了误差函数并与 LMS算法组合，实现了均衡器参数的自动调整，在小型移动机器人上进行了算法实验验证。实验结果表明，该算法可以有效分离角速度信号与噪声信号，其噪声信号幅值减小约 10倍，移动机器人运行275.41 s抵达终点的偏航角误差从13°下降到1.46°。

移动机器人；MEMS陀螺；盲均衡；反卷积；滤波器

微小型移动机器人的智能化水平逐步提高，将广泛的应用于城市作战中。但是由于其体积小续航能力较差，通常是由士兵背负到作战区域，再实施相关战术任务。所以对移动机器人的体积和重量有严格要求，从而导致此类机器人无法使用体积与重量较大的光纤陀螺等传感器进行导航定位。虽然微机电陀螺的体积与重量均满足要求，但其传感器加工精度与抗干扰能力较差，需对其输出信号进行复杂的数据处理。

FIR滤波和IIR滤波或其二者的组合所构成的低通滤波器与陷波器[1-2]，可以消除噪声干扰，但此类滤波器缺点是需要较多的系数去近似期望响应，会造成较大滞后。采用基于AR模型的Kalman滤波算法可以有效的抑制噪声[3-4]，其状态的每次更新都是由前一次估计和新的输入数据计算得到，具有较高的实时性。小波变换与多分辨率分析原理方法[5-6]，可以有效地消除陀螺的随机游走。

本文提出一种盲均衡迭代反卷积算法对微机电陀螺信号进行处理，该算法可有效分离陀螺信号与噪声信号，提高了陀螺数据的输出精度，减小了噪声对信号的影响。

1 盲均衡迭代反卷积算法

微机电陀螺在测量数据时，由于传感器自身的精度误差与外界干扰的共同作用下，会产生零偏和随机游走。为了便于对角速率信号进行分析，将微机电陀螺及其内部信号进行建模，陀螺信号盲均衡模型如图1所示，x(n)为待检测平台角速率真值，该真值通过微机电结构转换成电信号，但在转换过程中信号会产生失真体现为零偏，该信号失真可认为是微机电结构误差与角速率真值进行卷积运算所产生的。之后与噪声信号v(n)相加体现为随机游走，最终产生陀螺传感器的输出信号u(n)。盲均衡器是对输入信号u(n)进行迭代反卷积运算与非线性估计[7-8]，使盲均衡器的输出xˆ(n)尽量接近输入数据x(n)。盲均衡器内部结构如图2所示，e(n)为迭代反卷积的估计误差[9-10]；wˆ(n)为横向滤波器的权值系数，根据 LMS算法与迭代反卷积的估计误差，对横向滤波器的权值系数进行实时更新，实现了自适应调整；g(·)为非线性估计器。

图1 陀螺信号盲均衡模型Fig.1 Blind equalization for gyroscope signal

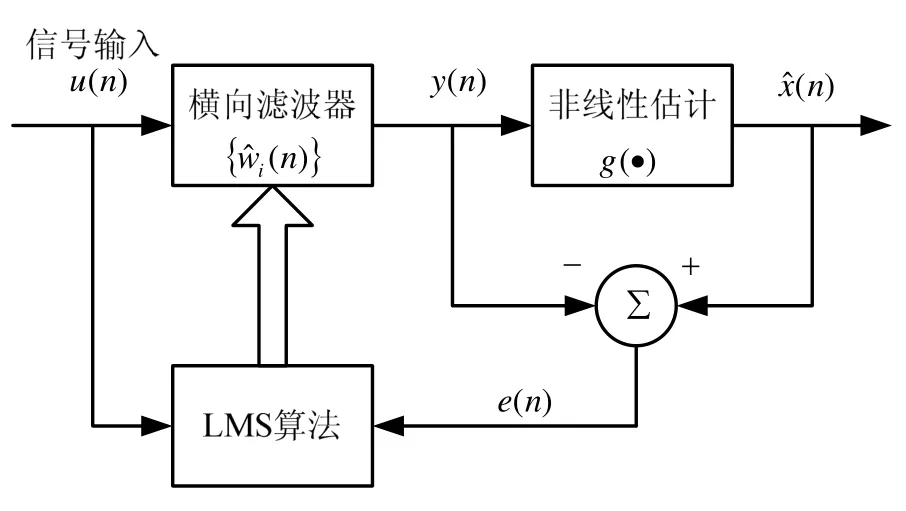
图2 盲均衡器结构Fig.2 Structure of blind equalization

1.1 迭代反卷积

反卷积是指通过测量输出和已知输入，重构未知输入的过程。利用已知输入自身的先验信息可知相关干扰特性，使均衡器的输出尽量接近输入，在解卷积前需要对输入信号进行辨识。

横向滤波器中输出信号与期望信号之间采用信号最小均方差准则为最优，基于该准则的横向滤波器可以得到线性的解析解。通过最小均方误差函数可以得到横向滤波器权值系数。

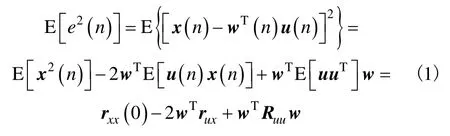
令式(2)等于零，则有权值系数:

在解卷积时，需要记录当前采样点之前的采样点的个数P，有作为横向滤波器的输入序列，通过对输入信号的辨识得到初始化权值系数，为。用迭代法进行解卷积运算，在进行n次迭代后得到反卷积序列的输出

1.2 贝叶斯估计

由图 2所示输入信号进行反卷积后，输出信号y(n)输入给非线性估计器。该观测值y(n)由x(n)决定，并产生x(n)的估计为观测值y(n)的函数。有

建立代价函数的均方误差函数为：

将式(8)带入式(6)中，可得：

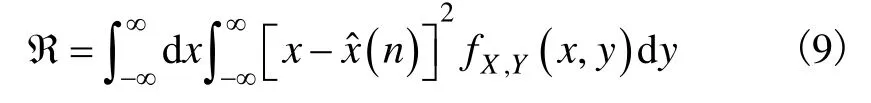
由贝叶斯公式有：

式中，fX(x|y)为已知y时x的条件概率密度函数，fY(y)为y的边缘概率密度函数，式(10)带入式(9)中，

fY(y)为非负，则可通过求式(11)中的内积最小化来得到风险函数ℜ最小，令L表示式(11)的内积，并求导，得

该式的解为唯一最小值。根据贝叶斯估计有

式中，fY(y|x)为给定x时y的条件概率密度函数，fX(x)为x的边缘概率密度函数，则有：

根据图1与图2中所建立的模型，观测值y(n)为横向滤波器输出端的反卷积序列，由估计数据序列x(n)与噪声v(n)组成，且x(n)均值为零、方差为1，v(n)为均值为零的白高斯噪声，与x(n)统计独立。可表示为

式中，c0为比例因子略小于1，从而使。则有

将式(17)带入式(15)中，得：

1.3 误差函数与LMS算法

在n次迭代后得到估计值，为了使后续估计值有较高的精度，采用自适应参数估计结构，根据估计值的误差自动调整滤波器参数。将非线性估计当作期望响应，则迭代反卷积过程的估计误差为：

LMS算法采用瞬时平方误差的梯度，其自适应方程为：

式中，μ为步长参数，为权值系数的估计，利用该值估计出，对横向滤波器的权值系数进行更新，实现了自适应调整，提高了估计精度。

2 实验验证

2.1 实验平台及传感器参数

小型移动机器人平台如图3所示，利用该平台进行算法验证。选择的微机电陀螺参数如表1所示，陀螺重量为23 g，适合安装在微小型移动机器人内。

实验验证地图及移动机器人运动轨迹如图 4所示，该实验环境为北京理工大学出版楼6楼。首先，移动机器人放置起点处，延点划线运动至折返点，在折返点做180°转向后，按照原路径返回至起点。实验全程采集微机电陀螺数据，并使用所设计的算法进行处理，通过该算法得到平台自身的定位信息。平台全程运行时间为4.6 min（275.41 s)。

图3 小型移动机器人Fig.3 Mini-mobile robot

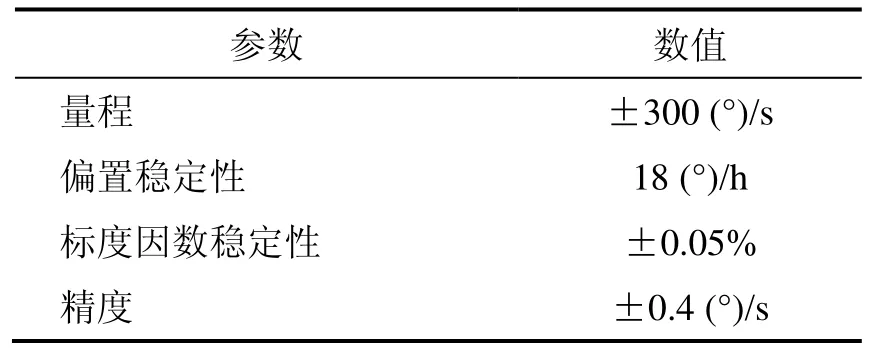
表1 微机电陀螺参数Tab.1 Performance specification for MEMS gyroscope

图4 建筑物内部地图及移动机器人运行轨迹Fig.4 Building interior map and mobile robot trajectory

2.2 结果分析

根据图3中小型移动机器人建立载体坐标系，平台前进方向为X轴（滚转角)正向，Y轴（俯仰角)为与X轴垂直并处同一水平面，Z轴（偏航角)为垂直水平面，向上为正向。

实验记录了未对陀螺信号进行盲均衡反卷积算法处理时，所得三轴角速度数据，如图5所示。可以看出移动机器人在水平地面运动，滚转角与俯仰角有较大噪声干扰，是由于机器人自身机械结构与地面相互作用所产生的。移动机器人在运动至楼道各个转弯处时，偏航角有明显数据波动与之对应，也可见较大噪声干扰存在。

图6所示为对陀螺信号进行盲均衡反卷积处理后，所得到的数据结果。从中可以看出相对于未处理时，滚转角和偏航角幅值下降约10倍，有效地抑制了干扰。偏航角相对未处理时幅值没有下降，但噪声信号有明显削弱。由此可知，该盲均衡迭代反卷积算法可以很好的区分角速度信号与噪声信号。

图7所示为陀螺原始信号幅值谱，该图可以反映信号在各频率下的能量成分。从图中可以看出，滚转角X与俯仰角Y方向上以40 Hz为中心有较多高频干扰，这是由于电机与机器人的行走机构在地面运行时产生的振动。在偏航角Z方向上也有噪声干扰存在，但幅值相对较小。

图8为盲均衡信号的幅值谱，如图所示陀螺信号经过盲均衡器的处理后，滚转角X与俯仰角Y方向上的高频干扰全部消失，低频干扰的幅值也有大幅减小。在偏航角Z方向上大部分干扰被消除，而有用信号的幅值并没有减小，说明该算法可以有效消除系统噪声干扰，并保留有效信号。

在实验验证过程中，移动机器人沿着预定路线行走，经过折返点返回至起点。理论上陀螺所测滚转角X与俯仰角Y均为0°，偏航角Z由于是返回方向应为+180°或-180°。表2所示为完成预定行走路径后，陀螺所测量机器人在终点时的角度。为了对比算法效果，同时列出未经信号处理时的移动机器人终点定位角度。从表2可以得出本文所提出的盲均衡迭代反卷积算法在处理微机电陀螺信号时，可以有效去除噪声干扰，使偏航角误差从13°下降到1.46°，提高了移动机器人定位精度。

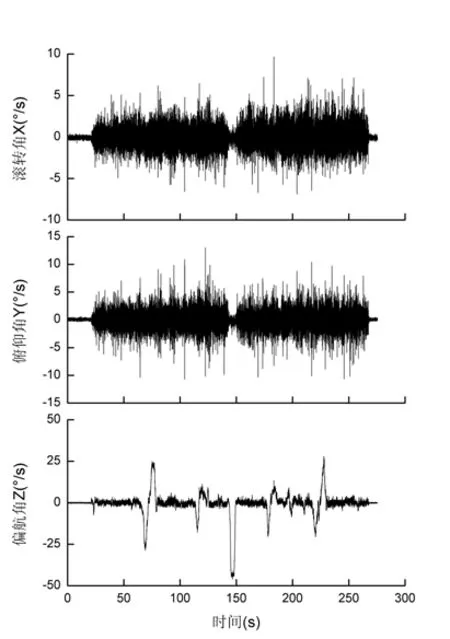
图5 陀螺输出三轴原始信号Fig.5 3-axis original signal for gyroscope

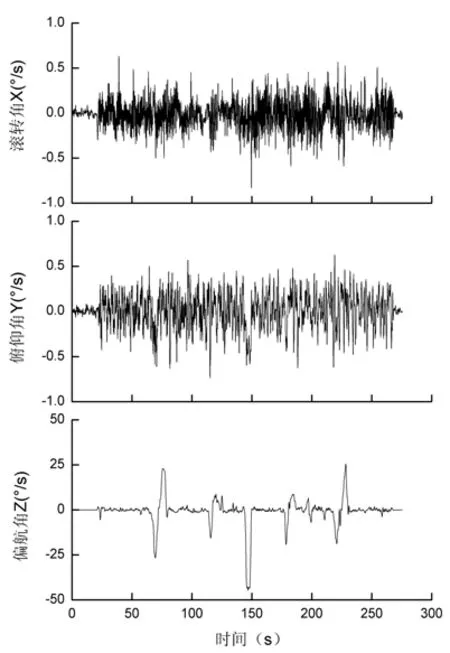
图6 陀螺信号盲均衡反卷积结果Fig.6 Blind equalization result for gyroscope

图7 三轴原始信号幅值谱Fig.7 Amplitude spectrum of 3-axis original signal

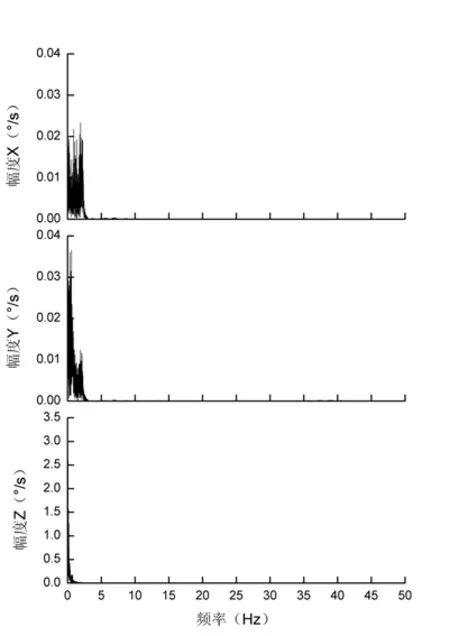
图8 盲均衡信号的幅值谱Fig.8 Amplitude spectrum of blind equalization signal

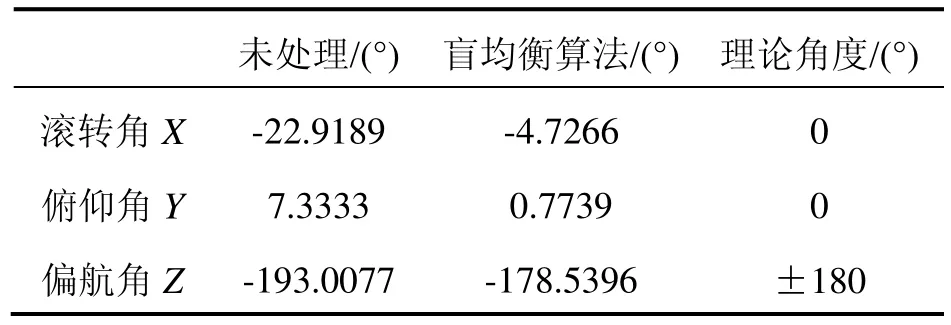
表2 移动机器人运动陀螺所测量的角度Tab.2 Angle of measuring for robot movement

3 结 论

本文提出一种微机电陀螺信号盲均衡迭代反卷积算法，通过对微机电陀螺信号产生原理的分析，利用横向滤波器对陀螺信号进行反卷积运算，使用贝叶斯估计对角速度信号进行非线性估计，并建立了误差函数与LMS算法组合，实现了均衡器参数的动态调整。在移动机器人上进行了算法验证，实验结果表明，该算法可以有效地分离角速度信号与噪声信号，提高了移动机器人的定位精度，其算法可为相关领域应用提供借鉴。

（References):

[1]Sun F,SUN W.Mooring alignment for marine SINS using the digital filter[J].Measurement,2010,43(10):1489-1494.

[2]Beylkin G,Lewis R D,Monzon L.On the design of highly accurate and efficient IIR and FIR filter[J].IEEE Transactions on Signal Processing,2012,60(8): 4045-4054.

[3]Sabatelli S,Galgani M,Fanucci L,et al.A double-stage kalman filter for orientation tracking with an integrated processor in 9-D IMU[J].IEEE Transactions on Instrumentation and Measurement,2013,62(3): 590-598.

[4]Bekkeng J K.Calibration of a novel MEMS inertial reference unit[J].IEEE Transactions on Instrumentation and Measurement,2009,58(6): 1967-1974.

[5]Peesapati R,Sabat S L,Anumandla K K,et al.Design and implementation of a realtime co-processor for denoising fiber optic gyroscope[J].Digital Signal Processing,2013,23(5): 1813-1825.

[6]Broquetas A,Cimeron A,Gelonch A,et al.Track detection in railway sidings based on MEMS gyroscope sensors[J].Sensors,2012,12(12): 16228-16249.

[7]Chesneau C,Fadili J.Wavelet-based density estimation in a heteroscedastic convolution model[J].Communications in Statistics-Theory and Methods,2013,42(17): 3085-3099.

[8]赵永平，许鹏，杨硕.用窗口卷积实现反卷积的算法研究[J].电子学报，2005，33(8)：1533-1536.ZHAO Yong-ping,XU Peng,YANG Shuo.Study on an algorithm of deconvolution via window convolution [J].Chinese Journal of Electronics,2005,33(8):1533-1536.

[9]毛玉良，陈家斌，宋春雷，等.捷联惯导姿态误差模型分析[J].中国惯性技术学报，2013，21(2)：182-185.MAO Yu-liang,CHEN Jia-bin,SONG Chun-lei,et al.Analysis of attitude error models of strapdown inertial navigation system[J].Journal of Chinese Inertial Technology,2013,21(2): 182-185.

[10]Bhatt D,Aggarwal P,Bhattacharya P,et al.An enhanced MEMS error modeling approach based on nu-support vector regression[J].Sensors,2012,12(7): 9448-9466.

Iterative deconvolution algorithm of blind equalization for MEMS gyroscope signal

JIANG Tao,WANG Jian-zhong,SHI Jia-dong
(State Key Laboratory of Explosion Science and Technology,Beijing Institute of Technology,Beijing 100081,China)

The mathematical model of a mobile mini-robot running in unknown environment cannot be effectively built due to gyroscope’s noise interference,and needs to remove the noise only from the observing signal and estimate the original signal.In this paper,an iterative deconvolution algorithm of blind equalization for MEMS gyroscope signal is presented.The transversal filter for the gyroscope signal to implement deconvolution calculation is employed,and the signal is estimated by Bayesian methods.The error function is established and combined with LMS algorithm to achieve the automatic adjustment of equalization parameter.The verification of the algorithm is carried out on the mini-mobile robot.The experiment results show that the angular velocity and noise signals can be effectively extracted from the mixed signals,and the amplitude of noise signal is decreased to about 1/10 of the original.After the mobile robot has run 275.41 s,the error of its final yaw angle for mobile robot is reduced from 13° to 1.46°.

mobile robot; MEMS gyroscope; blind equalization; deconvolution; filter

U666.12

：A

1005-6734(2014)02-0237-05

10.13695/j.cnki.12-1222/o3.2014.02.018

2013-11-20；

：2014-03-17

国防基础科研计划资助项目（B2220110013）；总装预研项目（104060202）

姜涛（1984—），男，博士研究生，从事微小型无人作战平台导航研究。E-mail：eli_jiang@126.com

联 系 人：王建中（1963—），男，教授，博士生导师。E-mail：cwjzwang@bit.edu.cn