基于遗传算法的条状文字碎片复原算法
苏小朋,杨昔阳,2
(1.泉州经贸职业技术学院,福建 泉州 362000;2.泉州师范学院数学与计算机科学学院,福建 泉州 362000)
基于遗传算法的条状文字碎片复原算法
苏小朋1,杨昔阳1,2
(1.泉州经贸职业技术学院,福建 泉州 362000;2.泉州师范学院数学与计算机科学学院,福建 泉州 362000)
规则碎片复原是图片复原领域的一个研究热点。本文以碎片的边缘像素为特征,通过定义恰当的遗传操作和变异操作,采用遗传算法建立了一种普适性、推广性较好的数学模型。实验表明,利用这种算法对中英文条状碎片进行复原,效果良好。
条状文字碎片;碎片复原;遗传算法
图像碎片的复原是计算机视觉领域中的一个新颖且典型的应用,它主要研究如何借助计算机确定碎片的特征,再采用适当的数学模型确定碎片在原图像中应有的位置,从而达到还原图片的目的。
目前关于碎片复原研究有很多,它们集中把图像碎片的几何轮廓当作碎片特征,再通过某些数学模型逐步完成全局复原。几何信息的提取方法主要包括∶(1)轮廓线匹配法[1];(2)多尺度轮廓匹配法[2-3];(3)角序列匹配法[4];(4)边界链码法[5]。
条状碎纸机是现实生活中的一类常见的碎纸方式。针对这种特定的文字碎纸复原,国内有一些人对此提出了解决方法[6-7],但当碎片规模足够大时,通过经典的优化算法往往很难得到最优解。为此,本文提出了一种基于遗传算法的文字碎片复原方法。
1 遗传算法简介
在生物进化过程中,种群总能通过不断的进化来适应环境。遗传算法正是这么一种模拟生物进化的智能算法。这种算法已经简洁而又高效地解决了若干重要的问题。遗传算法通过一系列带有随机因素的遗传操作和变异操作来模拟自然选择,具有非常强的适应性,往往被用于求解一些经典算法难以求解的优化问题。因为遗传算法是一种模拟生物进化的算法,因而这种算法中的专业术语也往往和生物进化有关。在一个优化问题中,可行域中的点经过适当编码后,称为染色体。每个可行解对应的目标函数值称为该染色体的适应值。一定规模的染色体组成一个集体,称为一代的种群。在每代种群中,染色体不断被遗传操作和变异操作更新,这些根据适应值精心设计的遗传、变异操作可以以极高的概率保证各代的平均适应值越来越好,即在种群规模和代数足够大的时候,可以保证最优的染色体以百分之百的概率逼近最优解。
2 模型的建立和求解
假定条状文字碎片来源于同一张纸质文档,它们的边缘在裁减中没有被损坏,且该张纸片的所有碎片保存完整。每张条状碎片的大小相同,所以没有办法采用现有文献中的各种拼接算法,因为这些算法大都是基于碎片的几何形状来完成拼接的。图1给出了若干条状碎片的示意图,限于篇幅,并非所有图片全部被列出。笔者在实验过程中也尝试利用文字识别的方法来确定两张图片是否相邻,但庞大的计算量使这种算法缺乏可执行性。因此本文以两张条状碎片边缘像素的匹配程度为相邻程度的指标,建立了一个使整体匹配程度最优的优化模型,并通过遗传算法进行编码和求解.对中英文条状碎片的拼接表明了这种解法的实用性和可行性。

图1 若干条状碎片
2.1 复原模型的建立
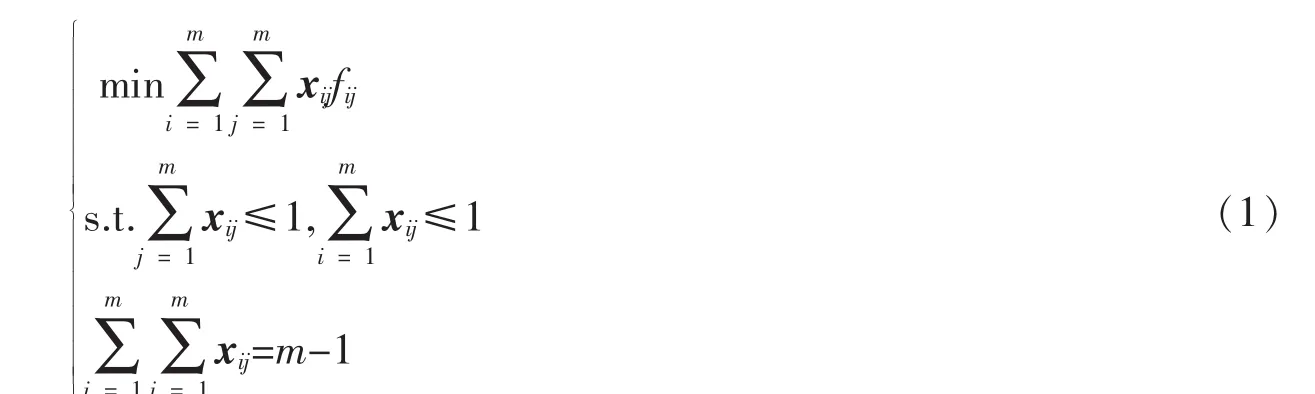
提取碎片i最右边一列的灰度值Ri和碎片j最左边一列的灰度值Lj,用两者的差异来构建碎片i和碎片j左右相邻的匹配度fij,即令

2.2 遗传算法的遗传和变异操作
在求解模型(1)时,采用从左到右的图片的序号为编码构造染色体。显然一组这样的编码和一个解矩阵[xij]mxm是等价的,例如如果已知碎片i和碎片j左右相邻,那么便可知=1,反之亦然。采用模型(1)的目标函数作为适应值函数。在进化中,适者生存,所以在遗传算法运行过程中,会不断地选择优者保留下来,同时也不断地选择劣者淘汰下去。在每代中,使用适应值处于前50%的染色体繁衍下一代。
恰当的遗传操作应该使得染色体不断朝着优化目标函数的方向进化,它可以保证遗传算法具有局部寻优的能力。随机选择两个适应值较好的染色体,采用“顺序交叉法”方式作为遗传操作函数。从父代A随机选一个编码子串,放到子代A′的对应位置;子代A′空余的位置从父代B中按B的顺序选取(与己有编码不重复)。同理可得子代B'。例如

变异操作是指依据变异概率将个体编码串中的某些数值用其它值来代替。变异操作是产生新染色体的辅助方法,它反映了遗传算法的全局搜索能力。通常可以取变异概率为20%。采用随机交换染色体两个元素或者两个片段的方法构造变异函数。
种群的规模是指在一代中染色体的个数。通常比较大的种群规模有助于更准确地找到优化模型的满意解,但也需要更长的时间。在解决模型(1)的过程中,我们让种群规模取常数400。
遗传运算的终止条件为进化代数达到500代,也就是说当遗传算法运行500轮之后,最后一代的最优解即为解决模型(1)的满意解。用户根据给定的结果进行判断,如果有必要,可以根据其中明显的错误修改匹配度矩阵,重新运行遗传算法。终止代数设置得越大,可以以更大的概率得到更精确的结果,但也需要更长的时间。
遗传算法的流程图如图2所示。在遗传操作中,选择适应值较好的前25%的染色体直接进入子代,其余75%的子代染色体由本节介绍的“顺序交叉法”产生,其流程图如图3所示。而在变异操作中,根据变异概率,随机从子代中挑选染色体交换其中两个元素或者两个片段进行重新排序。
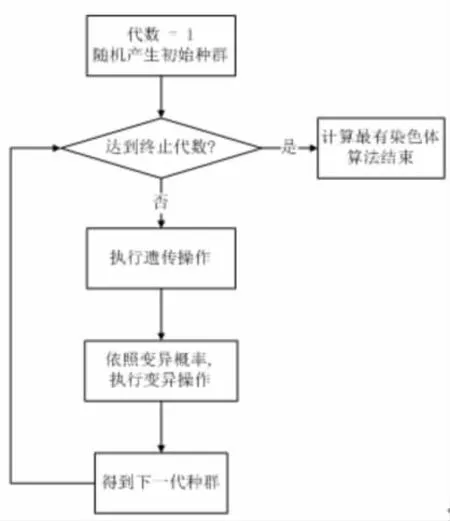
图2 遗传算法流程图

图3 遗传操作流程图
2.3 结果
针对中、英文各一张纸质材料进行纵向裁剪(碎片如图1所示),切割成19条条状碎片。通过Matlab提取每张碎片的左右边缘灰度值,对全白的边缘(很有可能是边界)进行特殊处理。采用遗传算法对模型(1)进行求解,经过500轮迭代,复原之后的中英文效果图如图4所示。在迭代过程中,每一代的最优染色体的适应值、平均适应值如图5所示。

图4 复原效果图
3 总结
采用遗传算法对条状文字碎纸进行复原。采用条状碎片边缘灰度值的匹配程度作为衡量碎片是否左右相邻的指标,建立了一个整体匹配度最优的复原模型,并利用遗传算法对该问题进行编码和求解。针对两张中、英文文件的条状碎片数据进行拼接复原,由于条状碎片边缘有足够的灰度值信息,因而利用遗传算法可以一次性得到正确结果,无须人为调整。表明本文采用的遗传算法是一种解决条状复原模型的切实可行的算法。

图5 适应值函数
[1]WOLFSON H J.On curvematching.[J].IEEE T ransactionson P attern A nalysisand M achine I nteigence,1990,12(5):483-489.
[2]LEITAO,H C,STOFIJ.A multiscalemethod forthereassembleoftwo-dimensional fragmented objects[J].IEEE Transact ions on Pattern Analysis and Machine Intelligence,2002,24(9):1239-125l.
[3]朱延娟,周来水,张丽艳,等.基于Hausdorff距离的多尺度轮廓匹配算法[J].中国机械工程,2004,15(17):1553-1561.
[4]周丰,黄晓呜.基于角序列的二维碎片轮廓匹配方法[J].科学技术与工程,2007,7(15):3757-3760.
[5]饶芮菱,金雪峰,鲁怀伟.基于链码的二维碎片轮廓匹配算法[J].计算技术与自动化,2007,26(2):34-37.
[6]杨雯雯,陶佳琪,郑路通,等.单页单面汉字纵横切碎片拼接复原算法[J].运城学院学报,2013(5):16-20.
[7]刘俊玮,王子豪,宋嵩焘,等.条状碎片文件自动复原的探讨与研究[J].数学学习与研究,2014(1):115-116.
(责任编辑:朱联九)
An GA Based Automatic Stitching Technology of Strip-shaped Pieces
SU Xiao-peng1,YANG Xi-yang1,2
(1.Quanzhou Vocational College of Economics and Business,Quanzhou 362000,China 2.School of Math and Computer Science,Quanzhou Normal University,Quanzhou 362000,China)
The restoration technology of strip-shaped pieces isone of the hot topics in the field of picture restoration.Using gray degrees in the edges as the characteristics,and after adequate-definite GA operation and mutation operation,digital model,universaland general in solving sim ilar questions,is established based on GA algorithm in this paper.The experiment shows that the proposed GA algorithm hasa good effectin solving the restoration of Chinese and English strip-shaped pieces.
strip-shaped pieces;fragment reassemblymethodology;GA algorithm
TP391.41
A
1673-4343(2014)02-0039-04
2013-12-08
福建省教育厅科技项目(JA12273,JK2013037);泉州市科技局科技项目(2012Z103)
苏小朋,男,福建泉州人,高级讲师。研究方向:基础数学。通讯作者:杨昔阳,男,福建泉州人,讲师。研究方向:模糊数学与人工智能。

