二维盲图像恢复算法的研究

庄金莲，陈佳丽

(龙岩学院数学与计算机科学学院，福建 龙岩 364012)

二维盲图像恢复算法的研究

庄金莲，陈佳丽

(龙岩学院数学与计算机科学学院，福建 龙岩 364012)

通过对现有的二维盲图像恢复算法的探讨，提出了两种基于L1双正则化的二维盲图像恢复算法。一种是最小化L2-L1代价函数，为了实现边缘保持和噪声抑制;另一种是通过最小化L1-L1代价函数来处理非高斯噪声的情况。所提的算法是一种广义的梯度算法，它通过引入绝对值函数的弱导数来处理不可微的情况。实验结果表明，与NAS-RIF算法和DR算法相比，所提出的两种二维算法能够更快速地获得好的图像估计。

盲图像恢复；L1双正则化方法；二维实现算法；广义梯度算法

图像恢复广泛应用于医疗图像、天文成像、遥感成像、显微镜成像等当前研究的热点领域。近些年来已提出许多盲图像复原算法，主要分为两类。第一类是将PSF的估计与恢复原始图像的过程分成两个不同的过程，先估计PSF,再采用现有的图像恢复方法进行图像的复原。这类方法的特点是计算量较少，主要采用模型参数法，典型的有先验模糊辨识方法。第二类是同时估计PSF和恢复原始图像，将PSF的估计与图像恢复的过程相结合。这类算法比较复杂，计算量较大，主要有模型参数法和非参数式的盲迭代法。在参数法中，如ARMA参数估计法[1]。在迭代法中，有Ayers和Dainty提出的迭代盲反卷积方法(IBD)[2]和D.Kundur等人提出的非负有限支撑域约束递归逆滤波法(NAS-RIF)[3]及其在此方法上的拓展，包括改进的NAS-RIF算法[4-5]等。

目前另一种研究方向是将经典图像恢复方法中的正则化理论[6]应用于盲图像恢复。典型的有You Yu-li和M.Kaveh提出的对称双正则化（SDR）方法[7]，Chan提出的总变分(TV)盲图像复原[8]和Chen Li提出的参数双正则化（PDR）方法[9]。

另外，根据程序实现方式，我们将现有盲图像恢复算法分为两类，一类是一维实现方法，如TV方法和PDR方法；另一类是二维实现方法，如DR方法和NAS-RIF算法。通常二维实现算法适用于处理大幅的图像且运行速度远远快于一维实现算法。

本文将L1范式应用于代价函数，提出了两种基于L1双正则化的二维盲图像恢复算法。通过对比实验研究表明所提出的两种二维算法能够更快速地获得好的图像估计和PSF估计。

1 图像模型与二维盲图像恢复方法

1.1 图像退化模型与恢复过程

通常图像的退化是由模糊和噪声两方面因素造成的。一般情况下，为简化计算，假设点拓展函数PSF为线性空间不变系统，噪声为加性噪声，那么二维的图像退化模型可用式(1)表示：

其中g(x,y)、f(x,y)、h(x,y)、n(x,y)分别表示单幅的退化图像，单幅、静态、单色的（简称为单通道）原始图像,点拓展函数PSF和加性噪声；⊗表示二维卷积算子。为了有效地采用二维实现方法，这里直接将一幅退化图像作为一个二维数字信号来进行处理。盲图像恢复问题就是根据观测到的退化图像g(x,y)以及原始图像f(x,y)和PSF的部分先验知识，获得原始图像的估计(x,y)，使之尽可能地接近原始图像f(x,y)。

1.2 经典的二维盲图像恢复方法

经典的二维盲图像恢复方法有D.Kundur等人提出的非负有限支撑域约束递归逆滤波(NASRIF)算法[8]和You Yu-li和M.Kaveh提出的对称双正则化SDR方法[14]。NAS-RIF算法假设图像是非负的，且具有已知的支撑域。该算法的优点在于代价函数是凸的，保证算法收敛到全局最小，算法稳定、收敛速度快，但是由于其滤波器是高通滤波器，必然存在高频噪声放大的问题，特别是对于信噪比较低的图像，复原效果不好。SDR方法将盲恢复问题看作是最小化一个双正则化的代价函数，把问题分解为模糊辨识和图像恢复两个过程，其中最小化过程采用基于共轭梯度法的替代最小化（AM）策略来实现。SDR方法没有考虑到图像和PSF的鲁棒性特点，因而存在边界处理的问题，而且当加性噪声不满足高斯分布时，SDR方法的恢复效果不佳。此外，SDR方法还要求PSF是对称的。

2 基于L1双正则化的二维盲图像恢复算法

由于L1范式[10-11]在统计估计问题上所获得的解更具鲁棒性。因此将L1范式应用于代价函数中，提出了2种基于L2-L1和L1-L1双正则化的二维盲图像恢复算法。在最小化过程中引进了一种基于广义共轭梯度法的替代最小化（AM）算法。

2.1 改进的代价函数

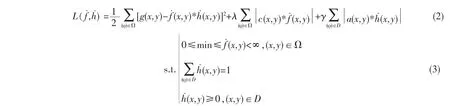
由于SDR方法的两项正则化项都采用L2范式的形式，存在边界问题，考虑用L1范式替代两项正则化项中的L2范式，提出了一个新的混合的L2-L1代价函数用于盲图像恢复。因此，本文所提出的基于L2-L1双正则化的二维盲图像恢复算法就是对下列的混合的L2-L1代价函数进行最小化：其中Ω⊂R2和D⊂R2分别表示原始图像和PSF的支持域，我们限定图像的支持域远远大于PSF的支持域，这样会使效果更明显。(x,y)和(x,y)分别表示原始图像和PSF的估计。代价函数中的c(x,y)和a(x,y)称为正则化算子，是一个高通滤波器,通常取Laplacaian滤波器；λ和γ是正则化参数。

L1估计方法对于非高斯分布非常有效。而且它不会过分扩大误差，因此当信号数据包含非高斯噪声颗粒的时候，L1估计方法相对于最小二乘（L2）方法更具鲁棒性。考虑将L1范式用于图像的逼真度这一项和两项正则化项中，提出了一个新的L1-L1代价函数用于盲图像恢复中。因此，本文所提出的基于L1-L1双正则化的二维盲图像恢复算法就是对下列的L1-L1代价函数进行最小化：

本文所提出的两个代价函数（2）和（4）由于使用L1范式的形式，因此都是非凸的（非光滑的）。

2.2 改进的最小化算法

所提出的代价函数使用L1范式，是非凸的，为了处理不可微的情况，引入弱导数的概念。绝对值函数的弱导数定义如下：

其中sign（·）的定义为

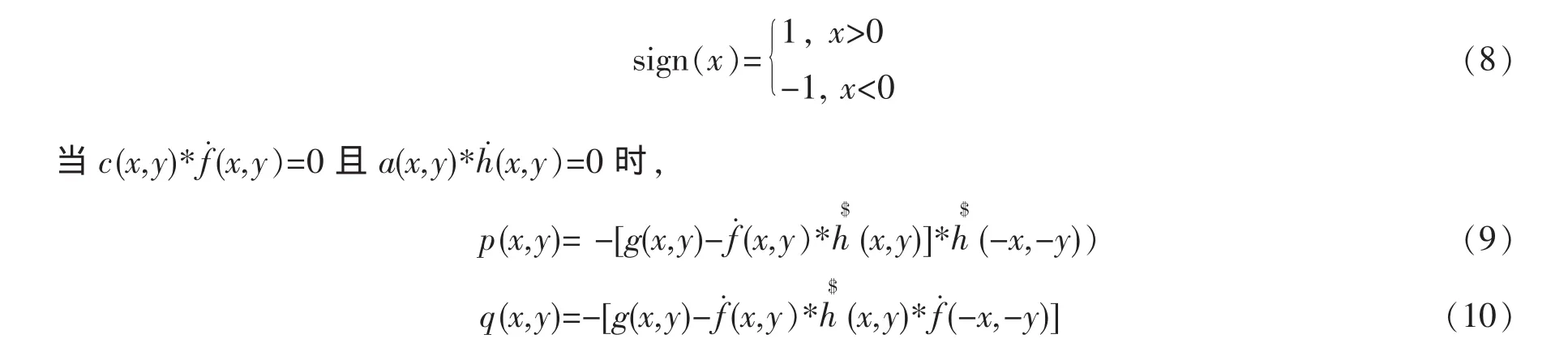
其中sign（·）的定义同式（8）。

为了以简洁的形式来描述所提出的算法，首先引入两个变形的符号函数：

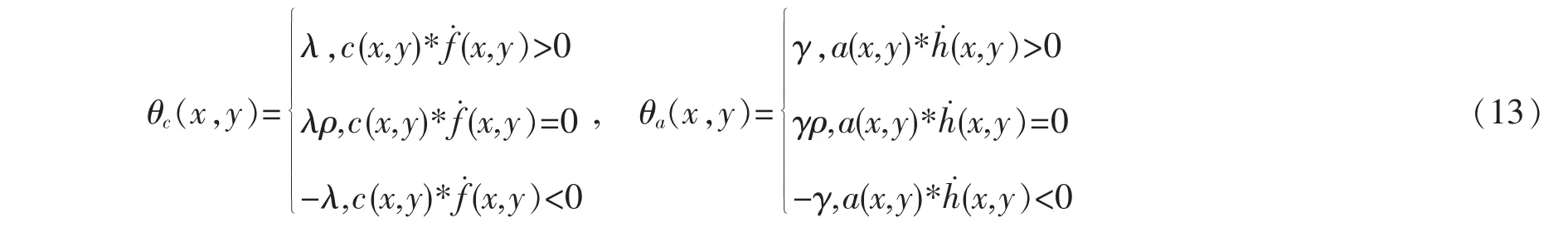
对于代价函数（4），再引入一个变形的符号函数：

那么式（6）、（11）和式（7）、（12）可分别改写成

现在来描述所提出的盲图像恢复算法。

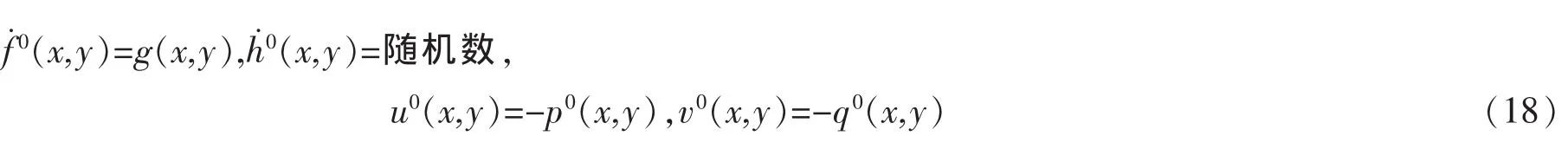
第2步，求解第k次迭代的图像估计。

更新广义共轭梯度向量

其中步长大小β0=1，当k≥1时

寻找αk满足下列条件

更新图像估计

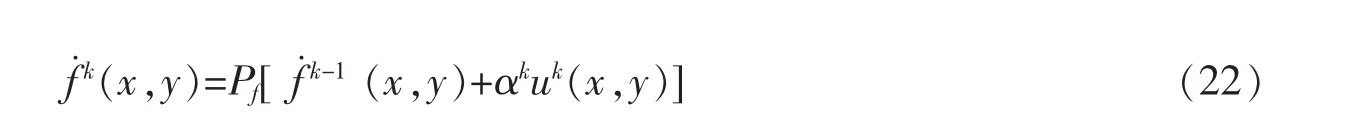
其中Pf表示的是式（3）的第一个约束条件的投影。

第3步，求解第k次迭代的PSF估计。

更新广义共轭梯度向量

寻找满足下列条件

更新PSF估计

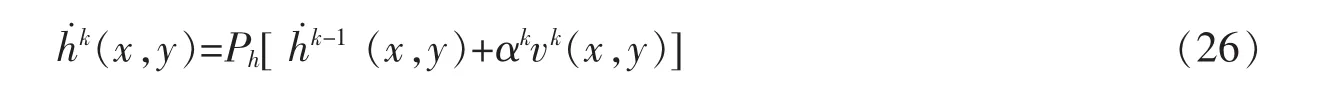
其中Ph表示的是式（3）的后两个约束条件的投影。

3 实验仿真

3.1 算法评价标准

本节中主要是结合主观评价方法和ISNR客观评价方法对我们的实验结果进行分析对比。ISNR是用以比较恢复图像与原始图像质量的参数，计算所得的值越大，说明图像质量越好。ISNR的计算公式如式（27）：

此外，针对双正则化方法，除了得到原始图像的估计之外，我们同时获得了PSF估计。为了评价PSF估计的精度误差，采用MSE客观评价方法来进行比较。MSE反映了所获得的PSF估计与原始PSF之间的误差，计算所得的值越小，说明PSF估计越精确。MSE的计算公式如式（28）：

对于所提出的算法中，参数ρ取值为0.01。

图1 原始utk图像

3.2 实验模拟结果

例1：考虑如图1所示的256×256的原始utk图像，首先用21×21的高斯模糊PSF对原始图像进行退化，然后再在模糊后的图像上附加混合随机噪声，最终生成退化图像，如图2（a)所示。

UTK图像是一幅均匀黑色背景的文本二值图像。当运行NASRIF算法时，参数假设δ=0.0138，（Nxu，Nyu）=（5,5）。图2（b)显示的是NAS-RIF算法运行30次迭代后的恢复图像。在原始图像支持域未知的情况下，我们采用一种寻找支持域的算法。对于UTK图像，这一过程运行了约11289.14 s。对于所提出的两种算法，参数假设λ=0.03，γ=108，且令最大迭代次数M=30，容差ε=0.01。图2（c)和图2(d)中显示了所提出的两种算法的恢复图像。

从主观评价角度来看，3幅恢复图像的视觉效果都比退化图像好。而我们所提出的两种算法获得的恢复图像在去模糊和去噪方面均明显优于NAS-RIF算法恢复的图像，UTK字母边缘轮廓和细节更加清晰，黑色背景噪声颗粒明显减少。

图2 例1中退化图像与3种算法的恢复图像

再者，我们还对受到其他类型噪声（高斯噪声和椒盐噪声）污染的UTK退化图像进行了盲恢复并进行比较。表1中列出了3种算法获得的图像估计的ISNR，PSF估计的MSE以及3种盲图像恢复算法的计算时间。

从表1中可以看出，与NAS-RIF算法相比，所提出的算法在高斯噪声和非高斯噪声（混合随机噪声和椒盐噪声）的环境下均能够以更快的速度获得更好的恢复图像和PSF估计。

例2：考虑如图3所示的256×256卫星图像，首先用5×5的高斯模糊PSF对原始图像进行退化，然后再在模糊后的图像上附加噪声强度为0.5的椒盐噪声，最终生成退化图像，如图4（a)所示。

图3 实时卫星图像

采用所提出的两种算法和传统的DR方法进行盲恢复。令最大迭代次数M=30，容差ε=0.01，参数λ=0.08，γ=108。这3种方法在同样的初始条件下运行，所得的恢复图像如图4（b)～图4（d)所示。

图4 例2中退化图像与3种算法的恢复图像

从主观评价角度来看，3幅恢复图像的视觉效果都比退化图像好。而我们所提出的两种算法获得的恢复图像在去模糊和去噪方面均明显优于DR算法恢复的图像，卫星图像边缘轮廓和细节更加清晰，尤其图4（d)中卫星图像上的线条被明显地恢复出来，且背景的噪声颗粒明显减少。

表2中列出了3种算法获得的图像估计的ISNR，PSF估计的MSE以及3种盲图像恢复算法的计算时间。

表2 3种算法恢复图像的客观评价结果

从表2中可以看出，与DR算法相比，所提出的算法在非高斯噪声（椒盐噪声）的环境下能够以更快的速度获得更好的恢复图像和PSF估计。

4 结论

基于L1双正则化方法，提出了两种改进的二维盲图像恢复算法。与DR方法不同的是，这两种算法分别采用L2-L1和L1-L1代价函数，而所提出的算法是一种广义的梯度算法，它通过引入绝对值函数的弱导数来处理不可微的情况。其中第2种算法更适合于处理非高斯噪声的情况。与NASRIF方法相比，这两种方法均不需要图像拥有已知的支撑域，且能同时获得PSF的估计。实验结果表明，与经典算法相比，所提出的两种二维算法能够更快速地获得好的图像估计。

∶

［1］CAMPISIP，EGIAZAR IAN K．Blind image deconvolution：theory and applications［M］．[s．l．]CRC Press，2007．

［2］AYERSGR，DAINTY JC．Iterativeblind deconvolutionmethod and itsapplications［J］．OptLett，1988，13（7）：547-549．

［3］KUNDUR D，HATZINAKOSD．A novelblind deconvolution scheme for image restoration using recursive filtering［J］．IEEE Trans Signal Process，1998，46（2）：375-390．

［4］NG M K，PLEMMONSR J，QIAO S．Regularization of RIF blind image deconvolution［J］．IEEE Trans Image Process，2000，9（6）：1130-1134．

［5］余昕，杨绿溪，邹采荣．基于确定性约束和局部空间自适应正则化的图像盲复原算法［J］．数据采集与处理，2002，17（2）：121-125．

［6］YOU Y L，KAVEH M．A regularization approach to blind restoration of images degraded by shift-variant blurs[C]／／Proceedingsof IEEEConference on Acoustics，Speech and Signal Processing．M ichigan：[s．n．]1995：2607-2610．

［7］YOU Y L，KAVEH M．A regularization approach to joint blur identification and image restoration［J］．IEEE Trans Image Process，1996，5（3）：416-428．

［8］CHAN T F，WONG C K．Total variation blind deconvolution［J］．IEEE Trans Image Process，1998，7（3）：370-375．

［9］LICHEN，KIM HUI YAP．A soft double regularization approach to parametric blind image deconvolu tion［J］．IEEE Trans Image Process，2005，14（5）：624-633．

［10］NIKOLOVAM．A variationalapproach to remove outliersand impulse noise［J］．JMath Imaging Vision，2004（20）：99–120．

［11］KARKKAINEN T，KUN ISCH K，MAJAVAK．Denoising ofsmooth imagesusing L1-fitting［J］．Computing，2005，74：353-376．

（责任编辑：朱联九）

Study of Two-Dimensional Algorithms for Blind Image Restoration

ZHUANG Jin-lian,CHEN Jia-li
(College of Mathematics and Computer Science,Longyan University,Longyan 364012,China)

By exploring the existing two-dimensional(2-D)algorithms for blind image restoration,this paper proposes two new two-dimensional algorithms for blind image restoration based on an L1 double regularization approach.One is formulated as the m inim ization of a L2-L1 cost function to achieve edge preservation and noise suppression.The other is viewed as theminimization of a L1-L1 cost function for blind image restoration under non-guassian noise environments.Thus a generalized gradientalgorithm is introduced by using aweak derivative of the absolute value function to dealw ith the non-differentiable case.Experimental results show that the proposed two-dimensional algorithms can obtain a better restored image and the estimated PSFw ith a faster speed than both the NAS-RIFalgorithm and the DR algorithm.

blind image restoration;L1 double regularization approach;2-D implementation algorithm;generalized gradientalgorithm

TP391．41

A

1673-4343（2014）02-0006-08

2014-02-28

龙岩学院服务海西面上项目（LYXY2011071）

庄金莲，女，福建晋江人，助教。研究方向：计算智能。