考虑锈蚀的钢结构地震易损性分析①
郑山锁,田 进,韩言召,徐 强,孙乐斌
(西安建筑科技大学土木工程学院,陕西 西安 710055)
0 概述
钢结构具有轻质高强和建造工业化的优点,但同时也存在着在耐腐蚀等方面的不足。钢结构在环境中服役时会因钢材的劣变引起结构的承载能力与刚度发生退化,当遭遇地震时结构现阶段具有的能力不能保证其在寿命期内完成其预定抗震功能。因此,在对不同服役时间的结构进行地震易损性评估时有必要考虑钢材锈蚀对结构整体抗震性能的影响。
目前对钢结构锈蚀的研究大多集中在材性层面,主要是以试验研究为主,但因试验条件、试验方法、试验性质等因素不同导致不同学者得出的结论差异性较大,所得出的数据及统计得出的关系式难以得到充分利用。到目前为止,尚未有比较成熟的关系式以供应用。而对构件层次的研究尚未清楚,现有文献大都只考虑均匀腐蚀。如文献[1]仅对构件截面进行简单折减,从而进行结构性能分析。涉及整体结构在寿命期内考虑材料劣变的抗震性能的鲜有研究。在桥梁结构方面,Betro[2]等对既有混凝土桥梁在结构劣化的情况下的抗震性能进行了评估,然而多数研究并未给出材料劣变对桥梁地震易损性的影响的时间效应与计算方法。本文在以上研究的基础上考虑钢材随服役时间的劣变过程对钢结构地震易损性的影响进行研究,并以一15层3跨钢框架结构为例进行分析。
1 钢材劣变对结构的影响
1.1 锈蚀对钢材力学性能的影响
已有研究表明钢结构在服役过程中由于受环境等因素的作用,钢材的力学性能会随服役时间的增加发生退化。因此对不同服役时间的钢结构进行地震易损性分析时需要考虑钢材力学性能劣化的影响。
史炜洲、童乐为等人[3]采用室内盐雾加速锈蚀试验模拟近海大气锈蚀环境,通过对28个不同厚度不同锈蚀程度材性试件的屈服强度进行统计分析。此外,钢材锈蚀后,屈服点和屈服平台不明显,钢材弹性模量参考H.S.Lee等人[4]提出的锈蚀钢筋弹性模量取值,得出钢材失重率与各性能指标的关系:

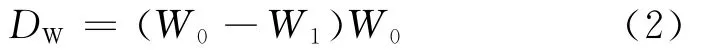
式中W0、W1分别为锈蚀前与锈蚀后试片的质量。假定钢材为均匀锈蚀,取钢材的锈蚀速率K为常数,用年锈蚀深度表示,则式(2)可改写为

式中:l0、A0分别为锈蚀前构件的截面周长与截面积,均为常数;t为锈蚀时间,单位为年。
综上,建立考虑锈蚀的钢材本构关系,作为有限元分析时材料本构关系的输入:
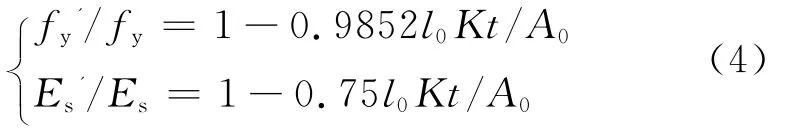
1.2 锈蚀对构件截面的影响
钢结构在环境中服役时,除了钢材力学性能会随服役时间的增加发生退化外,还会因锈蚀剥落引起截面积减小。本文依据梁彩凤[5]等通过在国内7个点17种钢的4年、8年、16年暴露试验,得出的钢的大气腐蚀的发展规律:

表1中列出了我国北京、青岛、武汉、江津、广州、琼海、万宁7个典型环境下相应的A、n值。
根据表1中的数值,以北京、琼海为例,假定钢材均匀锈蚀,可由式(5)计算得到本文钢框架采用的梁、柱截面在不同服役时间的截面面积损失率。
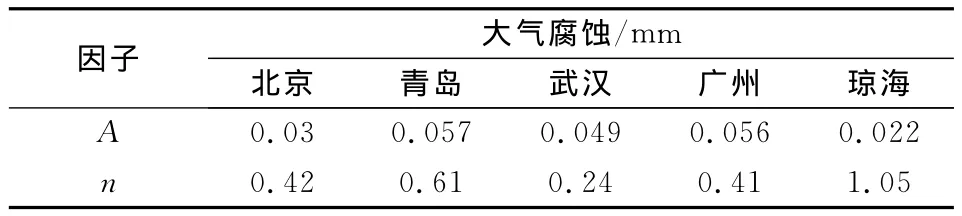
表1 典型环境下相应的A、n值Table 1 Value of A、nunder typical circumstances
由图1可知,位于两个不同区域的梁、柱截面的截面面积损失率随着结构服役时间的增加而增加。由于两个不同区域环境的差别,在算例中服役10年的位于琼海的结构的截面面积损失率最大可达7%,而服役60年则将近20%。
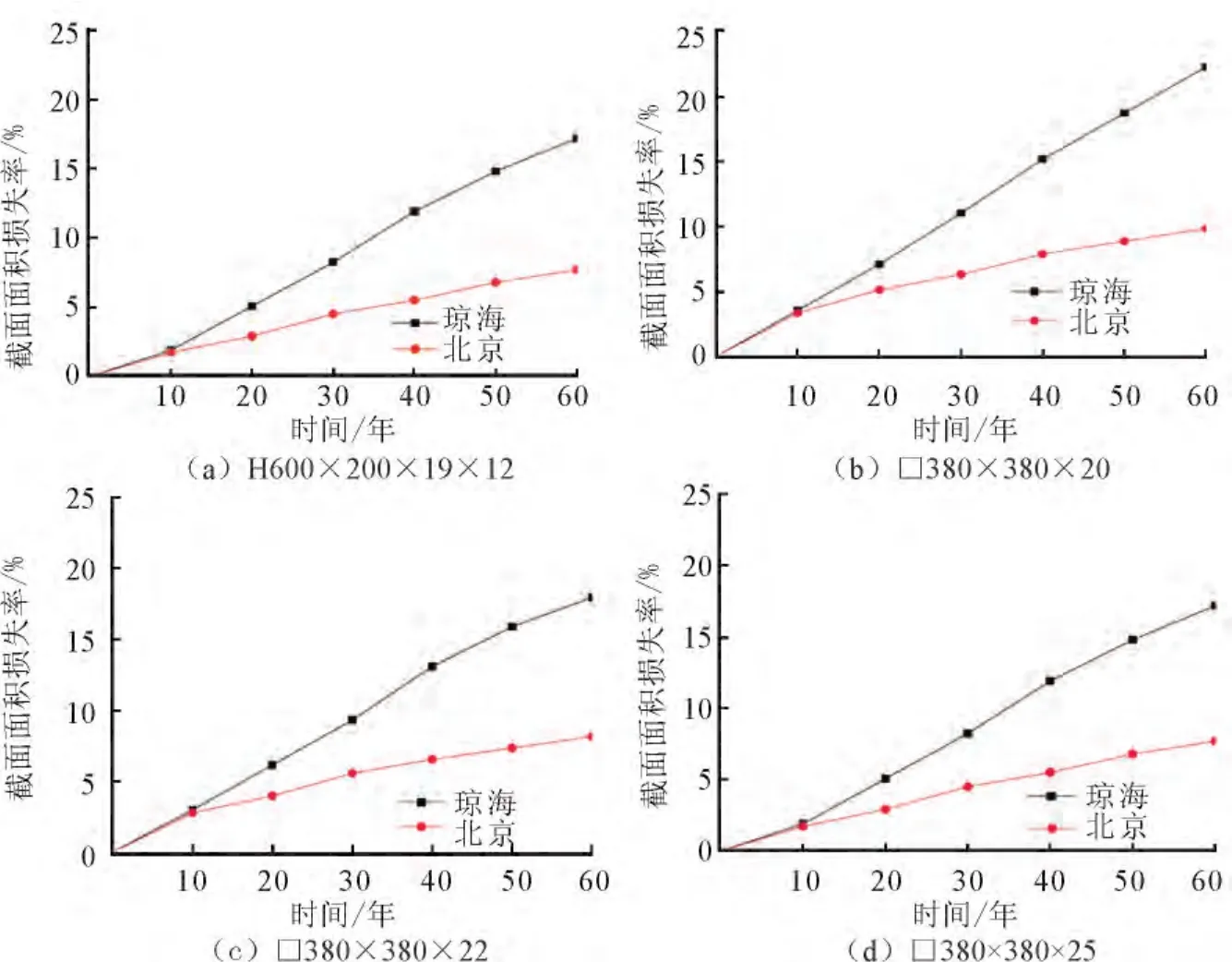
图1 本文实例中的梁柱截面面积损失率Fig.1 The loss rate of the beam and column cross-section used in the case
2 结构随机样本的形成
文献[6]指出当没有考虑结构随机性时,地震易损性曲线是带有折线性质的,而复合随机地震易损性曲线则比较平滑,离散性较小。因此,本文将考虑结构的随机性且将锈蚀对钢材力学性能及梁、柱截面的影响计入到易损性的分析中来。
根据蒙特卡洛(Monte Carlo)随机抽样,若随机变量服从正态分布,则由式(6)产生随机样本:

式中:x为服从正态分布的随机变量;μ、σ为随机变量的均值和标准差;Ri为[0,1]的伪随机数。对数正态分布的随机变量可通过与正态分布变量的对应关系产生,由式(7)得到服从对数正态分布的样本y:

不同服役时间的结构随机样本可由式(4)、表2及式(6)、(7)表示成
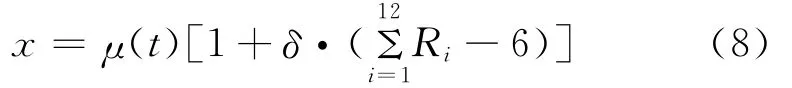
式中:μ(t)为服役时间t时的随机变量均值;δ为随机变量的变异系数。
利用Matlab程序中的随机数生成器,生成结构随机样本。

表2 算例结构参数的统计特征Table 2 Statistical characteristics of the structural parameters
3 考虑钢材锈蚀的地震易损性模型
文献[7]指出地震需求D的中位值mD和地震动IM之间一般服从幂指数回归关系,且结构的地震需求D与地震能力C均服从对数正态分布:
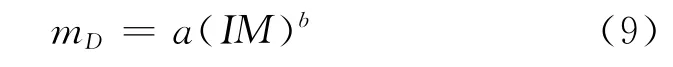
在考虑结构服役时间对地震易损性的影响时,式(9)的拟合参数a、b及概率地震需求分析的对数标准差βD将变为时间t的函数。因此,式(9)可写为

式中:a(t)、b(t)是考虑服役时间因素的地震需求mD的拟合参数。
美国北岭地震和日本阪神地震震害显示,梁柱焊接钢结构在地震作用下易发生脆性破坏,而我国既有钢结构大多采用梁柱焊接的节点形式且钢材锈蚀增大结构发生脆性破坏的概率。因此,为简化计算方法和减小计算量,采用Cornell研究建议[8],对易发生脆性破坏的钢结构取b=1,式(10)可改写为
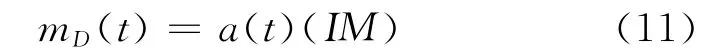
地震易损性从概率的角度定量地描述结构在不同强度地震作用下发生各种不同破坏状态的概率[9],则结构特定阶段的失效概率平Pf可由式(12)确定:

为得到结构在设计使用期限内任意服役时间t对应的4种不同破坏状态的易损性曲线,有必要建立结构连续失效概率函数。本文对地震需求拟合参数a(t)建立与时间t(0年、15年、30年、45年、60年)的对应关系并进行拟合得到随时间的变化规律,将式(11)代入式(12),则得到考虑钢材锈蚀的钢结构特定阶段的失效概率:
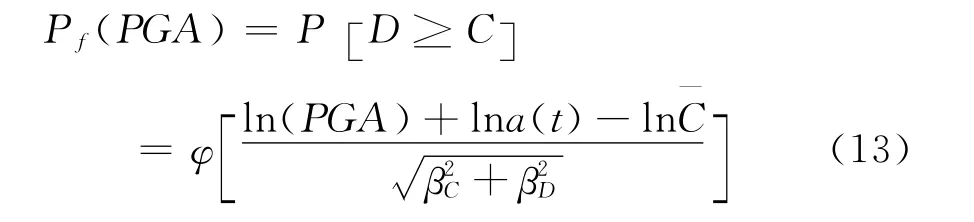
式(13)以时间t、地震动强度PGA为自变量,结构失效概率Pf为因变量的函数。因此,式(13)是以易损性曲面的形式表达结构在不同时间不同地震动强度下不同破坏状态的概率,为简化计算假定结构的能力与需求标准差βC与βD与时间无关。
4 算例分析
4.1 地震波选取
依据文献[9-10]的选波原则在美国太平洋地震研究中心(PEER)的强震数据库[11]中选取20条地震动记录作为输入,所选地震波见表3:

表3 选用的地震波Table 3 Ground motion records used in the study
4.2 计算模型
本文选取15层3跨钢框架,结构抗震设防烈度为Ⅷ度,按Ⅱ类场地土及近震条件考虑。由于结构平面布置规则,选取一榀框架利用SeismoStruct有限元分析软件分析。梁、柱截面尺寸见表4。

表4 15层3跨钢框架梁柱截面Table 4 Beam and column cross-section of steel frame
4.3 结果分析
地震易损性分析分为三个部分:结构的能力计算、结构的地震需求计算以及地震易损性曲线的形成[12]。本文在分析时以PGA为地震动强度指标,以最大层间位移角θmax为地震需求指标。
依据文献[7,13]将结构极限状态分为:基本完好、轻微破坏、中等破坏、严重破坏以及毁坏五个等级。采用Pushover对结构随机样本分析确定不同极限状态结构最大层间位移角均值¯C和结构承载力的对数标准差βc。定义结构在不同破坏状态地震易损性分析采用的极限状态值,见表5。

表5 不同性态水平的层间位移角限值Table 5 Story drift limit values in different levels
利用IDA分析方法对结构随机样本进行分析并对分析结果进行对数线性拟合,得到算例结构在5个不同时间的结构反应均值¯D的拟合关系:

式中:下标数字表示结构服役时间分别为0年、15年、30年、45年、60年;其中b值取1后,式(14)拟合相关系数 R 分别是 0.920、0.918、0.912、0.923、0.916。
为得到结构在设计使用期限内连续的4种不同破坏状态的易损性曲面。本文对不同时间的地震需求拟合参数a(t)与时间t进行拟合:

表6 不同服役时间的a(t)/a0 值Table 6 Values of a(t)/a0in different service times
本文根据表6中数值随时间变化规律选取指数关系拟合,拟合结果如式(15):
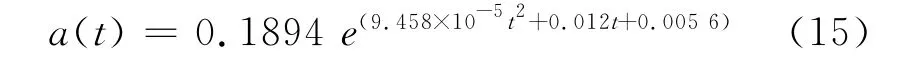
将式(15)代入式(13)即可得到结构在不同服役时间五种破坏状态下的易损性曲面,如图2所示。
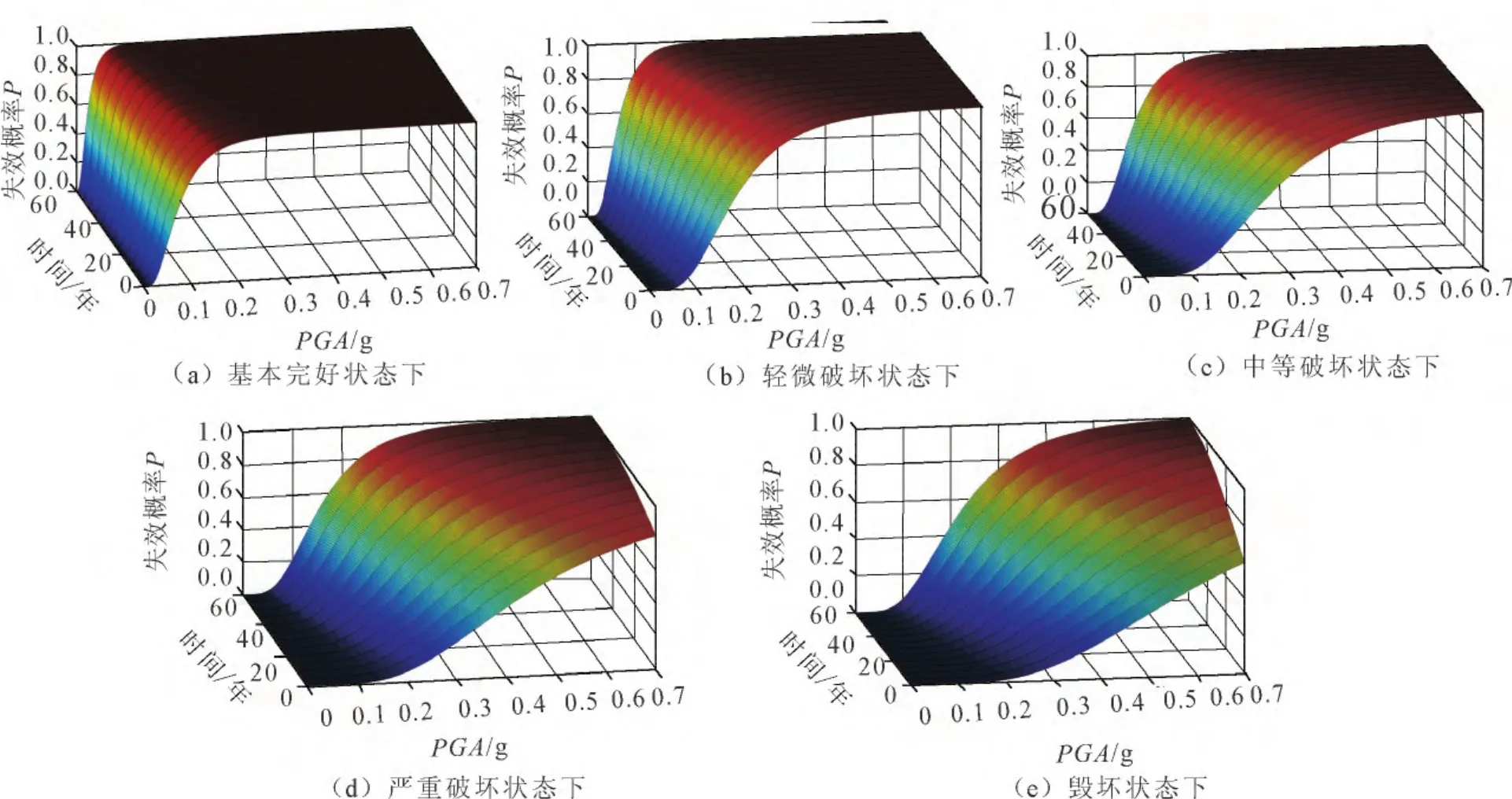
图2 考虑锈蚀的钢结构地震易损性曲面Fig.2 The seismic fragility surfaces of the steel frame consider corrosion
由图2可知,由于钢材锈蚀导致结构整体承载能力与延性下降,5种破坏状态的失效概率都随着结构服役时间的增加而增加。在算例中初始服役与服役60年的结构的失效概率,在中等破坏、严重破坏及毁坏状态最大降幅分别将近10%、30%、50%。因此在进行钢框架结构设计时需要考虑钢材锈蚀对结构地震风险增加的影响。
5 结语
本文在结合已有钢材随时间劣变规律的基础上,利用蒙塔卡罗随机抽样建立结构随机样本,采用IDA与pushover方法进行分析,重新建立了结构的地震需求与能力模型并计算得到了钢结构在服役0年、15年、30年、45年、60年的地震易损性曲面。本文的研究成果可为钢框架结构的全寿命设计、既有建筑结构的运营以及地震风险评估等提供理论依据。
(References)
[1]陈露,徐善华,孔正义,等.有限元在腐蚀输电塔安全评定中的应用[J].钢结构,2010,25(6):76-79.CHEN Lu,XU Shan-hua,KONG Zheng-yi,et al.Application of Finite Element Method to Safety Assessment on Corroded Transmission Towers[J].Steel Construction,2010,25(6):76-79.(in Chinese)
[2]Betro L,Vitaliani R,Saetta A,et al.Seismic Assessment of Existing RC Structure Affected by Degradation Phenomena[J].Structural Safety,2009,31(4):284-285.
[3]史炜洲.钢材腐蚀对住宅钢结构性能影响的研究与评估[D].上海:同济大学,2009:46-62.SHI Wei-zhou.Research and Evaluation on Influence of Corrosion on Behavior of Building for Steel Frame[D].Shanghai:Tongji University,2009:46-62.(in Chinese)
[4]Lee H S,Noguchi T,Tomosawa F.FEM Analysis for Structure Performance of Deteriorated RC Structures Due to Rebar Corrosion[C]//Prodceedings of the International Concrete Under Several Conditions.1998.
[5]梁彩凤,候文泰.碳钢及低合金钢16年大气暴露腐蚀研究[J].中国腐蚀与防护学报,2005,25(1):3-6.LIANG Cai-feng,HOU Wen-tai.Sixteen-year Atmospheric Corrosion Exposure Study of Steel[J].Journal of Chinese Society for Corrosion and Protection,2005,25(1):3-6.(in Chinese)
[6]冯清海.特大桥梁地震易损性与地震风险概率分析[D].上海:同济大学,2008.Feng Qing-hai.Seismic Vulnerability and Seismic Risk Probabilistic Analysis for Large Bridge[D].Shanghai:Tongji University,2008.(in Chinese)
[7]王丹丹.钢框架结构的地震易损性及概率风险分析[D].哈尔滨:哈尔滨工业大学,2006.WANG Dan-dan.Seismic Fragility Analysis and Probabilistic Risk Analysis of Steel Frame Structures[D].Harbin:Harbin Institute of Technology University,2006.(in Chinese)
[8]Cornell C A,Jalayer F,Hamburger R O,et al.Probabilistic Basis for 2000SAC Federal Emergency Management Agency Steel Moment Frame Guidelines[J].Struct.Eng.,2002,128(4):526-533.
[9]徐龙河,单旭,李忠献.强震下钢框架结构易损性分析及优化设计[J].工程力学,2013,30(1):175-176.XU Long-he,SHAN Xu,LI Zhong-xian.Vulnerability Analysis and Optimization Design for Steel Frame Structure Under Strong Earthquakes[J].Engineering Mechanics,2013,30(1):175-176.(in Chinese)
[10]吴小峰,孙启国,狄杰建,等.抗震分析反应谱法和时程分析法数值仿真比较[J].西北地震学报,2011,33(3):276-278.WU Xiao-feng,SUN Qi-guo,DI Jie-jian,et al.A Numerical Simulation Comparison Between Response Spectrum Analysis and Time History Analysis[J].Northwestern Seismological Journal,2011,33(3):276-278.(in Chinese)
[11]Pacific Earthquake Engineering Research Center.PEER Strong Motion Database[DB/OL].http://peer.Berkeley.edu//smcat.
[12]庞于涛,袁万城,党新志,等.考虑材料劣变过程的桥梁地震易损性分析[J].同济大学学报,2013,41(3):348-354.PANG Yu-tao,YUAN Wan-cheng,DANG Xin-zhi,et al.Stochastic Fragility Analysis of Bridges with a Consideration of Material Deterioration[J].Journal of Tongji University,2013,41(3):348-354.(in Chinese)
[13]刘晶波,王文辉,赵东东,等.循环往复加载的地下结构分析方法及其在地震损伤分析中的应用[J].地震工程学报,2013,35(1):21-23.LIU Jing-bo,WANG Wen-hui,ZHAO Dong-dong,et al.Pushover Analysis Method of Underground Structures Under Reversal Load and Its Application in Seismic Damage Analysis[J].China Earthquake Engineering Journal,2013,35(1):21-23.(in Chinese)

