铁路空心墩抗震性能的拟静力试验研究①
韩国庆,司大鹏
(中铁二院工程集团有限责任公司,四川 成都 610031)
0 引言
铁路桥梁当墩高大于30m时由于实体截面墩身混凝土圬工数量很大(双线桥梁时尤为突出),墩身、基础设计均不经济,桥墩通常采用空心截面[1]。拟静力试验方法通常被广泛应用于结构或构件的承载力、刚度、变形能力、耗能能力和损伤特征等方面的研究。尽管国内外已对实体桥墩有较多的拟静力试验研究,并取得了很多成果[2-6],但空心墩与实体墩在截面的纵筋与箍筋布置方面有很大的差异,塑性铰发生机理也不一样,其成果能否直接用于铁路空心墩尚须研究。而采用缩型模型进行模拟试验目前效果比较好的方法。
针对铁路桥梁常用的空心圆端形截面桥墩,本文采用拟静力试验研究其截面合理配筋、地震破坏模式、单调加载的骨架曲线、反复荷载作用下的滞回规则及塑性铰区域长度,为铁路空心墩的抗震设计提供依据。
1 模型设计与制作
1.1 相似关系
为了验证现行设计的配筋是否合理,获得研究使用的基础数据,为理论模型和计算分析方法的建立提供依据,以大理—瑞丽铁路漾濞1号桥的8#桥墩为模型原型(图1(a)),制作了三个圆端型空心墩缩尺模型(图1(b)、(c)),模型的配筋见图2。

图1 大瑞铁路漾濞1号特大桥8#桥墩和模型(单位:cm)Fig.1 No.8pier of No.1Yangbi bridge on Dali-Ruili railway and its models(unit:cm)
漾濞1号桥的8#桥墩,墩高为38cm,墩身的内、外侧坡度分别为66∶1和40∶1,墩壁厚在0.4~0.67m之间。墩身的混凝土圬工量为358.45 m3、重为8961.3kN。纵向钢筋配筋率为0.8%,体积配箍率为0.9%,箍筋间距为10cm。综合各方面的因素,取截面尺寸的相似比为1∶5,根据相似原理[7]给出模型与参考原型主要物理量的相似系数如表1所示。
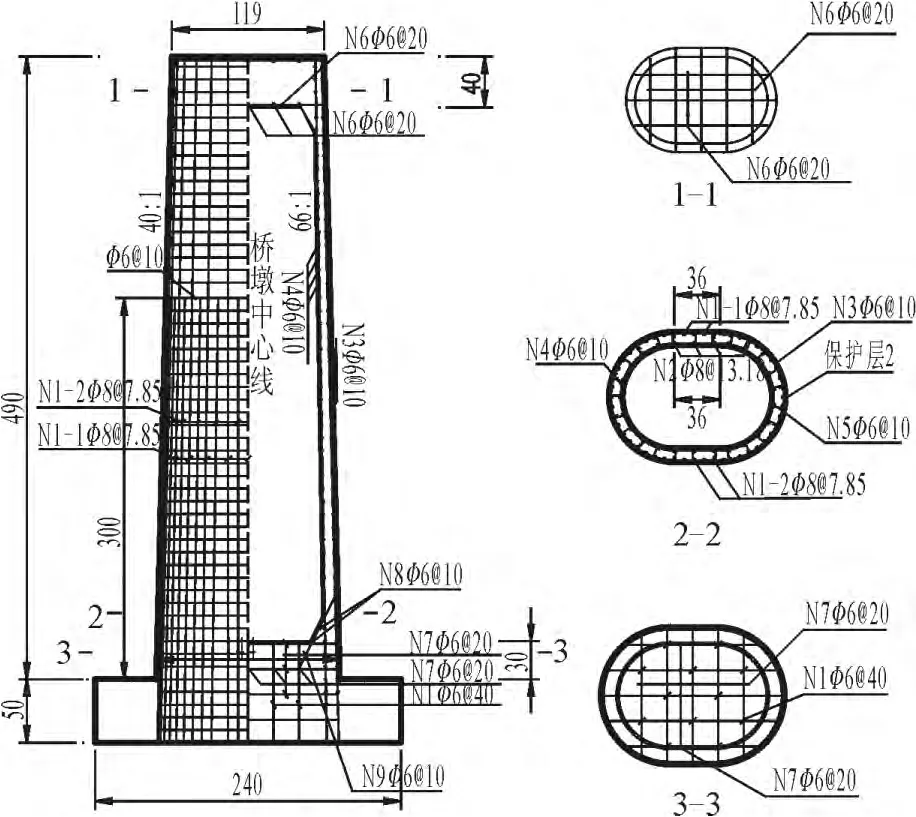
图2 模型桥墩的配筋Fig.2 Reinforcement arrangement of the pier model
1.2 模型材料与制作
模型桥墩采用C30混凝土。主筋为φ8mm的HRB335级钢筋内外双层布置,外层等距布置50根、内层等距布置25根,沿墩身等间距10cm布置φ6mm的HRB级箍筋。模型竖向荷载主要包括:墩身自重、梁部重量以及二期恒载。根据相似原理,墩顶竖向荷载为878kN。制作完成的模型桥墩及加载系统见图3。
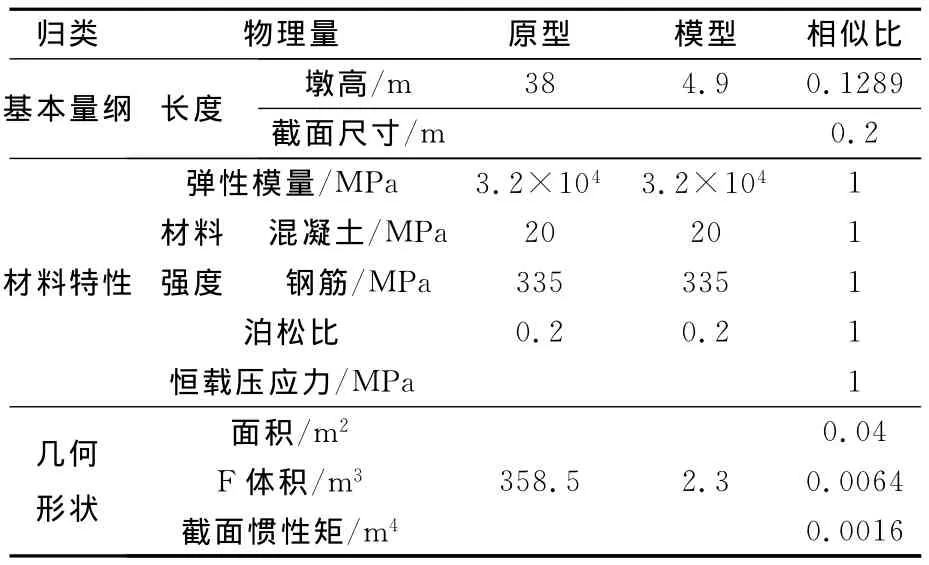
表1 模型设计各参数的相似系数Table 1 The similarity coefficients of each parameter in the model

图3 模型外观照片Fig.3 Photos of the completed pier model
2 模型试验现象及结果
2.1 试验现象
竖向荷载由千斤顶一次施加到预定值878kN,墩身开裂前逐级施加水平力,开裂后改成位移加载。模型墩底第一条裂缝出现在距离墩底15~20cm处,这一部位是模型的实体段与空心段交界部位。裂缝的形成与扩展过程如下:
(1)墩底实体段与空心段交界处出现第一条裂缝;(2)紧接着在距墩底100cm左右的地方出现裂缝;(3)随着荷载的加大在50~100cm范围的墩身出现裂缝群,裂缝比较密集,每条裂缝间隔在10~15cm左右,与此同时墩身南北两侧100cm以下裂缝发展迅速,并逐渐贯通形成环状裂缝;(4)随着荷载的持续增大墩身下部200cm以下范围内裂缝以10~15cm左右的间距发展,并在100cm以下实体段以上部分裂缝密集发展,环状近似水平裂缝之间开始出现竖向裂缝并逐渐在相邻两环状裂缝之间贯通,墩身各横向裂缝互相贯通呈大面积发展趋势,混凝土开始剥落,出现了箍筋的外鼓、纵筋的拉断和屈服等破坏现象;(5)试验模型逐渐出现延性破坏,主要体现为纵向主筋的拉断和混凝土的压碎,具有明显的塑性铰区域。
根据试验现象发现三个模型的裂缝发展规律基本上比较接近,模型二的墩身裂缝如图4。
模型桥墩(模型二)的塑性铰区混凝土压碎及受拉钢筋的屈服、拉断破坏形式见图5。

图4 模型桥墩及加载系统Fig.4 Schematic diagram of the pier craks on No.2model

图5 模型二的混凝土、钢筋破坏情况Fig.5 The damage of concrete and reinforcement of No.2model
从模型的塑性铰区域破坏现象中不难得到,虽然破坏形态基本上呈现延性破坏形态,但塑性铰区域混凝土剥落到一定程度后,也出现了部分受拉钢筋拉断的现象,这就表明设计中采用的纵向钢筋配筋率(0.8%)略显不足,根据美国等相应规范中最小配筋率的规定[8],建议该铁路空心墩的纵向主筋配筋率为1.0%。此外,在本试验中还观察到当墩身混凝土保护层剥落后,箍筋对核心混凝土起到了预想的侧向约束作用,且尚未出现拉断破坏现象,这表明现有墩身箍筋量(体积配箍率为0.9%)和设置方式是合理的。
根据三个模型的试验情况,将其裂缝的分布范围和发展规律列于表2,并将试验模型的塑性铰区域的长度和桥墩受力方向的截面长度一并列出。
2.2 试验结果分析
试验结果包括单调加载的骨架曲线合塑性铰区域长度、墩顶的力—位移滞回曲线,详见图6(a)、(b)。
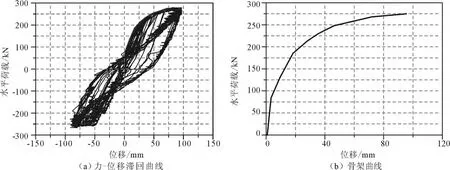
图6 模型二的力-位移滞回曲线和骨架曲线Fig.6 The force-displacement hysteresis curve and skeleton curve of No.2model

表2 模型桥墩的试验塑性铰区长度Table 2 The lengths of plastic hinge of the pier models
由表2可得到,模型试验的塑性铰区域长度Lp与墩底受力方向截面尺寸b比较接近,故建议空心墩塑性铰区域长度的近似计算公式为

上式与日本铁道抗震设计规范给出的公式一致。
3 模型试验的数值模拟
采用Opensees分析软件中的纤维单元建立数值分析模型,计算分析时墩身保护层混凝土采用无约束模型,核心混凝土采用 Mander模型[9],输入表1中的材料强度。数值模拟得到的单调加载骨架曲线与试验曲线的对比如图7(a)。Takeda三线性滞回模型的数值模拟与试验曲线的对比见图7(b)。
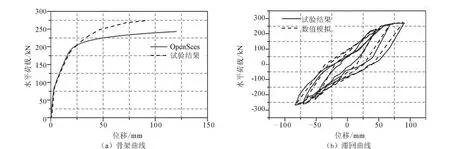
图7 模拟骨架曲线和滞回曲线与试验曲线的对比Fig.7 Comparisons of model skeleton curve with test skeleton curve and model hysteresis curve with test hysteresis curve
由图7可知,建立的数值分析模型能够较好地模拟该铁路空心桥墩的骨架曲线,Takeda三线性滞回模型也可以较好地模拟空心桥墩的滞回特性。
4 结论
(1)模型桥墩的破坏特征主要体现为混凝土的压碎,有明显的塑性铰区域,呈现延性破坏。
(2)模型桥墩的塑性铰区域长度LP与模型墩底受力方向截面尺寸b相近,建议空心桥墩的塑性铰区域长度按照日本铁道抗震设计规范的公式计算。
(3)现有纵向钢筋配筋率(0.8%)略为不足,参考美国加州及我国台湾桥梁抗震设计规范中最小配筋率的规定,建议该墩的纵向钢筋配筋率取值为1.0%,现有箍筋量(体积配箍率为0.9%)与设置方式合理。
(4)结合试验结果的对比分析,得到Takeda三线性滞回模型可以较好地模拟空心墩的滞回特性。
(References)
[1]陈慧.铁路桥梁圆端形空心墩的设计[J].铁道标准设计,2009,(4):77-79.CHEN Hui.Design of Railway Bridge of Circular Hollow Pier[J].Railway Standard Design,2009,(4):77-79.(in Chinese)
[2]刘庆华,阎贵平,陈英俊.低配筋混凝土桥墩抗震性能的实验研究[J].北方交通大学学报,1996,20(5):517-521.LIU Qing-hua,YAN Gui-ping,CHEN Ying-jun.Experimental Studies on Seismic Behaviour of Reinforced Concrete Bridge Piers[J].Journal of Northern Jiaotong University,1996,20(5):517-521.(in Chinese)
[3]孙卓,李建中,闫贵平,等.钢筋混凝土单柱式桥墩抗震性能试验研究[J].同济大学学报,2006,34(2):160-164.SUN Zhuo,LI Jian-zhong,YAN Gui-ping,et al.Experimental Study on Seismic Performance of Reinforced Concrete One-Column Bridge Piers[J].Journal of Tongji University:Natural Science,2006,34(2):160-164.(in Chinese)
[4]夏修身.铁路连续梁拱组合桥基于摩擦摆支座的减隔震研究[J].西北地震学报,2012,34(4):350-354.XIA Xiu-shen.Seismic Isolation of Combined System of Continuous Girder-arch Railway Bridge Using Friction Pendulum Bearing[J].Northwestern Seismological Journal,2012,34(4):350-354.(in Chinese)
[5]李贵乾.钢筋混凝土桥墩抗震性能试验研究及数值分析[D].重庆:重庆交通大学,2010.LI Gui-qian.Experimental Study and Numerical Analysis on Seismic Performance of Reinforced Concrete Bridge Columns[D].Chongqing:Chongqing Jiaotong University,2010.(in Chinese)
[6]司炳君,李宏男,王东升,等.基于位移设计钢筋混凝土桥墩抗震性能试验研究(Ⅰ):拟静力试验[J].地震工程与工程振动,2008,28(l):123-129.SI Bing-jun,LI Hong-nan,WANG Dong-sheng,et al.Experimental Evaluation of the Seismic Performance of Reinforced Concrete Bridge Piers Designed on the Basis of Displacement(Ⅰ):Quasi-static Test[J].Journal of Earthquake Engineering and Engineering Vibration,2008,28(1):123-129.(in Chinese)
[7]朱伯龙.结构抗震试验[M].北京:地震出版社,1989.ZHU Bo-long.Structures Earthquake Resisting Test[M].Beijing:Seismological Press,1989.(in Chinese)
[8]Caltrans Seismic Design Criteria Version 1.4[S].2006.
[9]张永亮,孙建飞,徐家林.高速铁路大跨连续梁桥地震反应分析及抗震校核[J].地震工程学报,2013,35(2):226-231.ZHANG Yong-liang,SUN Jian-fei,XU Jia-lin.Analysis of Seismic Response and Seismic Checking in a Long-span Continuous Beam Bridge on a High-speed Railway[J].China Earthquake Engineering Journal,2013,35(2):226-231.(in Chinese)

