旧采区域内遗留煤柱及空巷稳定性分析
郭晓彦
(西山煤电(集团)公司 屯兰矿,山西 太原 030200)
1 旧采区概况
山西忻州神达望田煤业有限公司位于保德县城东南6 km处,由保德县望田煤业有限公司、保德县德能煤业有限公司、保德县德源煤炭有限责任公司及新增区整合而成。望田煤业8#煤属于厚煤层,兼并重组前由于受自身装备水平以及开采技术条件的限制,一直使用反复送巷、扩帮的巷柱式开采法,在井下遗留大量煤柱,对煤炭资源造成的浪费,导致井田内8#煤层的完整性受到严重破坏,在底煤中会形成“空巷-煤柱-空巷”结构,遗留煤柱尺寸一般约为8~20 m,空巷跨度一般在2~8 m。残留的空巷上方顶煤搭接在煤柱上方呈空顶状态,在旧采区进行残采时,判断空巷之间的煤柱以及空巷上方顶板是否稳定,即判断煤柱保持稳定的最小宽度以及空巷的最大跨度是有必要的。
2 旧采区空巷顶板稳定性分析
井下空巷问题一直是影响工作面安全回采的难题,而旧采区残采工作面常会遇到工作面过空巷情况。由于旧采区经过长时间搁置以及受矿山压力作用,需要对旧采区内空巷的稳定性做出判断。空巷顶板的完整性对支护方案的选择以及安全技术措施的制定起着重要作用。通过建立空巷顶板力学模型,计算出望田煤业空巷顶板的极限跨度,进而从理论上预测旧采区内空巷顶板的完整情况。
梁的理论是计算与分析巷道和工作面极限悬露跨度的重要理论,也是应用较为广泛的理论之一,故选用该理论计算厚煤层空巷上方的厚顶煤的极限跨距,两端固支梁受力分析见图1。

M—该点所在端面的弯矩 y—该点离中性轴的距离 Iz—对称中性轴的断面距
根据材料力学中两端固支梁受力计算公式可以求得顶煤内任意一点的正应力σ为:
(1)

两端固支梁的最大弯矩发生在其两边端部,则最大拉应力σmax为:
σmax=qL2/2h2
(2)
当最大拉应力大于等于该处的抗拉极限强度时,顶煤将在此处发生拉裂,从而可求得顶煤发生断裂时的极限跨度L极:

(3)
式中:
RT—顶煤抗拉强度;
q—顶煤自重与上方岩层产生载荷的总和。
顶煤在受自重作用影响的同时,还要受到其上方岩层间相互作用而产生的载荷,式(3)中的q可依据组合梁理论得出载荷计算公式:
(4)
式中:
h1,h2…hn—各岩层厚度,m;
E1,E2…En—各岩层弹性模量, GPa;
γ1,γ2…γn—各岩层体积力,kN/m3。
当利用式(4)计算得到(qn+1)1<(qn)1时,则以(qn)1作为作用于顶煤所承受的载荷,进而可以将(qn)1代入式(3),从而可以求出空巷上方顶煤的最大跨度。望田煤业8#煤层及其上方岩层力学参数见表1。
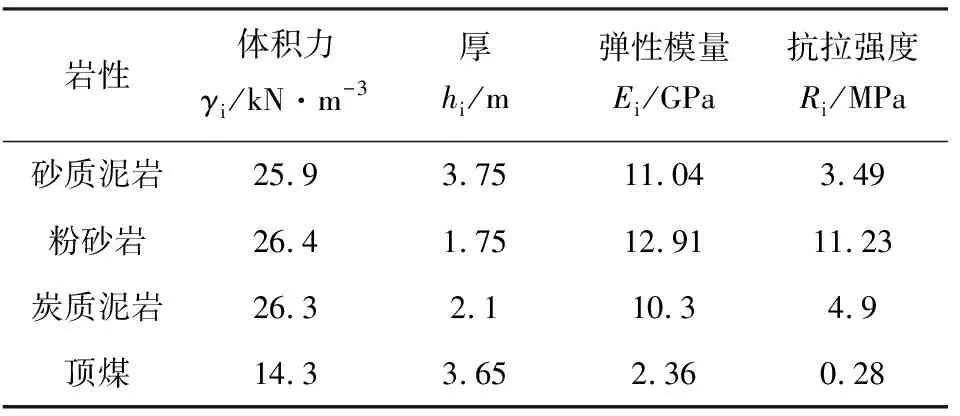
表1 煤岩层力学参数表
将表1中各煤岩层力学参数带入式(4),可得:
空巷上方顶煤本身的载荷q1为:
q1=γh1=14.3×3.65=52.2 kPa
考虑空巷上方第2层对顶煤的作用,进而可求得载荷为:
考虑空巷上方第3层对顶煤的作用,进而可求得载荷为:
考虑空巷上方第4层对顶煤的作用,进而可求得载荷为:
则:(q4)1<(q3)1
在残采工作面前方仅有一条空巷存在或空巷之间相隔较远时,可按固支梁模型计算空巷顶板跨度。将顶煤抗拉强度和计算出的顶煤所受载荷代入式(3)可求出顶煤的极限跨距为:L极=10.8 m。

3 空巷群之间煤柱的稳定性分析
望田煤业8#煤层为厚煤层,旧巷柱式采煤法沿煤层底板扩帮开采后,在底煤中遗留的煤柱支撑着采空区上覆煤岩层结构,形成“空巷-煤柱-空巷”区,也称为空巷群,在残煤开采工作面回采过程中极有可能会遇到空巷群。如果煤柱有足够的稳定性,可以保证残采工作面推进过程中空巷带的稳定性,进而保证顺利推进;如果残留煤柱不能有效地支撑上覆岩层,则在开采以前或推进过程中,煤柱可能失稳破坏导致空巷带破坏造成工作面难以推进甚至造成事故伤害。为此,残采工作面能否安全顺利通过空巷带,空巷之间煤柱的稳定性起着关键性影响。通过建立力学模型以及理论分析和计算,从而初步判断望田煤业8#煤层空巷群之间煤柱的稳定性。
3.1 煤柱分析
煤柱体自开采后形成直到发生破裂失稳是一种量变到质变的积累过程,在不同时期作用于煤柱体上的应力分布不同。
1) 未破坏前应力分布。
未开采以前煤层保持完整状态,煤体所承受载荷为上覆煤岩体的自重,呈均匀分布,此时为原岩应力状态,见图2。

图2 实体煤状态受力情况图
2) 煤柱受力分析。
准备工作就绪后,我们利用班会课给大家公布了“先锋车站”的行事原则,也任命了小刘的职务,最后,由小刘宣布“车站”正式成立。先锋车站的故事就这样拉开了帷幕。
实现残采工作面的安全顺利推进,首先要确定切眼前方空巷群间煤柱的稳定能力,而遗留煤柱的宽度是影响其稳定能力的关键因素,稳定煤柱中所受支承压力情况见图3。

Ⅰ—破裂区 Ⅱ—塑性区 Ⅲ—弹性核区
由图3可知,在煤柱两侧边缘部位容易形成集中应力,由于矿山压力的作用,一般将煤柱划分为三区,从煤柱边缘向其内部依次划分为破裂区、塑性区和弹性区。
3.2 稳定煤柱宽度
采用在计算煤柱极限弹性区时能够将煤柱自身的应变软化性质以及主应力的影响考虑在内的且更符合厚煤层中巷道的围岩变形特征的扩展SMP准则,来计算煤柱极限弹性区宽度,扩展SMP准则在符合Mohr-Coulomb屈服准则的同时,不仅克服了偏平面中Mohr-Coulomb准则的奇异性,而且解决了Drucker-Prager准则的矿压强度相等性问题。
Matsuoka在20世纪90年代对只适合无黏性材料的SMP准则做出了修改,在主应力表达式中引入了黏结应力σ0(σ0=C·cotφ,其中c为黏聚力,φ为内摩擦角),使之能适用于c-φ材料,称为扩展SMP准则,则基于扩展SMP准则的平面应变条件下的黏性材料的破坏准则是:
(5)
两条空巷间的煤柱所受的支承压力基本上可以看成对称分布,故可取弹性区的一半进行研究,煤柱左半部分弹性核区受力情况见图4。

图4 煤柱中部左端支承应力分布图
在实际生产过程中,由于井下煤层的埋藏深度远远大于煤层的厚度,可将水平应力σx近似的看成是均匀分布的,将垂直应力σy沿着煤层厚度的方向近似看成是不发生变化的。根据以上假设,应用弹塑性力学中最大主应力公式及应力函数,可得到弹性区内任意一点的最小与最大主应力。由图4可知,煤柱弹性区在y=M/2,x=0处分别取得最小与最大主应力,计算公式分别为:
(6)
(7)
式中:
η—侧压系数;
M—煤柱高度,m;
μ—泊松比;
φ—内摩擦角,(°);
C—黏聚力,MPa;
K2—应力集中系数,取1~3。
将公式(6)及(7)代入公式(5)中,可得扩展SMP准则下煤柱弹性区宽度计算公式,弹性区左半部分长度x0为:
x0=
(8)
式中:
Q=8 tan2φ+9
η=μ/(1-μ)
σ0=Ccotφ
望田煤业残采工作面的埋藏深度在200 m左右,容重γ为2.5×104N/m3,实测煤的物理力学参数:3#煤的抗压强度为7.78 MPa,黏聚力为1.2 MPa,泊松比为0.27,内摩擦角为37°,将以上各参数代入式(7)可以得出:x0=1.71 m。依据理论计算与实测分析,煤柱稳定时的弹性核区率ρ=65%,从而可以求出煤柱宽度B=2x0/ρ=5.31 m,取5.5 m。根据现场调查和原小煤矿技术资料分析,旧采区内遗留煤柱尺寸多在6~20 m,从而可知残采工作面前方空巷群之间的煤柱基本处于稳定状态。
4 结 论
1) 根据弹性梁理论对旧采区空巷极限跨度进行计算,残采工作面遇到单一空巷时,空巷最大跨度为10.8 m。
2) 残采工作面遇到多条相邻空巷时,可以看成简支梁模型,空巷最大跨度为8.8 m。
3) 运用扩展SMP准则对空巷之间煤柱稳定性进行分析,巷间煤柱保持稳定的最小宽度为5.5 m。
参 考 文 献
[1]贺广零,黎都春.采空区煤柱一顶板系统失稳的力学分析[J].煤炭学报,2007(9):898-901.
[2]翟新献,钱鸣高,李化敏,等.小煤矿复采煤柱塑性区特征及采准巷道支护技术[J].岩石力学与工程学报,2004,23(24):37-38.
[3]邹友峰,柴华彬.我国条带煤柱稳定性研究现状及存在问题[J].采矿与安全工程学报,2006,23(2): 141-145.
[4]蒋 坤,家 林,朱卫兵,等.条带采宽对地表沉陷影响的数值模拟研究[J].矿山测量,2005(4):51-53.

