充液圆槽中单极声波仪器响应数值模拟与分析*
何 晓陈 浩 王秀明
(中国科学院声学研究所 声场声信息国家重点实验室 北京 100190)
1 引言
为了对声波测井仪器进行测试和标定,石油工业界采用的传统方法是将仪器放置在有限厚度的轴对称径向分层的人工模型井中,通过接收和分析井中的声波响应信号实现声速刻度以及对发射和接收换能器工作状态的检测。针对这种充液轴对称模型中的声传播规律和波场特征,近几十年来国内外许多学者进行了大量的理论和实验研究。Gazis[1-2]首次研究了具有自由表面的薄壁空心圆管中波的传播,并通过求取波动方程的特征根获得了沿圆管轴向传播的模式波频散曲线。应用同样的研究方法 Sinha等[3]和 Plona等[4]进一步揭示了圆柱管在液体载荷作用下的各阶泄漏模式波的频散和衰减特征,并与声学实验测量结果进行了对比。Wang和Dodds[5]则采用实轴积分法计算了径向多层模型中的管内波场,着重讨论了圆管厚度对全波特征的影响以及分析了模式波的径向探测深度。Aristégui等[6]通过理论分析和实验测量揭示了载荷流体性质对圆管模式波频散和衰减的影响。在前人研究成果的推动下,在充液有限厚圆管模型中标定声速测井仪器及对换能器工作状态进行检测的方法得到了不断完善,并且已逐渐形成了单极子声速测井仪器刻度技术的行业标准和规范(如“声速测井仪器刻度装置技术规范”,中华人民共和国石油天然气行业标准,SY/T6492-2000)。
然而,利用轴对称圆管进行仪器标定和检测存在着一些固有的不足。一方面,在测井仪器的几何特征(比如源距约为3~4 m,仪器总长约10 m)决定了竖直放置的充液圆管需要有很大的轴向尺度,这既对室内测量时的场地空间和相关辅助设施提出了严格要求,也非常不便于在测井现场对仪器作快速检测;另一方面,由于在轴对称模型情况下换能器不能激励反映各向异性的偶极子交叉分量响应,封闭圆管不利于对交叉偶极测井仪器进行全面检测、或对仪器进行各向异性标定。因此近年来测井工程师们提出了在水平放置的具有弧形截面的开口载液圆槽中进行仪器检测和标定的设想并得到了推广。相对于传统的轴对称圆管仪器检测方法,这种在水平圆槽中的仪器测试手段更快捷简便且易于实施;同时在非轴对称结构中偶极声波仪器能激发出交叉分量响应,可适用于对偶极子仪器的检测与标定。目前,针对这种充液开口弧形圆槽中声波传播的规律国内外尚未有文献报道,利用水平圆槽进行仪器标定和检测的实际工作仍处于缺乏理论基础的摸索阶段,远未能形成统一的操作规范和检测标准。
由于流体-圆槽模型为非轴对称结构,在分析轴对称声波导时常用的求解波动方程的解析算法将不再有效。在本文中为了获得弧形截面圆槽中声波测井的声场数值模拟结果,我们将采用柱坐标系下三维有限差分算法,考察声波测井仪器在这种非轴对称模型中的波形响应,并分析圆槽几何尺寸和仪器参数对接收器信号的影响,为今后声波测井仪器在非轴对称圆管系中的刻度和检测方案的确立提供必要的理论依据。在本文中我们的研究对象是充液圆槽中单极子声波的响应,在后续论文中将会继续展示偶极仪器波场的数值模拟结果。
2 模型及数值算法
在本研究中,我们采用的圆槽是由轴对称圆管截掉一个角度为β的扇形区域而制成的弧形截面容器。假设水平放置的圆槽内充满液体(即液体表面与圆槽周向断口的内沿持平),声波测井仪器与圆槽中心轴一致,且仪器-圆槽模型在轴向为无限长(即忽略圆槽轴向端面的影响)。当圆槽开口角度β较小时,声波仪器完全浸没于液体内(图1(a)),而当圆槽开口角度足够大时,仪器将部分露出液表(图1(b))。
为了研究这种非轴对称结构中的声场和声波响应,我们将采用圆柱坐标系下的应力-速度三维有限差分法对波动方程进行数值计算。在计算中,对圆槽外边界、圆槽断口和液体表面均按应力自由边界进行处理。值得注意的是,由于水平的液体自由表面与圆柱坐标轴方向不一致,所以在模拟液表附近的声场时将参照阶梯状不规则自由边界的应力和速度求取方式[7]。因在仪器发射和接收换能器之间有隔声体存在,可假设弹性波不能直接沿仪器表面传播,模拟时在仪器-流体边界处采用径向位移的刚性边界进行处理。在模型轴向人工截断边界处采用完全匹配层吸收向外辐射的弹性波[8],有关三维交错网格配置和具有二阶精度的差分表达式可参照文献[9-10]。声波测井发射和接收探头均紧贴仪器表面分布的环形分布声压换能器,在环形声源区内各网格的有限差分离散表达式见文献[11]。在计算声波响应时,第n个接收器在t时刻的响应由环向各网格声压的平均值决定
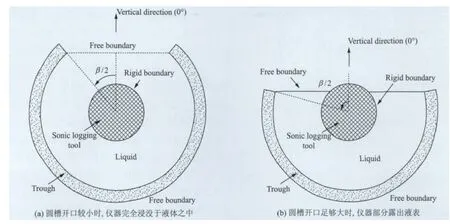
图1 充液圆槽与声波测井仪器横截面示意图Fig.1 Cross sections of the fluid loaded trough and the sonic logging tool

式中(i,j,k)均表示空间网格序号,其中 jmax为环向网格总数,i0表示单极换能器位置的网格径向序号,kn为第n个接收器位置的网格轴向序号。由于在三维有限差分计算中应用了阶梯网格模拟液表自由边界附近的波场,在二阶精度条件下必须采用更精细的网格尺寸以减弱阶梯网格边界导致的人为虚假散射[12]
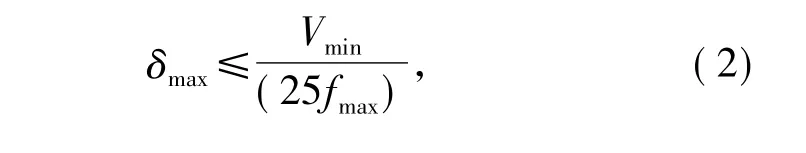
其中δmax表示在计算区域内最大的网格尺寸,Vmin表示模型最小弹性波速,fmax为声源频率的最大值。
3 数值模拟结果
在本节中我们将用三维有限差分算法模拟充液圆槽中的声波场,其中圆槽的材质分别采用代表快速介质的钢铁和黄铜、以及代表慢速介质的有机玻璃。另外我们还对圆槽内载不同液体(甘油、亚麻油、水、柴油和甲醇)情况下的声场特征进行比较,模型物理参数如表1所示。在数值模拟中,设仪器半径为45 mm,并分别记圆槽内半径及壁厚为R和d.以下我们将就单极测井仪器在具有不同物理参数和几何尺寸的模型中的声波响应模拟结果展开讨论。

表1 模型物理参数Table 1 Physic parameters of themodels
图2给出了尺寸(半径、壁厚)相同的封闭圆管及开口圆槽(θ=150°)中声全波形比较,其中声源中心频率为6 kHz,脉冲宽度为0.5 ms,接收器源距为3 m,圆管/圆槽材质分别选取钢、黄铜和有机玻璃,内半径R=120 mm,壁厚 d=21 mm,圆角开口角度β=150°,内载液体为水。波形对比表明,圆管和圆槽中的声波响应具有显著差异,其中圆槽中首波幅度明显低于相同尺寸圆管中的首波。由于在单极子仪器声速刻度中声信号首波是主要的拾取和考察对象,在以下的对比中我们将集中讨论单极子首波的幅度及慢度随着圆槽模型参数的变化情况。

图2 不同材质圆槽和圆管中单极子全波比较Fig.2 Monopole sonic fullwaves related to different modelmaterials
图3(a)给出充水圆槽中归一化首波幅度随着圆槽开口角度的变化情况。图中当0°开口的封闭圆管变为15°开口的圆槽时,首波幅度骤然减小;而后随着圆槽开口的增大,首波幅度进一步以近似线性关系而减小。对比不同的圆槽材质,在相同的开口尺寸条件下,有机玻璃槽中的首波幅度最大,其次是黄铜和钢质圆槽中的首波,即首波幅度随着圆槽介质弹性波速的增大而减小。利用针对声波时域信号的时间-慢度相似相关处理法[13],我们可以提取得全波中首至信号的相慢度值。图3(b)显示,在固定内半径和壁厚前提下,圆管和圆槽中的首波慢度是完全相等的,并未依圆槽开口角度发生任何变化;当R=120 mm、d=21 mm,在载满水的钢、黄铜和有机玻璃圆管/圆槽中由阵列接收器获得的单极测井首波慢度依次为 0.187 ms/m、0.263 ms/m和0.429 ms/m。
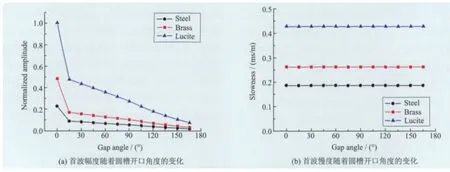
图3 首波幅度和相慢度随着圆槽开口角度的变化情况(其中圆槽尺寸R=120 mm,d=21 mm,假设管内液体为水)Fig.3 The amplitudes and phase slownesses change over trough gap angle of the first arrival wave,where the radius and thickness of the trough are R=120 mm and d=21 mm,respectively.The fluid filled in the trough is water.
我们进一步考察圆槽半径以及壁厚对单极声场首波响应的影响。以150°开口圆槽为例,当圆槽内半径由99 mm变化至225 mm时,不论圆槽材质为钢、黄铜或有机玻璃,首波幅度都呈单调增加的趋势;而在此过程中,首波慢度保持恒定不变,如图4(a)和4(b)所示。如果固定圆槽开口大小及半径而变化其壁厚,首波慢度的变化趋势则与圆槽介质的弹性波速相关:当圆槽由弹性波速远大于水中声速的钢或黄铜制成时,单极声场首波的幅度随着圆槽壁厚的增大而略有减小;而当圆槽介质是弹性波速与槽内液体声速相近的有机玻璃时,首波幅度则随着壁厚增大而增大,但波幅的变化趋势在壁厚d≥27 mm时变缓,相关结果见图5(a)。而对任何介质的圆槽,在这过程中首波的相慢度依然是保持不变的(图5(b))。
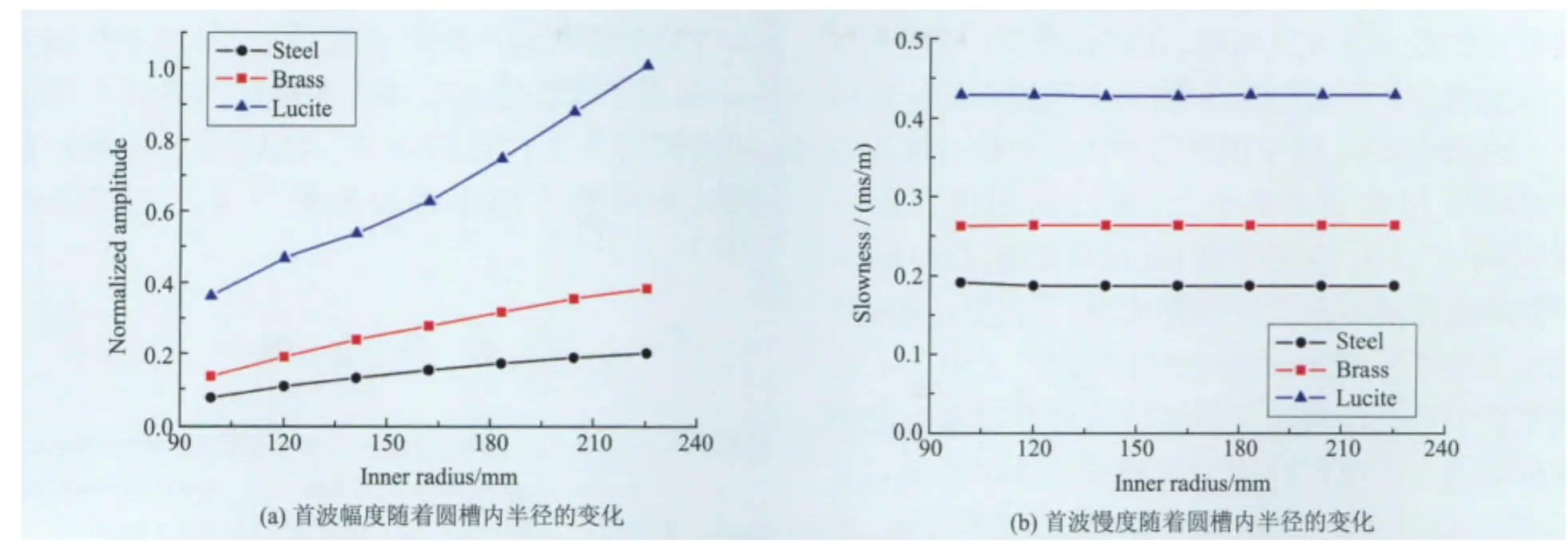
图4 首波幅度和相慢度随着圆槽内半径的变化情况(其中圆槽尺寸β=150°,d=21 mm,假设管内液体为水)Fig.4 The amplitudes and phase slownesses change over trough inner radius of the first arrival wave,where the gap angle and thickness of the trough areβ=150°mm and d=21 mm,respectively.The fluid filled in the trough is water.

图5 首波幅度和相慢度随着圆槽内半径的变化情况(其中圆槽尺寸β=150°,R=120 mm,假设管内液体为水)Fig.5 The amplitudes and phase slownesses change over trough thickness of the first arrival wave,where the gap angle and radius of the trough areβ=150°mm and R=120mm,respectively.The fluid filled in the trough iswater.
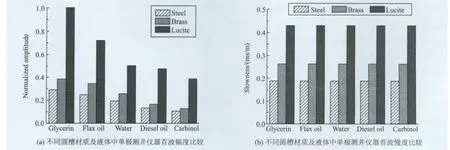
图6 不同液体载荷作用下的首波幅度和相慢度(其中圆槽开口均为30°,内半径均为225 mm,材质为钢和黄铜的圆槽壁厚为15 mm而有机玻璃圆槽厚度为30 mm)Fig.6 The amplitudes and phase slownesses of the first arrivalwave with different loaded liquids,where the gap angles and inner radii areβ=30°and R=225 mm,respectively.The thicknesses are d=15 mm for the steel and brass trough,and d=30 mm for the Lucite trough.
根据上述模拟和分析结果,在仪器测试中为了获得幅度更大的首波响应,在设计模型时,应开口尽可能小且半径较大的圆槽;对于快速介质应选用较小的圆槽壁厚,而采用慢速介质作圆槽时可取适当厚的圆槽模型。基于此,我们选用内半径为225 mm,开口为30°的圆槽(此开口角度保证45 mm半径的仪器可顺利放置于圆槽中),并假定钢和黄铜材质壁厚为15 mm而有机玻璃壁厚为30 mm,在此模型中进一步对比分析槽内液体性质对首波特征的影响。在数值模拟中我们分别采用五种具有不同声速的液体:甘油、亚麻油、水、柴油和甲醇,这五种液体的声速依次减小,参数见表1。计算结果及对比分析表明,单极声场首波幅度对圆槽内液体声速较为敏感,随着液体声速减小而减弱。而对于不同的液体,圆槽中的首波慢度依然是保持恒定的,如图6(a)和 6(b)。李希强等[14]通过频散分析指出,在充液封闭圆管中由于频散曲线“平台”特征[15]的存在,圆管中具有最大群速度的首至波相速度与声源频率无关;根据导波波长与介质尺寸的等比缩放原理,圆管中的首波相速度也不受管材半径及壁厚影响[16]。本文研究结果将此结论进一步推广至充液圆槽中的导波,证实了不论是圆槽还是圆管,单极子声场首波的理论相速度都不受圆槽的几何尺寸、声波的频率以及内载液体特征所影响,完全由仅圆槽介质的物理参数所决定。
4 结论
在本文中,利用三维有限差分算法我们模拟了充满液体的圆槽中单极声波仪器激发的声场,并着重分析了首波信号随圆槽特征的变化情况,研究结论可为单极声波测井仪器的速度刻度和测试模型井的设计提供以下指导意见:
(1)速度刻度。模拟结果表明,不论在圆管还是圆槽中,单极子激发的首波相速度总是相等的,且速度值不受圆槽开口大小、半径、壁厚以及液体性质所影响,仅由圆槽材质的物理特征(密度、纵波和横波速度)决定。因此在进行仪器声速刻度时,可以用水平放置的载液圆槽代替竖直放置的充液圆管,实现更简便、易于实施的仪器标定方式。
(2)换能器测试。为了在正常的单极测井仪器测试中观测到更强的首波信号,相对于快速介质,采用弹性波速与液体声速接近的慢速介质制成的圆槽具有较好的效果。同时建议在设计圆槽时选用较大的半径和壁厚以及尽可能小的开口。
[1]GAZISD C.Three-dimensional investigation of the propagation of waves in hollowcircular cylinders:I.Analytical foundation[J].J.Acoust.Soc.Am.,1959,31(5):568-573.
[2]GAZISD C.Three-dimensional investigation of the propagation ofwaves in hollowcircular cylinders:II.Numerical results[J].J.Acoust.Soc.Am.,1959,31(5):573-578.
[3]SINHA B K,PLONA T J,KOSTEK S,et al.Axisymmetric wave propagation in fluid-loaded cylindrical shells:I:Theory[J].J.Acoust.Soc.Am.,1992,92(2):1132-1143.
[4]PLONA T J,SINHA B K,KOSTEK S,et al.Axisymmetric wave propagation in fluid-loaded cylindrical shells:II:Theory versus experiment[J]. J. Acoust. Soc. Am.,1992,92(2):1144-1155.
[5]WANG X,DODDS K.Effects of the outermost boundary on acoustic waves in an artificial cased borehole [J].Explor.Geophys.,2002,33(4):146-152.
[6]ARISTEGUIC,LOWE MJ S,CAWLEY P.Guided waves in fluid-filled pipes surrounded by different fluids [J].Ultrasonics,2001,39:367-375.
[7]WANG X,ZHANGH.Modeling of elastic wave propagation on a curved free surface using an improved finite-difference algorithm[J].Sci.China Ser.G.,2004,47(5):633-648.
[8]WANG T,TANG X.Finite-difference modeling of elastic wave propagation:A nonsplitting perfectly matched layer approach[J].Geophysics,2003,68(5):1749-1755.
[9]HE X,HU H,GUAN W.Fast and slowflexural waves in a deviated borehole in homogeneous and layered anisotropic formations[J].Geophys.J.Int.,2010,181(1):417-426.
[10]HE X,CHEN H,WANG X.3D finite difference simulations of acoustic logs in tilted layered porous formations[J].J.Comput.Acoust.,2012;20(2):1240009.
[11]HE X,HU H,WANG X.Finite difference modelling of dipole acoustic logs in a poroelastic formation with anisotropic permeability[J].Geophys.J.Int.,2013,192(1):359-374.
[12]OHMINATO T,CHOUET B A. A free-surface boundary condition for including 3D topography in the finite-difference method [J]. Bull. Seism. Soc. Am.,1997,87(2):494-515.
[13]KIMBALL C V,MARZETTA T L.Semblance processing of borehole acoustic array data [J].Geophysics,1986,49(3):274-281.
[14]LIX,CHEN H,HE X,et al.Analyses on dispersions and excitations of symmetric guided waves in a fluid-filled cylindrical shell[C].IEEE Symposium on Piezoelectricity,Acoustic Waves and Device Applications,2012,277-280.
[15]王晶,陈德华,张海澜,等.外表面应力自由的充液有限壁厚井孔中的声场及其频散曲线的“平台”特征[J].声学学报,2012,37(3):232-236.WANG Jing,CHEN Dehua,ZHANG Hailan,et al.Wavefield in a fluid-filled cylindrical shellwith outside traction-free boundary conditions and its“plateau”characteristics in dispersion curves[J],Acta Acustica,2012,37(3):232-236.
[16]他得安,刘镇清.超声导波频散特性与管材内径-壁厚比的关系[J].复旦学报(自然科学版),2003,42(1):7-13.TA De'an,LIU Zhenqing. Relationship Between Dispersive Characteristics of Ultrasonic Guided Waves and Inner-radiusthickness Ratio of Pipes [J].J.Fudan U.(Natur.Sci.),2003,42(1):7-13.

