基于单端信息量的特高压串补线路距离保护方案
郑 涛,高 超,赵 萍
(1.华北电力大学 新能源电力系统国家重点实验室,北京102206;2.台州电业局,浙江 台州317000)
0 引 言
线路安装串联补偿装置可以很好地提高系统的经济性和可靠性,在我国高压远距离输电线路中得到了广泛地应用[1~6]。随着特高压电网的建设,智能电网工程的推进,串补因其改善电力系统稳定性,提高电能质量及线路传输功率,减少线路损耗的优势,在未来的电网建设中,应用前景将更加广阔。然而,串补电容破坏了输电线路参数的均匀性,可能造成电压电流反向,并在故障信息中引入大量低频分量及衰减的非周期分量,给传统继电保护尤其是距离保护产生不利的影响[7~13]。MOV 导通时,其非线性将进一步加大传统距离保护可靠动作的难度。
为解决安装串补之后给传统距离保护带来的问题,当前主要有两种方案[1,2]:一是改变线路整定值,即利用线路阻抗和串补容抗之和进行整定,利用ZJ=ZL- |ZC|,但随着补偿度的增高,保护灵敏性将逐渐降低,甚至降为零;二是利用电平检测方案,即假设串补电容两端的电压一直保持在其过电压保护水平上,并由此构建保护判据,此方案在故障发生在串补装置前以及故障发生在串补装置后但串补电容被旁路的情况下,可能会出现保护拒动的问题。
当前,对于串补线路的故障定位方法有了较大的发展。文献[1]利用故障后到MOV 导通前的暂态信息进行模型识别,实现故障点的快速定位。但这种方法是在单相故障的基础上提出的,在适用范围上具有一定的局限性。文献[3,4]利用串补装置的等值阻抗来估计串补两端的电压,用于故障定位。但此方案仅利用工频信息,特高压串补系统含有大量的低频分量和高频分量,仅使用工频量进行故障定位有失准确性。文献[5]利用串补安装在线路末端的模型,假设串补电容前的电压为补偿电压,通过分析故障发生在串补装置前后时补偿电压的幅值及相位的不同来确定故障点相对串补装置的位置,此方案未考虑过渡电阻地影响,对过渡电阻的适应性不足。
本文提出了一种基于单端信息量的特高压串补线路故障测距方案,根据故障状态网络和故障附加网络,得到了以故障距离及过渡阻抗为未知量的时域方程组。该算法不必事先确定故障点相对串补的位置,对过渡电阻有较强的适用性。同时,利用故障后到MOV 导通前的暂态数据快速识别故障位置,能够避开了MOV 的非线性影响,具有较高的可靠性。PSCAD 仿真证明,该方案在各种故障状态下均可实现快速准确地故障定位,具有较高的可靠性。
1 基于单端信息量的距离保护基本原理
首先,采用单相系统模型,推导保护算法的基本原理。双端电源的单相故障线路如图1 所示。
图中iM,iN为故障时M,N 两侧的电流瞬时值;uM,uN为故障时M,N 两侧的电压瞬时值;uf,if为故障点的电压电流瞬时值;Rf为故障时的过渡电阻值;eM,eN为双端系统的等值电源;z 代表单位长度的线路阻抗值,其可表示为r + jx 的形式;ld1,ld2分别为M 侧及N 侧到故障点的距离;XC串补电容的容抗值。
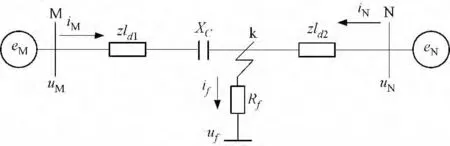
图1 故障状态的等值电路图Fig.1 Equivalent circuit of fault station
由图1 可以列写故障状态下系统方程式为
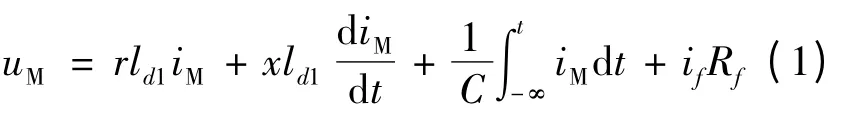
对其两边取微分得:

公式(2)中:r,x 为线路参数;C 为串补电容的容抗值,均为已知量;uM,iM为采样数据,其一阶及二阶微分值可以利用差分代替微分的方式求得,即

式(3)中:TS为采样间隔;n 为采样时刻。此时,系统方程中未知参量为ld1,Rf,if。如使用叠加定理,将故障后的网络拆为正常工作状态网络及故障附加网络,利用故障附加网络电流关系可求得故障电流if。网络结构如图2 所示,图中uMq,iMq为系统正常工作时M 处测得的电压值及负荷电流值;uMh,iMh为系统故障后M 处测得的电压及电流值;iNh故障后N 处测得的电流值;故障附加网络中故障分类满足ΔuM= uMh- uMq,ΔiM= iMh- iMq。
根据图2(b)中的线路关系可得:

特高压线路中线路电阻远小于线路电感,故存在l′ = XC/z ≈XC/x = kCl。其中KC为线路的串补度,l 为线路的总长度。从而方程(4)可化简为

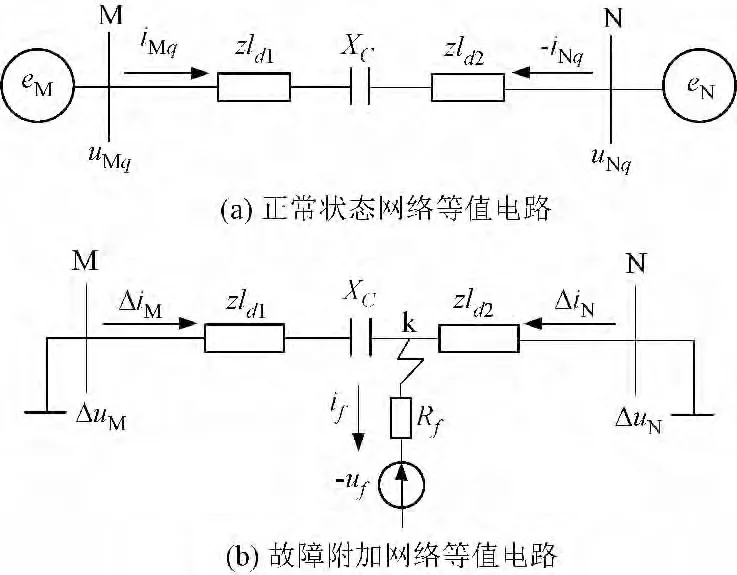
图2 故障状态下叠加原理分解图Fig.2 Superposition principle diagram of fault condition network
推导测距方程式为

式中:

线性方程组(6)中有3 个系数,理论上取3 个不连续采样点的电压、电流数据建立3 个方程的线性方程组:
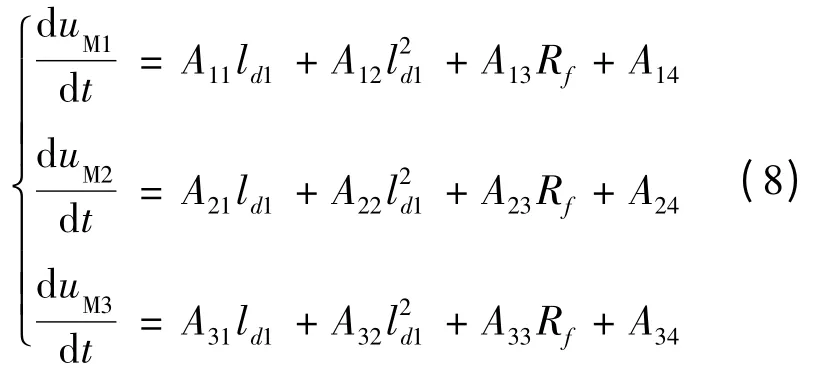
利用此线性方程组可以准确测得故障距离ld1,及过渡电阻Rf的大小:
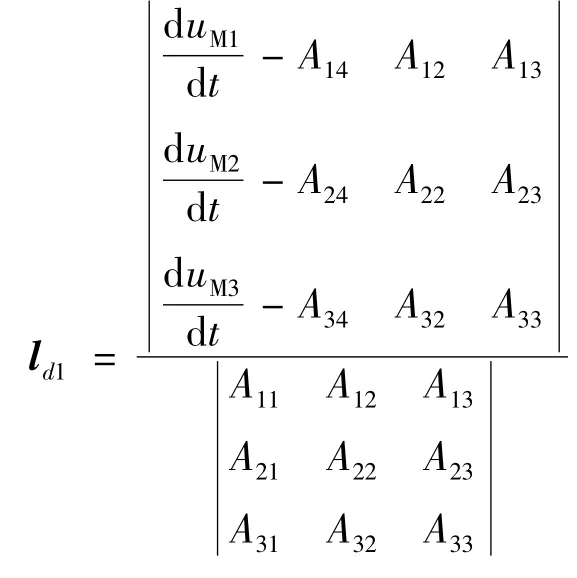

故障距离ld1的计算公式中,串补电容值体现Aij(i=1,2,3,4;j =1,3,4)中,经矩阵计算,发现串补电容值对故障距离ld1的测距结果影响不明显,该算法可同时适用于串补前和串补后故障。
2 三相串补系统保护算法
2.1 三相线路的序网变换矩阵
三相输电线路存在复杂的耦合关系,在分析三相线路时应先进行解耦分析。由故障分析理论[14]可知,通过变换矩阵方式可将三相系统解耦分解为3 个序网系统。本文算法基于时域参数,利用对称分量法将其分解为3 个序网(正序,负序,零序),其变换矩阵为

式中:a = ej120°,F 为电流或者电压值。
2.2 单相接地故障
当输电线路发生单相接地故障(以a 相故障为例)时,给出故障系统等效电流图如图3 所示:

图3 单相接地短路系统模型Fig.3 Single-phase-to-earth fault system model
经序网变换后,可以得到A 相接地时M 侧的电压电流方程式为
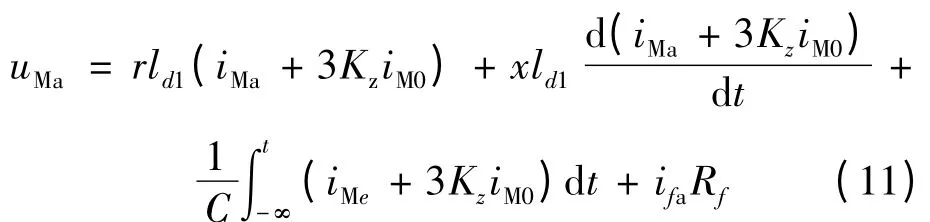
式中:Kz= (z0- z1)/z1为阻抗的零序补偿系数;z0,z1为线路的零序和正序的单位长度阻抗值;uMe,iMe,iM0是故障状态下M 侧测得的A 相母线电压电流及零序电流采样值;ifa为双端故障电流之和,满足ifa= iMa+ iNa。由于仅采用单端信息,对侧电流iNa未知,ifa无法直接求取。考虑到单相接地系统存在电流关系ifa= 3if0,通过零序网络可以求得零序故障电流值if0。因此,使用零序网络对故障电流进行求解。

图4 单相接地短路零序系统图Fig.4 Zero system of single-phase-to-earth fault
同样,考虑到特高压情况下线路的电抗甚大于电阻,可忽略线路电阻,此时根据图4 所示的零序网络图可得到方程:

零序测量电流iM0可通过三相电流关系iM0=(iMa+ iMb+ iMc)/3 求取,考虑ifa= 3if0,将公式(8)、(9)联立可得到单相接地情况下的测距方程:
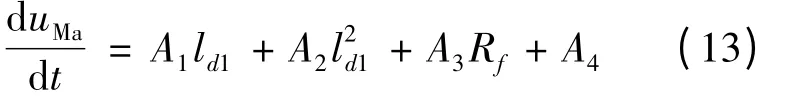
式中:

方程中的未知参数为ld1,l2d1,Rf,其中l2d1 是关于ld1的函数,因此,待求量为ld1与Rf。为准确计算,采用冗余方程,利用3 个不同的采样点进行分析,可得到3 个非线性方程组,从而准确的得到故障距离。
2.3 相间短路故障
对于相间短路情况,其过渡电阻较小,多为电弧电阻,一般可以忽略。假设BC 两相短路时,有:
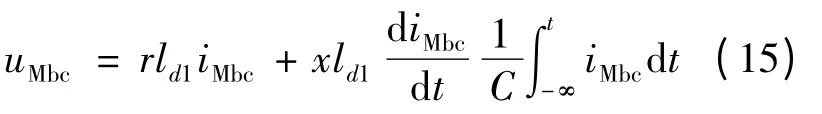
式中:uMbc,iMbc为BC 两相的电压差和电流差,对其两端微分整理后可得到其测距方程:

利用测距方程可得到两相短路时的故障距离。
2.4 三相短路故障
系统的三相短路故障是对称性故障,在理论上其可以完全等价为单相系统模型,故而第1 节中给出的单相系统测距方案可以直接应用到三相系统的三相短路情况,并得到准确的故障位置。
3 仿真验证
本文所提到的保护方案利用单端信息量进行故障测距,从而实现距离保护。在保护算法中,使用了差分代替微分的方式,为提高保护算法的可靠性,需考虑提高采样频率。同时,考虑到MOV导通后的非线性过程可能会对测距带来误差,而根据文献[1]可知,在故障初期的几个ms 内,MOV处于未导通状态,串补装置显现为纯电容状态。综合考虑算法误差和工程实际,选取采样频率为10 kHz 具有较好的测距效果,并可以适用于工程应用。采用PSCAD/EMTDC 搭建了特高压串补线路模型进行故障仿真,并利用MATLAB 编程实现了文中所述的基于单端量的距离保护方案。1 000 kV 特高压串补系统如图5 所示。

图5 特高压串补线路示意图Fig.5 UHV series compensated transmission line
系统参数:z1=0.009 39 +j 0.270 20 Ω/km;z0= 0.175 70 + j 0.780 40 Ω/km;c1= 0.013 79 μF/km;Co = 0.008 66 μF/km。系统串补度为50 %,取电容值为58.9 μF。串补电容安装在线路中间(200 km 处)。选取2 个故障点k1(距离保护安装处100 km),k2(距离保护安装处300 km)进行仿真验证。仿真结果如图6 所示。

图6 故障仿真曲线Fig.6 Simulating faults curve
图6 中的曲线在故障后有个暂态趋稳的过程,根据图7 可分析其产生原因。

图7 100 km 处故障后的母线M 侧电流Fig.7 Current after the fault of bus M side when fault case in 100 km
由图7 可以看出,故障初期,故障电流含有大量的非周期分量,在一段时间后趋于稳定。因此,在故障初期,利用差分代替微分将带来较大的误差,仿真结果有一定的波动。本文选取采样频率较高,系统很快就趋于稳定。图6 中故障点分别设置在串补装置前和串补装置后,由仿真结果可以看出,在串补装置前后故障,本算法均有较好的测距精度。同时,本算法对MOV 的不同导通状态也有较好的适应性,当MOV 处于旁路阶段时,可近似认为串补电容被短接,此时故障类型近似认为串补前故障。当MOV 处于导通状态时,此时FSC 装置处于非线性状态,串补装置等效阻抗随电流变化规律如图8 所示[2]。

图8 MOV 导通时串补装置的等效阻抗Fig.8 Equivalent impendance of MOV-Protected series compensator after fault
图8 中阻抗及电流均以标幺值形式表示,阻抗基准值为串补电容XC,故障电流幅值Ip.u.满足Ip.u.=I/Ipl,其中I 为流过串补装置的电流值,Ipl为MOV 的最小导通电流。由图8 可以看出,当Ip.u.不大时,串补装置的等值阻抗Z′C约为(0.4 ~0.9)XC。此时,根据式(9)可知,其对测距结果影响不大,本文算法受MOV 导通影响不大。
为测试不同故障位置及经不同过渡电阻时保护算法的可靠性,选用不同故障位置进行测试,其测试结果如表1 所示。

表1 不同故障位置的测距结果Tab.1 Simulation results at different points
针对不同过渡电阻下的测距情况进行仿真,将其故障测距结果如表2 所示。

表2 不同过渡电阻下的测距结果Tab.2 Simulation results at different fault resistance
设测距相对误差的计算公式为

由表1 及表2 的仿真结果可以看出,本文所述的基于单端信息的距离保护方案可以实现准确测距,并具有较高的测距精度。即使在线路接有高过渡电阻的情况下,其测距误差也在5 %以内。同时,由仿真结果可以看出本算法无需确定故障点相对串补的位置,即在串补前及串补后故障均可以准确测距。
4 结 论
本文提出了一种利用单端信息量进行保护测距的距离保护算法。该算法适用于串补线路,可以实现串补线路的准确故障定位。其有以下几点优势:(1)根据串补线路故障时的暂态信息进行故障测距,直接判断出故障位置,可以避免传统保护算法中的暂态超越问题。(2)该算法对于串补系统适应性较好,无需事先判断故障点相对串补的位置,直接决定串补线路保护是否动作。(3)通过高采样频率减少了差分代替微分的误差,可以在MOV 进入非线性之前确定故障位置,避开了MOV 的非线性影响。(4)算法对于过渡电阻有较好的耐受能力。通过大量仿真表明,该保护方案可以很好判断故障位置,保证了距离保护的可靠性。
[1]索南加乐,陈福锋等.串补线路故障点位置的模型识别方法[J].中国电机工程学报,2005,25(1):66 -72.
[2]焦在滨,张梦瑶等.基于频域模型识别的串补线路保护方案[J].中国电机工程学报,2013,33 (4):186 -193.
[3]韩彦华,施围.串补输电线路的精确定位算法[J].中国电机工程学报,2001.21 (3):1 -5.
[4]J.Sadeh,A.M.Ranjbar,et al.Accurate fault location algorithm for.series compensated transmission lines [J].IEEE 2000:2527 -2532.
[5]陈福锋,钱国明,薛明军.适用于串联电容补偿线路的距离保护新原理[J].电力系统自动化,2010,34 (12):61 -66.
[6]Qisheng,L.,et al.Studies on series compensation of UHV transmission line.in Power System Technology(POWERCON),2010 International Conference on.2010.
[7]朱声石.高压电网继电保护原理与技术[M].3 版.北京:中国电力出版社,2005.
[8]Coursol M,Chinh T N,Rene L,et al.Modeling MOVprotected series capacitors for short-circuit studies [J].IEEE Transactions on Power Delivery,1993.8 (1):448 -453.
[9]Rai,D.,et al..Enhancement of Power System Dynamics Using a Phase Imbalanced Series Compensation Scheme.Power Systems.IEEE Transactions on.2010.25 (2):966 -974.
[10]刘淑磊,陈福锋,何奔腾.基于补偿点阻抗的阻抗角特性的串补线路距离保护原理[J].电力系统自动化,2010.34 (21):70 -74.
[11]de Oliveira,A.L.P.and P.M.Da Silveira.Evaluation of Distance Protection Performance applied on Series Compensated Transmission Lines using Real Time Digital Simulation.in Transmission & Distribution Conference and Exposition: Latin America, 2006.TDC′06.IEEE/PES.2006.
[12]索南加乐,谈树峰,何世恩等.基于模型识别的串补线路方向元件[J].电力系统自动化,2009,33(14):66 -70.
[13]王兴国,黄少锋.超高压长距离输电线路故障暂态分量的研究[J].华北电力大学学报,2009,36(2):6 -12.
[14]张保会,尹项根.电力系统继电保护[M].2 版.北京:中国电力出版社,2005.

