基于ANSYS的弧面三角闸门自振特性研究

胡剑杰 胡友安 王 煦

（1.河海大学 机电工程学院，江苏 常州 213022；2.江苏省水利勘察设计研究院有限公司，江苏 扬州 225127）

水工钢闸门在运行过程中，水流的脉动作用会引起闸门结构会产生不同程度的振动.多数情况下，闸门的振动幅度较小，不会影响闸门的安全运行，但是在某些特殊的条件下［1］，会出现很强烈的振动，引起闸门动力失稳或发生共振，最终导致闸门结构破坏.一般情况下，闸门结构自身的自振特性是引起闸门振动破坏的内在原因［2－3］.闸门振动受其结构布置、约束条件以及周围水体的影响，无水约束状态下自振特性容易求得，但水体对闸门结构自振特性的影响程度难以确定［4］.在水体影响下，研究闸门自振特性的影响因素，并分析计算出闸门的自振频率和振型，可为闸门结构优化和动力学特性的设计提高参考依据.

本文结合某船闸弧面三角闸门实例，基于ANSYS建立闸门的数值分析模型，考虑流固耦合效应，研究水体作用下弧面三角闸门自振特性的影响因素，分析闸门干模态与湿模态下的自振频率和相应振型，为相关理论依据作进一步补充.

1 闸门的模态分析原理

1.1 干模态法

无水约束条件下，没有水体对闸门的影响，闸门结构动力学平衡方程为

式中，M为闸门的质量矩阵、C为阻尼矩阵、K为刚度矩阵；u为结构总的结点自由度向量；FG为作用在闸门结构上的其他载荷向量［5］.

为求解空气中闸门结构的固有频率，可令阻尼矩阵C、载荷向量FG为零，即可得到闸门结构的自由振动方程：

1.2 湿模态法

闸门在水体中工作时，闸门自身振动会引起水体压力的波动变化，水体压力的变化反过来又会引起闸门的振动.因而，在考虑流固耦合效应时，需要对无阻尼弹性体的自由振动方程作相应的修正［6］.

有水体作用时，闸门结构的自由振动方程可以表示为

式中，P为流固耦合面上有关节点的动水压力向量，式（3）为流固耦合振动方程.

对于无黏性不可压缩的微幅流体运动，动水压力向量P与水流扰动速度势Φ（x，y，z，t）满足如下关系

式中，ρ为边界条件参数，在已知的边界条件下，以及流固耦合作用面表面法向加速度与水质点的法向加速度相等，且远处水体的扰动速度和扰动压强均趋于零，故可得

式中，Mp为附加质量矩阵.

将式（5）代入式（3）整理可得

式（6）为水体作用下闸门结构自由振动的耦合控制方程［5］.

1.3 建立闸门数值模型

本文有限元模型以某船闸弧面三角闸门为背景，闸门面板半径8.1m，门高8.52m.在水压力作用下，闸门的面板、主梁、隔板都会发生弯曲、扭转、剪切等组合变形.对于板梁组合结构的弧面三角闸门，建立有限元模型时，各梁和空间杆件均采用beam188单元模拟，面板结构采用shell63单元模拟［7］.图1为闸门结构的几何模型，在ANSYS中对整个闸门进行网格划分，生成有限元模型包含7 209个板单元，2 602个梁单元，节点总数为9 509.

闸门约束条件：顶枢水平面内的位移约束x，y；底枢水平面内和竖直方向的位移约束x，y，z；启闭杆处的位移约束x，y；闸门中缝轴线接触面处的对称约束；闸门面板底部与底槛接触处的位移约束z.

图1 弧面三角闸门结构几何模型

考虑流固耦合效应时，水体采用Fliud30单元模拟，建立ANSYS有限元模型如图2所示.

图2 水体作用下弧面三角闸门有限元模型

2 闸门自振特性计算与分析

本文对三角闸门处于关闭蓄水工况下的自振特性进行研究，分别计算在约束条件下无水和有水状态闸门结构的自振频率.其中，重点分析流固耦合效应对闸门自振频率的影响.第一，分析计算闸门面前水体高度对闸门自振频率的影响；第二，比较闸门面前水体宽度对闸门自振频率的影响；第三，对比有水和无水状态下闸门整体振型的变化.

2.1 流固耦合对闸门自振频率的影响

研究三角闸门自振特性时，由于闸门的低阶振型表现为闸门结构的整体振动，且低阶自振频率较低，与水流主要脉动频率区接近，容易被激发；而高阶振型表现为闸门的局部构件振动，对闸门整体结构的安全不会造成很大影响［8］.因此，本文仅对弧面三角闸门的前二十阶自振特性进行分析.

表1和图3是闸门结构在无水和有水情况下的振动频率比较.由表1的数据分析可知，水体对闸门的低阶和高阶振动频率影响较大.施加流体后，闸门的振动频率均小于无水状态下的振动频率，其中，一阶、二阶频率降低百分比为13.92%、22.04%，低阶自振频率受水体作用十分明显.十三阶以后自振频率受水体影响作用差别不大，频率平均降低百分比为2.42%，水体对闸门高阶自振频率影响也较为明显.

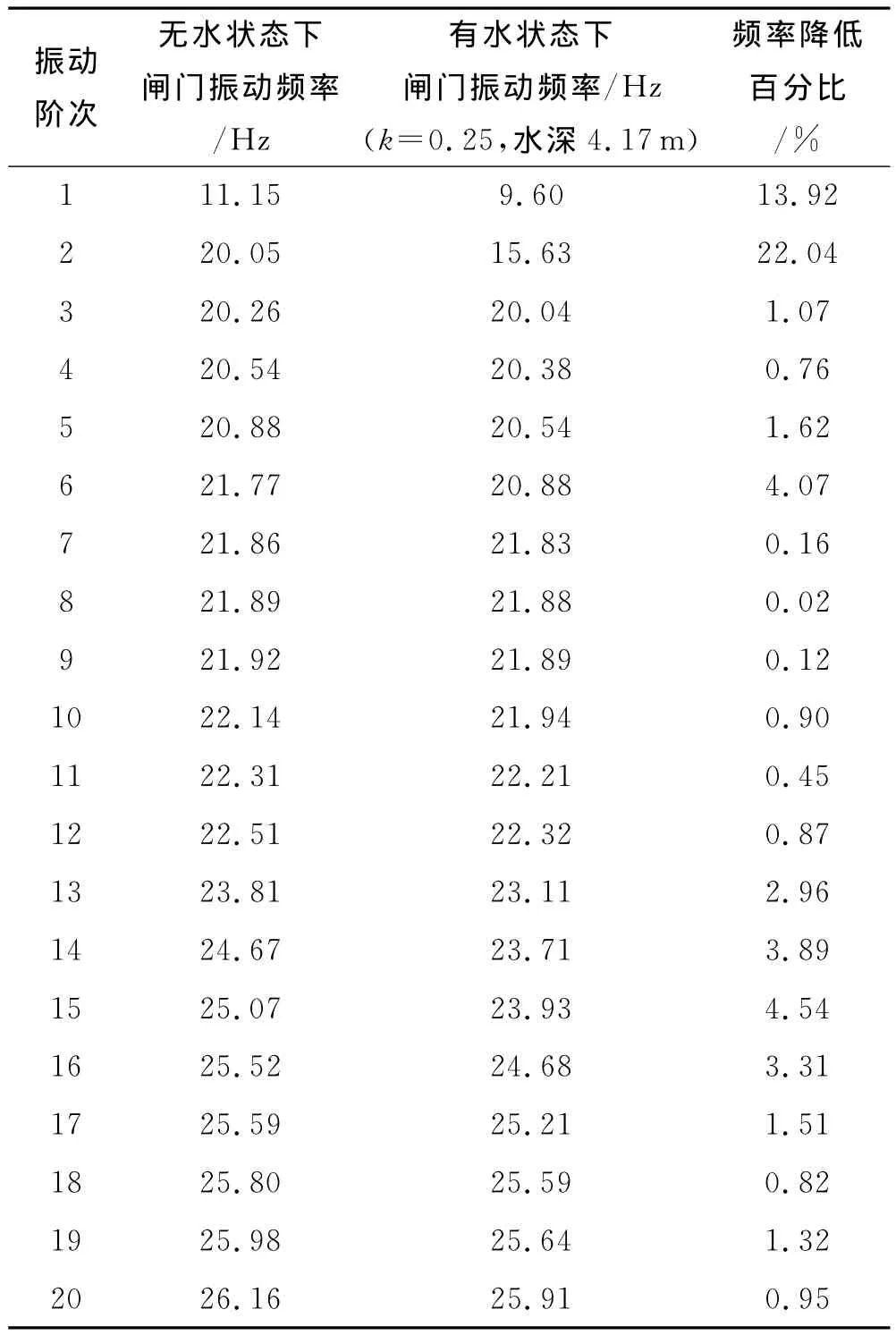
表1 流固耦合对弧面三角闸门自振频率的影响

图3 流固耦合效应对闸门自振频率的影响

另外，由图3可知，闸门振动频率也随着闸门面前水体高度变化而变化，水深8.02m相对于4.17m自振频率明显降低.即有规律：水体高度越大，闸门振动频率越低.其主要原因是随门前水体高度增大，附加水体质量也随之增大，流固耦合效应越明显.

2.2 水体宽度对闸门自振频率的影响

考虑到闸门前水体宽度对闸门的自振特性也有影响，另需改变门前水体宽度，分析闸门自振频率的变化程度.取水体宽度为闸门高度的0.25、0.5、1.0倍，计算出3种水体宽度下闸门的振动频率值，可分析出水体宽度对闸门自振特性的影响.表2是闸门结构在不同水体宽度下的振动频率.

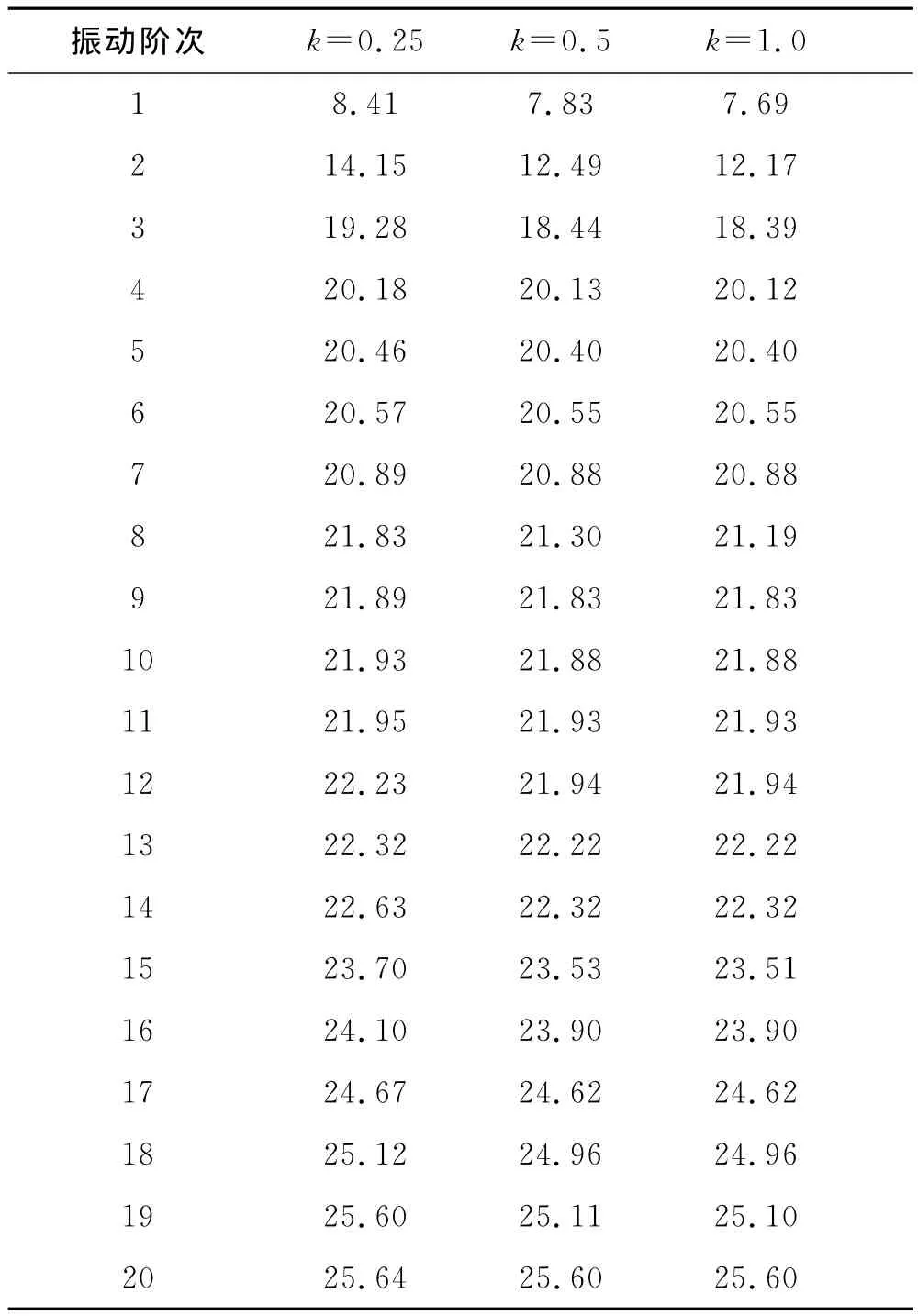
表2 弧面三角闸门结构在不同水体宽度下的振动频率

分析水体宽度对闸门自振特性的影响可以发现，闸门振动频率随着水体宽度增大而逐渐减小，水体宽度对闸门低阶振型的自振频率影响作用较为明显.闸门结构基频随水体宽度增加大小分别为8.41Hz、7.83Hz、7.69Hz，降低百分比为6.90%、1.79%，二阶自振频率降低百分比为11.73%、2.56%，均呈减小趋势.

水体宽度为闸门高度的0.25、0.5、1.0倍时，前20阶自振频率降低幅度随水体宽度增加而减小.当水体宽度为闸门高度1.0倍时，四阶以后自振频率趋于不变.依此规律，门前水体宽度达到1～2倍闸门高度，各阶频率值几乎不再变化，闸门结构受水体宽度的影响程度可以不计.综上可知，流固耦合效应对闸门自振特性的影响程度较为明显，闸门面前水体宽度和高度是影响闸门自振频率大小的重要因素.

2.3 闸门振型的分析

通过对闸门有限元计算网格进行模态分析，查看闸门结构的各阶振型.无水状态下，第一阶为门叶整体横向的摆动（绕端柱轴），第二阶为门叶整体沿弧面径向的振动，第三、四阶为闸门整体沿弧面径向弯曲扭转振动，四阶以后振型表现闸门空间杆件的局部振动.

在水体作用下，当水深为闸门宽度的0.25倍时，提取闸门相关振型，可分析出水体流场对闸门振动规律的影响.图4～5给出了水深为4.17m的一、二阶振型图.

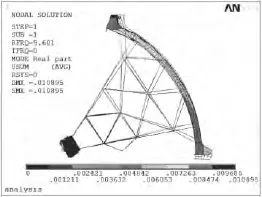
图4 水深4.17m闸门整体一阶振型

图5 水深4.17m闸门整体二阶振型

由提取结果可知，有水体影响时，第一、二阶振型分别为门叶整体的横向摆动（绕端柱轴）、门叶整体沿弧面径向振动，振动型式与无水条件下闸门振型类似，变形程度相对较小.二阶以后振型均为空间钢架局部弯曲振动.对无水干模态振型分析，四阶之后振型均表现为空间桁架的局部弯曲振动，而在流固耦合影响下，二阶之后振型多为桁架局部杆件弯曲振动，表明水体流场影响下，闸门整体稳定性较好.

高阶振型不会对闸门整体造成较大影响，而低阶自振频率及振型与闸门整体结构的振动破坏息息相关，设计校核时应予以考虑.

3 结 语

1）闸门结构自振特性与闸门面前水体产生的流场有关，研究闸门自振特性时，流固耦合效应不可忽视.流固耦合作用下，闸门自振频率相对于无水约束条件明显降低，低阶振型也发生了变化，振动型式受水体作用力影响.

2）闸门自振频率受门前水体宽度和高度的影响：闸门面前水体高度越高，其自振频率越低；闸门面前水体宽度越宽，自振频率也越低.其中，闸门低阶自振频率受门前水体高度与宽度影响较大，中高阶自振频率受影响较小.另外，随门前水体宽度逐渐增大，闸门自振频率趋于不变.

3）闸门动力分析时，需比较闸门自身自振频率与水流脉动频率，使闸门设计频率远离水流脉动频率，确保闸门运行安全［9］.本文所作研究得到的结果，为闸门结构和动力学设计提供参考依据，可供同类型闸门振动稳定性研究借鉴.

［1］ 邱徳修，朱召泉，邱 琳.弧形钢闸门流固耦合自振特性分析［J］.广东水利水电，2010（1）：10－12.

［2］ 赵兰浩，李同春，汪 凌.水工闸门流激振动响应的一种计算方法［J］.河海大学学报：自然科学版，2005，33（4）：404－408.

［3］ 兰文改，周 娟，高东辉.平面钢闸门自振特性有限元分析［J］.人民黄河，2009，31（8）：112－113.

［4］ 古 华，严根华.水工闸门流固耦合自振特性数值分析［J］.振动、测试与诊断，2008，28（3）：242－246.

［5］ 许 敏，薛惠芳.基于ANSYS的平面闸门自振特性研究［J］.人民长江，2011，42（Z2）：150－151.

［6］ 严根华，阎诗武.水工弧形闸门的水弹性耦合自振特性研究［J］.水利学报，1990（7）：49－55.

［7］ 胡友安，王 孟.水工钢闸门数值模拟与工程实践［M］.北京：中国水利水电出版社，2010：24－27.

［8］ 王均星，焦修明，陈 炜.龙滩工程底孔弧形闸门的自振特性［J］.武汉大学学报：工学版，2008，41（5）：31－34.

［9］ 刘 晶，高学平.基于ANSYS的拱形闸门自振特性研究［J］.水资源与水工程学报，2011，22（6）：162－164.