高中物理教学中渗透数学思想方法的价值研究*
徐卫兵
(西安交通大学苏州附属中学,江苏 苏州 215021)
数学是物理学的表述形式,是创立和发展物理学理论的主要工具、是解决物理问题的重要工具.这说明数学对物理学有着深远的影响.因此,在高中物理教学中渗透数学思想方法,培养学生应用数学知识解决物理问题的能力就显得非常重要.这对学生们的后续学习和今后从事科学研究,提高他们的创新能力有着重要意义.本文依据数学与物理的现实联系以及素质教育的需要,从数学和物理的关系,从教师和学生的角度,谈谈在高中物理教学中渗透数学思想方法的价值.
1 问题的提出
在目前的高中物理教学中,发现有不少学生数学学得很好,但是在需要运用这些数学知识来解答物理问题时,却不能很好的把所学的数学知识用来分析和解决物理问题.面对这种情况,部分物理教师把原因片面归结于数学教学上.而据我们调查,一些物理教师在教学过程中,由于担心“把物理课上成数学课”,对必要的数学推导和运算往往处理得过于草率,没有能引起学生的重视;在高中阶段遇到的各类习题中,有很多是数、理之间紧密联系的题目,教师又没有能做到示范引领作用,从而使学生在运用物理知识进行分析、解题时,没有注意在解题过程中灵活运用所学到的数学思想方法.正是由于存在着以上两方面对数学、物理之间的联系认识不够,在很大程度上影响了众多学生学习物理的兴趣和成绩.
图1
其实人类的知识本身就是一个有机的整体.在狭隘学科观念背景下,过分地局限于本学科知识的讲授,这样的教学目标缺少系统化和结构化,不仅禁锢教师教学思想的自由驰骋,也不能帮助学生形成有机的完整的人类知识图景,还会肢解完整的精神生产过程,导致智慧能力的片面畸形发展,永远不会培养出视野开阔,才思敏捷的人才.
物理学是研究最普遍的运动形式和基本结构的科学,而数学则是研究现实空间形式和数量关系的科学.虽然他们研究的对象各不相同,但却有着共同的目的,即探索和研究自然界的有关规律,并在实践中加以运用,这就使二者之间产生了必然联系,如图1所示.纵观物理学与数学的发展历程,它们是在相互影响,相互促进中发展起来的.正如诺贝尔奖获得者杨振宁指出:“可以用两片生长在同一根管茎上的叶子,来形象化地说明数学与物理之间的关系.数学与物理是同命相连的,他们的生命线交接在一起”.[1]例如,1862—1864年,麦克斯韦建立了著名的麦克斯韦方程组,以非常简洁、优美的形式包含了库仑定律、欧姆定律、安培定律和法拉第电磁感应定律等,统一解释了各种宏观的电磁过程,并且从这个纯数学形式的方程组出发,麦克斯韦提出并从理论上证明了光也是一种电磁波,预言了电磁波的存在,从而把电、磁、光统一起来,实现了物理学史上一次大的飞跃.
2 在高中物理教学中渗透数学思想方法有利于贯彻物理课程理念
高中物理从课程、教材、考纲3个方面都对高中物理教学中渗透数学思想方法提出了明确的要求.
2.1 贯彻课程理念
《高中物理课程标准》有助于学生体验科学探究过程,了解科学研究方法.提出学生要经历科学家的探究过程,认识科学探究的意义,尝试应用科学探究的方法研究物理问题,验证物理规律.通过物理概念和规律的学习过程,了解物理学的研究方法,认识物理实验、物理模型和数学工具在物理学发展过程中的作用.探究的操作活动包括观察、提问、实验、比较、推理、概括、表达、运用及其他活动.其中很重要的一点就是把观察所得的结果用精确的数学关系表达出来,运用数学语言来描述分析资料.高中物理课程渗透了很多数学思想方法,在教学中不断挖掘课程中的数学思想,让学生意识到自然科学乃至社会科学统一于数学的大思想,并培养学生科学的物理思维,具有很大的现实意义.
2.2 落实教材
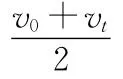
2.3 实施考纲
《物理高考考纲》(又称《物理高考考试说明》)年年都要修订,但其中明确提出的一个能力是不变的,只是更具体,那就是考生应具备的应用数学知识处理物理问题的能力:能够根据具体问题列出物理量之间的数学关系式,根据数学的特点、规律进行推导、求解和合理外推,并根据结果得出物理判断、进行物理解释或得出物理结论;能根据物理问题的实际情况和所给条件,恰当运用几何图形、函数图像等形式和方法进行分析、表达;能够从所给图像通过分析找出其所表达的物理内容,用于分析和解决物理问题.这在各地每年的高考试题中都有体现,如2014年江苏高考物理试卷第5题,一汽车从静止开始做匀加速直线运动,然后刹车做匀减速直线运动,直到停止.如图2速度v和位移x的关系图像中能描述该过程的是哪一项.本题涉及汽车匀加速和匀减速过程中的v-x图像判断,对学生的图像分析、理解能力有一定的要求.再比如江苏高考中多次出现的用“微元思想方法”解决物理问题,很多学生都感觉到困难,一是因为用这种思想方法解决物理问题的意识不强,二是对这种思想方法不理解.可见要达到考纲中对数学思想方法的要求,不是一蹴而就的,需要在平时的教学过程中不断渗透.

图2
3 在高中物理教学中渗透数学思想方法有利于提升学生的素质
爱因斯坦曾经说:“这个世界可以由音乐的音符组成,也可以由数学的符号组成.”数学有如此威力,主要是其独特的思维和方法发挥作用.数学思想方法,是铭记在人们头脑中起永恒作用的数学观点和文化,数学的精神和态度.它使人思维敏捷,表达清楚,工作有条理;使人善于处世和做事,实事求是,锲而不舍;使人得到文化方面的修养,更好地理解、领略和创造现代社会的文明.饶汉昌先生等数学教育家撰文指出:“数学思想、方法是素质教育的重要内容”.在高中物理教学中渗透数学思想方法,不但具有即时价值,更具有延时价值,让学生学会直观判断、归纳类比、逻辑分析、建立模型、运用数据进行推断等强有力的思考方式.帮助学生更好地了解物质世界,使学生具有科学的精神、理性的思维和创新的本领;使学生充满自信和坚忍;使学生受益终身.例如在“闭合电路欧姆定律”的教学中,传统的教学模式都是通过能量守恒直接推出定律内容,但是如果我们在设计教学内容的时候能够和数学知识联系起来,让学生去探究其根源,相信学生更容易理解规律的内容及其本质.可以设计电路进行实验,让学生测出几组数据作U-I关系图,通过对图线进行分析,让学生得出作出的图线对应数学中的一次函数关系,从而得出图线的数学关系式,进一步讨论关系式中的物理量的含义,从而得出闭合电路欧姆定律.这种将物理问题转化为数学问题再还原为物理结论探究方式的有思想深度的课,不但使学生对知识的深刻理解,而且在以后的学习和工作中,他们可能把具体的数学知识忘了,但数学的思考问题的方法将永存.通过一些数学思想方法的渗透,让学生形成一种“数学头脑”,使他们在观察和提出问题、解决问题的每一个过程中,都带有鲜明的“数学色彩”,这样会具有真正的实效和长效,更有利于提升学生的素质.
4 在高中物理教学中渗透数学思想方法有利于培养学生运用数学方法研究物理问题的能力
数学和物理两学科具有密切的联系,数学对于物理学科来说,不仅仅是一种数量分析和运算的工具,更主要的数学是物理概念的定义工具、物理定律以及原理的表达和推导的工具.运用数学方法研究物理问题本身就是一种重要的抽象思维,因此,数学也是研究物理问题进行科学抽象和思维推理的工具.
4.1 培养学生运用数学方法表达物理过程、建立物理概念和规律的能力
概念和规律是物理的两条主线,物理概念是物理教学中一个重要的环节,物理概念是在实践的过程中思维抽象的结果,是高度抽象和主观的成果,但是当它实际运用的时候,就具有了具体、客观的内容.如何才能将抽象、主观变成具体、客观的内容呢,这就需要在数学思想的指引下,利用数学方法作为工具.因为数学是定义物理概念和表达物理规律的最简洁、最精确、最概括、最深刻的语言,许多物理概念和规律都要以数学形式(公式或图像)来表述.也只有利用了数学表述,才便于进一步运用它来分析、推理、论证,才能广泛地定量地说明问题和解决问题,才便于我们继续深入地去研究这个规律表面下蕴含的更多的物理意义.在错综复杂的物理问题中,正确运用数学思想方法可以让我们对物理规律的适用条件更充分地认识.
因此在研究物理现象的过程中,必须引导学生把实验观测和数学推导这两种手段有机地结合起来,以观察、实验的感性材料为依据,运用数学方法(包括公式和图像)来对其进行计算、分析、概括、推理,得出经验规律,并进一步抽象为物理定律.中学物理中的许多定律,例如牛顿第二定律、电阻定律、欧姆定律、楞次定律、气体实验定律等都是从实验出发,经过科学抽象为物理定律,最后运用数学语言把它表示为物理公式的.
4.2 培养学生应用数学知识进行定量分析、判断、推理、论证来解决物理问题的能力
抽象思维在物理学中很重要,而在物理学中进行抽象思维时,数学是不可缺少的非常有力的工具.它可使人们能从已知的物理定律或理论出发,利用数学的逻辑推理方法推导出新的规律或建立新的理论.例如,牛顿在开普勒行星运动规律的基础上,利用数学方法导出了万有引力定律.中学物理教学应该有计划地进行这方面的训练,培养学生推理、探索的能力和创新精神,从而提高他们的科学“预见”能力.例如,运用牛顿第二定律、运动学公式、功的公式推导动能定理,像这样既可以使学生获得新知识,又可以帮助他们领会物理知识间的内在联系.

图3

5 在高中物理教学中渗透数学思想方法有利于提高教师的教学水平
只有注重数学思想方法的渗透,才能把物理课讲活、讲懂、讲深.所谓“讲活”,就是让学生看到活生生的数学在处理物理中的应用过程,而不是死的数学结论,比如,小船渡河问题用数形结合思想进行讲解;所谓“讲懂”,就是让学生真正理解有关的数学内容在物理中的具体体现,而不是囫囵吞枣、死记硬背,比如匀变速直线运动中位移中点的速度和时间中点速度的比较,不是让学生记结论,学生只要学会了数学方法(如图像法)就会很快得出;所谓“讲深”,则是指使学生不仅能掌握具体的数学方法在物理中的应用,而且也能领会其内在的思想.比如对“微元法”不断的渗透学生就会领略“微元思想”,对“图像法”的不断渗透就会领略“图像思想”.总之,我们只有精心备课,有计划地将数学思想方法真正渗透于物理教学中,才能不断提高教学质量.当然,这也对教师从专业素养、教育理论、能力水平诸方面都提出了更高的要求.经过不断的实践总结,不但会提高我们的解题能力,更能使我们的教学水平得到很大的提高.
教育是慢的艺术.建构主义理论提出学生的认识必然有一个深化和发展的过程,就是说在物理教学中学生对一种数学思想方法的掌握不是一蹴而就的,是一个不断渗透的过程.杜甫的《春夜喜雨》中有“好雨知时节,当春乃发生,随风潜入夜,润物细无声”之句,希望教师们在教学中,有意识、有计划地将数学思想方法“化作春雨”滋润学生的物理心田.
1 杨振宁.爱因斯坦和二十世纪后半期的物理学[J].物理教学,1980.
2 徐卫兵.用“微元思想”突破概念难点教学[J].中学物理教学参考,2014(6):24-26.
3 徐卫兵.中学物理中的图象思想[J].中学物理,2012(5):49-52.

