一种利用修正牛顿迭代的时差定位算法
朱国辉,冯大政,李 进,周 延
(西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071)
一种利用修正牛顿迭代的时差定位算法
朱国辉,冯大政,李 进,周 延
(西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071)
针对传统基于迭代求解的时差定位算法中容易出现的发散问题,提出了一种新的基于修正牛顿迭代的时差定位算法.该算法首先利用辅助变量将非线性时差定位方程组转化为一组关于辐射源位置的伪线性方程,在此基础上把时差定位问题转化为约束加权最小二乘优化问题;然后,利用基于特征值修正的牛顿法进行定位解算,同时为了减少迭代次数,通过二次插值法对一维优化问题进行寻优求解,给出了迭代步长因子的求取过程;最后,通过仿真分析验证了所提算法的有效性.
无源定位;到达时间差;加权最小二乘估计;修正牛顿法;二次插值法
与传统的有源定位系统相比,无源定位技术具有隐蔽性强的优点,在雷达[1]、声纳[2]、无线通信和传感器网络[3]等领域有着广泛的应用.常用的无源定位技术包括基于到达时间、基于到达时间差和基于到达角的定位算法[4-7].基于多站时差的定位技术对接收系统的要求较低,具有定位成本低、精度较高等优点,因而受到越来越多的关注.
时差定位问题本质上是一个高度非线性估计问题,可用最大似然估计方法处理.在测量噪声服从高斯分布的前提下,最大似然估计将时差定位问题转化为非线性最小二乘求解问题,通常是利用迭代方法进行求解,且需要一个迭代初始值.目前常见的基于迭代求解的时差定位算法有泰勒级数法[8]、牛顿法[9]等,它们是一类需要初始估计位置的迭代算法,主要缺点是其收敛性非常依赖于目标函数的非线性程度和迭代初始值的精度.当用一组接近真实值的初始值进行迭代求解时,能够获得超线性乃至二次收敛速度[10],定位精度高.但是在初始值选择不好的情况下,迭代过程中容易落入到局部极小点,而且不能保证其收敛性.为此,笔者提出了一种新的基于迭代求解的时差定位算法.该算法首先通过对非线性时差定位方程进行转换,得到较规则的目标函数;然后在迭代过程中对海森矩阵进行特征值修正,在一定程度上避免了传统基于迭代求解的定位算法因矩阵奇异引起的发散现象,同时通过二次插值法求解迭代步长因子,有效减少了迭代次数.仿真结果验证了所提算法的有效性.
1 时差定位模型
辐射源u到接收站si的距离为

不失一般性,选取s1作为参考接收站,不考虑非视距传播的影响,可以得到时差定位方程为


其中,ni1=cΔti1,表示相应的距离差测量误差.令fi1(u)=ri-r1,将式(3)写成矢量形式为


最大化式(5),似然函数可以转换为极小化二次型目标函数[11],即

式(6)为关于辐射源位置的非线性目标函数,没有封闭解.
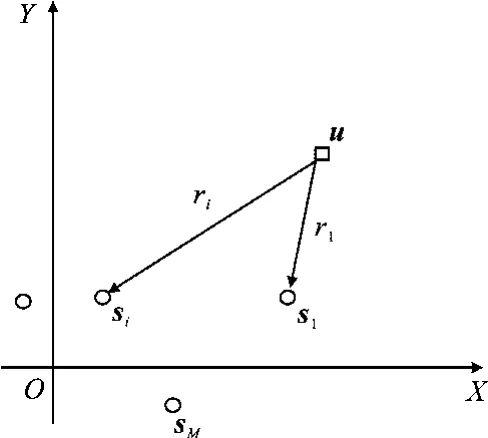
图1 无源时差定位示意图
2 基于修正牛顿迭代的时差定位算法
2.1 加权最小二乘估计
由式(1)可知,时差定位模型式(3)是关于目标位置的高度非线性函数,由此得到的目标函数式(6)的几何结构很不规则,并且存在局部极小点[12].为此,首先将时差定位问题转化为约束加权最小二乘问题,将式(3)右端的r1移至左端,两边同时平方,得

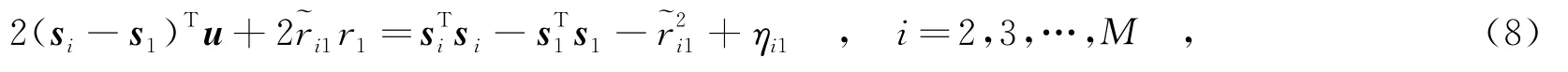

其中,η=2Bn,B=diag{r2,…,rM}.对近似方程Aθ≈b,进行加权最小二乘估计求解,可得


其中,g=[g2,…,gM]T.可在式(11)的基础上进行迭代求解.
2.2 基于修正牛顿迭代的时差定位算法

其中,Gu0和Hu0分别为目标函数在给定初始值u0下的梯度矢量和海森矩阵.将式(10)得到的结果作为初始值进行迭代,直到收敛.当初始值u0距极小点较远时,可能出现海森矩阵奇异的情形,此时不能确定下一步的迭代值;即使海森矩阵可逆,也可能是非正定矩阵,由此得到的搜索方向不一定是下降方向,如按式(12)进行迭代,目标函数值可能上升,这就导致算法失效.针对这些问题,提出一种基于特征值修正的牛顿法.
2.2.1 特征值修正


将矩阵Hu进行特征值分解得:Hu=UΛUT,其中,Λ=diag{ρ1,ρ2},U为相应的特征向量组成的矩阵.设ρ1和 ρ2已按从大到小的顺序排列,若ρ1和ρ2均为正数,则Hu为正定矩阵,取搜索方向若ρ1和ρ2均为负,取˜Λ=-Λ;若ρ2<0,取˜Λ=diag{ρ1,ρ1},则修正后的海森矩阵为修正后的海森矩阵的特征值均大于零,取搜索方向即为下降方向.给定任意迭代初始值,修正后的海森矩阵满足对称正定性.

2.2.2 步长因子λ的选取
引入迭代步长因子λ,使得每次迭代过程中,目标函数在下降方向上更接近极小值.一般来说,将代入目标函数使目标函数最小的λ即为所求.这种精确搜索往往需要进行迭代求解,计算量大,特别是当初始值远离最优解时,效率很低;而且很多优化算法的收敛速度并不依赖于精确的搜索过程.因此,提出了一种基于二次插值法的步长因子选取方法,令构造二次多项式p(λ)=a+bλ+cλ2,将其极小点作为φ(λ)真实极小点的近似.当λ=0时,令

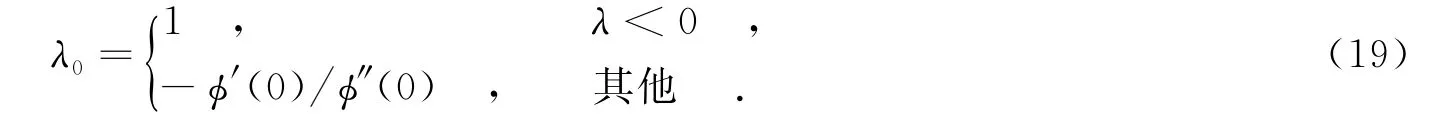
修正牛顿法的步骤如下:
(1)根据式(10)求取初始值u0,允许误差ε>0[12],令k∶=0.
(4)根据式(19)求取迭代步长因子λk.
3 性能分析
由于泰勒级数法和高斯牛顿法在实质上等价[12],为方便讨论,称基于目标函数的泰勒级数法为高斯牛顿法.为了检验文中算法对辐射源位置估计的性能,进行了下述的仿真实验,并将该算法与基于J(u)的泰勒级数法、基于的高斯牛顿法、牛顿法及克拉美罗界的仿真结果进行比较,各算法的迭代停止条件均为.假设有4个接收站参与定位,坐标分别为[20,1]T,这里及下面仿真实验中的辐射源坐标单位均为米.噪声协方差矩阵Q是对角线元素为非对角线元素[13]为的对称矩阵.采用位置估计的均方根误差对各算法的定位性能进行衡量,其定义式为

仿真1辐射源位置坐标为[10,30]T,x∈[-100,100],y∈[-100,100].取(4BQBT)-1.图2(a)~(c)分别给出了目标函数J(u)在权W0及目标函数在权W0和最优权W1下随x和y变化的函数取值示意图.从图2(a)可以看出,目标函数J(u)的几何结构很不规则,这就对迭代初始值的选取要求很高,用传统优化算法进行迭代求解时较难得到正确结果.从图2(b)和图2(c)可以看出,目标函数)在权W0和最优权W1下的几何结构相似,在y轴方向上较为平坦,但避免了局部极小点,与图2(a)相比有很大改善,几何结构较为规则,能较易收敛到正确的结果,这也在下面的仿真中得到验证.

图2 目标函数J(u)及随x和y变化的函数取值示意图
仿真2近场辐射源位置坐标为[20,12]T,噪声功率从10-3.5变化到101.2,将式(10)所得结果作为各算法的迭代初始值.图3(a)和图3(b)分别为各算法随噪声功率变化的平均迭代次数和均方根误差的统计结果,式(11)中W=W0.从图3(a)和图3(b)可以看出,在噪声功率较小时,各算法对辐射源位置估计的均方根误差均接近克拉美罗界,所需平均迭代次数也相当.随着噪声功率的增加,泰勒级数法的平均迭代次数保持最小,但其估计均方根误差迅速增加,而文中算法并没有出现性能急剧下降的现象,定位精度与高斯牛顿法、牛顿法相当,说明了目标函数具有较好的几何结构.但高斯牛顿法和牛顿法理论上仍然存在发散的可能性.文中算法的单步迭代计算量要小于高斯牛顿法和牛顿法的计算量,但从图3可以看出,当噪声功率较大时,迭代次数要明显小于它们.最后,文中算法、高斯牛顿法和牛顿法的均方根误差会出现低于克拉美罗界的现象,这是因为在测量误差较大时,式(7)中的高阶误差项不能忽略不计,这时各算法是有偏估计的,而克拉美罗界是所有无偏估计所能达到的下界.
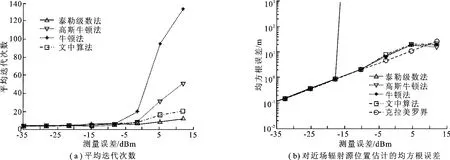
图3 各算法对近场辐射源位置的定位性能示意图
仿真3远场辐射源位置坐标为[300,220]T,噪声功率从10-6变化到10-2,各算法迭代初始值的选取同仿真2.图4(a)和图4(b)分别给出了各算法对远场辐射源位置估计随噪声功率变化的平均迭代次数和均方根误差的统计结果.从图4(a)和图4(b)可以得出与仿真2类似的结论,在噪声功率较小时,各算法对辐射源位置估计的均方根误差均接近克拉美罗界.基于目标函数J(u)的泰勒级数法平均迭代次数较少,但是随着测量误差的增加,其均方根误差迅速增加.而基于目标函数的文中算法并没有出现性能急剧下降的现象,迭代次数要明显小于高斯牛顿法和牛顿法的迭代次数,定位精度稍优于高斯牛顿法的定位精度,这是因为高斯牛顿法等价于目标函数的一阶近似.最后,文中算法、高斯牛顿法和牛顿法的均方根误差会出现类似于仿真2中低于克拉美罗界的现象,原因同仿真2中的说明.

图4 各算法对远场辐射源位置的定位性能示意图
4 结束语
针对传统基于迭代求解的时差定位算法中出现的发散问题,提出了一种基于修正牛顿迭代的时差定位算法.通过引入辅助变量将高度非线性定位问题转化为约束加权最小二乘问题,求取较规则的目标函数,并在此基础上利用修正牛顿法进行迭代求解.所提算法一方面采取特征值修正避免了传统迭代算法因矩阵奇异出现的发散问题,另一方面采用二次插值法求取迭代步长因子减少了迭代次数,具有较好的定位性能.当测量误差较大时,文中算法忽略了高阶误差项对均值和其他统计特性带来的影响.如何根据高阶误差项的统计特性进行更好的定位,是今后研究的方向.
参考文献:
[1]Min Jiang,Niu Ruixin,Blum R S.Bayesian Target Location and Velocity Estimation for Multiple-input Multiple-output Radar[J].IET Radar,Sonar and Navigation,2011,5(6):666-670.
[2]Fluckiger M,Neild A,Nelson B J.Optimization of Receiver Arrangements for Passive Emitter Localization Methods [J].Ultrasonics,2012,52(3):447-455.
[3]Gholami M,Cai Ningxu,Brennan R W.Evaluating Alternative Approaches to Mobile Object Localization in Wireless Sensor Networks with Passive Architecture[J].Computers in Industry,2012,63(9):941-947.
[4]牛新亮,赵国庆,刘原华,等.低空目标高精度无源时差定位方法[J].西安电子科技大学学报,2009,36(5):862-866.
Niu Xinliang,Zhao Guoqing,Liu Yuanhua,et al.High Precision Passive TDOA Location Method for Low-altitude Targets[J].Journal of Xidian University,2009,36(5):862-866.
[5]Annibale P,Filos J,Nyalor P,et al.TDOA Based Speed of Sound Estimation for a Temperature and Room Geometry Inference[J].IEEE Transactions on Audio,Speech,Language and Signal Processing,2013,21(2):234-246.
[6]Cheung K W,So H C.A Multidimensional Scaling Framework for Mobile Location Using Time-of-arrival Measurements [J].IEEE Transactions on Signal Processing,2005,53(2):460-470.
[7]同非,王俊,李红伟.Memetic优化的外辐射源雷达方位-多普勒定位方法[J].西安电子科技大学学报,2012,39(4): 46-51.
Tong Fei,Wang Jun,Li Hongwei.Novel Passive Radar Location Algorithm Based on Memetic Optimization by Using the Bearing-and-Doppler Frequency[J].Journal of Xidian University,2012,39(4):46-51.
[8]Foy W H.Position-location Solution by Taylor-series Estimation[J].IEEE Transactions on Aerospace and Electronic Systems,1976,12(2):187-194.
[9]Liu Ying,Zhang Xu,Liu Dan,et al.Study of Location Algorithm for Wireless Sensor Networks Based on Newton Iteration[J].Advanced Materials Research,2013,645:285-289.
[10]袁亚湘,孙文瑜.最优化理论与方法[M].北京:科学出版社,1997.
[11]Torrieri D J.Statistical Theory of Passive Location Systems[J].IEEE Transactions on Aerospace and Electronic Systems,1984,20(2):183-198.
[12]Dogancay K,Sakhtsari A H.Target Tracking by Time of Difference of Arrival Using Recursive Smoothing[J].Signal Processing,2005,85(4):667-679.
[13]Chan Y T,Ho K C.A Simple and Efficient Estimator for Hyperbolic Location[J].IEEE Transactions on Signal Processing,1994,42(8):1905-1915.
(编辑:齐淑娟)
简 讯
近日,在“2014年英特尔杯嵌入式系统专题邀请赛”中,西安电子科技大学应邀参赛的4支代表队全部获奖.其中,“基于视觉体感双平衡的防晕动系统”夺得本次大赛的最高奖项“Intel杯”.嵌入式系统专题邀请赛自2002年举办首届竞赛以来,到2014年已成功举办了七届.今年共有来自15个国家和地区的83所高校,170支队伍参加.我校另三支参赛队分获二、三等奖.
(摘自《西电科大报》2014.8.14)
TDOA location algorithm based on modified Newton iterations
ZHU Guohui,FENG Dazheng,LI Jin,ZHOU Yan
(National Key Lab.of Radar Signal Processing,Xidian Univ.,Xi’an 710071,China)
For the divergence problem of traditional iterative process based location algorithms,a new modified Newton algorithm for the passive location from time differences of arrival(TDOA)is proposed. The proposed algorithm firstly reorganizes the nonlinear TDOA equations into pseudo-linear ones by using an auxiliary parameter,and a constrained weighted least-squares minimization is developed for the positioning problem instead of the Maximum Likelihood estimator.A modified Newton method based on eigenvalue modification is then applied to obtain the emitter position.In order to reduce the number of iterations,an appropriate iteration step size is computed via one-dimensional optimization by the quadratic interpolation method.Simulation results demonstrate the effectiveness of the proposed algorithm.
passive location;time difference of arrival;weighted least squares estimates;modified Newton algorithm;quadratic interpolation method
TN97
A
1001-2400(2014)05-0036-06
2013-06-24< class="emphasis_bold">网络出版时间:
时间:2014-01-12
国家自然科学基金资助项目(61271293)
朱国辉(1987-),男,西安电子科技大学博士研究生,E-mail:zhugh@stu.xidian.edu.cn.
http://www.cnki.net/kcms/doi/10.3969/j.issn.1001-2400.2014.05.007.html
10.3969/j.issn.1001-2400.2014.05.007

