基于高光谱影像的流形学习降维方法近邻畸变分析

张辉远

(中铁第四勘察设计院集团有限公司，湖北武汉 430063)

基于高光谱影像的流形学习降维方法近邻畸变分析

张辉远

(中铁第四勘察设计院集团有限公司，湖北武汉 430063)

为了验证高光谱遥感影像数据经流形学习方法降维后数据之间关系的变化，提出了一种新的流形学习降维效果评估方法：近邻畸变参数分析。该方法简单直观，不需先验知识，能直观显示降维后数据在地理空间中产生的变化，通过参数统计显示降维效果的好坏。

流形学习 高光谱遥感 降维 评估

高光谱分辨率遥感是采集和处理可见光、近红外以及短波热红外波段范围内窄波段“连续”电磁光谱信息的遥感成像及分析技术。目前，高光谱遥感领域已形成了由地面测量到星载平台的完整观测体系，是国家地理国情监测的重要数据来源。但是光谱维度观测的大幅提升加重了其处理过程的存储负担与计算复杂度，其中非线性的相关性特征更降低了传统高光谱遥感影像数据分析的精度。高光谱遥感影像的降维，尤其是非线性降维方法是解决这些问题的必要手段，也是目前遥感数据解译领域的研究热点问题之一。

流形学习方法是一种新型的非线性降维方法，已在模式识别领域建立了完整的理论体系，取得了丰富的应用成果，在遥感土地覆盖与利用中的应用也越来越多。流形学习算法降维效果的评估是实践流形学习方法的一个重要环节。好的评估方法不仅可以检验具体流形学习算法模型的特征提取能力，也能为流形学习算法参数的选择提供必要参考。目前，针对流形学习特征提取算法的研究中涉及降维效果评估方法的研究内容不多。标准化模型数据演算方法评估流形学习算法的降维效果是最常用的方法，该类方法能直观反映理想状况下流形学习算法模型提取非线性特征的能力，但是无法验证在真实数据集(如高光谱遥感影像)上流形学习算法模型的降维效果。由于流形学习方法将嵌入在高维空间中的非线性空间投影到低维的欧式空间中，以欧式距离为度量的聚类方法成为了检验流形学习方法在真实数据集上降维结果的自然选择。Mohan[1]使用局部线性嵌入方法与等角特征映射算法对AVIRIS影像降维时采用K近邻聚类方法对降维结果进行聚类分析；Talwalkar等[2]采用K均值聚类算法分析流形学习方法在CMU-PIE与Webfaces-18M脸谱数据库上的降维效果，优化了评价聚类精度的参数；最终通过精确度(Accuracy)与纯净度(Purity)两个参数衡量流形学习算法的降维效果。Kokiopoulou等[3]、曾恒等[4]以及徐蓉等[5]同样采用聚类方法验证在脸谱数据库、笔迹数据库、语音数据库等各类真实数据集中流形学习算法的降维效果。聚类方法虽然能够较好的反映低维欧式空间中数据的分布规律以及离散程度，但是其初始参数较多，无法保证算法收敛等问题，使其难以保证评估结果的一致性。使用聚类方法对流形学习降维效果的评估必须建立在具备测试数据先验知识或标记(labeled)的基础上，这些因素导致聚类方法在解决高光谱遥感影像降维效果评估时存在局限性。

提出一个基于高光谱遥感影像的流形学习降维效果评估方法。该方法利用遥感影像图谱双重性的特点，采用近邻畸变参数衡量流形学习降维前后对影像特征的影响，该方法仅需少量预设参数，在无先验知识的前提下能取得与聚类评估方法相似的评估结果。

1 流形学习算法原理与分析

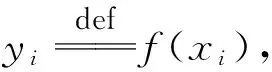
等角特征映射法利用流形极小邻域满足欧式空间性质这一特点求算原数据集中任意两点间测地线距离，并通过多位排列方法(Multi-dimensional Scale)在低维空间中找到一组数据集，使其任意两点间相对距离关系与原始数据集中两点测地线距离关系一致，从而得到原始数据集非线性特征在低维欧式空间中的表达。为了得到两点间测地线距离，只需设定原始数据空间中任意点的近邻大小，并有

其中xi与xj为原始空间中任意一点，Ki为xi的近邻集合，dij为xi与xj的距离。以dij为边长建立原始数据点的距离图，并计算点间在距离图上的最小距离既为两点之间的测地线距离。

拉普拉斯特征映射算法同样也是寻求原始数据集的非线性特征与低维欧式空间的等角映射。但是，等角特征映射方法利用测地线距离保留全局特征，而拉普拉斯特征映射算法则寻求在局部保持空间点与近邻点几何关系的同胚映射。拉普拉斯特征映射算法同样需构件近邻关系，并建立权阵

目前在以上两种方法的基础上衍生出的流形学习算法模型逐日增多。但是，如前文中所述，在使用一个流形学习方法模型时，必须对其基本参数进行设置，如输入数据点的近邻集大小等。因此，一个可靠且便捷的流形学习算法评估模型是使用流形学习算法时的必要工具。

2 利用近邻畸变参数评估流形学习算法降维效果

对于一个理想的特征提取方法，其降维结果中性质相同的点间分布更密集，距离更近；而性质不同的点间分布更稀疏，距离更远，这也是使用聚类方法评估流形学习算法降维效果的依据。对于高光谱遥感影像而言，其在谱空间降维后的变化也能体现在地理空间中，即经过特征提取降维后，高光谱遥感影像中性质相同的像素之间差异应当变小，性质相异的像素之间差异应当变大。

近邻畸变参数则利用高光谱遥感影像这种图谱二重性的特点，通过检验在地理空间上，降维后数据的点间相关性变化来反映其在光谱空间中的变化。如图1，高光谱遥感影像中任意像素a，对应原光谱空间中的向量Va以及降维后的嵌入空间中的向量Va。令{bi}(i=1,2,…,n)为a在影像中的n个邻像元集，并对应光谱空间中的向量集{Vbj}以及降维后的嵌入空间中的向量集{Vbj}。则像素a的近邻畸变参数为

(1)

其中ωi为权重系数，即像素a相邻像素bi的相关系数距离变化占像素a近邻畸变参数的比例；根据具体情况的不同，可选择不同的相邻像素窗口大小以及权重系数的分布。当相邻像素窗口为1阶窗口时(即3×3窗口)，ωi的选择通常有如图2中的三种方式：式(1)中的corr(·,·)为向量间的相关性系数。由于流形学习算法过程中的归一化过程，像元间的一些度量关系会有较大的变化。例如：因缩放关系，降维后像元间的欧式距离单位往往和原空间相差很远(如图1右上图中，向量元素的最大值不超过1，而图1右下图中，降维后的向量元素取值区间在-50到10之间)；同样，由于平移变化，降维后空间原点位置往往改变很大，因此光谱角投影距离也无法用于比较降维前后空间点分布的变化关系。相关系数距离是唯一能衡量高维空间中点间关系相对变化关系的度量。

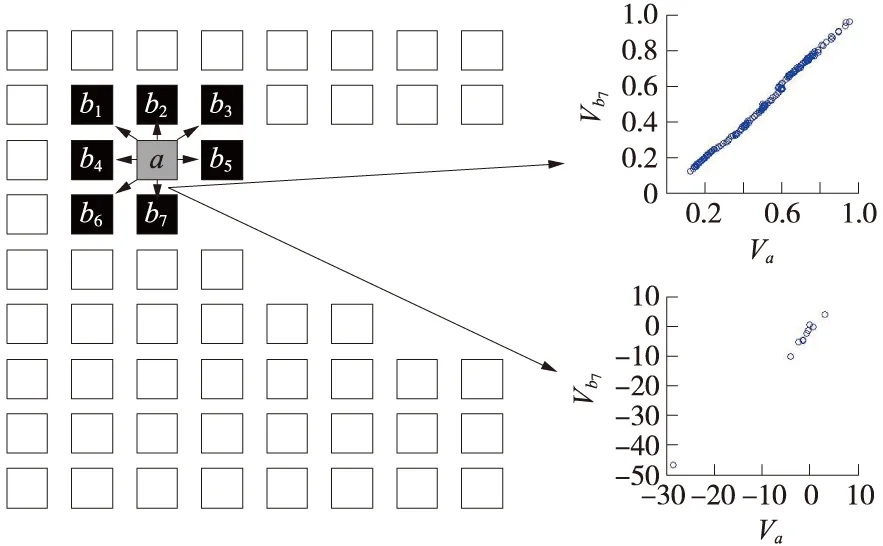
图1 近邻畸变参数原理

图2 近邻畸变参数中权重系数的分布方法

3 近邻畸变试验与分析

在流形学习算法降维效果评估实验中，采用了Indian Pine 数据集。该数据集截取于AVIRIS机载高光谱成像传感器在美国印第安纳州获取的影像，是最常用的基准测试数据集之一。该影像的空间分辨率为30 m，影像大小为145像素×145像素， 共21 025个高光谱数据点。该影像包含由400到2 500 nm共220个有效波段，在去掉水气吸收带与噪声较大的波段，保留有158个波段，该数据集主要覆盖农业用地。如图3所示，图3(a)为高光谱影像假彩色图，该影像包含158个光谱波段，并利用FLAASH大气校正模型得到每个波段的反射率值。图3(b)为流形学习算法降维后得到的由近邻畸变参数构成的灰度图，颜色由白至黑代表近邻畸变程度由低变高。图3(c)为以像素近邻畸变参数值为Z轴，影像空间坐标为X，Y轴的近邻畸变参数三维重建图。通过计算整幅影像的近邻畸变参数，可以直观的得到高光谱遥感影像降维前后在地理空间邻近像素之间发生的变化。

通过图3(b)和3(c)，可以直接观察到高光谱影像降维后与原始影像相比发生的变化。在影像中不同地物邻接区域内产生了较大的畸变；而在同类型地物内部，则畸变小，且畸变程度相同。这符合前文中对特征提取方法降维结果的分析，即：性质相同的点间分布更密集，距离更近；而性质不同的点间分布更稀疏，距离更远。性质不同的像素点多分布于影像中不同地物的边缘，而性质相同的像素点分布于同一地物内部。为了区分这两种变化，引入一个边缘掩膜分割近邻畸变参数结果，该边缘掩膜即可通过边缘提取算法获得，如canny算子、sobel算子等；也可通过人工操作从影像中标注出地物的边缘信息。掩膜内部像素上的畸变参数为良性近邻畸变，掩膜外部像素上的畸变参数为恶性近邻畸变参数。通过对良性近邻畸变参数和恶性近邻畸变参数的统计分析，可以得到特征提取方法降维结果的定量数值。良性近邻畸变参数均值越高则表明特征提取方法提取特征的能力越强，反之则越弱；而恶性近邻畸变参数均值越高则表明特征提取方法保留原有数据信息的能力越弱，反之则越强。

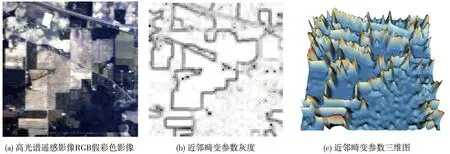
图3 近邻畸变参数

本实验分别考察了本征纬度(即降维后数据集的维数)，最小近邻大小，以及采用度量方法对流形学习算法降维效果的影响。在图4的每个分图中，由上自下分别为使用欧式距离时的良性畸变，使用光谱角度量时的良性畸变，使用欧式距离时的恶性畸变，以及使用光谱角度量时的恶性畸变。四个分图由(a)至(d)，分别为本征维数变化时等角特征映射算法的近邻畸变变化，最小近邻数变化时等角特征映射算法的近邻畸变变化，本征维数变化时的拉普拉斯特征映射算法的近邻畸变变化，以及最小近邻数变化时的拉普拉斯特征映射算法的近邻畸变变化。

其中，使用光谱角度量时的近邻畸变整体要小于欧式距离；等角特征映射算法的良性畸变参数与拉普拉斯特征映射算法基本相同，但拉普拉斯特征映射算法的恶性畸变参数要小于等角特征映射算法。随着本征维度的上升，两种算法的近邻畸变参数同样会升高，等角特征映射算法的近邻畸变参数始终随着本征维度的上升而升高，而拉普拉斯特征映射算法的近邻畸变参数在本征维度超过15以后上升幅度趋缓。当原数据近邻数小于5时，两种流形学习算法的近邻畸变参数都有明显的下降。从实验结果可以看出，近邻畸变参数的变化与流形学习原理联系紧密。例如，由于拉普拉斯特征映射算法更注重保留局部信息，因此能得到跟低的恶性畸变参数；并且拉普拉斯特征映射采用热核函数估算数据点间关系，距离较远的点间权重极小，因此该算法受近邻数量设置影响较小。

图4 流形学习方法的近邻畸变参数分析

4 结束语

提出了一种新的评估流形学习降维效果方法，利用该方法并结合高光谱遥感影像，即可直观的显示流形学习方法在降维前后对遥感数据地理空间上的影响，也能通过参数统计反映降维方法对数据的影响的定量统计。

[1] A. Mohan, G. Sapiro, and E. Bosch, “Spatially Coherent Nonlinear Dimensionality Reduction and Segmentation of Hyperspectral Images,” IEEE Geosci. Remote Sensing Lett., 2007，4：206-210

[2] A. Talwalkar, S. Kumar, and H. Rowley, “Large-scale manifold learning,” presented at the Computer Vision and Pattern Recognition, 2008. IEEE Conference on, pp. 1-8

[3] E. Kokiopoulou and P. Frossard, “Semantic Coding by Supervised Dimensionality Reduction,” Multimedia, IEEE Transactions on, 2008，10(5)：806-818

[4] 曾恒.流形学习在高速列车安全性态评估数据分析中的应用[D].成都：西南交通大学,2007

[5] 徐蓉.流形学习概述[J].智能系统学报，2006(1)

[6] 殷兴青，韩岩，张忠良.遥感融合影像在摄影测量应用中的质量评价[J].铁道勘察,2008(6)

[7] 余峰，余洁，简骁.基于Hough变换的高分辨率遥感影像道路提取方法研究[J].铁道勘察,2011(5)

[8] 谭伟.基于图像的铁轨缺陷检测系统的算法研究及软件设计[D].大连：大连海事大学,2004

[9] 李渝勤，孙丽华.基于规则的自动分类在文本分类中的应用[J].中文信息学报,2004(4)

[10]郑丽，潘建平.基于数学形态学的遥感图像道路提取[J].铁道勘察,2010(1)

AnalyzeofManifoldLearningDescendingDimensionMethodNeighbourDistortionDependonHyperspectralVideo

ZHANG Hui-yuan

2014-01-21

张辉远(1961—)，男，1982年毕业于上海铁道学院铁道工程专业，高级工程师。

1672-7479(2014)02-0037-04

P237

： A