基节误差作用下少齿差行星齿轮轮齿载荷分析

刘斌彬

（福建工程学院 机械与汽车工程学院，福建 福州 350108）

在少齿差行星齿轮传动中，理论啮合线附近的齿对齿廓面间的间隙γ非常小，若齿轮副受载较大而产生的较大的弹性变形时，间隙γ将消失，形成多对齿接触共同承担载荷的情况，齿轮副的实际承载能力提高.前苏联的YASTREBOV最早预言了上述现象，张文照等［1］通过对少齿差齿轮副进行应变试验确实观测到了该现象，但并未给出载荷在各齿对间的分配比例计算方法.考虑到制造误差相对上述间隙γ较大，若计入误差，则间隙γ将发生不小的变化，齿轮副啮合时实际同时接触承载的齿对数将发生变化.黄霞等［2］通过多元回归分析认为齿轮的基节误差是影响间隙γ的最重要因素.应广驰等［3］建立了多对齿啮合时载荷分配的数学模型，但对误差的处理只简单校核单齿对啮合时的弯曲静强度.

因此，为充分发挥少齿差行星齿轮传动应有的承载能力，必须建立考虑基节误差的载荷分配数学模型.

1 基节误差及载荷分配数学模型

轮齿间的基节误差服从正态分布［4］，且相互独立.根据3σ准则（σ代表标准差），可得基节误差的期望μfpbi和标准差fpbi：

式中：fpb为基节极限偏差.

现将内外齿轮中各轮齿及啮合线附近的齿对按图1所示进行编号.各齿对编号为Lc（c＝0，1，2，…，n），处于理论啮合线上的齿对为L0；内齿轮各轮齿编号为i（图中3≤i≤z2－3）（z2为内齿轮齿数）；外齿轮各轮齿编号为j（3≤j≤z1－3）（z1为外齿轮齿数）；Lc，（i，j）表示由内齿轮上轮齿i及外齿轮上齿轮j所构成的齿对，编号为Lc.

图1 少齿差齿轮副示意图Fig.1 Schematic diagram of the small teeth difference planetary gear transmission

图中ra2，ra1分别为内外齿轮的齿顶圆半径；rf2，rf1分别为内外齿轮的齿根圆半径；r2，r1分别为内外齿轮的分度圆半径；O2，O1分别为内外齿轮的中心；a′为两个齿轮的中心距.

基节误差将导致各齿对Lc（c≠0）齿廓面间的相对位置发生改变，其变化量ec可以用式（2）计算［2］：

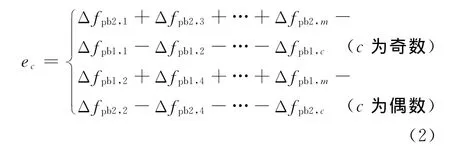
式中：Δfpb2，c，Δfpb1，c为 内 外 齿 轮 相 应 轮 齿 的 基 节误差.

齿轮副受载产生弹性变形，根据相对运动，若假定内齿轮固定，外齿轮将产生逆行星轮自转方向的附加转角θc.若弹性变形足够，转角θc将填补原有齿廓工作面间的理论间隙角φc、由弹性变形所引起的转角φδc及齿廓面间位置偏差ec引起的转角φec，即：

其中，弹性变形所引起的转角φδc可由下式计算得到：

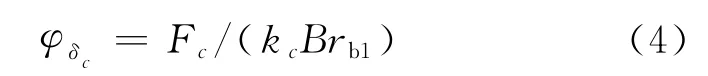
式中：Fc，kc分别为齿对Lc所承担的法向载荷和法向刚度；B为齿轮的接触宽度；rb1为外齿轮的基圆半径.

位置偏差ec引起的转角φec为

对于外齿轮，应有：

将式（3）—（5）代入式（6）并化简，得：

注意到齿轮副承担的总载荷F应为各齿对承受的载荷Fc之和，即

将式（7）与式（8）联立，即得：

求解该矩阵方程即得齿轮副在某时刻啮合时同时接触承载的齿对数n以及载荷在各接触齿对间的分配情况.引入弹性载荷比例系数Kc，（i，j）来反映接触齿对Lc，（i，j）实际所承担载荷的比例：

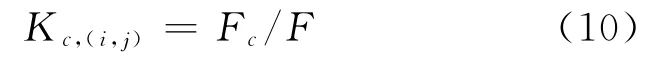
为验证该模型的正确性，现以某参数齿轮副为例，参数见表1，加工精度为7级，建立有限元模型［5］如图2，分别对大量不同的误差组通过有限元模型以及式（9）分别进行计算，图3所示为其中的8组误差的计算结果.

从图3可以看出，在不同误差作用下，无论是同时接触承载的齿对数n还是载荷在各齿对间的分配情况，两模型相差不大，表明本文所建立的载荷分配数学模型具有较高的可靠性.

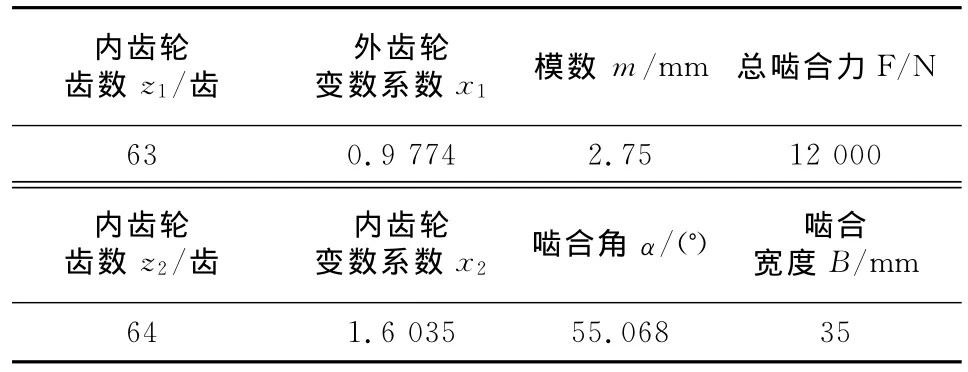
表1 某少齿差齿轮副主要参数Tab.1 Main parameters of a small teeth difference planetary gear

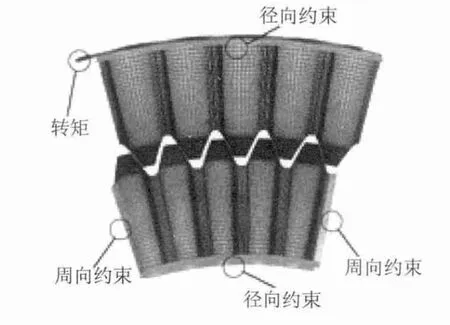
图2 齿轮副啮合有限元模型Fig.2 Finite element model of a small teeth difference planetary gear transmission

图3 有限元模型与数值模型对应齿轮副承载情况Fig.3 Bearing situation of Gear pair in finite element model and mathematical model

2 用蒙特卡罗方法分析基节误差

基节误差属于随机制造误差，为分析其对某参数齿轮副承载时同时啮合齿对数及载荷在各啮合齿对间分配情况的影响，必须对大量不同的随机误差进行计算并统计，为此可引入蒙特卡罗（MC）方法.MC法即统计模拟方法，即对已知的数学模型的有关变量按其概率分布进行抽样计算并统计结果，随机样本越多，结果越准确［6］.

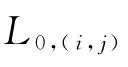
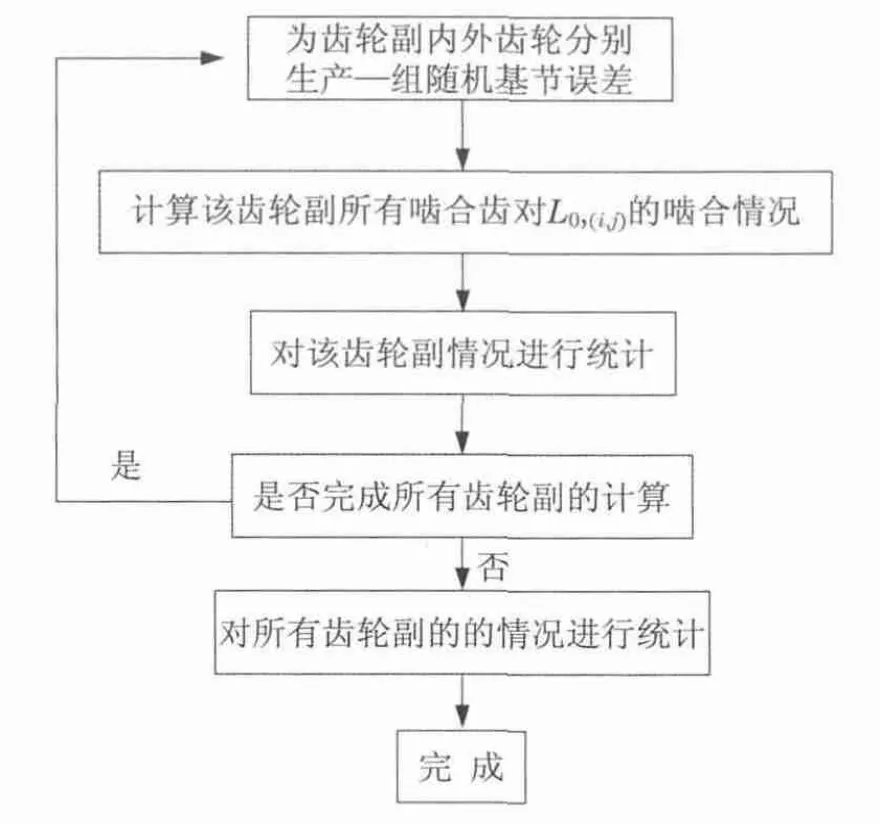
图4 MC法流程图Fig.4 Flowchart of Monte Carlo method

2.1 单个齿轮副的啮合情况分析

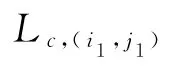
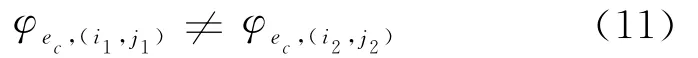
式中：j为外齿轮轮齿编号；Δz为内外齿轮齿数差.

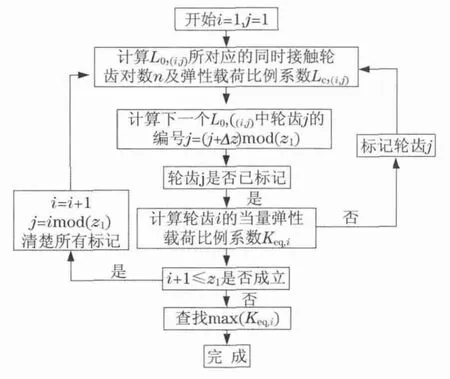
图5 内齿轮啮合情况分析流程图Fig.5 Analysis flowchart of gear pair meshing

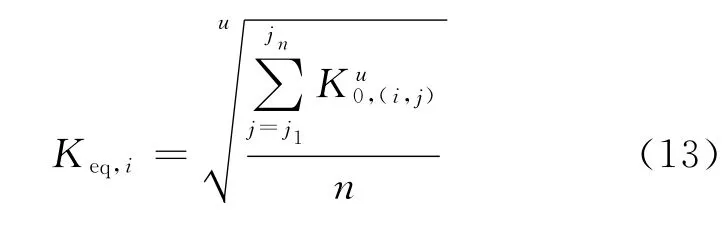
式中：u是材料指数.

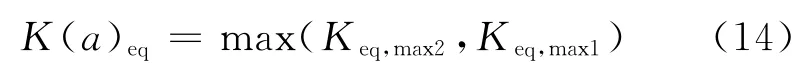
2.2 大量齿轮副的分析

采用上述的算法，遍历大量具有随机分布基节误差的齿轮副an，对其进行分析，计算各齿轮副的当量载荷系数K（a1）eq，K（a2）eq，…，K（an）eq，而后对这些数值进行统计，得到其概率曲线，设计时按可靠度代入齿根弯曲应力计算公式中.

3 实例

以某少齿差行星齿轮减速器为例进行说明，通过MATLAB软件生成2500对具有随机分布基节误差的齿轮副，图6为某齿轮副a内外齿轮各齿基节误差的具体数值.

图6 某齿轮副a的基节误差分布图Fig.6 Base section error distribution of one gear pair

通过图4所示的算法对2 500对齿轮副进行计算并统计，结果如图7，8所示，其中KPeq，max为内外齿轮相应的最大当量载荷系数.

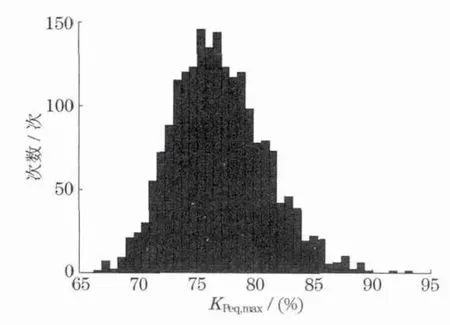
图7 齿轮副K（a）eq的分布直方图Fig.7 K（a）eq distribution histogram of gear pairs

图8表明，可靠度为99%的设计当量载荷系数K（a）eq为86.53%，即该参数齿轮副在啮合时理论啮合轮齿L0实际承担的载荷占总载荷的比例可按85.83%等效计算.而在不考虑基节误差的情况下，该值仅为49.53%，可见基节误差对齿轮对实际承担载荷的影响很大.实际啮合过程可能出现两种极端：①少数轮齿误差较大使得各轮齿间隙加大，啮合时出现单齿对完全承载，图9为某误差下的有限元仿真结果，可以看到载荷仅由一对齿轮承担；②误差抵消了部分齿廓间隙，齿廓间隙减小，同时接触的齿对数增加.图10为某误差下的有限元仿真结果，可以看到出现5对齿同时接触承载.

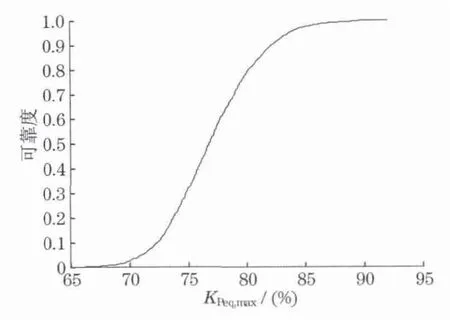
图8 齿轮副K（a）eq的概率曲线Fig.8 K（a）eq probability curve of gear pairs

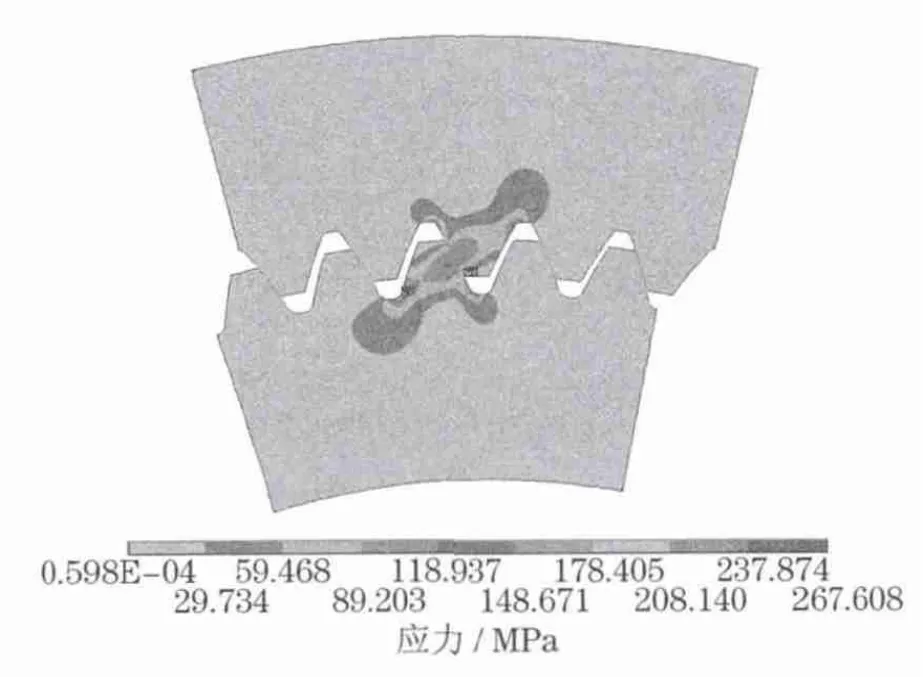
图9 单对齿啮合承载的情况Fig.9 Situation of bearing load by a single pair of teeth

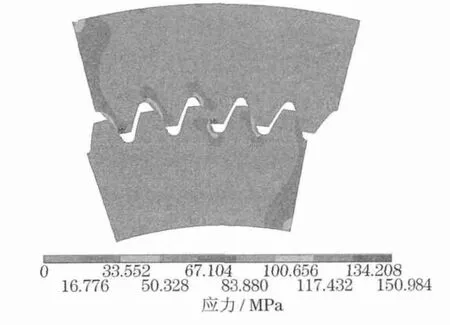
图10 5对齿接触承载的情况Fig.10 Situation of bearing load by five pairs of teeth

4 结论

本文建立了考虑基节误差的载荷分配数学模型并通过有限元仿真验证了该模型的正确性；将蒙特卡罗方法引入到载荷分配模型中分析了基节误差对少齿差行星齿轮啮合情况的影响，并给出了分析的流程和算法.结果表明：计入基节误差后少齿差行星齿轮传动的实际承载能力将较理想情况有一定的下降，故应考虑基节误差的影响.

［1］张文照，王光华.渐开线少齿差内啮合同时接触齿数研究及实际重合度的一种计算方法［J］.上海化工学院学报，1980（1）：92－100.

ZHANG Wenzhao，WANG Guanghua.An investigation into the number of contact-teeth for a pair of involutes internal meshing gears with small difference between their teeth num and one calculating method for the virtual contact ratio［J］.Journal of Shanghai Institute of Chemical Technology，1980（1）：92－100.

［2］黄霞，谢永春，李润方，等.误差对直齿内啮合传动重合度的影响分析［J］.机械研究与应用，2004，17（6）：33－37.

HUANG Xia，XIE Yongchun，LI Runfang，et al.Analysis for the effects of errors on the internal gearing spur gear transmission［J］.Mechanical Research ＆ Application，2004，17（06）：33－37.

［3］应广驰，张策，宋轶民，等.三环传动的弹性啮合、载荷分配和强度计算［J］.机械设计，2004，21（8）：12－14.YING Guangchi，ZHANG Ce，SONG Yimin，et al.Elastic meshing，load distribution and strength calculation of three-ring transmission［J］.Journal of Mechanical Design，2004，21（8）：12－14.

［4］庞庆，柏永新.圆柱齿轮加工误差分布规律的研究［J］，机械传动，2004，28（1）：7－9.

PANG Qing，BO Yongxin.Study on distribution rules of machining errors of cylindrical gears［J］.Journal of Mechanical Transmission，2004，28（1）：7－9.

［5］叶先磊，史亚杰.ANSYS工程分析软件应用实例［M］.北京：清华大学出版社，2003.

YE Xianlei，SHI Yajie.Application examples of ANSYS engineering analysis software ［M］.Beijing：Tsinghua University Press，2003.

［6］徐钟济.蒙特卡罗方法［M］.上海：上海科学技术出版社，1985.

XU Zhongji.Method of Monte Carlo［M］.Shanghai：Shanghai Science and Technology Press，1985.