高压电机定子线棒两电极介质损耗因数与电容关系的研究
胡 波,梁智明,漆临生,周 进,张小俊, 何海洋,黄绍波
(东方电气集团东方电机有限公司,四川德阳 618000)
高压电机定子线棒两电极介质损耗因数与电容关系的研究
胡 波,梁智明,漆临生,周 进,张小俊, 何海洋,黄绍波
(东方电气集团东方电机有限公司,四川德阳 618000)
对高压电机定子条式线棒的槽部与端部进行了绝缘结构和防晕结构分析。首次建立了线棒槽部与端部的两电极介质损耗因数及对地电容的电路模型,同时使用两电极测试方法分别测试并分析了电极长度与外施电压对整体性良好线棒与严重脱壳线棒的介质损耗因数和电容的影响。计算得到了介质损耗因数与电容的数值关系,为高压电机整机介质损耗因数的计算提供了理论支撑与试验依据。
高压电机;定子线棒;两电极;介质损耗因数;电容
0 引言
近二十年来,国内制造厂引进、消化、吸收了很多国外电机定子线棒与整机绕组的新技术,推广使用了很多新型绝缘材料、新绝缘结构或制造工艺,大大提高了线棒绝缘的电气及机械性能。部分厂的线棒绝缘已接近或达到了世界先进水平。
尽管多年来国内多胶模压或少胶真空压力浸渍(VPI)的单只成型线棒绝缘的介质损耗因数测试及其考核标准已按照国内外标准执行,很大程度上能够检测出了线圈绝缘内部微气隙,但仍然无法完全避免少量气隙在运行电压下的局部放电可能引起电、化学、机械、光、声等多因子老化。这会加速定子绕组在运行过程中的绝缘老化,进而缩短定子线棒绝缘的寿命。而采用整体真空压力浸渍(GVPI)工艺[1]的各类发电机或电动机定子绕组与线圈的考核也存在很大的困难。
业内对于考核单只定子线圈内部绝缘气隙放电的测试方法主要为三电极测试介质损耗因数,而更接近于真机运行状态的整机绕组绝缘内外气隙放电情况更加受到业内的关注。作为其中一项重要的考核手段,整机绕组两电极介质损耗因数测试却因受到绕组端部较大的电导性泄漏电流的干扰而无法准确表征绕组整体绝缘性能。
笔者对高压电机定子条式线棒的槽部与端部进行了绝缘结构和防晕结构分析。首次建立了线棒槽部与端部的两电极介质损耗因数及对地电容的电路模型。使用两电极测试方法分别测试并分析了电极长度与外施电压对整体性良好线棒与严重脱壳线棒的介质损耗因数与电容的影响,计算得到了介质损耗因数与电容的关系,为高压电机整机介质损耗因数的计算提供了理论支撑和试验依据。结果表明,绝缘整体性良好线棒的介质损耗因数与电容均由恒定的槽部初始值与线性增加的端部增量叠加而成。而绝缘严重脱壳线棒的介质损耗因数与电容则包括恒定的槽部分量、激增的槽部增量与线性增加的端部增量。
2 试验部分
2.1 试验样品
1) 3只额定线电压Un为13.8 kV的真机定子线棒(1号~3号),绝缘整体性良好。
2) 3只额定线电压Un为13.8 kV的真机定子线棒(4号~6号),经冷热循环处理后线棒主绝缘与铜线脱空,绝缘严重脱壳。
2.2 试验设备
LDSV-6型局放介质损耗测量仪。
2.3 测试方法
按照IEEE std 286中两电极方法测试。
2.4 试验线路
线棒介质损耗因数与电容的两电极测试线路如图1所示。
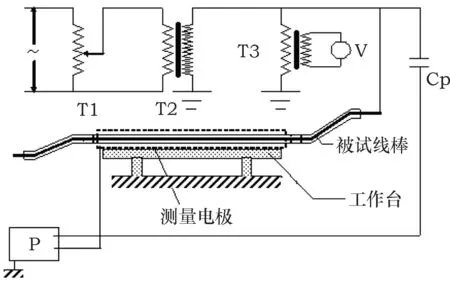
T1. 调压器; T2. 试验变压器; T3. 高压表; Cp. 标准电容器;
2.5 测试电极长度
线棒某一端的测试电极长度如图2所示,假设另一端结构相同且对称。测试电极长度由点P处向两端延伸,每次电极两端各延长20 mm,即测试电极长度分别等于每次铝箔包裹的长度L0、L1、L2、L3、L4、L5,相邻Li的增量ΔL均为40 mm,同时第一次铝箔包裹长度L0等于可见低阻长度。
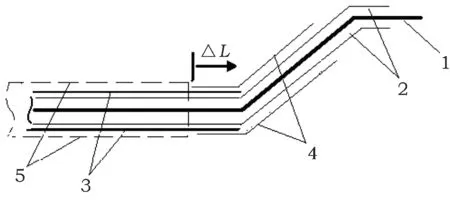
1. 线棒铜线; 2. 线棒主绝缘; 3. 线棒槽部低阻层;
2.6 试验电压
对线棒施加工频交流电压,测试电压为0~Un,其中tanδ0为线棒在气隙放电前的介质损耗因数初始值,Δtanδ为线棒气隙放电前后的介质损耗因数变化值,C0为线棒在气隙放电前的对地电容初始值,ΔC为线棒气隙放电前后的电容变化值。
2.7 试验结果
绝缘整体性良好的1号线棒的介质损耗因数tanδ与电容C随施加电压U的变化情况如图3~图4所示。
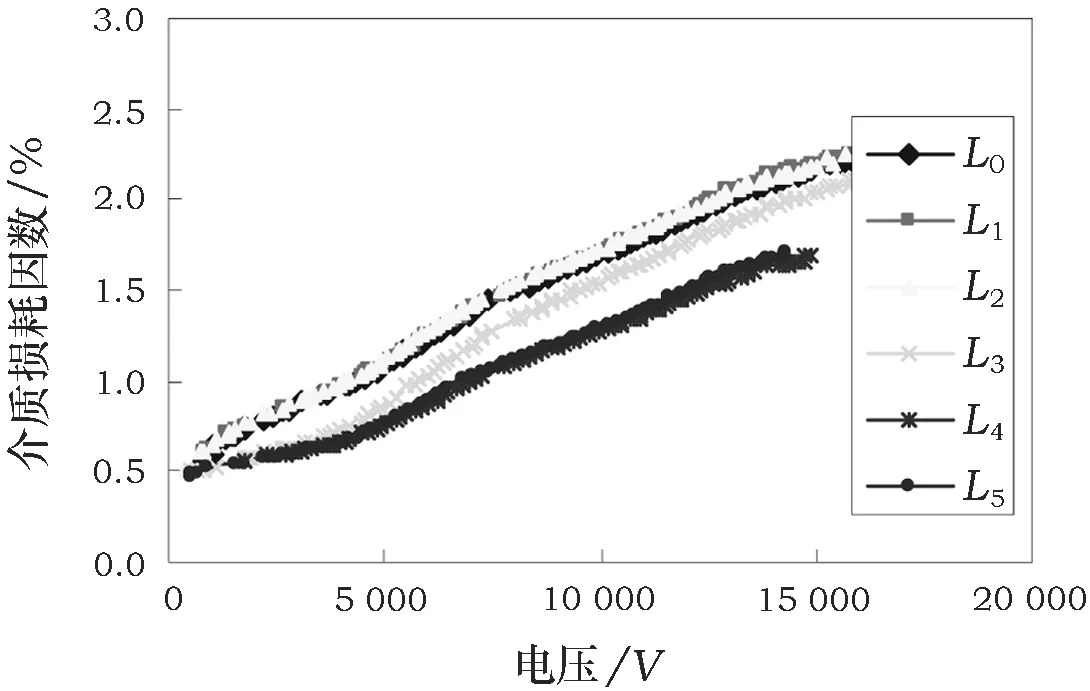
图3 1号线棒tanδ~U在不同电极长度下的曲线
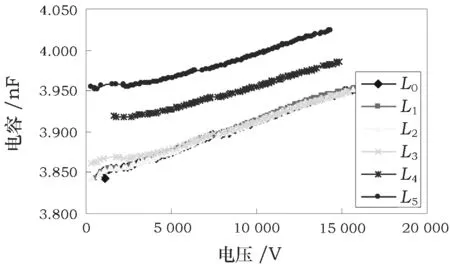
图4 1号线棒C~U在不同电极长度下的曲线
由图3和图4可知,无论电极长度如何变化,随着外施电压的升高,线棒的tanδ与C基本线性增加。同时前面4个电极长度(L0,L1,L2,L3)下的tanδ~U曲线与C~U曲线基本上分别重合;后面2个电极长度(L4,L5)下,tanδ减小而C增大。
绝缘严重脱壳的4号线棒的介质损耗因数tanδ与电容C随施加电压U的变化情况如图5~图6所示。
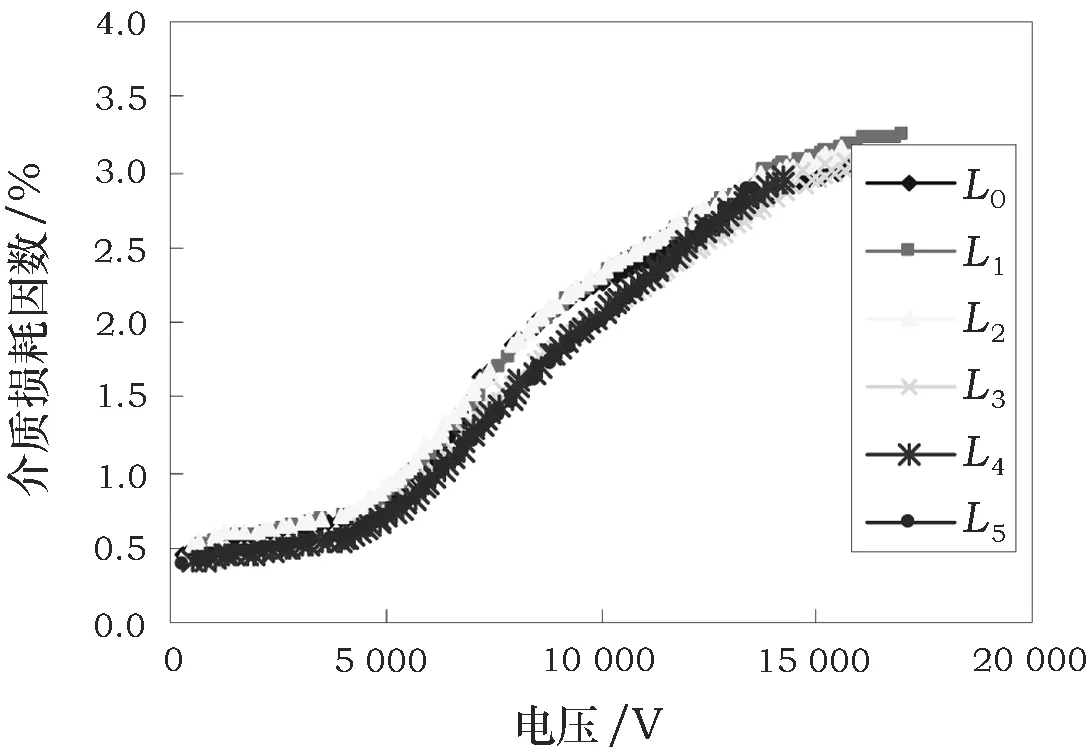
图5 4号线棒tanδ~U在不同电极长度下的曲线

图6 4号线棒C~U在不同电极长度下的曲线
由图5和图6可知,无论电极长度如何变化,随着外施电压的升高,线棒的tanδ与C均经历了基本不变至连续增长的过程。同时前面4个电极长度(L0,L1,L2,L3)下的tanδ~U曲线与C~U基本上分别重合;在后面2个电极长度(L4,L5)下,tanδ略微减小而C增大。
3 理论模型
3.1 线棒两电极介质损耗因数的构成
分析线棒绝缘结构、防晕结构和两电极测试线路可知:两电极介质损耗因数包括线棒槽部介质损耗因数与线棒端部介质损耗因数两部分。根据复合介质并联组合的等值计算公式[2]可知,线棒槽部和端部的合成介质损耗因数tanδ(即线棒介质损耗测试值)可用式(1)计算得到。该公式可用于叠加计算线棒介质损耗因数tanδ及其两个组成分量(槽部介质损耗tanδs与端部介质损耗tanδe)的数值关系,而不适用于分别计算槽部或端部介质损耗及其增量。
(1)
式中:tanδs为线棒槽部绝缘的介质损耗;tanδe为线棒端部绝缘的介质损耗;Cs为线棒槽部绝缘的电容;Ce为线棒端部绝缘的电容。
而线棒槽部或端部的介质损耗分别由线棒在较低电压下的初始介质损耗因数tanδ0及线棒在较高电压下的介质损耗增量Δtanδ组成,如式(2)所示。
(2)
MOHSEN.F[3]认为介质损耗主要来自四个方面:流经绝缘体内或表面的电导损耗、由偶极子转向极化引起的松弛损耗、空间电荷引起的界面极化损耗以及气隙击穿引起的局部放电损耗。
3.2 线棒两电极电容的构成
在忽略线棒端部杂散电容和寄生电容情况下,线棒两电极电容C主要包括线棒测试电极范围内的静态电容C0与外施高压作用下的等值电容增量C1两部分。等值电容增量C1只在外施高压达到一定数值时存在,包括槽部气隙放电增量ΔCs和端部电极效应引起的电容增量ΔCe。
3.3 介质损耗损耗因数初始值tanδ0
线棒介质损耗因数初始值包括槽部绝缘介质损耗初始值与端部绝缘介质损耗初始值。
3.3.1 槽部介质损耗初始值tanδs0
在施加电压较低且绝缘内部气隙的电压尚未达到气隙击穿所需的电压值时,线棒槽部介质损耗测试值,槽部绝缘介质损耗初始值表征了线棒自身绝缘特性,由线棒绝缘结构、绝缘工艺和绝缘材料所决定。主要由槽部绝缘内部的电导损耗和松弛损耗贡献。
3.3.2 端部介质损耗初始值tanδe0
在刚施加电压时,线棒端部介质损耗测试值。端部介质损耗初始值主要表征了线棒端部防晕特性,由端部防晕材料、防晕结构、防晕工艺所决定,主要由端部表面含SiC材料的防晕层的电导损耗贡献。
3.4 介质损耗因数增量Δtanδ
线棒介质损耗增量包括槽部绝缘介质损耗增量Δtanδs与端部介质损耗增量Δtanδe。
3.4.1 槽部绝缘介质损耗增量Δtanδs
槽部绝缘介质损耗增量主要由绝缘内部气隙击穿放电引起,主要由局部放电损耗所贡献。介质内部气隙放电击穿的模型[4]如图7所示。
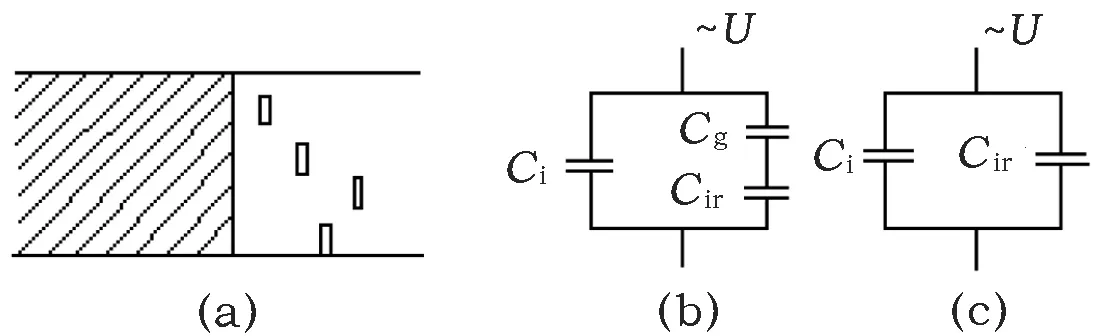
(a) 介质内部气隙放电模型,左侧为不放电部分,右侧为含有放电气隙的支路;(b) 放电前等值电路;(c) 放电后等值电路。图7 介质内气隙放电模型及等值电路
在图7中,Ci为与放电气隙处于不同支路的气隙和介质的总电容,Cg为放电气隙的总电容,Cir为与放电气隙位于同一条支路中的气隙和介质的总电容。
在气隙两端电压逐渐增加且在一定电压下发生击穿并形成导电通道时,相当于气隙短路,该支路电容增加。而不放电介质的等值电阻和等值电容均不发生变化。因此,随着外施电压的升高,槽部介质损耗增量Δtanδs只与槽部等值电容增量ΔCs有关。
3.4.2 端部介质损耗增量Δtanδe
因为线棒端部表面拥有可均匀端部表面电位分布的防晕层(以SiC为基材)且外施电压最高只有Un。所以线棒端部表面电位梯度远低于其四周空气氛围的表面放电所需的电场强度,不会引起线棒端部表面电晕或火花放电,进而增加线棒端部表面放电的附加损耗。因此,端部介质损耗增量主要由端部表面防晕层的电导损耗随外施电压的升高而增加引起的。定子线棒端部等值电路图如图8所示。
因为线棒端部表面防晕层的表面电阻阻抗远小于表面容抗,端部对地容抗远小于体积电阻阻抗,所以图8(a)可简化为图8(b)[5]。
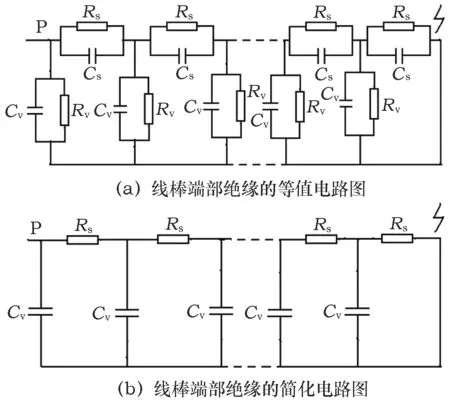
Cs. 单位长度的表面电容,Cv. 单位体积的体积电容,Rs. 单位长度的表面电阻,Rv. 单位体积的体积电阻图8 定子线棒端部等值电路图
因此,端部介质损耗增量可以认为是由单位长度表面电阻与对应的单位体积的体积电容两者组成的电路单元在外施电压下的数值变化引起的。在单位体积电容随外施电压基本不变的条件下,端部介质损耗增量Δtanδe只与单位长度表面电阻的连续降低(即防晕层的电阻非线性)有关。
很多研究指出[5-7],当SiC防晕材料外施场强E不高于4 kV/cm时,材料表面电阻率的对数lgρ与外施场强E的关系近似于负线性关系。而端部介质损耗正比于端部有功电流,即反比于端部表面电阻率。因此,可以认为Δtanδe∝1/lgρ。宋建成等[5]指出,在外施场强变化范围较小时,对数曲线lgρ~E与曲线ρ~E差异很小。因此,随着外施电压的升高,端部介质损耗也随之线性增加。
同时随着外施电压的升高,与点P相邻的第一个电路单元中表面电阻逐渐降低以至于对应的对地电容被短路,相当于介质损耗或电容测试电极延长,引起电极等值电容的增加。后续电路单元也将依次出现类似现象。
值得注意的是,当外施电压继续升高时,线棒端部泄漏电流或端部介质损耗因数将呈现出非线性增长的趋势。
3.5 槽部介质损耗及其增量与电容及其增量的数值关系(局部放电类型)
在交变电场下介质的介质损耗因数tanδ如式(3)所示[8]。
(3)
式中:时间常数τ为电阻R和电容C的乘积。
该公式表征了绝缘介质损耗因数与电容随外施电压变化的关系,可用于计算槽部介质损耗和电容在绝缘内部气隙击穿放电前后的数值变化,适用于局部放电损耗计算。
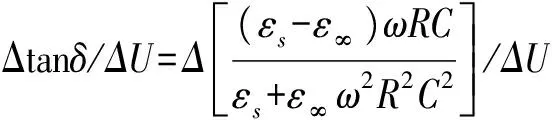
(4)
考虑到室温下工频电压(ετ≪1)和环氧云母介质的极化主要由偶极子转向极化构成的条件(εs>ε∞)[9],式(4)可简化为式(5)。
Δtanδs≈tanδs0·ΔCs/C0
(5)
对于线棒槽部绝缘来说,如果放电前的电容C0和介质损耗因数tanδs0为定值,则放电前后的介质损耗因数增量Δtanδs与电容变化量ΔCs成正比。
3.6 线棒介质损耗和电容计算公式
3.6.1 绝缘整体性良好线棒
绝缘整体性良好的线棒意味着线棒槽部绝缘的介质损耗因数和电容基本不随外施电压升高而变化,可以认为定值,即Δtanδs和ΔCs为0。因此,线棒两电极介质损耗tanδ和电容C可由式(6)和式(7)表述。
(6)
C=C0+C1=C0+ΔCe
(7)
在式(6)中,等号右侧的第1部分基本不随电压变化,等于线棒刚施加电压时的介质损耗测试值;等号右侧的第2部分为电压的变量,它引起线棒介质损耗测试值的变化。
在式(7)中,等号右侧的第1部分C0基本不随电压变化,为线棒刚施加电压时的电容测试值;等号右侧的第2部分为电压的变量,它引起线棒电容测试值的变化。
3.6.2 绝缘严重脱壳线棒
绝缘严重脱壳的线棒意味着线棒槽部绝缘的介质损耗因数和电容随外施电压升高而增大,均为电压的函数。因此,线棒两电极介质损耗tanδ和电容C可由式(8)和式(9)表述。
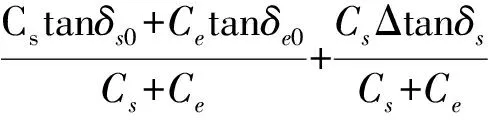
(8)
C=C0+C1=C0+ΔCs+ΔCe
(9)
在式(8)中,等号右侧第1部分基本不随电压变化,为线棒刚施加电压时的介质损耗测试值;等号右侧第2部分和第3部分为电压的变量,引起线棒介质损耗测试值的变化。
在式(9)中,等号右侧第1部分基本不随电压变化,为线棒刚施加电压时的电容测试值;等号右侧的第2部分和第3部分为电压的变量,引起线棒电容测试值的变化。
3.7 线棒介质损耗和电容中各分量典型曲线
3.7.1 绝缘整体性良好线棒
绝缘整体性良好线棒的tanδ~U的典型曲线或C~U典型曲线如图9所示。
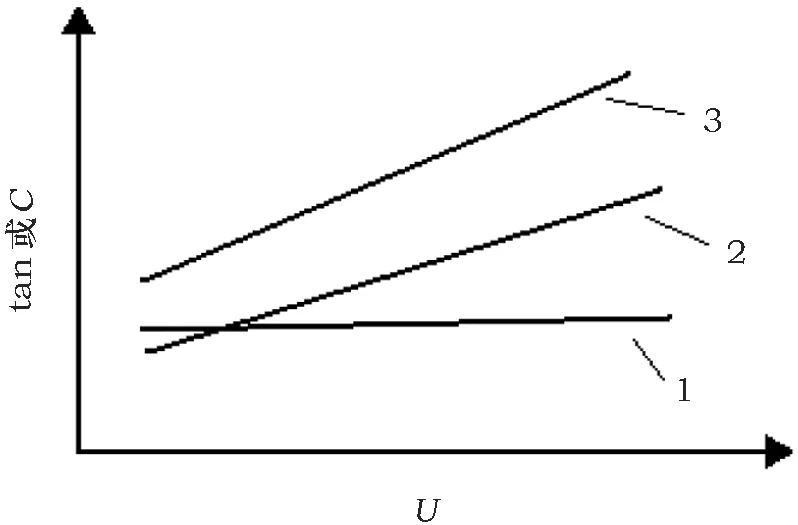
1. tanδs; 2. tanδe; 3. tanδ图9 绝缘整体性良好线棒的典型曲线
3.7.2 绝缘严重脱壳线棒
绝缘严重脱壳线棒的tanδ~U的典型曲线或C~U典型曲线如图10所示。
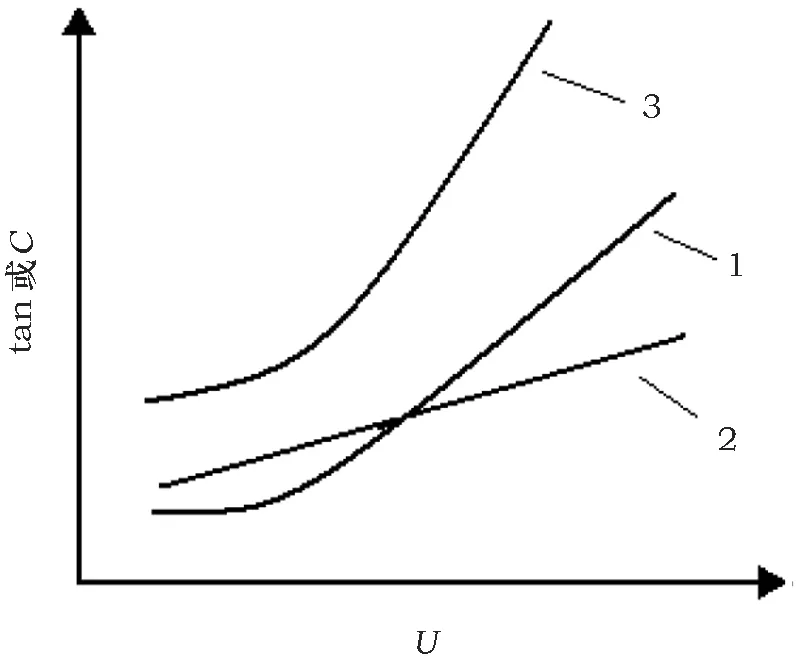
1. tanδs; 2. tanδe; 3. tanδ图10 绝缘严重脱壳线棒的典型曲线
4 结果与分析
4.1 电极长度对整体性良好线棒的影响
4.1.1 介质损耗因数tanδ
由图11可知,1号线棒电极长度从L0开始(令ΔL=0),随着电极长度的增加,不同电压下的曲线趋势基本一致,均为先基本不变再减小。曲线拐点对应的电极长度为图2中项3的低电阻防晕带长度。
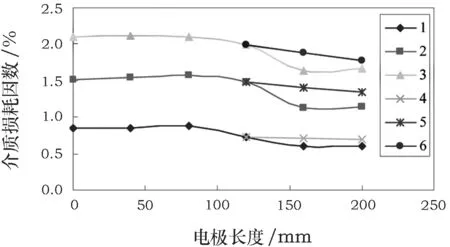
1. 0.2Un下实测值; 2. 0.6Un下实测值; 3. 1.0Un下实测值;
假设线棒槽部与端部的截面尺寸相同且介质均匀,则槽部与端部的电容之比即等于长度之比。根据ΔL=120 mm的介质损耗测试值,可由式(6)计算得到后续计算值,如图11所示。值得注意的是,因为端部绝缘介质损耗计算条件取值存在较大的不确定性,所以介质损耗计算值和实测值也存在较大的差异。
4.1.2 电容C
由图12可知,1号线棒电极长度从L0开始(令ΔL=0),随着电极长度的增加,不同电压下的曲线趋势基本一致,均为先基本不变再增大。曲线拐点对应的电极长度为图2中项3的低电阻防晕带长度。
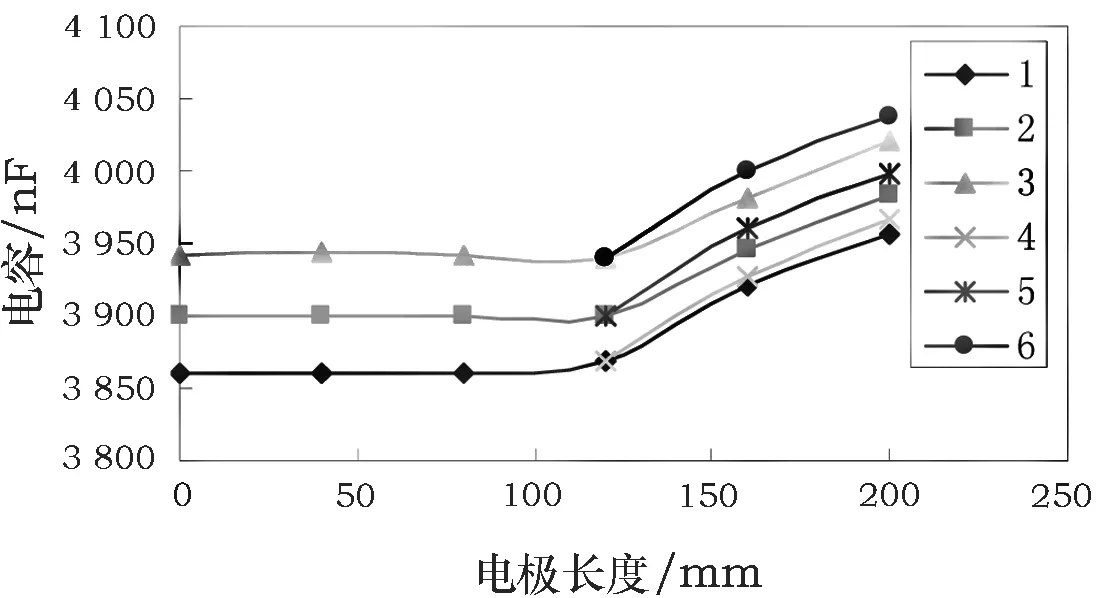
1. 0.2Un下实测值; 2. 0.6Un下实测值; 3. 1.0Un下实测值;
假设线棒槽部与端部的截面尺寸相同且介质均匀,则电容的增加即等于长度的增加。根据ΔL=120 mm的电容测试值,可由式(7)计算得到后续计算值,如图12所示。测试曲线与计算曲线具有较好的一致性。
4.2 电极长度对绝缘脱壳线棒的影响
4.2.1 介质损耗因数tanδ
由图13可知,4号线棒电极长度从L0开始(令ΔL=0),随着电极长度的增加,不同电压下的曲线趋势基本一致,均为先基本不变再略微减小。曲线拐点对应的电极长度为图2中项3的低电阻防晕带长度。
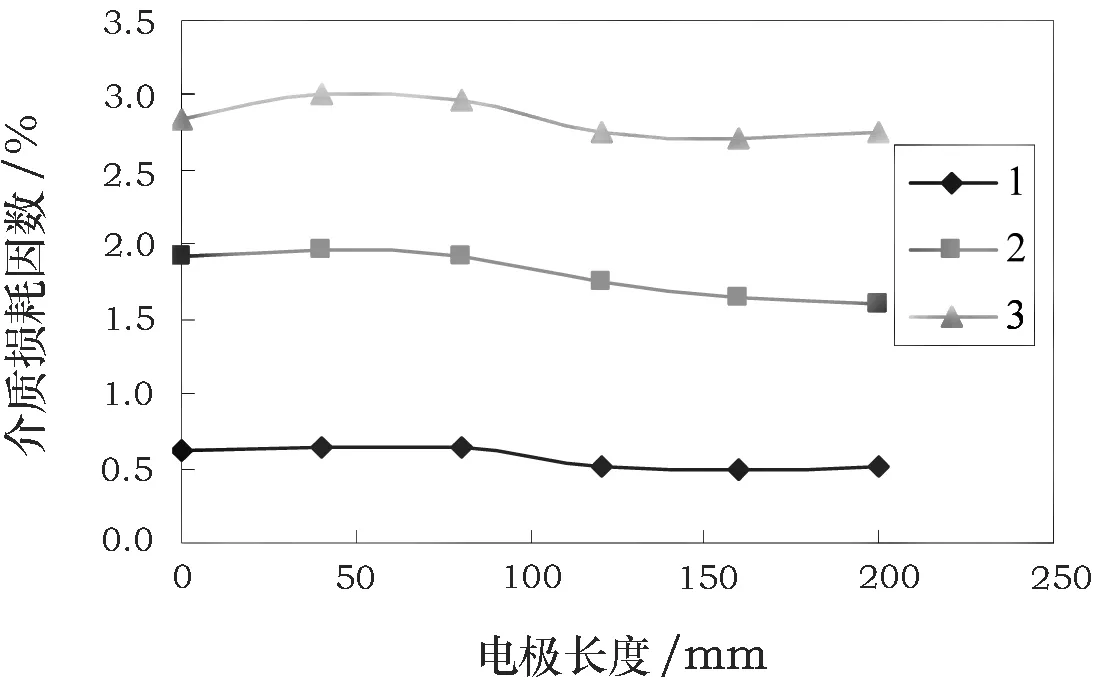
1. 0.2Un实测值;2. 0.6Un实测值;3. 1.0Un实测值
在图5和图13中,电极长度(或各部分电容)对tanδ的影响并不明显,这是因为Δtanδs远大于Δtanδe且Cs大于Ce而使式(8)中等号右侧第3部分为第2部分所掩盖。
4.2.2 电容C
由图14可知,4号线棒电极长度从L0开始(令ΔL=0),随着电极长度的增加,不同电压下的曲线趋势基本一致,均为先基本不变再增大。曲线拐点对应的电极长度为图2中项3的低电阻防晕带长度。
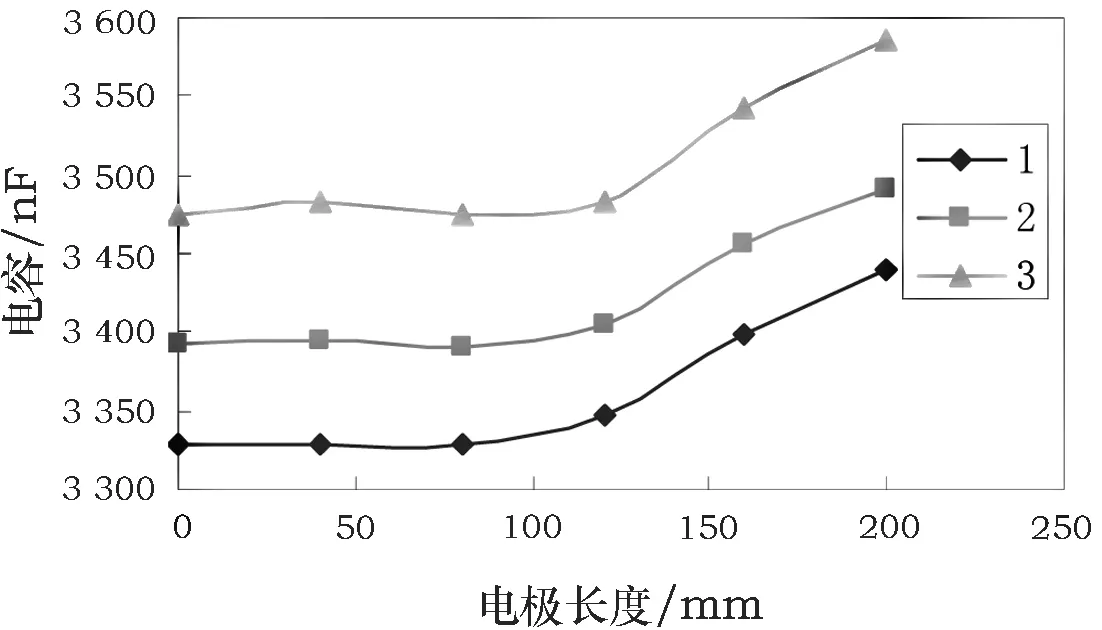
1. 0.2Un实测值; 2. 0.6Un实测值; 3. 1.0Un实测值
4.3 电极长度对曲线计算的意义
由图3~图6中不同电极长度下各曲线互相平行或重合可知:在相同电压下,在线棒电极长度两端各延长0~100 mm范围内,线棒端部未被电极覆盖的部分的Δtanδe~U曲线和ΔCe~U曲线特性未发生变化,只是槽部与端部各自所占电容比例发生了变化。
由图11~图14中不同电压下各曲线互相平行可知:在相同电极长度下,线棒端部的Δtanδe数值和ΔCe数值与外施电压U近似于线性增加,因此在实际计算中Δtanδe~U曲线和ΔCe~U曲线可简化为线性关系。
4.4 绝缘脱壳线棒的tanδ~U曲线计算
假设相同形状和结构的不同线棒端部防晕系统相同时,tanδe~U特性也基本相等,则可以通过测试相同形状和结构的2号和3号线棒的tanδ~U曲线并分解出tanδe~U曲线。
根据4号线棒C~U曲线并按照式(5)和式(8)可计算得到4号线棒tanδ~U曲线,如图15所示。
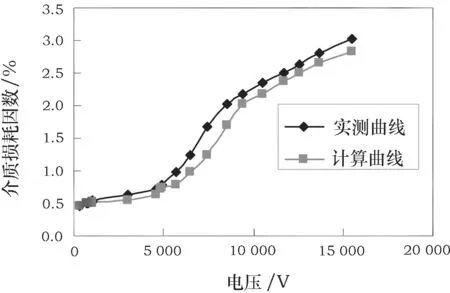
图15 4号线棒tanδ~U实测曲线与计算曲线
由图15可知,实测曲线与计算曲线基本一致,这说明:对于绝缘脱壳线棒来说,Δtanδs远大于Δtanδe且Cs大于Ce,同时相关计算比较符合式(5)。
5 结语
1) 首次建立了高压电机定子线棒两电极介质损耗因数和电容的等值电路模型。
2) 首次建立了高压电机定子线棒两电极介质损耗因数和电容的各组成分量的数值计算模型。
3) 绝缘整体性良好线棒的介质损耗因数与电容均由恒定的槽部初始值与线性增加的端部增量叠加而成。
4) 绝缘严重脱壳线棒的介质损耗因数与电容包括恒定的槽部组分、激增的槽部增量与线性增加的端部增量。
[1] 顾家华.电机绕组真空连续浸渍绝缘工艺简析[J].微特电机,2005,30(5):35~38.
[2] 夏英来.大型发电机定子槽内振动火花放电机理[J].高电压技术,2013,39(4):1009~1017.
[3] 何景彦,吴广宁,高波.基于介质损耗分析研究变频电机绝缘老化特性[J].高压电器, 2008,44(3):243~245.
[4] 胡波,梁智明,皮如贵. 大型水轮发电机定子线棒气隙群放电的特性研究[J].绝缘材料, 2009,42(1):39~43.
[5] 宋建成,乐波,谢恒堃. 大电机主绝缘多因子老化试验中试样线棒端部防晕技术的研究[J]. 电工技术学报. 2000, 15(3):1~5.
[6] 谢磊,宁叔帆,于开坤. 碳化硅非线性导电特性的研究进展[J]. 绝缘材料。2005.(3):60~65.
[7] 于开坤,宁叔帆,赵丽华. 防晕层厚度和碳化硅含量对其电学性能影响因素的研究[J]. 绝缘材料. 2005,(3):29~34.
[8] 金维芳.电介质物理[M].北京:机械工业出版社,1995.70~75.
[9] 胡波,谢志辉,何明鹏. 电机定子线棒绝缘介质损耗特性研究[J].防爆电机, 2012,47(2):25~28.
胡波,男,1981年生,硕士研究生,工程师,毕业于西安交通大学电气绝缘专业,现从事高压电机绝缘工艺研究。
·信息点滴·
菲律宾仍有516万kW水电资源待开发
据《菲律宾星报》2014年8月22日报道,菲能源部的数据显示,菲未开发的水电资源在516万kW左右,其中吕宋地区待开发的有358万kW,棉兰老岛有86万kW,米沙鄢地区有72万kW,共需约130亿美元的投资。菲律宾目前水电总装机容量为349万kW,占全国总装机容量的13.7%,水电装机容量落后于越南、泰国和印尼。
20140403

