新阈值二进小波去噪算法在齿轮信号中的应用

苏成志，陈洪印，孟凡一，王德民，于培章

长春理工大学机电工程学院，长春 130022

新阈值二进小波去噪算法在齿轮信号中的应用

苏成志，陈洪印，孟凡一，王德民，于培章

长春理工大学机电工程学院，长春 130022

1 引言

随着激光技术的不断发展，齿轮的激光检测必将成为今后齿轮检测的一个发展方向。在齿轮信号的采集过程中，不可避免地会受到外界干扰光、齿轮表面粗糙度、激光入射角度、外界振源等因素的影响，从而在采集信号中引入噪声，导致采集信号不能准确地反映被测齿轮的特征信息，影响了齿轮检测的准确性。所以，在分析和计算齿轮误差参数之前，首先需要对原始采集信号进行去噪处理，提取出纯净的齿轮信号。

针对激光检测的原始齿轮信号，由于干扰因素的不确定性和复杂性，传统软、硬阈值函数去噪的效果很不理想。因此，本文在分析传统软、硬阈值函数去噪方法的基础上，提出一种可调的新阈值函数去噪方法，该方法改善了传统软、硬阈值函数去噪中的不足。由于信号在二进小波变换域内，其表达具有冗余性，在相同的误判概率下，基于二进小波变换的去噪效果要好于离散小波变换的信号去噪[1]，因此，本文采用了二进小波变换代替传统的离散小波变换。经仿真实验验证，本文提出的去噪方法不仅能提高信噪比和适用性，并且能够克服伪吉布斯现象对重构信号的影响，适用于齿轮检测信号的去噪处理。

2 原始齿轮信号的采集

将某渐开线直齿内齿轮水平放置于测量平台上，由转台带动激光测量头在内齿轮内作水平面的旋转扫描，其检测条件为：激光位移传感器的采样频率为5 000 Hz、转台的转速为1 r/min、采样点数为10万，原始齿轮信号如图1所示。

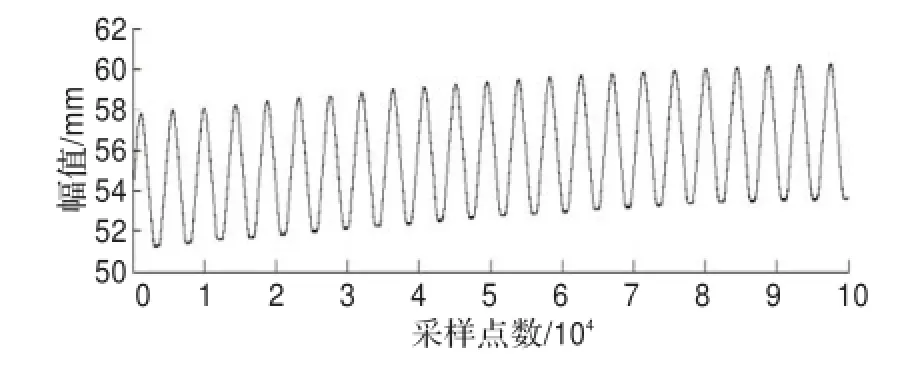
图1 原始齿轮信号

3 新阈值函数的确定

在小波去噪过程中，门限阈值将直接影响着小波去噪的效果[2-7]，因此，阈值函数及阈值λ的确定是一个关键性问题。传统的阈值函数有两种[8]：传统硬值函数和软阈值函数，其中，传统硬阈值函数如式（1）所示：该方法获得的重构信号具有较好的逼近性，但由于阈值函数本身不连续，很容易导致重构信号出现附加振荡[9]。所以，该方法在齿轮信号的重构过程中，容易改变齿轮的特征点信息，从而影响齿轮检测的后续分析。传统软阈值函数如式（2）所示：

该方法获得的重构信号具有较好的光滑性，但由于小波系数的绝对值大于某一阈值时，小波系数的估计值与分解的小波系数之间以较高的概率存在着恒定的偏差，导致误差相对较大[10]。所以，该方法在齿轮信号的重构过程中，容易改变齿轮的齿面粗糙度的真实值，不能满足高精度的齿轮检测要求。

鉴于传统软、硬阈值函数在齿轮信号的去噪过程中都存在严重的缺陷，本文根据传统软、硬阈值函数折中的思想，提出了一种可调的新阈值函数，如式（3）所示：

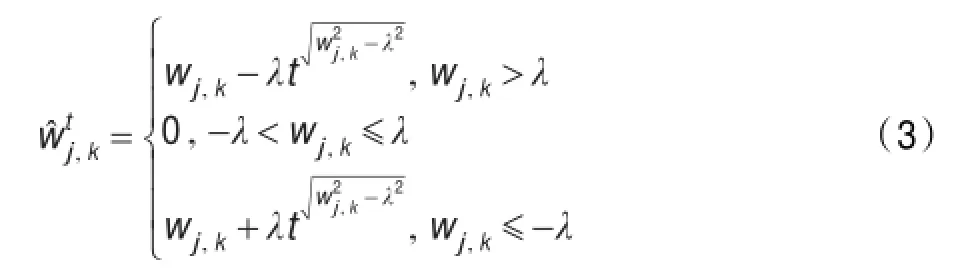
式（3）中，λ是阈值，t是调节因子，0≤t≤1。

当t越大，新阈值函数越接近于传统软阈值函数，当t越小，新阈值函数越接近于传统硬阈值函数。新阈值函数随调节因子t的变化关系如图2所示，图中虚线表示硬阈值函数，点划线表示软阈值函数，实线表示新阈值函数。在新的阈值函数中，是一个动态调整阈值，其中，，且是一个减函数。当wj.k=λ时，动态阈值为λ。当||wj，k＞λ时，随着wj，k的不断增加，呈指数形式不断减小。所以，当||wj，k＞λ时，随着wj.k的不断增加，动态调整阈值呈指数形式不断减小，解决了传统软阈值函数中存在恒定偏差而导致相对误差较大的问题，同时也解决了传统硬阈值函数的不连续而导致重构信号出现附加振荡的问题。该方法在齿轮信号的去噪过程中，不仅不会改变齿轮信号的特征点信息，而且对齿面粗糙度的影响很小。所以，该方法适用于齿轮检测信号的去噪处理。

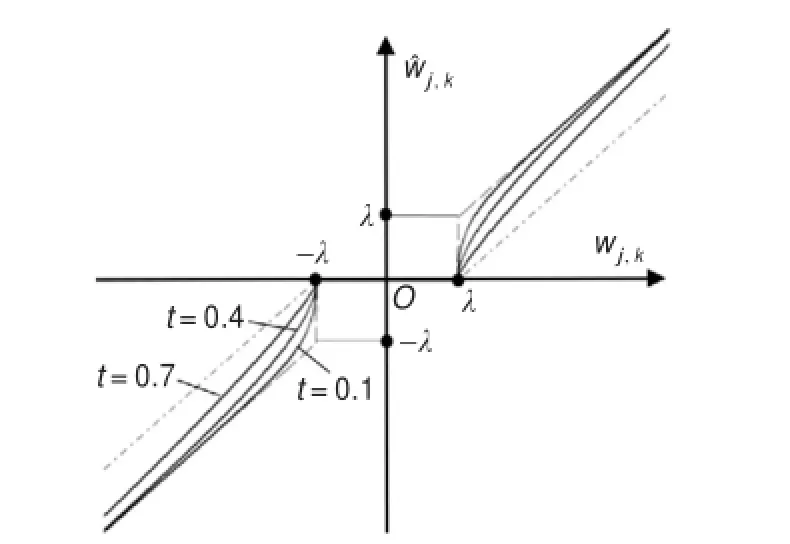
图2 阈值函数对比图

4 阈值λ的确定

通常噪声的幅值低于σ2lgN的概率非常高[11-12]，所以可取通用阈值为：

式（4）中，N为信号长度，σ为噪声信号标准差，可通过最小尺度上的小波系数来估计，其估计值为：

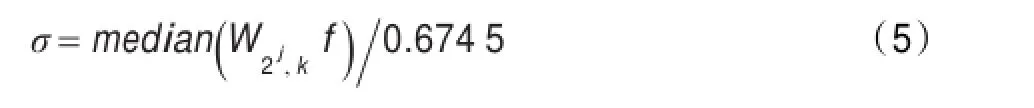
基于噪声的小波系数幅值随分解尺度的增加而减小的特性，使各尺度阈值随尺度的变化而变化[13-14]，可确定各尺度的阈值λj为：

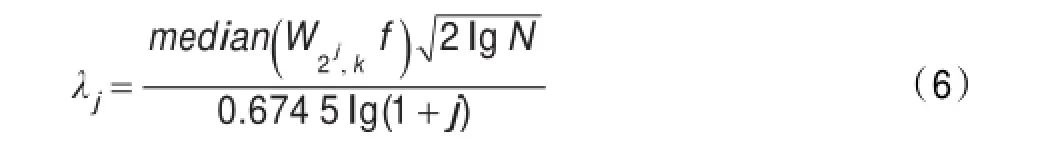
式（6）中，j为二进小波分解尺度。

5 新阈值函数去噪的对比验证

为了验证新阈值函数的可行性，在Matlab中利用wnoise函数产生典型的blocks、bumps、heavy sine及doppler四个信号作为仿真实验对象，它们的信噪比分别为18.647 5 dB、16.94 8 dB、16.097 3 dB和15.166 6 dB，采样点数均为1 024。在仿真实验中，传统软、硬阈值函数法、新阈值函数法均采用sym6小波，并进行5层的小波分解，新阈值函数的调节因子t取0.12，t的选取是以bumps函数为仿真实验对象，经过多次实验，发现t取0.12时，去噪效果较好。基于二进小波变换的传统软、硬阈值函数法、新阈值函数法均进行5层的二进小波分解。为了比较不同处理方法的降噪效果，引入信噪比（SNR），均方根误差（RMSE）作为评价标准[15]，定义如下：

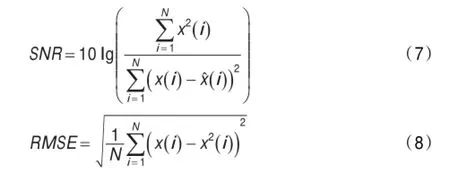
仿真实验结果如表1及图3所示。由表1可知，新阈值函数法与传统软、硬阈值函数法相比，SNR平均值分别提高了1.905 7 dB和2.794 4 dB，RMSE平均值分别减小了0.215 1和0.314 6。基于二进小波变换的新阈值函数法与基于二进小波变换的传统软、硬阈值函数法相比，SNR平均值分别提高了1.836 6 dB和0.611 4 dB，RMSE平均值分别减小了0.091和0.033 2。说明了本文提出的新阈值函数明显优于传统软、硬阈值函数。基于二进小波变换的新阈值函数法与新阈值函数法相比，SNR平均值提高了5.463 1 dB，RMSE平均值减小了0.145 9。说明了二进小波变换的去噪效果明显优于离散小波的去噪效果。

由图3可知，基于二进小波变换的新阈值函数去噪算法的去噪效果明显优于传统软、硬阈值函数法的去噪效果，特别是在信号的特征部分，本文提出的去噪算法能够有效地克服伪吉布斯现象对信号的影响。

6 新阈值二进小波去噪算法的齿轮原始信号去噪

对齿轮原始信号进行5层的二进小波分解，然后采用新阈值法对各层高频二进小波系数作阈值量化处理，最后对低频二进小波系数和阈值处理后的高频二进小波系数进行重构，重构信号如图4所示。由图4可知，经新阈值二进小波去噪算法处理后的齿轮信号明显地消除了噪声，齿轮信号的特征点信息弱化问题得到了明显的改善，有利于齿轮检测的后续数据分析。

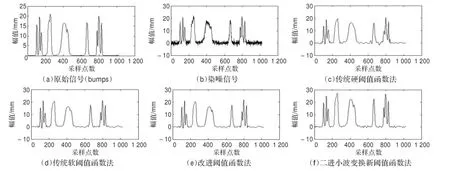
图3 不同去噪方法处理的结果对比

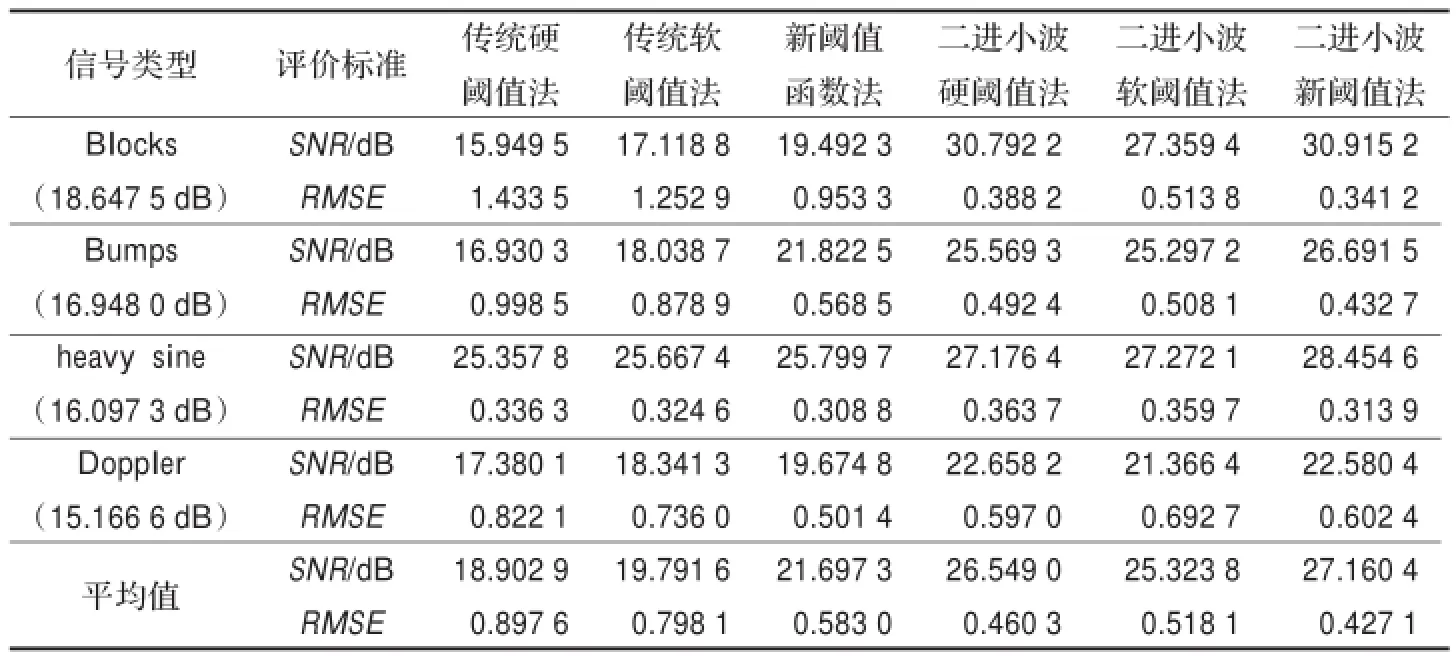
表1 不同去噪方法处理的去噪结果

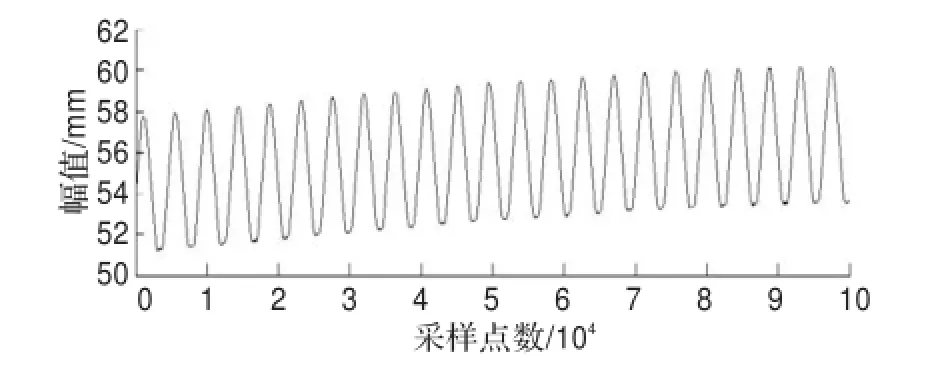
图4 齿轮重构信号

7 结束语

本文在分析传统软、硬阈值函数的不足的基础之上，提出了一种新阈值二进小波去噪算法，该方法改进了传统软、硬阈值函数法在齿轮信号去噪过程中的不足。经实验验证，该算法的信噪比和适用性均有明显的改善，而且能够降低伪吉布斯现象对重构信号的影响，适用于齿轮检测原始信号的去噪处理，为齿轮检测的后续数据分析提供了良好的数据基础，因而在齿轮检测过程中具有十分重要的价值。

[1]刘杰，朱启兵，李允公，等.基于新阈值函数的二进小波变换信号去噪研究[J].东北大学学报：自然科学版，2006，27（5）：536-539.

[2]蒋克荣，唐向清，朱德泉.基于改进阈值小波算法的汽车轮速信号处理[J].仪器仪表学报，2010，31（4）：736-740.

[3]林杰，付梦印，李道平.自适应小波阈值去噪算法及在图像处理中的应用[J].兵工学报，2011，32（7）：896-900.

[4]张通，张骏，张怡.基于改进小波阈值的激光陀螺漂移信号降噪[J].仪器仪表学报，2011，32（2）：258-263.

[5]Khare A，Tiwary U S，Pedryca W，et al.Multilevel adaptive thresholding and shrinkage technique for denoising using Daubechies complex wavelet transform[J].Imaging Science Journal，2010，2：340-358.

[6]Zang Huaigang，Wang Zhibin，Zheng Ying.Analysis of signal de-noising method based on an improved wavelet thresholding[C]//The 9th International Conference on Electronic Measurement and Instruments，2009，4：987-990.

[7]Om H，Biswas M.An improved image denoising method based on wavelet thresholding[J].Journal of Signal and Information Processing，2012，3：109-116.

[8]Donoho D L.De-noising by soft-thresholding[J].IEEE Trans on Inform Theory，1995，41（3）：613-627.

[9]惠飞，史昕，赵祥模，等.基于改进阈值函数的小波去噪算法研究[J].现代电子技术，2011，34（12）：61-68.

[10]张茁生，任品毅.自适应二进小波去噪法[J].工程数学学报，2009，26（6）：969-976.

[11]张宗平，刘桂忠，董恩清.基于二进小波变换的信号去噪[J].电子与信息学报，2001，23（11）：1083-1090.

[12]姜长泓，王龙山，尤文，等.基于平移不变小波的声发射信号去噪研究[J].仪器仪表学报，2006，27（6）：607-610.

[13]苑津莎，张冬雪，李中.基于改进阈值法的小波去噪算法研究[J].华北电力大学学报，2010，37（5）：92-97.

[14]李海东，李青.基于阈值法的小波去噪算法研究[J].计算机技术与发展，2009，19（7）：56-58.

[15]谢琦，陈维义，林伟.平移不变小波变换在消除电路噪声中的应用[J].舰船科学技术，2011，33（5）：74-77.

SU Chengzhi,CHEN Hongyin,MENG Fanyi,WANG Demin,YU Peizhang

College of Mechanical&Electric Engineering,Changchun University of Science&Technology,Changchun 130022,China

In the process of gear laser detection,due to the influence of various noise sources,the phenomenon of the original signal weakening of feature information will appear,which impacts the accurateness of gear detection.To solve this problem,a new de-noising method of combining a new threshold function and dyadic wavelet transform is proposed based on the analysis of the traditional soft and hard threshold function.In this method,adjustable threshold function is built.The threshold adjusts dynamically in the form of index,with the change of binary wavelet coefficients,overcoming the discontinuity of the hard threshold and the offset of the soft threshold.By simulation experiments,the signal to noise ratio and applicability of the method have significantly improved.

gear;dyadic wavelet transform;new threshold function;dynamic threshold;signal reconstruction

在齿轮的激光检测过程中，由于各种噪声源的影响，原始信号会出现特征信息弱化的现象，影响了齿轮检测的准确性。为解决该问题，在分析传统软、硬阈值函数不足的基础上，提出了一种新阈值函数和二进小波变换相结合的去噪方法。在该方法中构建了一个可以调节的新阈值函数，该阈值随二进小波分解系数的变化以指数形式动态调整，克服了传统硬阈值函数不连续和传统软阈值函数存在偏差的问题。经仿真实验验证，该方法的信噪比和适用性具有明显的改善。

齿轮；二进小波变换；新阈值函数；动态阈值；信号重构

A

TN911.72

10.3778/j.issn.1002-8331.1210-0138

SU Chengzhi,CHEN Hongyin,MENG Fanyi,et al.Application of new threshold dyadic wavelet de-noising algorithm on gear signal.Computer Engineering and Applications,2014,50（18）：206-209.

吉林省科技支撑计划项目（No.20110313）。

苏成志（1977—），男，博士研究生，副教授，主要从事光机电一体化检测方面的研究；陈洪印（1986—），男，在读硕士研究生，研究方向为精密、超精密加工、检测及装备；孟凡一（1985—），男，在读硕士研究生，研究方向为精密、超精密加工、检测及装备；王德民（1961—），男，副教授，主要从事机电系统控制与技术方面的研究。E-mail：chen_hongyin@126.com

2012-10-15

2012-12-25

1002-8331（2014）18-0206-04

CNKI网络优先出版：2013-03-13,http://www.cnki.net/kcms/detail/11.2127.TP.20130313.0946.001.html