拉普拉斯混合分布语音模型研究

侯玉宝，王景芳

湖南涉外经济学院信息科学与工程学院，长沙 410205

拉普拉斯混合分布语音模型研究

侯玉宝，王景芳

湖南涉外经济学院信息科学与工程学院，长沙 410205

1 引言

语音信号处理[1-2]以语音为研究对象，涉及心理学、生理学、语言学、人工智能和模式识别等多项研究领域，甚至还涉及到说话时的表情、手势等人的体态语言信息。由于语音是人们在日常生活中的主要交流手段，因此语音信号处理在现代信息社会中占有重要地位。近年来，随着语音信号处理技术的日益成熟，出现了新的基于语音识别的应用方向，如语音拨号、呼叫中心、移动设备中的嵌入式命令控制、发音学习以及基于关键词检出的口语会话系统等。随着语音信号处理技术在实际生活中的应用在不断发展，语音信号处理技术已经被广泛地接受和使用。由于语音比其他形式的交互方式具有更多的优势，因此这项技术已经越来越贴近人们的生活。目前，语音信号处理技术处于蓬勃发展时期，不断有新的产品被研制开发，市场需求逐渐增加，具有良好的应用前景。

语音研究离不开其分布模型[3-9]，以往大多假设在正态分布基础上；中心极限定理从理论上阐述了产生正态分布的条件，中心极限定理简单直观的阐述是：如果决定某一随机变量结果的是大量微小的、独立的随机因素之和，并且每一随机因素的单独作用相对均匀得小，没有一种因素可起到压倒一切的主导作用，那么这个随机变量一般近似服从于正态分布。正态分布广泛存在于自然现象、社会现象、科学技术以及生产活动中，在实际中遇到的许多随机现象都服从或者近似服从正态分布。但事实上语音是具有重尾特性的非平稳过程。Laplace分布具有峰度为6的重尾特性，本文研究Laplace分布语音模型与混合Laplace分布语音模型，并将两者语音模型进行对比分析。

2 语音的Laplace分布模型参数估计

2.1 重尾与峰度

相对于正态分布而言，以四阶中心矩为基础。四阶中心矩具有峰度（kurtosis）的含义，峰度是统计中描述分布状态的一个重要特征值，用以判断概率密度函数曲线相比于正态分布的尖平程度。如果将正态分布视为常峰态，密度函数曲线的形状比正态分布更高更瘦的称为高峰态，否则称为低峰态。正态分布的峰度为3。Laplace分布的峰度为6。正态云分布峰度在3～9之间[10]。

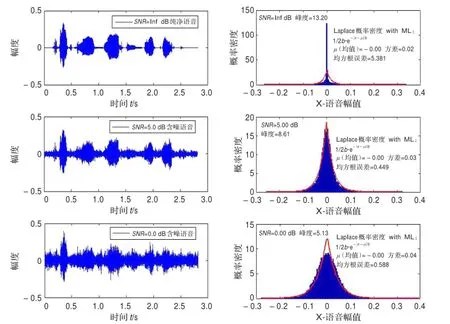
图1 正态云分布仿真结果

定义[7]随机变量X称为是重尾[11]的，如果峰度：

其中μ，σ分别为X的期望和标准差。

2.2 模型参数估计

2.3 实例验证与分析

取AURORA语音库[12]纯净语音“The birch canoe slid on the smooth planks.”文件sp01.wav，背景噪声选自Noisex-92数据库[13]。用纯语音、含babble噪声信噪比SNR=5、0 dB语音的正态云分布仿真结果如图1。图上RMS为平均误差，直方图等分区间200个。

3 混合Laplace分布语音模型

Laplace分布随机变量X的峰度为：K(X)=6，单个Laplace分布应用范围受限制。有必要研究混合Laplace模型使其适用于超重尾信号，如一般的纯语音峰度大都大于9。

3.1 EM算法原理

EM算法是Dempster，Laind，Rubin[14-15]于1977年提出的求参数极大似然估计的一种方法，它可以从非完整数据集中对参数进行MLE估计，是一种非常简单实用的学习算法。这种方法可以广泛地应用于处理缺损数据，截尾数据，带有噪声等所谓的不完全数据（incomplete data）。

假定集合Z=(X，Y)由观测数据X和未观测数据Y组成，Z=(X，Y)和X分别称为不完整数据和完整数据。假设Z的联合概率密度被参数化地定义为P(X，Y|Θ)，其中Θ表示要被估计的参数。Θ的最大似然估计是求不完整数据的对数似然函数L(X;Θ)的最大值而得到的：

EM算法包括两个步骤：由E步和M步组成，它是通过迭代地最大化完整数据的对数似然函数Lc(X;Θ)的期望来最大化不完整数据的对数似然函数，其中：

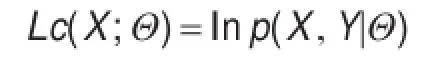
假设在算法第t次迭代后Θ获得的估计记为Θ(t)，则在(t+1)次迭代时，

E-步为计算完整数据的对数似然函数的期望，记为：

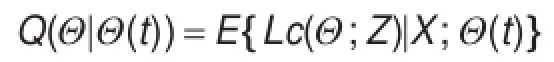
M-步为通过最大化Q(Θ|Θ(t))来获得新的Θ。

通过交替使用这两个步骤，EM算法逐步改进模型的参数，使参数和训练样本的似然概率逐渐增大，最后终止于一个极大点。直观地理解EM算法，它也可被看作为一个逐次逼近算法：事先并不知道模型的参数，可以随机选择一套参数或者事先粗略地给定某个初始参数λ0，确定出对应于这组参数的最可能的状态，计算每个训练样本的可能结果的概率，在当前的状态下再由样本对参数修正，重新估计参数λ，并在新的参数下重新确定模型的状态，这样，通过多次的迭代，循环直至某个收敛条件满足为止，就可以使得模型的参数逐渐逼近真实参数。

EM算法的主要目的是提供一个简单的迭代算法计算后验密度函数，它的最大优点是简单和稳定。

3.2 混合Laplace模型设计与实现

（1）数量性状表型值的有限混合Laplace分布

假定数量性状在某分离的表型值X为一随机变量，其概率密度为：

（2）有限混合正态分布参数的极大似然估计（MLE）

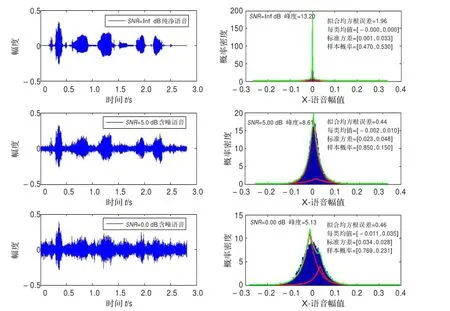
图2 EM仿真结果

（4）极大似然估计EM算法中成分分布数k的确定

EM迭代由确定k开始并完成，对于一个确定的k，EM迭代除了给出所估计的参数外，还给出相应的对数似然函数值lˆk)。

1977年，Akaike根据最大熵原理得出了极大似然函数与熵之间的关系。根据这个关系，有限混合正态分布参数的极大似然估计中，确定k的最佳方案应使AIC准则最小。

3.3 实例仿真

混合模型参与个数k=2，取上述纯语音、含babble噪声信噪比SNR=5，0 dB的语音。EM仿真结果见图2。

纯语音、含babble噪声信噪比SNR=5，0 dB语音的混合Laplace分布模型的平均误差RMS分别为5.38、0.45、0.59，它们的混合Laplace分布模型的平均误差RMS分别为1.96、0.44、0.46，效率分别提升了63.57%、2.22%、22.03%。

4 结束语

本文研究了Laplace分布模型与Laplace混合分布模型，做了理论分析与实验仿真。Laplace混合分布模型阶数的选定值可用AIC、BIC准则确定，也可选密度函数的加权系数确定，先把阶数给得稍大点，若其最小的系数小于5%以下除去这项，这样就把参数估计与确定模型阶数一并进行。为了提高参数估计的软件速度也可采用类似有限混合正态分布[8]估计方法，每步先估计各分密度的均值与方差，再依Laplace分布参数与它们之间的关系求出。本文提出了语音Laplace混合分布建模新思路，这些研究为语音增强、语音编码、语音识别等提供了新的理论基础。

[1]韩纪庆.语音信号处理[M].北京：清华大学出版社，2010.

[2]赵力.语音信号处理[M].北京：机械工业出版社，2009.

[3]周彬，邹霞，张雄伟.基于多元Laplace语音模型的语音增强算法[J].电子与信息学报，2012，43（7）：1568-1573.

[4]邹霞，吴其前，张雄伟.一种基于Laplacian语音模型的语音增强算法[J].信号处理，2007，23（2）：195-199.

[5]Zou Xia，Zhang Xiongwei.Speech enhancement using an mmse short time dct coefficients estimator with supergaussian speech modeling[J].Journal of Electronics，2007，24（3）：332-337.

[6]应娜，赵晓晖，董婧，等.一种谐波正弦语音模型的最佳相位估计算法[J].电子学报，2009，37（4）：860-863.

[7]孙艳，于凤芹.小波多分辨率的谐波正弦语音建模[J].计算机工程与应用，2011，47（17）：151-153.

[8]粱岩，鲍长春，夏丙寅，等.基于高斯混合模型的压缩域语音增强方法[J].电子学报，2012，40（10）：2031-2038.

[9]刘明辉，黄中伟.结合高斯混合模型和VOT特征的音素发音错误检测[J].科学技术与工程，2013（7）：1789-1793.

[10]李德毅，刘常昱，淦文燕.正态云模型的重尾性质证明[J].中国工程科学，2011，13（4）：20-23.

[11]陈琳，刘维奇.重尾分布族及其关系图[J].高校应用数学学报，2009，24（2）：166-174.

[12]Spib noise data[EB/OL].[2013-08-05].http：//spib.rice.edu/ spib/select_noise.html.

[13]Speech&noise data[EB/OL].[2013-08-05].http：//www. utdallas.edu/～loizou/speech/noizeus/.

[14]Dempster A P，Laird N M，Rubin D B.Maximum likelihood from incomplete data via the EM algorithm[J]. Journal of the Royal Statistical Society，Series B（Methodological），1977，39（1）：1-38.

[15]谭鲜明.有限正态混合模型的参数估计与应用[D].天津：南开大学，2005.

HOU Yubao,WANG Jingfang

College of Information Science and Engineering,Hunan International Economics University,Changsha 410205,China

For overweight tail characteristics of the speech signal,this paper proposes a mixed-laplace distribution acoustic model.Laplace mixture distribution model parameter estimation is discussed theoretically,and which can be achieved from the principles and algorithms.The maximum expected（Expectation Maximization,EM）algorithm has been applied to obtaining good results.The hybrid Laplace model has been creatively used to study speech signal processing.

mixture Laplace model;speech signal;Expectation Maximization（EM）;kurtosis;heavy-tailed distribution

针对具有超重尾特性的语音信号，提出了混合拉普拉斯分布语音模型。从理论上探讨了混合拉普拉斯分布模型的参数估计，从原理与算法得以实现。通过最大期望（Expectation Maximization，EM）算法取得了良好效果。创新运用混合拉普拉斯模型研究语音信号处理。

混合Laplace模型；语音信号；最大期望算法；峰度；重尾分布

A

TPl82

10.3778/j.issn.1002-8331.1310-0328

HOU Yubao,WANG Jingfang.Mixture Laplace distribution speech model research.Computer Engineering and Applications,2014,50（18）：202-205.

侯玉宝（1982—），男，讲师，主要研究方向：信号处理。E-mail：matlab_wjf@126.com

2013-10-25

2013-12-15

1002-8331（2014）18-0202-04

CNKI网络优先出版：2014-01-26，http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1310-0328.html