基于优化DRG的三维人体点云骨架提取方法

侯培，田庆国，葛宝臻

1.天津大学精密仪器与光电子工程学院，天津 300072

2.光电信息技术教育部重点实验室，天津 300072

基于优化DRG的三维人体点云骨架提取方法

侯培1，2，田庆国1，2，葛宝臻1，2

1.天津大学精密仪器与光电子工程学院，天津 300072

2.光电信息技术教育部重点实验室，天津 300072

三维模型的骨架通常指模型的中轴，它是一组位于物体中心位置的曲线集合，是物体的一种很重要的拓扑形状描述符[1]，能够清晰地呈现模型的形状信息和拓扑特性，提供模型的语义学信息。因此在模型动画[2]、模型重建[3]、图形检索[4]、图像分割[5-6]和医学图像[7]等很多方面得到广泛的应用和研究。

传统的骨架提取方法一般基于三维体素模型，而由三维扫描仪得到的点云模型散乱且无语义特征，在骨架提取前需要进行处理，变成体素或网格模型。这个过程不仅花费更多时间，而且容易引入噪声，若模型存在漏洞则会给体素化带来一定难度。故诸多学者开始研究直接在散乱的点云模型上提取骨架的方法。

基于Morse[8]理论和Reeb图原理[9]可以提取点云模型的骨架。Verroust A.等人提出了计算3D散乱点云模型的Reeb图，将其作为曲线骨架的算法，该方法适用于具有树状分支的模型[10]；Xiao Yijun将这种在点云模型上提取的Reeb图定义为离散Reeb图（DRG）并应用于人模型的肢体分割[5]；Natali等人将DRG推广为任意维度空间，可以应用在任何形状、任何质量的点云模型上[11]。DRG计算简单，能直接操作由三维扫描仪扫描得到的点云数据模型，得到的结果与原模型的拓扑一致性好。但其在描述模型主体与分支连接区域的骨架时，出现分支部分骨架曲线偏离中轴的问题。

为了改进上述问题，得到更加准确的骨架曲线，本文提出了一种优化方法：提取人体模型的DRG作为初始骨架模型，建立初始骨架的能量函数，在点云模型距离场梯度驱使下不断迭代调整曲线位置直到骨架的能量达到最小，最终将其调整到中轴位置，得到准确的人体点云模型骨架曲线。本文方法得到的骨架曲线能保持较好的连续性和与原模型的拓扑一致性，且位置十分准确。将本文算法应用于各种不同姿势的人体模型，结果表明所得骨架曲线更接近模型中轴位置。

1 基于优化DRG的骨架提取算法

本文算法中提取人体点云模型骨架的过程为：提取点云模型的DRG，将其作为初始骨架线；对初始骨架曲线进行预处理，去除一些噪声点带来的“毛刺”等错误分叉，并对初始曲线进行修正；将预处理后的骨架曲线中分支部位的曲线作为目标段骨架线，建立点云模型的距离场和骨架曲线的能量函数，在模型距离场梯度驱使下不断调整目标段骨架线位置，直到能量函数值最小，从而得到更接近中轴位置的优化DRG骨架曲线。

1.1 点云模型DRG提取

离散Reeb图可以看做是经典Reeb图连续曲线的离散化，由离散节点和连接节点的线段来近似表示曲线。在模型拓扑结构发生分支的部分，细节信息较多，在节点离散化过程中会缺失这些细节表示，从而使得这部分曲线偏离中轴位置。图1为采用本实验室三维人体扫描仪得到的三维人体点云模型，图中的曲线为点云模型的DRG经过预处理后的初始骨架线，曲线上各点为DRG的节点。图1中三个椭圆区域由上到下依次为头部、肩部和胯部的部分区域放大图。头部放大区域显示了由点云模型上噪声引起的一系列毛刺和孤立错误点，这些点使骨架拓扑性存在误差，可能导致分支部位的误判，需要将其去除；肩部和胯部放大区域分别显示了分支部位曲线偏离中轴的情况。这些偏离使得骨架曲线位置不准确，因此需要在保持骨架曲线拓扑性的基础上找到分支部位偏离中轴的骨架曲线段进行优化，调整偏离骨架线的位置，提高骨架提取精度。综上所述，为了得到更准确的骨架，需要对DRG初始骨架进行预处理去除毛刺噪声，然后再对预处理后的骨架曲线优化。预处理后骨架线如图2所示。

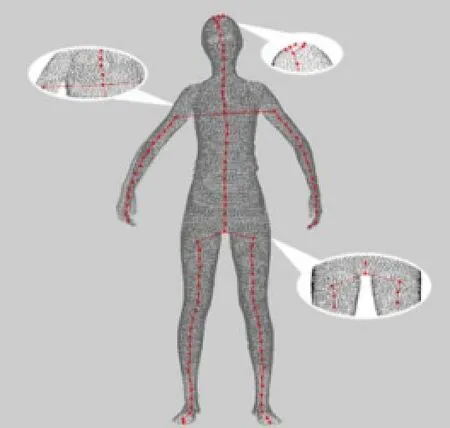
图1 人体三维点云模型DRG

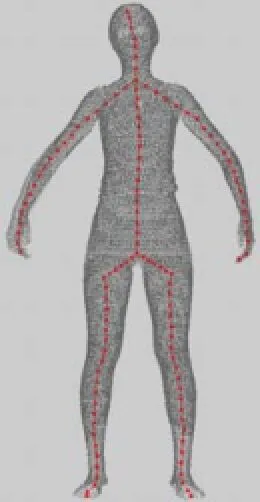
图2 预处理后骨架线

1.2 初始骨架线预处理

在优化之前，先对DRG骨架曲线进行预处理，包括去除毛刺和修正骨架两部分。由1.1节的分析可知，对分支部位的偏离骨架线进行优化前，需要根据DRG中节点连接情况判断分支部位，如DRG上存在图1中头部的毛刺现象，将影响判断的准确性。因此在优化前，需要去除这些噪声点带来的毛刺。去除的过程为：首先，去除没有与其他节点相连接的孤立节点；然后查找分叉节点，如果连接在这个分叉节点上的分支骨架线长度小于某阈值，去掉这个分支骨架线，并重新计算该区间剩余分支线的位置。

骨架预处理的另一个内容是修正骨架线，将曲线中位于体外的部分调整到体内。修正骨架原因有二：对曲线段优化时，需要迭代地移动目标曲线段直到中轴位置，初始目标曲线越接近中轴，需要迭代的次数将越少；由于体内位置距离场值为正，体外位置距离场值为负，迭代过程中要不断判断曲线是否位于体内，这将降低算法的效率。为了减少迭代次数并且减少迭代过程中判断体内体外状态的次数，在初始骨架线预处理阶段就将体外曲线调整到体内从而提高优化算法的运算效率，而且调整目标骨架线的初始位置并不改变骨架最终移动到中轴上这一结果。调整骨架线的方法为：找到分叉点，根据分叉部位拓扑特征决定分叉点调整方向，沿此方向调整一段位移后判断分叉点上连接的分支骨架线是否都在体内，若没有到达体内则循环移动分叉点，直到所有分支骨架线都位于体内时停止。判断空间某点是否在体内的方法为：过该点的平面在人体点模型上截得一个二维图形，在这个二维平面上，判断该点是否在二维图形内部，则可知此点是否在三维模型内部。图2为将图1结果进行预处理之后的结果，此时的结果没有杂散点和毛刺的影响，骨架线全部调整到了体内，优化过程中将不需要考虑体外的情况。

1.3 基于能量最小化的骨架曲线优化

对于预处理后的骨架线，自动找取人体分支部位的多段骨架线作为待优化目标线段，用υ(s)表示其中一段待优化曲线，通过变换曲线形状将定义在该曲线上的能量函数（1）最小化，就能得到更为优化的骨架曲线，能量函数表示为：

其中，L(υ)为待优化曲线的长度，它控制骨架线的形状，使其具有一定的弹性；P(υ)是由能够体现点云模型性质的数据构成的函数，它约束骨架线的位置，其最小值所对应的位置为中轴部位。α、β分别代表各部分权重，根据实验可以确定一个经验值。外力推动初始骨架线发生形变，使其慢慢靠近中轴部位，直至能量函数（1）达到局部极小值，从而得到优化的骨架曲线。

基于上述原理，本文需要找到一个P(υ)表达式，使得当骨架线向中轴位置移动时，其函数值逐渐减小。按照文献[12]中的定义，模型中某点到模型上的最短距离为该点距离场。越接近模型中轴，距离场值越大，距离场的局部极值为模型的中轴所在位置。因此，如果定义距离场的倒数作为P(υ)，则当曲线越靠近中轴，该函数值越小，符合上述要求。

要得到函数P(υ)的表达式，首先需要得到点云模型中任意位置的距离场。在三维体素模型中，文献[13]给出通过距离场变换得到模型中任意位置的距离场值。连续空间中某一点υk的距离场值D(υk)为点υk到模型表面上的最短距离。而在本文的点云模型中，若点云足够密，即点云模型中相邻点之间的距离远小于空间点υk到模型表面的距离时，υk的距离场值近似等于该点与点云模型上最近点的距离值，即

pi为点云模型上第i个顶点。

用MATLAB按照上述方法计算点云模型空间中的距离场值从而证明该方法的正确性。用平面截取图1中点云模型得到一个二维截面，图3（a）中点为所截得大腿部位二维点云，根据本文所述点云模型距离场构造方法，求得平面上各位置的距离场的大小及其梯度值，图3（a）中箭头所示为距离场梯度，可以看出，在模型内部，距离场增大的方向指向中心。图3（b）为对应距离场的三维表示，高度代表距离场的绝对值，高度最低的环形对应图3（a）中点云所在位置。由图3（b）可直观看到，距离场大小分布呈“花蕊状”，在模型内部，越远离点云模型，距离场值越大，距离场值在中轴部位达到最大值；在模型外部，越远离模型，距离场的大小也将增大。初始骨架线经过预处理后，都将位于体内，因此不需要考虑体外情况。由图3可知根据本文方法构造的距离场最大值位于中轴部位。

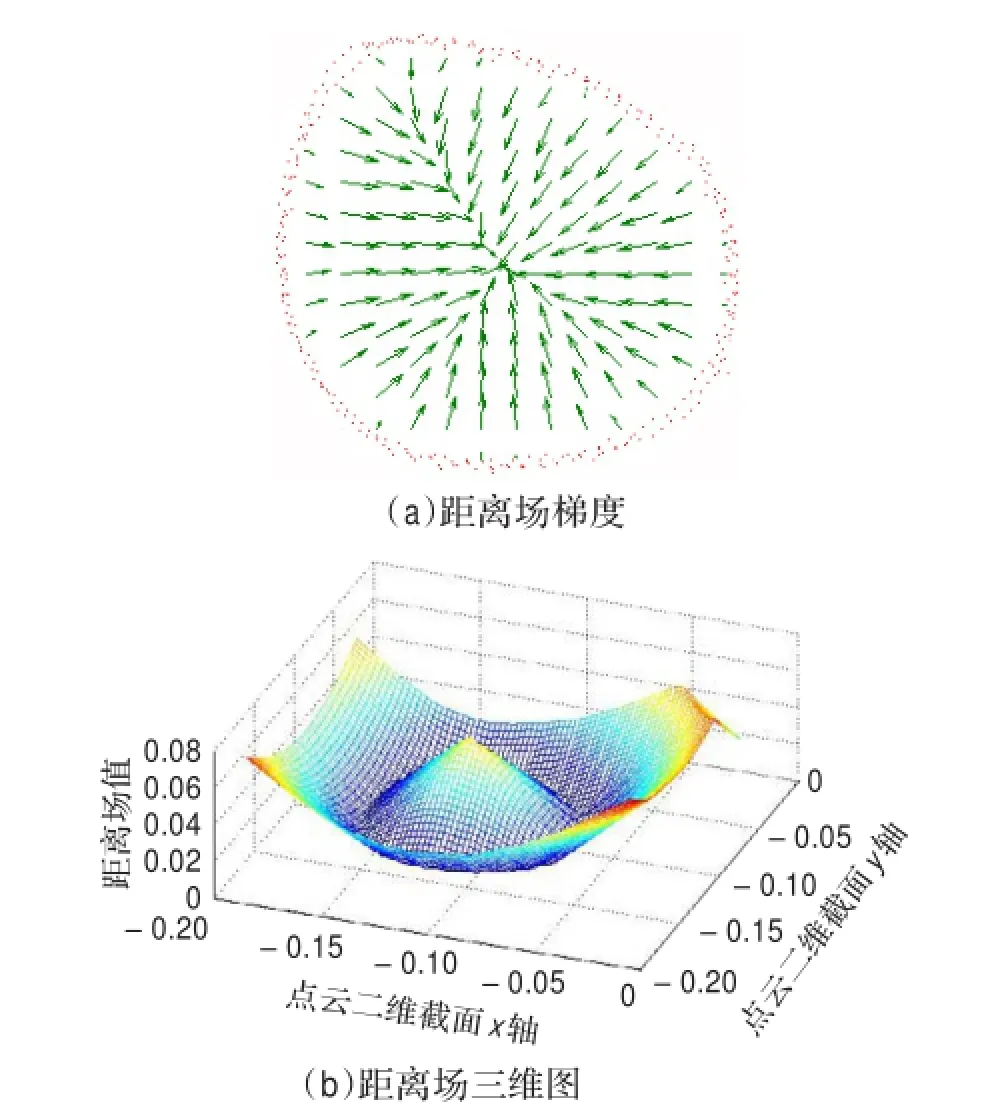
图3 点云模型距离场

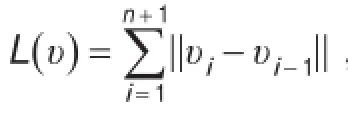
越接近中轴，曲线上各点的距离场值越大，则P(υ)值越小。选取合适的α、β值，在曲线长度L(υ)的约束下，能量函数（1）最小时将得到较为准确的骨架。

目标线段的起点和尾点固定，所有插入点在距离场梯度的推动下逐渐移动，插入点υi的坐标为(υx，υy，υz)，每次移动的位移矢量为(Gx，Gy，Gz)，其中：δ为单位长度，其大小与点云模型相邻点之间的平均距离值为同一数量级。

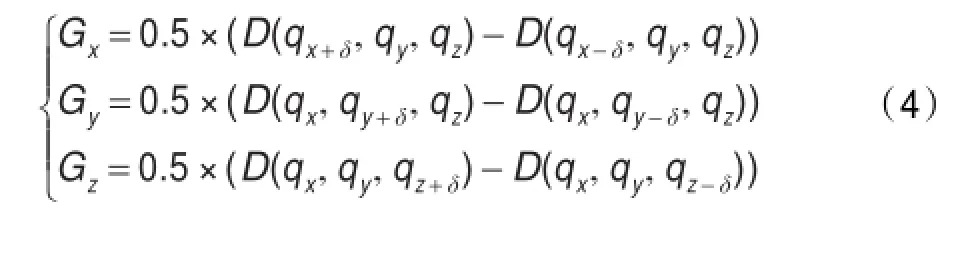
下面是优化算法的具体描述：

（1）根据初始骨架线上各节点的连接情况，找到分支部位的节点，定位人体模型的分支部位。

（2）找到分支部位所有偏离中轴的目标线段，记录目标线段个数N。

（3）以目标线段的两端点为首尾点，在其中均匀地插入n个插入点。

（4）按公式（1）计算初始曲线的能量E0。

（5）按公式（4）计算插入点的移动矢量，将每个插入点移动到新的位置，形成新曲线。

（6）按照公式（1）计算新曲线的能量E1，比较E0和E1的大小。

（7）如果E1≤E0，则将当前E1赋给E0，并循环执行（5）～（6）步骤直到E1>E0为止。

（8）对每条目标线段执行步骤（3）～（7），共执行N次。

经过上面步骤后，目标线段最终成为一条更接近中轴的骨架曲线。图4为应用上述算法对于图1所示人体点云模型肩部各段目标骨架线的优化过程，图4（a）为预处理后的初始曲线，图4（b），（c）分别为优化过程中曲线经过的位置，图4（b）为循环执行20次步骤（5）～（6）后的曲线，图4（c）为循环执行30次的曲线，图4（d）为曲线移动到中轴完成优化的结果。图5为人体胯部各段初始骨架线的优化过程，图5（a）为预处理后的初始曲线，图5（b），（c）分别为优化过程中曲线经过的位置，图5（b）为循环移动20次的结果，图5（c）为循环移动40次的结果，图5（d）为完成优化后的结果。图4和图5形象地展示了对于偏离中轴曲线优化的过程。

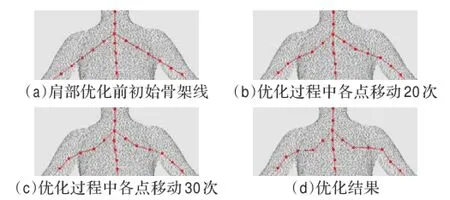
图4 肩部骨架线优化过程

图5 胯部骨架线优化过程

2 实验结果与分析

实验中三维图像文件的读取和显示采用本实验室开发的激光三维表面数字化系统软件包完成。采用的三维人体点云模型是由天津大学自主研制的“激光扫描三维数字化仪”[14]扫描得到。该扫描仪扫描范围为1 m（直径）×2 m（高），分辨率为1 mm（水平）×2 mm（深度）× 2～4 mm（竖直方向可调整），扫描时间为16.7～33.4 s。

2.1 优化前后结果对比

为了验证本文的优化算法所得骨架位置的准确性，对图1所示的点云模型进行实验。选择点云上的测地距离作为标量函数，计算模型的DRG，图1为计算结果。将所得DRG曲线进行预处理，相邻两个节点间的骨架弦长度作为判断毛刺的阈值，剪除“毛刺”分支，以相邻节点作为移动单位，修正骨架线以提高算法的效率，得到图2所示预处理后的骨架曲线。根据节点连接情况找到分支部位曲线段作为目标曲线，对每段目标线段均匀插入5个节点来代表离散化的曲线，优化过程中参数的设置为α:β≈33且小范围浮动不影响优化结果，经多次迭代后得到优化的骨架曲线。图6（a）为DRG曲线，图6（b）和图6（c）分别为优化后的骨架曲线的正面视图和侧面视图，相较于图6（a），图6（b）中曲线位置更加准确，说明本文算法在DRG基础上有效地提高了骨架曲线的中轴性。

图6 针对图1中模型进行骨架提取结果

2.2 同一模特的不同姿势模型骨架提取对比

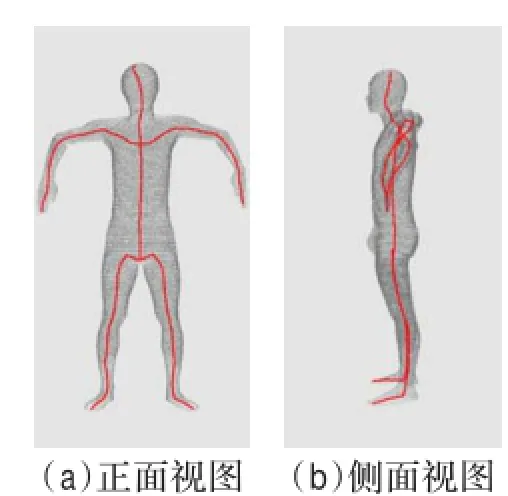
图7 大臂平举姿势模型骨架提取

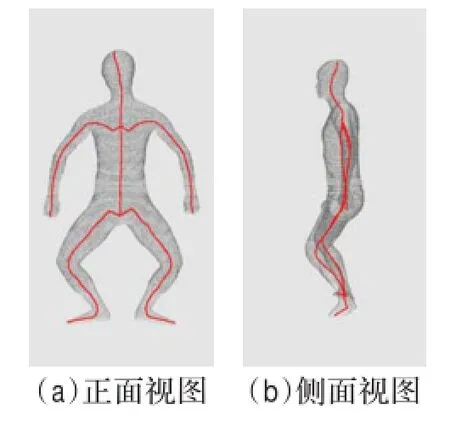
图8 下肢弯曲姿势模型骨架提取

为了说明本文算法在不同姿势下的适用性，在相同环境中对同一个模特扫描了不同姿势的人体点云模型，按照以上过程进行计算并对比结果，图7～图10列出其中四种具有典型特征姿势的实验结果，其中图7～图10的（a）分别为对应姿势模型优化后骨架的正面视图，图7～图10中的（b）为对应优化骨架的侧面视图。

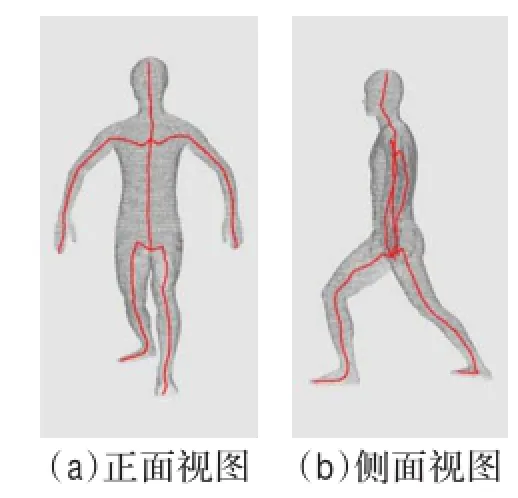
图9 迈左腿姿势模型骨架提取

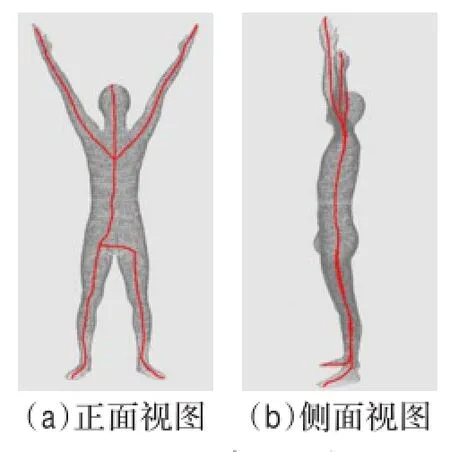
图10 双臂上举姿势模型骨架提取

图7模特姿势的特点是模型中包含一段与身体拓扑方向垂直的拓扑结构，即平举的大臂；图8中姿势的特点是下肢包含较大的弯曲角度；图9中姿势的特点是模型左右腿不对称，左腿向前迈一大步；图10中姿势的特点是上肢拓扑分支向上。将图7～图10中四种不同姿势的模型进行骨架提取所得结果进行对比说明：算法能自动判断不同的分叉类型，准确找到分叉部位中需要优化的目标线段并进行优化；在肢体弯曲角度很大时仍能很好地提取其中轴；能识别较为复杂的拓扑结构，并正确提取其骨架；算法不局限于对称模型。因此本文算法对不同姿势的人体模型具有较高的稳定性。

2.3 不同模特同一姿势模型骨架提取对比

为了验证本文算法对于不同体型模特点云模型的适应性，本文采集了不同体型的模特的多种姿势的点云模型并进行骨架提取。图11为不同体型模特的点云模型骨架提取结果，且模特姿势与图9相同。图11中模特（a）为偏瘦高型的男性，图11（b）模特为偏胖高型的男性，图11（c）模特为偏瘦高型的女性，图11（d）模特为偏胖矮型的女性。由图可以看出，不同体型的模特骨架提取结果略有差异：较瘦的人更容易区分出其胯部和腋下分支，因此提取效果更好，较胖人的骨架在分支部位中轴性略差，但整体来说，提取效果有了较大的提高。结果表明，本文算法能够很好地适应模特体型的变化，提取出中轴性较好的骨架曲线。

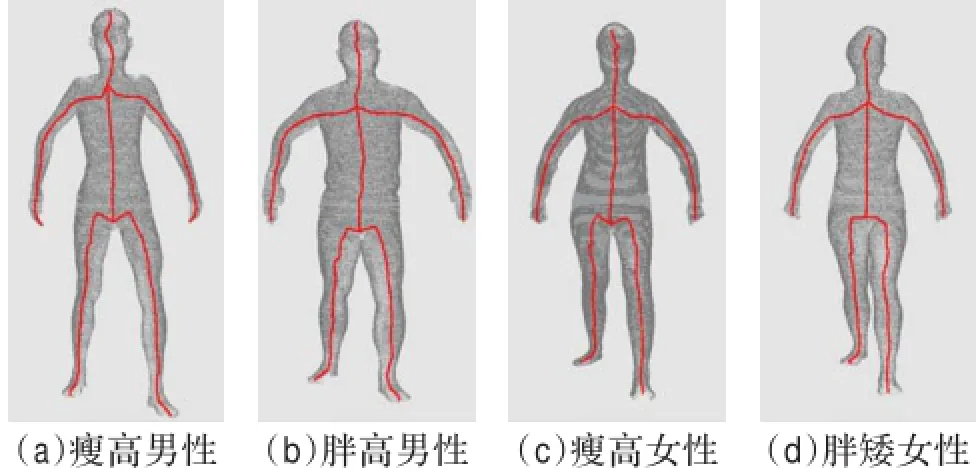
图11 不同体型模型的骨架提取结果

2.4 与其他方法对比

基于拉普拉斯算子的点云收缩的骨架提取方法[15]是近年来较为流行的一种点云模型骨架提取算法。该算法鲁棒性高，受模型的噪声和数据缺失的影响较小，可以广泛地应用在各种模型上。而本文提出的算法主要针对人体点云模型，为了验证本文算法的有效性，将本文算法与近年流行的基于拉普拉斯算子的点云收缩方法进行对比，图12所示为采用拉普拉斯算子的点云收缩方法对图6～图10所示姿势的点云模型处理结果，图12（a）～（e）分别对应图6（a）～图10（a），比较两组结果可以看出：（1）两种算法都能正确地得到模型的拓扑结构；（2）观察五个模型的肩部和胯部分支部位骨架线，文献[15]算法所得肩部骨架线偏低，基于本文算法的骨架线经过优化后，分叉部位更贴合模型表面的变化，中轴性更好；（3）由于本文算法的提取结果较依赖测地距离源点的选择，根据本文算法，图10（a）测地距离源点位于人体左脚部位，导致骨架线上胯部分叉的中心点略有偏移，而图12（e）所得结果提取曲线较为对称，但在人体末端，如头顶部、脚部和手部，文献[15]算法所得骨架线终点没有到达肢体末端，而本文算法所得骨架线在肢体末端更完整。因此，本文算法主要针对人体点云模型，能够准确提取出中轴性较好的骨架曲线。

两种算法所需时间均较为依赖迭代次数，与模型的姿势、形状和算法中参数的设置等因素紧密相关。文献[15]作者给出其算法的MATLAB程序，用该程序对图7模型进行处理提取出骨架线所需时间为2 943.765 s，用MATLAB实现本文算法对该模型的处理，运行时间为2 214.299 s。

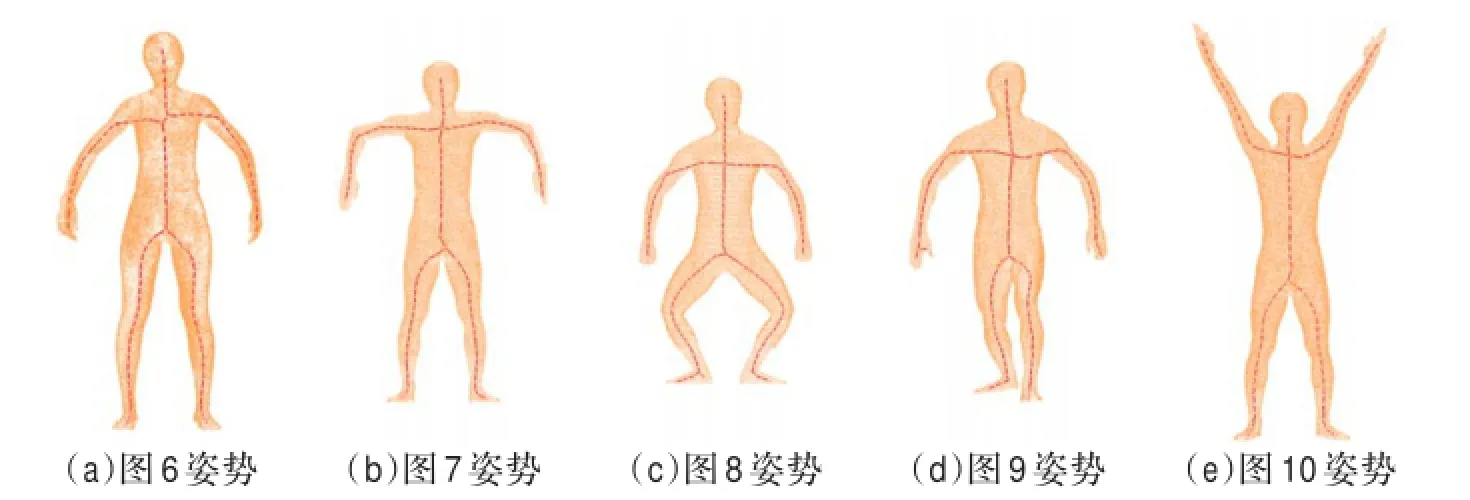
图12 文献[15]算法对各种姿势模型进行骨架提取的结果

3 结束语

本文基于Morse原理和三维点云模型的DRG提取方法，研究了对DRG骨架线进行优化的方法。本文方法可以直接应用在三维扫描仪得到的点云模型上，省去了对点云进行重建等处理的步骤。该方法通过对模型的DRG曲线位置进行调整，采用能量最小化方法将分叉部位骨架线移动到中轴位置，从而得到优化骨架线。实验证明，相比于模型的DRG来说，使用本文方法优化后的骨架曲线更符合人的直观理解，位置更加准确，且本文算法对于三维人体点云模型的变化有较高的适应性。

[1]Wu Jiangui，Duan Hong，Qi Zhong.3D image skeleton algorithms[C]//2011 IEEE International Conference on Anti-Counterfeiting，Security and Identification，Xiamen，China，2011：97-100.

[2]于勇，王兆其，夏时洪，等.一种姿态无关的人体模型骨骼提取方法[J].计算机研究与发展，2008，45（7）：1249-1258.

[3]Serino L，Arcelli C.On the computation of the<3，4，5> curve skeleton of 3D objects[J].Pattern Recognition Letters，2011，32（9）：1406-1414.

[4]Hilaga M，Shinagawa Y，Kohmura T，et al.Topology matching for fully automatic similarity estimation of 3D shapes[C]// Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques.New York：ACM，2001：203-212.

[5]Xiao Yijun，Siebert P，Werghi N.A discrete Reeb graph approach for the segmentation of human body scans[C]// Proceedings of the Fourth International Conference on 3-D Digital Imaging and Modeling，2003：378-385.

[6]Werghi，Xiao Yijun，Siebert J P.A functional-based segmentation of human body scans in arbitrary postures[J].IEEE Transactions on Systems，Man，and Cybernetics-Part B：Cybernetics，2006，36（1）：153-165.

[7]Ding M，Tong R，Liao Shenghui，et al.An extension to 3D topological thinning method based on LUT for colon centerline extraction[J].Computer Methods and Programs in Biomedicine，2009，94（1）：39-47.

[8]Milnor J.Morse theory[M].Princeton：Princeton University Press，1963：1-5.

[9]Reeb G.Sur les points singuliers d’une forme de pfaff completement integrable ou d’une fonction numerique[J]. Comptes Randus Acad Sci，1946，222：847-849.

[10]Verroust A，Lazarus F.Extracting skeletal curves from 3D scattered data[J].The Visual Computer，2000，16（1）：15-25.

[11]Natali M，Biasotti S，Patane G，et al.Graph-based representations of point clouds[J].Graphical Models，2011，73（5）：151-164.

[12]Harry B.A transformation for extracting new descriptors of shape[J].Models for the Perception of Speech and Visual Form，1967，19（5）：362-380.

[13]Wang Jun，Tan Ying.Efficient euclidean distance transform algorithm of binary images in arbitrary dimensions[J].Pattern Recognition，2013，46：230-242.

[14]葛宝臻，孙宇臣.激光三维彩色扫描数字化方法及数字化仪：中国，ZL200510013085.8[P].2005-07-27.

[15]Cao Junjie，Andrea T，Matt O，et al.Point cloud skeletons via Laplacian-based contraction[C]//Shape Modeling International Conference（SMI），2010：187-197.

HOU Pei1，2,TIAN Qingguo1，2,GE Baozhen1，2

1.School of Precision Instrument and Opto-Electronics Engineering,Tianjin University,Tianjin 300072,China
2.Key Laboratory of Opto-Electronics Information Technology of Ministry of Education,Tianjin 300072,China

By minimizing the energy function,the optimization algorithm on the Discrete Reeb Graph（DRG）is put forward to reduce the deviation of the branch skeletal curves from the medial axis.The proposed method takes the DRG of the model as the initial skeleton curve,and later defines an energy function to deal with deviation.The distance field gradient of the scanning data leads the initial skeleton curve to the axis position step by step through iteratively adjusting positions of target curve,and the optimized skeletal curves can be realized when the energy value of the curves is minimized.In the experiments,the proposed method is applied to the scanning data of the same model under four different postures and four different models with the same posture respectively,and it also compares this algorithm with curve skeleton extraction via Laplacian-based contraction.The results verify that the optimized algorithm proposed can adapt to different postures and different body types,and ensure that ultimate curves are closest to the medial axis.Moreover,better descriptions on features of furcation curves can also be obtained.

Discrete Reeb Graph（DRG）;three dimensional human scanning data;extract skeletal curves;minimizing the energy function

针对离散Reeb图（Discrete Reeb Graph，DRG）描述人体骨架时分支部位骨架线偏离中轴的问题，采用了能量函数最小化的方法对DRG曲线进行优化。将人体模型的DRG曲线作为初始骨架，定义其能量函数，在点云模型的距离场梯度的作用下，迭代地调整偏离中轴目标段的曲线位置使其逐渐逼近中轴，能量函数最小时得到优化的骨架。将该算法应用于同一模特四个不同姿势和四个不同模特同一姿势的人体点云模型，并与基于拉普拉斯算子的点云收缩的骨架提取方法进行了比较。结果表明，该算法能够很好地适应各种不同姿势和体型，模型分叉部位的特征得到更加完善的描述，得到的骨架曲线更接近模型的中轴。

离散Reeb图；三维人体点云模型；骨架提取；能量函数最小化

A

TP391

10.3778/j.issn.1002-8331.1210-0243

HOU Pei,TIAN Qingguo,GE Baozhen.Research on method of extracting skeletal curves of 3D human scanning data based on optimizing DRG.Computer Engineering and Applications,2014,50（18）：182-187.

国家自然科学基金（No.61027012，No.61177002）。

侯培（1987—），女，硕士研究生，主要研究方向为三维数字化技术；田庆国（1973—），男，博士，讲师，主要研究方向为机器视觉、图像处理；葛宝臻（1964—），通讯作者，男，博士，教授，主要研究方向为光电检测与处理、激光粒子测量、激光三维彩色数字化技术、数字全息。E-mail：gebz@tju.edu.cn

2012-10-24

2013-05-07

1002-8331（2014）18-0182-06

CNKI网络优先出版：2013-05-24，http://www.cnki.net/kcms/detail/11.2127.TP.20130524.1509.001.html