基于Lattice的验证方环签名改进算法研究

赵洪建，达汉桥，胡元明

1.武汉大学后勤服务集团，武汉 430072

2.武汉大学测绘遥感信息工程国家重点实验室，武汉 430072

3.武汉大学数学与统计学院，武汉 430072

基于Lattice的验证方环签名改进算法研究

赵洪建1，达汉桥2，胡元明3

1.武汉大学后勤服务集团，武汉 430072

2.武汉大学测绘遥感信息工程国家重点实验室，武汉 430072

3.武汉大学数学与统计学院，武汉 430072

随着信息安全技术的不断发展，数字签名技术也得到了广泛关注，相关研究也在逐渐更新，如文献[1]中提出一种基于特定目标的验证方签名安全机制，在此签名方案中，尽管第三方机构尚不能辨别签名源产生于第一签名方还是中间验证方，然而能够辨别其验证签名源出自两者之一。依据此研究结论，文献[2]设计出一种强约束验证方签名安全机制，即SDVS签名机制，此机制是在文献[1]的基础上进一步改进，强制约定只能通过特定验证方才能进行验证签名，这样保证了其私钥数据信息的唯一安全性。文献[3]对SDVS签名机制的安全性、性能效率进行详细分析与研究，即SDVS签名机制保证了无法伪造、无法传递私钥数据信息，同时也保证了第一签名方身份合法性、隐私性等。正是基于这种安全性优势，强约束安全机制逐渐引入到基于特定目标的验证方签名机制中，并使其在B2B、G2G等多种行业领域得到重要应用[4-6]。

依据格结构的高效安全性优点，可将其引入到信息安全公钥密码机制中，能够抵抗多种入侵攻击，如抗量子计算攻击、随机实例困难问题、最难实例困难问题等。所以，基于格结构的密码安全机制逐渐受到研究学者青睐。如文献[7]创造性地提出了在均等条件下的标准小整数解问题与在最差条件下的格结构一类NP问题的困难系数相一致，并给出了详细地结论分析与证明。文献[8]提出了错误学习机制问题（LWE）与最差条件下的格结构一类NP问题的困难系数相等，同样作出了相关分析与证明。文献[9]以格结构理论原理为基础，形成了基于格结构的特定陷门单向函数，同时在随机预言标准模型下，构造出一种新型技术架构的验证方签名安全机制。文献[10]对文献[9]进行了深入分析，在陷门单向函数理论原理基础之上，设计出一种抽样算法。文献[11]对文献[10]设计的抽样算法进行了实践拓展，基于标准模型条件下，将其抽样算法应用于基于格结构的签名安全机制中，并进行了安全性分析与证明。另外，针对随机预言模型条件下出现的安全性不稳定等情况，文献[12]设计出一种基于格结构的验证方签名安全机制。上述现有文献均依据传统签名安全机制进行了相关研究，尽管在某些方面得到了广泛推广，然而其隐藏的安全隐私问题也较为常见。

目前，关于环签名安全机制的分析与研究正处于如火如荼的阶段，环签名安全机制[13]对传统签名安全机制进行模式上的改进与更新，使其在构建标准模型条件下解决更多难解性问题，如基于离散对数困难问题等，并且因此，为了解决现有的数字签名机制在多个应用中出现的各种隐私安全问题，本文利用环签名安全机制代替传统签名安全机制，引入格结构理论原理，结合强约束安全机制，设计出一种基于格结构的强约束验证方环签名改进算法，即L_SRS算法。通过详细安全与性能分析，表明L_SRS算法具有应用高安全性、签名计算高效率性等优点。

1 概念知识

1.1 格结构（Lattice）

预先设定安全系统参数值是n，其非线性关系的数值向量均是列向量，矩阵A的正交化矩阵记作A˜。如下：

1.2 困难问题

关于环签名安全机制的研究是对传统签名安全机制进行模式上的改进与更新，使其在构建标准模型条件下解决更多难解性问题，本文所提算法安全性的理论基础是标准模型条件下的格结构。关于标准模型条件下基于格结构的小整数解问题的困难性，其主要说明如下：

1.3 相关算法

1.4 强约束环签名

环签名安全机制引入强约束概念，主要有以下几个子多项式时间算法组成：

（1）构建系统模型阶段。n是系统模型输入参数值。此部分是用户Ui取得公钥-密钥键值对(PKt，SKt)的过程。注：假定任意Ui都具有随机的公钥数据信息，所以一个Ui对应唯一性的公钥数据信息，如同用户身份ID。

（2）环签名阶段。环结构R⊆S={U1，U2，…，Umax}是已知输入参数，另外，包括签名用户Ui∈R、私钥数据信息SKt与传输信息M，经过操作，输出数据信息是环结构R对传输信息M的签名值x。

（3）强约束验证阶段。输入参数包括环结构R⊆S= {U1，U2，…，Umax}、传输信息M与（2）的输出参数：签名值x。经过操作，输出数据信息是判定结果，即有效验证（Valid）与无效验证（Invalid）。

从上述描述可知，对于一个具有安全性、正确性的强约束环签名安全机制而言，若签名用户Ui∈R保持诚实状态，那么强约束环签名安全机制的第（3）验证阶段其以有效验证（Valid）作为输出结果的概率最大。

2 形式化与模型分析

关于签名安全机制而言，形式化描述与安全模型的分析是至关重要的，接下来将进行简略介绍。

2.1 形式化描述

假定签名用户是WO，特定验证方是NI，那么一个传统的验证方签名安全机制（以SDVS为示例）主要由以下几个重要部分构成，即包括多个子多项式时间算法，如下：

（1）公共系统参数产生部分：n是输入系统安全参数值，para是输出公共系统参数值。

（2）密钥操作部分：para作为输入，产生公钥-私钥键值对(pki，ski)(i∈{WO，NI})。

（3）环签名部分：将第（2）部分输出结果，即公钥-私钥键值对(pki，ski)作为此部分输入，另加入传输信息M，输出结果是签名σ。

（4）验证部分：输入参数包括(pki，ski)、传输信息M以及第（3）输出结果，即签名σ。在签名σ处于Valid状态下，此部分输出结果是接受（Accept），反之拒绝（Reject）。

（5）副本操作处理部分：输入参数包括(pki，ski)、传输信息M，经过此部分操作处理之后，输出结果是与第（3）部分输出的签名σ不可辨别的签名副本数据信息σ′。

2.2 安全模型

一般条件下，签名机制的安全模型具体内容包括以下几个方面，如下：

（1）强不可伪造性。强不可伪造性是在传统无法伪造性基础上，达到了更具安全性要求，即强约定不可伪造性。强不可伪造性只允许WO与NI两者可以伪造相关签名数据信息，此安全性描述可通过一种挑战方-攻击敌方的形式化游戏概括，具体如下：

①构造阶段：首先预执行公共系统参数产生部分，得到para，其次经过密钥操作部分，获取公钥-私钥键值对(pki，ski)(i∈{WO，NI})，与此同时将其(pkWO，skWO)传输给攻击敌方。

②环签名询问-应答阶段：攻击敌方提交传输信息M，挑战方执行环签名部分，输出其有效签名σ，且将其σ回馈给攻击敌方。

③强约定询问-应答阶段：攻击敌方提交签名数据信息对(M，σ)，挑战方执行强约定验证部分，返回输出结果给攻击敌方。

④挑战方执行伪造阶段：此部分输出结果是伪造信息(M*，σ*)，假定签名σ*有效，M*没有再次经过环签名询问-应答阶段，那么攻击敌方战胜了挑战方。

说明6若如上的攻击敌方不存在，那么在形式化游戏中执行时间周期将小于等于t，环签名询问-应答阶段的次数至多是qsign，强约定询问-应答阶段的次数至多是qverify，攻击敌方战胜挑战方的概率将大于等于δ，那么此种强约束验证方签名安全机制对(t，qsign，qverify，δ)具有强不可伪造性。

（2）强不可传递性。对预先设定的传输消息M与签名σ而言，其不管是签名用户WO还是特定环签名验证方NI，对其签名数据信息都是无条件无法传递的。

（3）签名用户的隐私信息安全性。对预先设定的传输消息M与其对应的一个签名而言，不管是签名用户WO还是特定环签名验证方NI，假定无NI私钥信息，那么一个用户需要判定是WO0还是WO1获取了此签名在操作处理上是不可行的，从而保证了签名用户的隐私信息安全性。

3 L_SRS算法

本文以随机预言模型下的相关签名方案为理论基础，提出了一种基于格结构（Lattice）的强约束验证方环签名改进算法，即L_SRS算法，其具体描述如下：

（1）公共系统参数产生部分(Setup(1n))：预先假定相关参数q≥2，m≥6nlgq，传输信息M={0，1}l，选取随机集合矩阵信息C0，C1，…，Cl∈Zqn×m与实体参数向量u∈Zqn；使。那么para={n，q，m，l，C0，C1…Cl，u，L，s}。

4 安全性分析

4.1 正确性

4.2 强不可伪造性

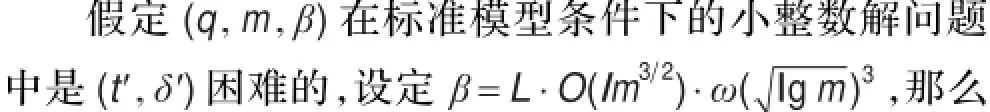
4.3 强不可传递性

4.4 签名用户的隐私安全

由于(NI，p=NIT·s+gmodq)为一个错误学习问题（LWE）示例，NI可采取私钥信息SNI计算得出s向量，那么强约束验证环签名信息e的有效性，但除了NI之外，无任何一方可依据p获取s，反之任何一方都可成功计算求出LWE问题的解，可知任何一方不可能强约束验证签名信息的有效性，从而L_SRS算法保证了签名用户隐私安全。

4.5 安全性比较

现比较已有的标准模型下签名安全机制的相关安全性，对是否具有强不可伪造性、强不可传递性、签名用户的隐私安全性等方面进行了纵向对比分析，如表1所示（注：√表示具有，×表示不具有）。

5 性能分析

本章将从性能效率方面横向比较现有的标准模型下签名安全机制的性能与效率，主要对比点由签名时间、验证签名时间与签名长度等组成。如表2所示（注：l表示签名环数量值；TE、TS表示ExtBasis与SamplePre子算法操作时间周期；TM表示m次向量操作时间周期；k属于正整数常量；m是大于1的正整数；d是随机常量）。

表2 几种标准模型下的类似签名机制性能对比

现对表2中各部分进行详细分析，如下：

（1）签名时间方面：DVS算法的签名时间周期需要m(L+d)TE+m(L+d+1)TS，SDVS算法则在DVS算法基础上通过添加m(L+k-1)次向量操作，实现了无需Ext-Basis子算法处理机制，优化了SamplePre子算法操作流程，签名时间周期减少到只需mTS+m(L+k-1)TM，本文的L_SRS算法继续对SDVS算法进行改进，优化了向量操作处理机制，减少了向量操作时间周期，签名时间周期得到进一步优化，仅需mTS+m(L+1)TM。

（2）验证签名时间方面：现有的签名算法依据理论原理，在验证阶段相关操作仅与向量操作处理机制有关，因此，DVS算法的验证签名时间周期需要m(L+d+1)TM，SVDS算法通过优化DVS算法验证签名过程中的验证流程，减低了验证签名时间周期，只需m(L+k)TM，本文的L_SRS算法融合了SVDS与其他相关签名算法的验证签名优点，实现了验证签名次优化，其验证签名时间周期仅需m(L+2)TM。

（3）签名长度方面：依据相关签名算法原理与签名机制，DVS算法的签名长度是m(L+d+1)；SVDS算法通过对DVS的签名过程优化，其签名长度得到减少，只需m(L+k)+1，本文的L_SRS算法添加了一种强约束安全机制，实现了进一步优化，在保证高签名安全性的前提下，签名长度得到了进一步缩短，仅需m(L+2)。

从上面分析可知，在保证高签名安全性的前提下，本文的L_SRS强约束环签名算法比传统的、在标准模型下的DVS、SDVS签名算法性能效率更高。

6 结束语

本文针对现有的数字签名机制在发放软件著作、专利许可证以及项目工程招投标等应用中出现的各种隐私安全问题，以随机预言模型下的相关签名方案为理论基础，提出了一种基于格结构（Lattice）的强约束验证方环签名改进算法，即L_SRS算法，该算法在标准模型下给出了详实的安全性分析，依据标准的小整数解困难问题，L_SRS算法增加了一种强约束安全机制，能够有效抵抗适应性选择消息攻击，对其具有强不可伪造性。通过安全性与性能分析，本文的L_SRS算法具有应用高安全性、签名计算高效率性等特点。

[1]Ki J，Hwang J Y，Nyang D，et al.Constructing strong identity-based designated verifier signature with self-unverifiability[J].ETRI Journal，2012，34（2）：235-244.

[2]李继国，姜平进.标准模型下可证安全的基于身份的高效签名方案[J].计算机学报，2009，32（11）：2130-2136.

[3]Boyen X.Lattice mixing and vanishing trapdoors：a framework for fully secure short signatures and more[C]//Lecture Notes in Computer Science 6056：Proceedings of the 13th International Conference on Practice and Theory in Public Key Cryptography（PKC’10）.Berlin：Springer-Verlag，2010：499-517.

[4]Alwen J，Peikert C.Generating shorter bases for hard random lattices[J].Theory of Computing Systems，2011，48（3）：535-553.

[5]张建中，郭振，兰建青.一个基于身份的无需可信中心的签名方案[J].计算机工程与应用，2010，46（13）：80-81.

[6]Gordon D，Katz J，Vaikuntanathan V.A group signature scheme from lattice assumptions[C]//LNCS 6477：Proceedings of the ASIACRYPT 2010.Berlin：Springer Verlag， 2010：395-412.

[7]Galindo D，Herranz J，Kiltz E.On the generic construction of identity-based signatures with additional properties[C]// LNCS 4284：Proceedings of the ASIACRYPT 2006.Berlin：Springer-Verlag，2006：178-193.

[8]Stehle D，Steinfeld R，Tanaka K，et al.Efficient public-key encryption based on ideal lattices[C]//LNCS 5912：Proceedings of the ASIACRYPT 2009.Berlin：Springer-Verlag，2009：617-635.

[9]Al-Riyami S S，Paterson K G.CBE from CL-PKE：a generic construction and efficient schemes[C]//Public Key Cryptography PKU 2005：8th International Workshop on Theory and Practice in Public Key Crytography，Switzerland，2005.

[10]Gorantlam C，Saxena A.An efficient certificateless signature scheme[C]//CIS 2005，2005：110-116.

[11]Boneh D，Hanbury M.Generalized identity based and broadcast encryption schemes[C]//Pieprzyk J.LNCS 5350：Advances in Cryptology ASIACRYPT 2008.Berlin：Springer-Verlag，2008：455-470.

[12]Zhao Z M，Wang X Y，Xu C G.An identity signature scheme based on iris information[J].Journal of Electronics&Information Technology，2010，32（10）：2388-2392.

[13]田苗苗，黄刘生，杨威.高效的基于格的环签名方案[J].计算机学报，2012，35（4）：712-718.

ZHAO Hongjian1,DA Hanqiao2,HU Yuanming3

1.Department of Logistics,Wuhan University,Wuhan 430072,China
2.State Key Laboratory of Information Engineering in Surveying,Mapping and Remote Sensing,Wuhan University,Wuhan 430072,China
3.School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China

In order to solve various privacy problems about existing signature schemes,such as issuing software license, issuing patent license and public bidding,in this paper,the random oracle model is the basis theory,and it designs a latticebased strong constraint verifier ring signature improved algorithm（L_SRS）.This algorithm provides detailed security analysis,and it adds a strong constraint security mechanism based on SIS.L_SRS algorithm can efficiently resist adaptive chosen message attack with strong unforgeability.The performance analysis shows L_SRS algorithm has characteristics of shorter signature length,high efficiency and stronger security.

strong constraint;small integer solution;Lattice-based Strong constraint verifier Ring Signature（L-SRS）; ring signature;strong unforgeability

为了解决现有的数字签名机制在发放软件著作、专利许可证以及项目工程招投标等应用中出现的各种隐私安全问题,以随机预言模型下的相关签名方案为理论基础，提出了一种基于格结构（Lattice）的强约束验证方环签名改进算法，即L_SRS算法。该算法在标准模型下给出了详实的安全性分析，依据标准的小整数解困难问题，L_SRS算法增加了一种强约束安全机制，能够有效抵抗适应性选择消息攻击，对其具有强不可伪造性。通过安全性与性能分析，L_SRS算法具有应用高安全性、签名计算高效率性等特点。

强约束；小整数解困难问题；基于格结构（Lattice）的强约束验证方环签名（L_SRS）；环签名；强不可伪造性

A

TP309

10.3778/j.issn.1002-8331.1404-0344

ZHAO Hongjian,DA Hanqiao,HU Yuanming.Improved algorithm research for lattice-based verifier ring signature.Computer Engineering and Applications,2014,50（18）：103-108.

赵洪建（1955—），男，工程师，研究方向为信息安全，高校信息化建设；达汉桥（1956—），男，研究员，研究方向为测绘系统可信化技术；胡元明（1964—），男，副教授，研究方向为数学建模。

2014-04-22

2014-08-07

1002-8331（2014）18-0103-06