基于模糊积分多元决策模型的房地产投资方案优选

徐 畅， 祝彦知

(中原工学院建筑工程学院，河南 郑州 450007)

基于模糊积分多元决策模型的房地产投资方案优选

徐 畅， 祝彦知

(中原工学院建筑工程学院，河南 郑州 450007)

在分析影响房地产投资方案因素的基础上，根据模糊积分的有关理论，对基于模糊测度的模糊积分加以改进，给出基于多层模糊积分的多元决策的房地产投资方案优选模型，并结合某房地产投资方案决策实例验证了该模型的可行性。对实例结果分析表明，在充分考虑影响房地产投资方案各种定性与定量指标的基础上，该优选模型可以更全面、客观地寻求最优房地产投资方案。

投资方案；模糊测度；模糊积分；模糊多元决策；优选

传统数学中，一切概念都是基于确定性与精确性的原则来定义的，然而，由于客观世界的多样性和复杂性，很多事物难以用精确的、确定的概念来描述。模糊数学的诞生为描述这类边界不清的事物提供了一套有效的方法[1-2]。而模糊决策作为模糊数学的一种具体的应用方法，在解决工程实践多目标决策问题中得到了广泛应用。

在房地产开发投资中，投资方案的优选是项目前期的核心工作之一。影响房地产投资方案的因素是多方面的，而且具有复杂性和不确定性，在这些因素中，有些因素是可以量化的，如投资总额、财务净现值等，而有些因素存在模糊性只能给出主观的定性分析，如风险程度、市场效应等[3-4]。为了能全面客观地考虑各种主客观因素的影响以解决房地产投资方案多元决策问题，引入模糊数学中分层模糊积分理论是一种有效的途径[5]。

根据模糊积分有关理论，首先根据决策系统中各因素的性质及其间逻辑关系将其层次化，构造各决策单元的指标体系[6]，其次，根据满意度定义和计算公式对各决策指标进行无量纲化处理，使不同因素间具备可比性，最后基于模糊测度的模糊积分加以改进，对决策单元的指标进行合成处理，推导出模糊积分多元优选模型，可以全面客观地解决房地产投资方案的优选问题。

1 基于模糊积分多元决策的房地产投资方案优选原理

有关模糊测度和模糊积分的相关基本理论在有关文献中做了详细介绍[5-6]，应用模糊积分多元决策模型的房地产投资方案优选基本原理与步骤如下：

(1)取所有备选的投资方案为备择对象集V，V={V1,V2,…,Vq,…，Vl}，共有l个投资备选方案，Vq代表第q个投资方案，列出影响投资方案优选的各个侧面的所有单因素指标集X(因素集)，即X={x1,x2,…,xi,…，xn}，xi代表第i个单因素指标。

(2)作因素集X的P划分，得到X/P={X1,X2,…，Xj,…,Xm}，记Xj={xj1,xj2,…,xjk,…,xju}，P划分的多少需要视具体问题的性质而定，一般可分为两层即可，第一层根据影响房地产投资方案的指标特征将指标分为若干大类，第二层为各类指标中所包含的详细条目。P划分完成后，聘请相关领域有经验的专家学者和技术人员对X/P中的每一个因素集合Xj和Xj中的xjk(k=1,2,…,u)给出其模糊测度，模糊测度的确定方法参见张德利的模糊积分论进展论述[7]。

(3)参阅程楠的《深基坑支护体系的模糊积分多元决策研究》一文观点[8]给出的满意度公式计算各备择对象Vq(q=1,2,…,l)中各因素指标xjk的满意度值，为避免逻辑加权法模糊积分的局限性[8]，根据具体问题对模糊积分模型加以改进，得到应用模糊积分多元决策模型进行房地产投资方案优选的计算模式：

计算X/P中每一个因素集合Xj的Ej(j=1,2,…,m)，其中，

(1)

g(A(k))=g(x(1))+g(x(2))+…+g(x(k))

(2)

(4)一层次的决策结果Ej作为二层次决策的依据，二层次决策重复一层次决策步骤，求出Xj的满意度值，得到系统的模糊积分综合决策：

(3)

式中：g(A(j))=g(x(1))+g(x(2))+…+g(x(j))；Eq代表第q个房地产投资方案的模糊积分综合决策值。

(5)将Eq带入满意度公式[7]，求出h(Vq)，即为第q个房地产投资方案的最终相对满意值。

2 实例分析与讨论

为了验证上述计算模型的合理性，并便于同孙海涛的观点[3]进行比较，以某房地产企业的开发规划为例进行分析。该项目有4个投资方案可供选择，各方案年度指标的测算结果如表1所示。

表1 房地产开发年度经济指标

根据分层模糊积分决策模型，取备择对象集V={V1,V2,V3,V4}，分别代表四个投资方案。每个备择对象共有10个指标因素，即因素集X={x1,x2,…,x10} ，对X做P划分X/P={X1,X2,X3,X4}。采用上述g值的确定方法，根据对各指标相对重要程度的分析，经十位专家综合评定，确定出所含因素的模糊测度g值表(见表2)。

由上述实例可以看出，影响房地产方案优选的指标因素众多，且随着方案的增多，手工计算将难以实现，根据上述原理编制计算程序进行计算。一层次各方案各指标xji的计算结果见表3

根据上述式(1)、(2)、(3)计算得到各方案系统的模糊积分综合决策值Eq={2.220,2.157,1.617,2.054}，将Eq再次带入满意度公式[8]，最终得到各个方案的相对满意度值h(Vq)={h(V1),h(V2),h(V3),h(V4)}={1.000,0.971,0.690,0.922}。由计算结果表明，投资方案的相对满意度顺序为T1>T2>T4>T3，T1为最优方案，T2相对满意值较大可作为备选方案。

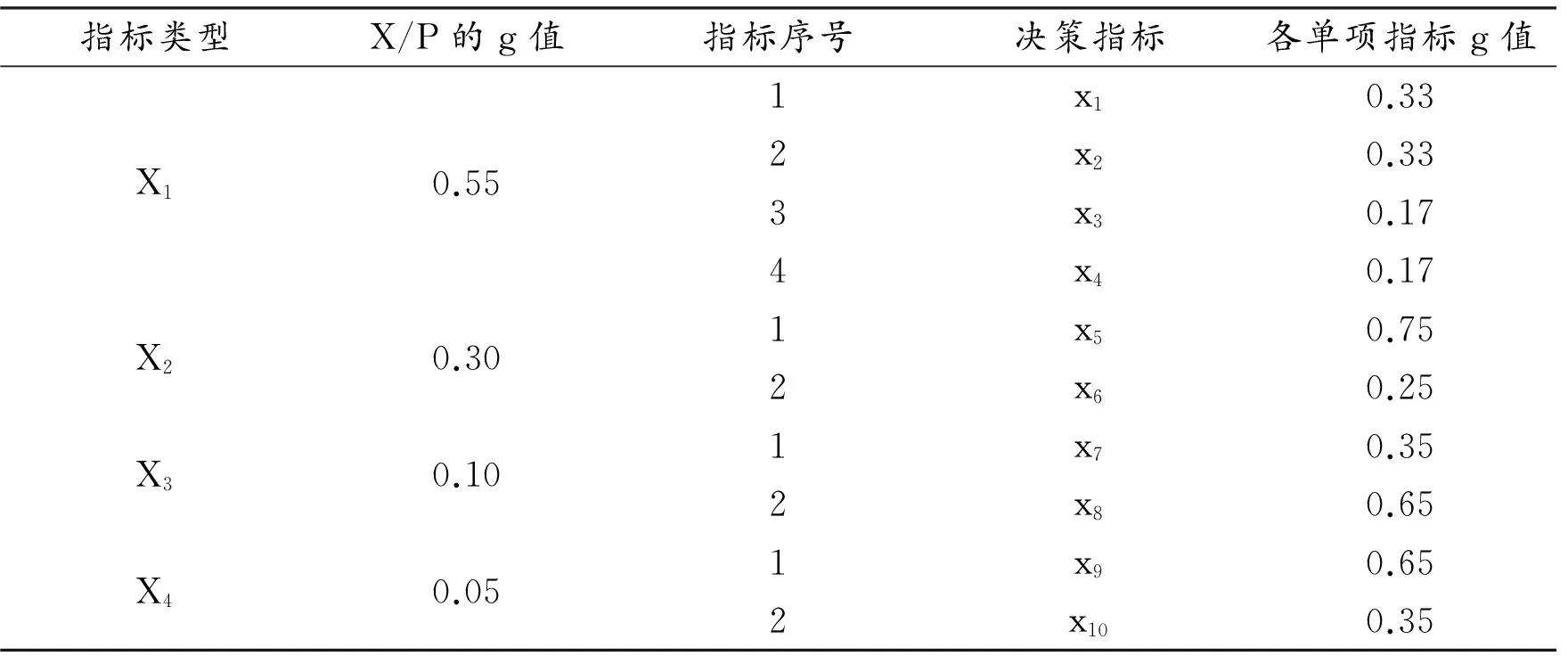
表2 因素集P划分和各因素模糊测度g值

表3 各房地产投资方案各指标的标化值和满意度

3 结语

本文的计算结果与孙海涛的观点[3]是一致的，证明该方法的可行性，且该方法更具先进性，具体体现在：

(1)该优选模型用直观的模糊测度去度量模糊事件，更全面客观地考虑房地产投资方案优选工程中各种定量与定性指标的影响。

(2)该优选模型利用满意度函数在标化值的基础上对决策系统中各定量与定性指标进行满意度的模糊描述，这种无量纲化处理方式使不同指标间具备可比性，这是标化值本身很难做到的。

(3)该优选模型结合模糊积分方法将逻辑加权法发展为积分合成法，不仅能统筹全局而且强调了各指标之间的交互作用，避免了其他模糊多元决策方法中淹没次要因素、失掉重要信息的缺陷。

[1] 方述诚，汪定伟．模糊数学与模糊优化[M]．北京：北京科技出版社，1997．

[2] 李鸿吉．模糊数学基础及实用算法[M]．北京：北京科技出版社，2005．

[3] 孙海涛．基于AHP的房地产投资方案模糊优化模型及应用[J]．企业经济，2011(5)：167-170．

[4] 李友谊，陈学广．企业投资方案的多目标模糊优选决策[J]．科技进步与对策，2004(3)：10-15．

[5] 朱传军．基于模糊测度与模糊积分的房地产评价方法与应用[M]．北京：北京科技出版社，2011．

[6] 哈明虎，杨兰珍，吴从炘．广义模糊集值测度引论[M]．北京：北京科技出版社，2009．

[7] 张德利，郭彩梅，吴从．模糊积分论进展[J]．模糊系统与数学，2003，17(4)：1-10．

[8] 程楠，祝彦知．深基坑支护体系的模糊积分多元决策研究[J]．系统工程理论与实践，2002，22(8)：121-126．

Optimal choice for investment plan of real estate based on fuzzy integral multi-index decision

XU Chang, ZHU Yan-zhi

(SchoolofCivilEngineering,ZhongyuanUniversityofTechnology,Zhengzhou450007,China)

Based on the analysis of effect factors about investment plans of real estate, the multiple-stage and multi-objective fuzzy integral decision model about definitive set are presented by improving the fuzzy integral on the basis of fuzzy measure in a calculating program for applying the model to solve multi decision-making problem. The feasibility of the model is verified through a real estate investment plan optimization of practical engineering. With the result of the given example analysis, fully considering the effect factors of real estate investment plan on the basis of a variety of qualitative and quantitative indicators, this model can be used to optimize the investment plan of real estate more comprehensively and objectively.

investment plan; fuzzy measure; fuzzy integral; fuzzy-multi-index decision; optimum

2013-11-05

徐 畅(1990-)，女，河南太康人，中原工学院建筑工程学院硕士研究生。

1674-7046(2014)01-0082-03

F293.3

A