安徽省小学生体型分类及号型设定研究

许平山，高云兵

（安徽职业技术学院 安徽 合肥 230051； 安徽三联学院 安徽 合肥 230601）

安徽省小学生体型分类及号型设定研究

许平山，高云兵

（安徽职业技术学院 安徽 合肥 230051； 安徽三联学院 安徽 合肥 230601）

针对小学生身体特征发育提前，为使小学生的服装与体型发育相适应，以小学生为对象，对安徽地区1090名7～12岁小学生进行人体测量.通过接触式测量和影像测量两种方法获取小学生人体尺寸，影像测量法主要是测量肩斜，对测量的尺寸数据运用 SPSS统计软件进行了描述性统计分析、因子分析、BMI变量分析、相关性分析等统计分析，获得安徽地区小学生体型特征.将7～12岁小学生体型分为N1、N2、N3型.建立各年龄段的小学生号型标准.以利于小学生健康发育成长.

学龄女童；体型特征；统计分析；体型分类

随着生活水平逐渐提高，小学生的生长发育状况有了很大变化，虽然 1981年国家出台了统一的小学生服装号型标准，1991年进行了修订，1997年又增加了婴幼儿的号型标准，但其控制部位数据已无法符合小学生的实际体型.本文抽取安徽地区 7～16岁女童样本 586个，对 10个部位进行测量，这些部位的数据能够用于服装的样板设计与生产.

1 实验部分

1.1 测量样本

测量样本分布于安徽省合肥市、安庆市、阜阳市，时间安排在 6—7月和 9—10月，分别在合肥市江淮学校、安庆市东风路小学和阜阳市阜阳附小进行.样本数量依据统计学抽样方法确定，在允许误差 1.0cm的前提下，每个城市大于150人，共计 1090名小学生，确保样本分布合理.

1.2 测量方法

由于样本分散，此次人体测量采用接触式手工测量，主要测量工具采用身长计和软尺等标准测量工具.测量在室内进行，温度为 22～25℃，湿度为 40%～60%，保证被测者人体感觉舒适，呼吸自然.被测者统一穿着贴身内衣，测体者进行统一培训，采取单人单项测量，使误差降到最低限度.依据研究目的选择测量项目，选择与人体体型相关的部位测量，包括人体高度、围度和宽度.本文主要研究小学生体型特征，参考 GB16160—1996《服装人体测量的部位与方法》，选择人体的19个部位进行测量.

2 数据分析

2.1 数据描述统计

真实、精确、完备的人体测量数据是进行人体数据化分析的前提和基础，也是设计和制作服装的依据.由于在测量中存在主客观方面导致的误差，因此在正式分析人体测量数据之前对测量数据进行初步的确定和核实，确定数据的异常值和缺失值，剔除其中的不良样本.经过初步处理后确定 1090个有效样本，其中 530名男生，560名女生，用 SPSS软件进行处理，分析学龄小学生的体型特征.各测量项目的均值反映了 9～10岁女童体型各部位的平均水平和整体体型特征.9～10岁女童体型特征的各部位数值的均值、极大值、极小值和标准差.

平均值可以反映所有被测者某个部位的平均水平，但不能全面反映被测者该部位测量结果的状态.标准差反映测量数据偏离样本均值的程度，标准差越大，表明数据偏离越大、越分散，彼此之间差异越大；标准差越小，说明测量数据越集中，彼此之间差异越小.颈椎高标准差最大，其次是胸围、臀围、腰围和身高的标准差较大.因此 9～10岁女童体型变化较大的部位是胸围、臀围、身高和腰围.

为了比较身高、颈椎高、臀围、胸围、腰围离散程度的大小，进一步计算了它们的变异系数，其结果如表1.变异系数的计算公式为：

其中：c是变异系数，x¯是平均值，s是标准差.

表1 臀围、胸围等部位的变异系数

由表1可以看出，胸围的变异系数最大，为 5.9，表明胸围的离散程度最大；其次是臀围（5.4），腰围（5.1），颈椎高（3.2），身高（2.2）.由此可见，9～10岁女童体型变化较大的部位依次为胸围、臀围、腰围、颈椎高和身高.

2.2 因子分析原理

因子分析就是利用少数几个因子来描述许多指标或因素之间的联系，以较少几个因子来反应原资料大部分信息的统计方法.测量的人体部位较多，为了便于分析小学生体型规律，将这些测量指标数目进行有效地简化，通过因子分析可减少分析量负担.一般有四个步骤：

（1)明确待分析的原有若干变量能否适合于因子分析需要；

（2）构造因子变量；

（3)充分利用旋转使得因子变量更具有可解释性；

（4)计算因子变量的得分.

2.2.1 女童体型因子分析

以 9～10岁女童为例，利用因子分析方法找出人体部位主要规律.第一步判定各变量是否适应因子分析，就是计算变量之间的关系系数矩阵.通过查找相关系数计算结果可知，大多数系数都大于 0.5(除肩斜、胸臀差).根据 KMO的检验和 Bartlett球形检验结果，其中 KMO值为 0.905，根据统计学家 Kaiser给出的标准，当 KMO取值大于 0.6，适合作因子分析.见表2.

表2 KMO和 Bartlett检验

第二步构建因子变量，基于主成分模型的主成分分析法是常用的一种因子分析方法，下面用其方法进行分析.

表3 因子提取和旋转结果

表3中第一列式最终因子提取数理为 4个.第二列是从初始变量中提取4个因子变量的特征值，它是衡量因子重要程度的指标.第三列是各最终因子变量对原变量的方差贡献率，第五至第七列是旋转因子对变量总体的刻画情况.

图1 因子分析碎石图

图1是公共因子碎石图示.它的横坐标是因子数，纵坐标是因子的特征值.显而易见前面 4个公共因子的特征值的变化较明显，之后因子特征值的变化趋于平缓.所以说明了提取4个公共因子是可以对原始变量的信息描述有显著作用，能够基本反映原变量的方差.之后以方差极大方法对因子载荷矩阵旋转，以求更好解释因子变量含义，得出旋转后的载荷矩阵数据.

从上面分析可以看出如下特征：

（1）第一主成分主要反映了胸围、腰围、臀围等测量项目，反映身体上、下围度的测量项，称为围度因子.

（2）第二主成分主要反映了身高、颈椎高、全裤长、臂长、下裆长等测量项目，反映身体的长度的测量项，称为长度因子.

（3）第三主成分为胸宽、背宽、肩宽、背长等反映躯干部分的测量项目，反映身体肩胸等躯干的立体形状，称为躯干因子.

（4）第四主成分主要反映了体重、BMI等测量项目，反映身体总体特征的测量项目，称为体型因子.

用这4个主成分因子代替原来的测量项目，可以概括原始测量项目所含有信息的 67.672(4个主成分的累积贡献率为 67.672%)

2.3 体型分类方法的选择

目前的对人体体型分类的方法主要有：

（1)围度差：人体围度主要指胸围、腰围、臀围，它们一般不会保持同步变化.从中体现了不同的体型特征，因而可以将其作为评判不同体型的依据.这种方法被较多标准所使用，如 GB、JIS等.我国是以胸腰差来划分体型的，日本的成年男子以胸腰差来划分体型，而成年女子是以胸臀差来划分体型的.

（2）长度差：主要以前腰节长和后腰节长的差值来划分体型的，因为这个数据最能反映正常体型与特殊体型（挺胸、凸肚和曲背）间的差异.同时该差也是结构设计中重要的因素.但该差主要反映的是上体的体型特征，对下体无法表示，一般只应用在研究中.

（3）各种相关人体尺寸的指数.如，体重与身高的比（丰满度），BMI（肥胖度），围度与身高的比，不同部位的围度比等.但总体上计算不方便，也不直观，对体型的细分有一定的研究价值.在本研究中发现体型在小学生阶段与年龄相关性很高，从图 4-2中可以看出 BMI在各年龄段的发展不均衡性，使得以 BMI在体型方面的研究的必要性.

2.4 小学生 BMI频率分布图

图 2 女童的 BMI变量直方分布图

从图 2看出，7～12岁女童 BMI范围在 12～22，频率最大的 BMI为 14～18左右，经计算得出，女童 BMI差平均值为2.6，标准差 1.8，且服从正态分布.

2.5 小学生体型划分

从图 2中可以看出小学生的 BMI分布（图 2-4和图2-5）以及计算得出，大多数小学生的 MBI集中在 13.5--20间，其中女童集中在 13.5--19，男童集中在 14.5--20间，并且基本按年龄分布.

通过以上分析，7～12岁小学生女童 BMI在 13.5～20，将体型分为 3组，BMI分别为 13.5～15.9，16～17，17.1～19；小学生男童 BMI在 14～20间，将体型分为 3组，BMI分别为14.5～16.9，17～18，18.1～20，如表 4.

表4 小学生体型分类代号及范围

2.6 7～12岁女童服装号型系列确定

表 5 女童中间体的均值调整值(单位：cm)

表 6 男童中间体的均值调整值(单位：cm)

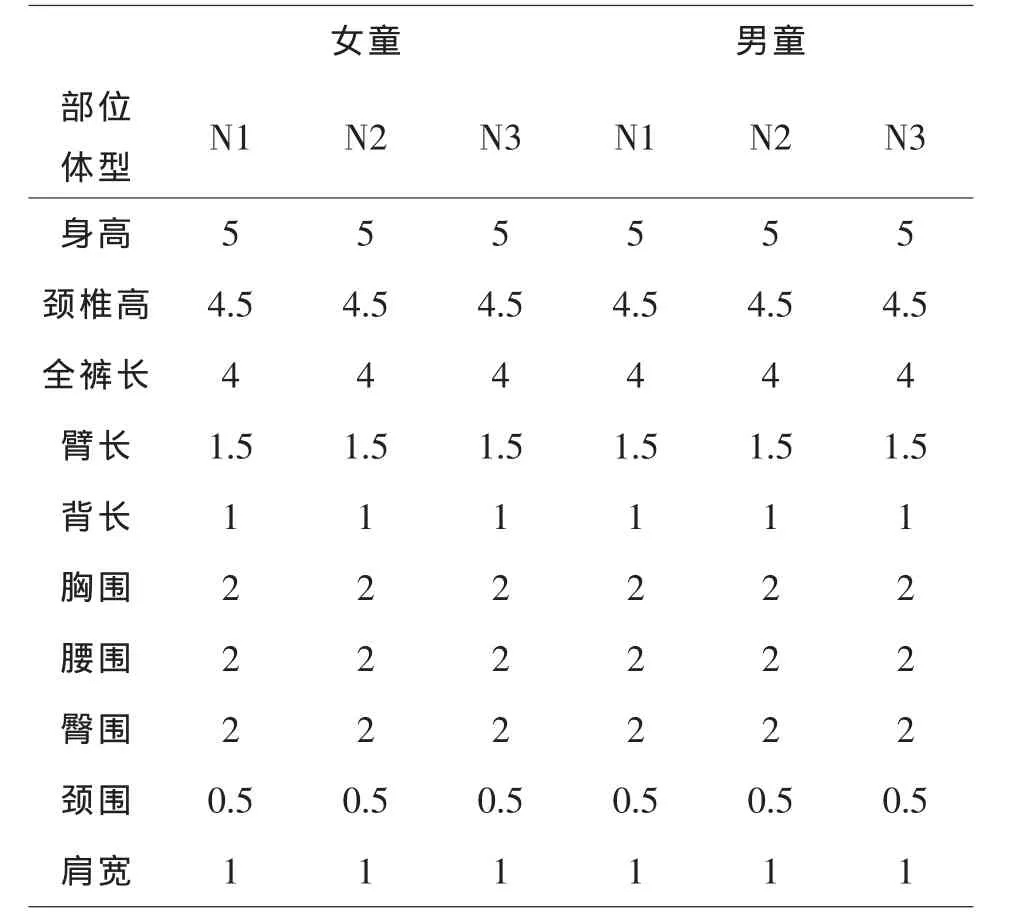
表 7 小学生各体型部位分档采用值表(单位：cm)

依据我国服装号型设计的基本原则，并按照 7～12岁小学生身高的最大值与最小值范围，以及满足覆盖绝大多数人体的原则，测出 7-12岁男女小学生中间体的均值和小学生各体型部位分档采用值表，生产厂家根据分档数值表就能够推导出不同男女小学生的身体部位的具体尺寸，有效的指导生产.小学生中间体的均值和各体型部位分档采用值表见表 5、6、7.

3 结论

从小学生人体数据和小学生服装号型研究两方面入手，通过收集我国安徽地区 7～12岁小学生人体数据，并运用数理统计方法，对小学生服装号型的制定进行了探索性分析与研究，对于以小学生为目标市场的生产厂家组织生产有着重要的指导意义.

〔1〕高云兵.安徽地区小学生年龄段小学生体型分类与上装原型研究[D].上海:东华大学,2013.

〔2〕夏蕾.上海地区7～16岁女童服装号型研究[J].上海纺织科技，2009，37(9):4-6.

〔3〕杨允出,陈敏之,邹奉元.基于三维扫描数据的女性体型特征参数分析[J].纺织学报，2009，30(8):117－122.

〔4〕张文斌,方方.服装人体工效学[M].上海:东华大学出版社，2008.

〔5〕戴鸿.服装号型标准及其应用[M].北京:中国纺织出版社,2004.4.

〔6〕邹奉元,丁笑君,潘力丰.青年女子体型的特征指标及岭回归预测研究[J].纺织学报，2006，27(4):56－59.

〔7〕邹平.逐步回归中服装结构设计数学模型部位间的影响关系[J].纺织学报,2007,28(2):95-9.

TS941.17

A

1673-260X（2014）08-0061-03