Zeros of the Jones Polynomial for Torus Knots and 2-bridge Knots

HAN You-fa,ZHANG Rong-wei,WANG Lin-lin,MA Xiao-sha

(School of Mathematics,Liaoning Normal University,Dalian 116029,China)

Zeros of the Jones Polynomial for Torus Knots and 2-bridge Knots

HAN You-fa,ZHANG Rong-wei,WANG Lin-lin,MA Xiao-sha

(School of Mathematics,Liaoning Normal University,Dalian 116029,China)

We study zeros of the Jones polynomial and their distributions for torus knots and 2-bridge knots.We prove that e(2m+1)πi/2and e(2m+1)πi/4(m is a positive integer) can not be the zeros of Jones polynomial for torus knots Tp,qby the knowledge of the trigonometric function.We elicit the normal form of Jones polynomials of the 2-bridge knot C(−2,2,···,(−1)r2)by the recursive form and discuss the distribution of their zeros.

Jones polynomial;zeros;torus knot;2-bridge knot

§1.Introduction

The main subject of the knot theory is the classif i cation of knots.Knot polynomials play very importance role.Alexander polynomial[1]is a milestone in the knot theory,but it can not distinguish a knot and its mirror.In 1984,Jones[2]has found a new knot invariant(later,it is called Jones polynomial),it is an ambient isotopy invariant,and the calculation is convenient. His f i ndings made the knot theory known as one of the focus at the mathematical f i eld in the world.In[3],Kauf f man computed the Jones polynomial of the torus knots Tp,q(where (p,q)=1))by dif f erent means.In[4],Eunju Lee,Sang Youl Lee,Myoungsoo Seo gave the Jones polynomials of the 2-bridge knot C(−2c1,2c2,···,(−1)r2cr)by the recursive form.In [5-9],they discussed the distributions of the zeros for knots and the relations between Laurent polynomials and Jones polynomial.In[7],Wu F and Wang J pointed the zeros of the Jones polynomial of the torus knots Tp,q(where(p,q)=1))are distributed on the unit circle,but ifthe points of the circle are zeros of the Jones polynomial?In section 2,we give the properties of the Jones polynomial of knots and discuss the zeros of the Jones polynomial of torus knots. In section 3,we give the normal form of the Jones polynomial of the 2-bridge knots and discuss zeros distribution.

§2.The Zeros of the Jones Polynomials of Torus Knots

Def i nition 2.1Let p be a positive integer and q be a nonzero integer,we stand side by side p parallel lines on the normal torus in the space,and move to right by q times after a circle round before meeting the original thrum,then we get a graph,it is called torus knots, and denoted by Tp,q.If q is negative,then move to left,not to right.

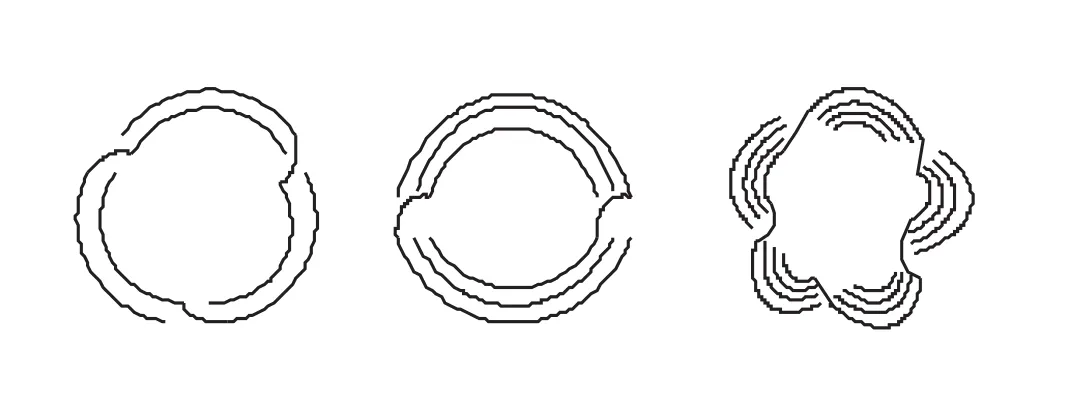
Figure 1Torus Knots

From the projective diagram,one can obtain the properties of the torus knots Tp,qas follows.

(1)Let p and q be relatively prime,then Tp,qare knots;

(2)If d is the maximum common divisor of p and q,then Tp,qare links with d components.

Lemma 2.1[7]If p and q are relatively prime,then

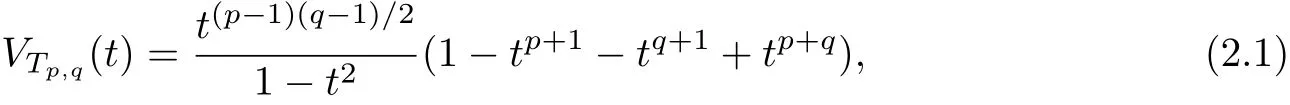
where Tp,q(t)is the Jones polynomial of Tp,q.

Lemma 2.2[7]The zeros of the Jones polynomials for torus knots Tp,q(where(p,q)=1) are distributed on the unit circle|t|=1.

But not all of the points on the unit circle are the zeros of the Jones polynomials for torus knots Tp,q.In[8],Tao pointed that 1,±e2πi/3and eπi/3are not the zeros of the Jones polynomials for any knot.Are there other points that are not the zeros of the Jones polynomials?

Lemma 2.3[7]Let k,p and m be positive integers,only t2m-1+1 and t2k−t2k−1+···−t+1, k/≡1(mod3)are possible factors of the Jones polynomials.In other words,if a root of unity is a zero of the Jones polynomials,then it must be either e(2p+1)πi/2m-1or e(2p+1)πi/(2k+1), k/≡1(mod3).

Theorem 2.1e(2m+1)πi/2and e(2m+1)πi/4(m is a positive integer)can not be the zeros of the Jones polynomials for torus knot Tp,q.

ProofBecause Tp,qis a knot,(p,q)=1.

Firstly,we prove e(2m+1)πi/2(m is a positive integer)can not be the zeros of the Jones polynomials for torus knots Tp,q.

(1)By the period of the Sine function and the Cosine function,we want to prove e(2m+1)πi/2can not be the zeros of the Jones polynomials for torus knots Tp,q,only need to prove eπi/2and e3πi/2can not.We prove e3πi/2=−i can not be the zeros.

We know i4k=1,i4k+1=i,i4k+2=−1,i4k+3=−i(k is an integer).

Since

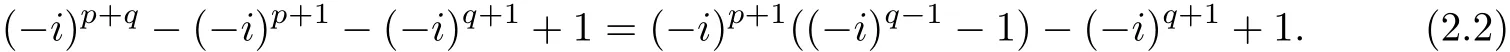
One can get the following facts.

(i)When q is an odd number(since(p,q)=1),then p can be an odd number or an even number),the formula(2.2)becomes the following situation.

But(−i)p+1∈{−i,−1,i,1},iq−1=±1,iq+1=∓1,then the formula(2.3)is±2 or±2i, does not equal 0.

(ii)When q is an even number(since(p,q)=1),now p must be an odd number),the formula (2.2)is as follows. But ip+1∈{−1,1},iq−1=±i,iq+1=∓i,then the formula(2.4)is 2,±2i,does also not equal 0.

In one word,the formula(2.2)is not zero,so the formula(2.1)is not zero,that is e3πi/2=−i can not be the zeros of Jones polynomials for torus knots Tp,q.

Similarly,applying the thought of classifying discussion,we can prove eπi/2=i can not be the zeros of the Jones polynomials for torus knots Tp,q.

(2)We want to prove e(2m+1)πi/4(m is a positive integer)can not be the zeros of the Jones polynomials for torus knots Tp,q,only need to prove eπi/4,e3πi/4,e5πi/4,e7πi/4can not be the zeros.At f i rst,we prove eπi/4can not be the zeros.

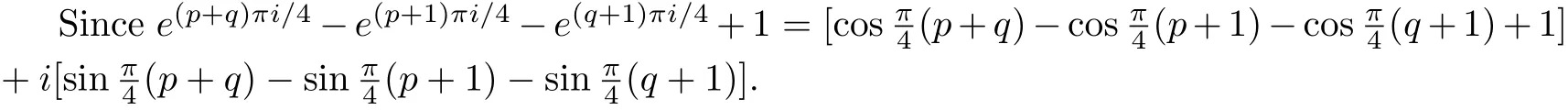
Its imaginary part

Its real part

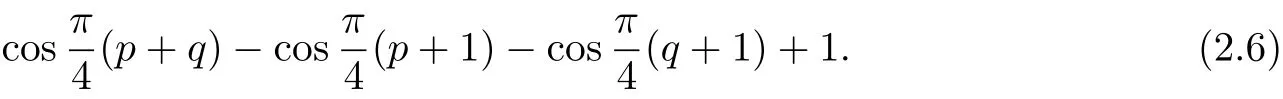
If its imaginary part is not zero,then the theorem is right;if its imaginary part is zero,we need to prove its real part is not zero,and then the theorem is right.

Since(p,q)=1,p and q is symmetrical,we need to divide into two cases to discuss.

(i)When p and q are all odd number,we may set

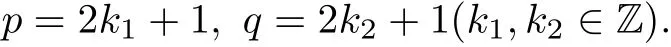
Then the formula(2.5)becomes as follows.

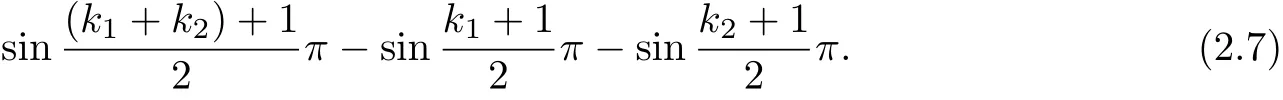
Since k1,k2∈Z and by the period of the Sine function,then

Iftheformula(2.7)equals0,thenthevaluationsofsinneed to satisfy the following table.

Table 1The Value of Sine Function

Therefore,eπi/4can not be the zeros of the Jones polynomials for torus knots Tp,q(when p and q are all odd number).

(ii)When one of p and q is an odd number and the other is an even number,we may set p=2k1+1,q=2k2(k1,k2∈Z)and then the formula(2.5)is the following formula.

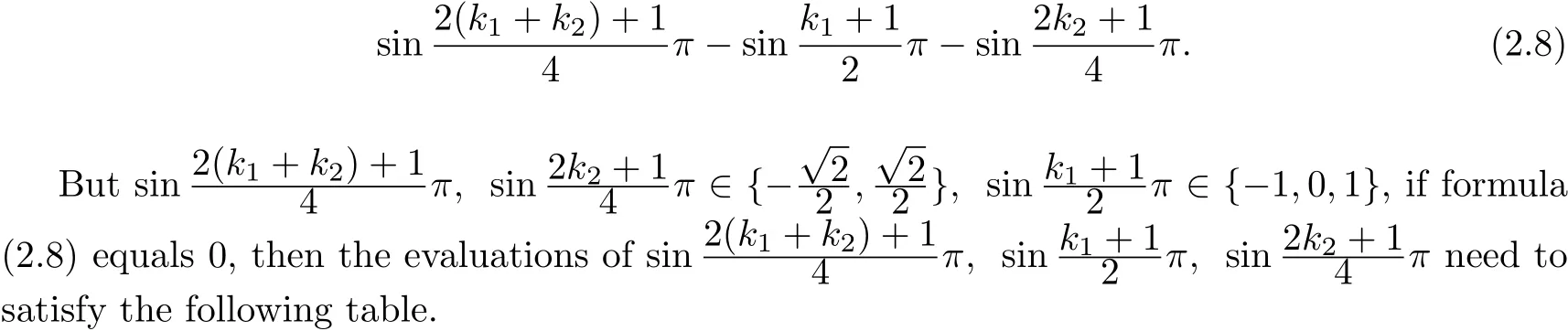
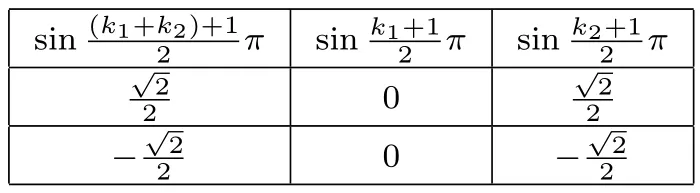
Table 2The Value of Since Function

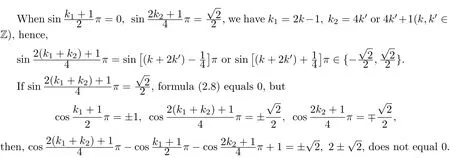
Therefore eπi/4can not be the zeros of the Jones polynomials for torus knots Tp,q(when one of p and q is an odd number,and the other is an even number).Similarly,one can prove the other cases.

In one word,eπi/4can not be the zeros of the Jones polynomials for torus knots Tp,q(for all p and q).

Similarly,e3πi/4,e5πi/4,e7πi/4can not be the zeros of the Jones polynomials for torus knots Tp,q(for all p and q).

Therefore,e(2m+1)πi/4(m is a positive integer)can not be the zeros of the Jones polynomials for torus knots Tp,q.

§3.The Zeros of Jones Polynomial for 2-bridge Knots

Let c1,c2,···,crbe a group of nonzero integer(may be positive or negative number),we shadow the knots diagram as following,the ciof this diagram is the crossing number at this position,denoted 2-bridge knots by C(c1,c2,···,cr).

Figure 22-bridge Knot r=2k

Making and simplifying it to the fraction(β≥0),there are the following facts.

Figure 32-bridge Knot r=2k+1

(1)When β is an odd number,it is a knot,otherwise it is a link with two components;

(2)C(−c1,−c2,···,−cr)is the mirror image of C(c1,c2,···,cr)(ci/=0,ci∈Z).

Lemma 3.1[4]The Jones polynomial of C(−2c1,2c2,···,(−1)r2cr)is written by the following recursive formula

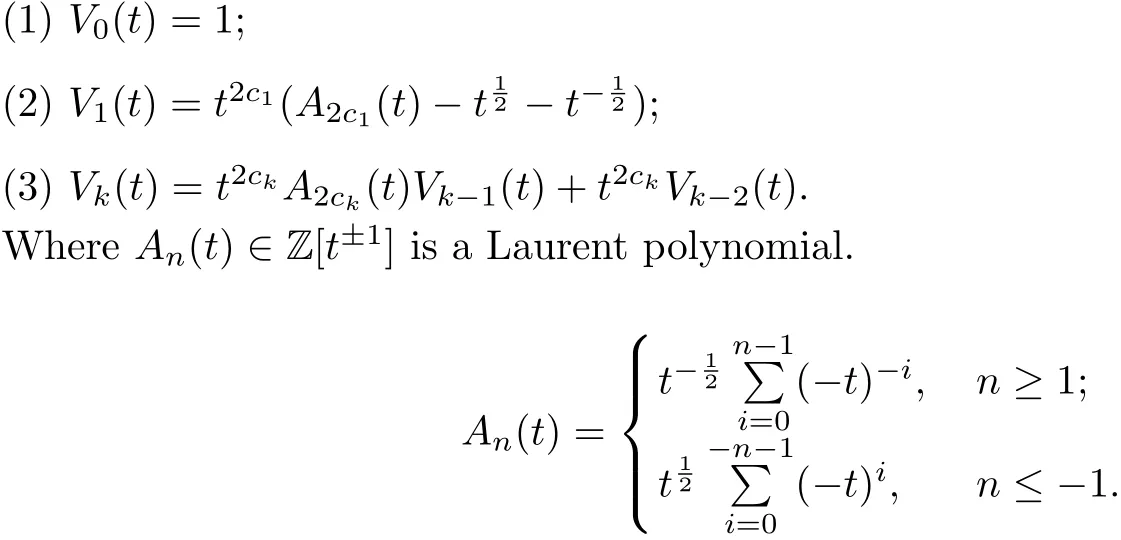
Specially,when c1=c2=···=cr=1,we study Jones polynomial for C(−2.2,···,(−1)r2).

Theorem 3.1The zeros of the Jones polynomial for 2-bridge knots C(−2.2,···,(−1)r2) are distributed on the unit circle when k→∞.

ProofThe f i rst step:calculating the Jones polynomial for C(−2.2,···,(−1)r2).

Setting V(t)+xV(t)=λV(t)+xV(t),compared with the formula mentionedkk−1k−1k−2

above,there is

Remove x,we have that λλ−p(t)=q(t),that is

Subtracting the two formulas,then

The second step:we prove that the zeros of the Jones polynomial for 2-bridge knots C(−2,2,···,(−1)r2)are distributed on the unity circle.

Setting the numerator of(3.3)equals 0,then

Corollary 3.1The zeros of the Jones polynomial for 2-bridge knots C(−2K,2K,···, (−1)r2K)(where K is a nonzero integer constant)are distributed on the curves|λ1/λ2|=1 when k→∞,where λ1and λ2are the roots of the equation λ2−t2KA2K(t)λ−t2K=0.

AcknowledgmentThe authors would like to thank the referees for kind suggestions and many useful comments.

[1]ALEXANDER J W.Topological invariants of knots and links[J].Trans Amer Math Soci,1928,30(2): 275-306.

[2]JONES V F R.Hecke algebra representations of braid groups and Lpolynomials[J].Annals of Math,198, 126:335-388.

[3]LOUIS H,KAUFFMAN.New invariants in the theory of knots[J].AMM,1988,95(3):195-242.

[4]EUNJU Lee,SAND Youl Lee,SEO Myoungsoo.A Recursive formula for the Jones polynomial of 2-bridge links and applications[J].J Korean Math Soc,2009,46(5):919-947.

[5]JIN Xian-an,ZHANG Fu-ji.Zeros of the Jones polynomials for families of pretzel links[J].Phys A,2003, 328(3-4):391-408.

[6]LANDVOY R A.The Jones polynomial of pretzel knots and links[J].Topology and its Applications,1998, 83:135-147.

[7]WU F,WANG J.Zeros of the Jones polynomials[J].Phys A,2001,296(3-4):483-494.

[8]TAO Zhi-xiong.On the roots of Jones polynomial[J].Chinese Annals of Mathematics,2013,32A(1):63-70.

[9]HAN You-fa,YAN Xi-ming,L¨U Li-li.The colored Jones function[J].Chinese Quarterly Journal of Mathematics,2012,27(1):87-91.

tion:57M15,57M25

1002–0462(2014)04–0612–08

date:2013-08-25

Supported by the National Science Foundation of China(11471151);Supported by Program for Liaoning Excellent Talents in University(LR2011031)

Biography:HAN You-fa(1962-),male,native of Changchun,Jilin,a professor of Liaoning Normal University, Ph.D.,engages in low-dimension topology.

CLC number:O189.3Document code:A