位移相关减振器对车辆悬架特性的仿真研究

董明明， 边 楠

(北京理工大学 机械与车辆学院， 北京 100081)

位移相关减振器对车辆悬架特性的仿真研究

董明明， 边 楠

(北京理工大学 机械与车辆学院， 北京 100081)

针对减振器在高频激励下存在的发热问题，提出了一种阻尼特性与位移相关的叶片式减振器，即在减振器静平衡位置设计附加通道，改变减振器的阻尼特性，以降低发热功率. 利用MATLAB/Simulink建立了二自由度悬架振动模型，在特定频率的路面激励下针对不同的附加通道尺寸对车身加速度、悬架动挠度及减振器发热功率进行了仿真分析. 结果表明：在车辆悬架上用阻尼特性与位移相关的减振器，可以有效地降低发热量.

减振器；阻尼特性；发热功率；MATLAB/Simulink

车辆减振器是悬架系统的主要组成部件之一，在车辆行驶过程中起着重要作用，其中，液压减振器应用广泛. 液压减振器的阻尼力是通过工作液体流经节流小孔、缝隙时产生节流效应而产生的，它能有效地衰减簧上、簧下质量的相对运动，提高车辆的行驶平顺性和操纵稳定性[1]. 车辆行驶时，路面不平度的激励引起减振器两端的相对运动，减振器衰减振动能量并将其转化为热能，由此导致减振器工作温度上升，使工作液体粘度发生改变，进而影响减振器的阻尼力，并最终影响车辆悬架系统的综合性能. 此外，减振器温度的升高还会加速其密封元件的老化，引起过早失效，也容易引起减振器工作液的空化效应，导致减振器特性畸变. 因此，在减振器的设计开发过程中,重视其热力学设计是十分重要的[2].

目前，国内外对液压减振器的研究主要集中在减振器阻尼作用的建模方法与仿真分析研究，并且在建模与仿真分析时，往往忽略温度对阻尼力的影响，对于热力学的研究还不够完善[3-5]. 张立军等人[6]建立了减振器热机耦合动力学模型并进行仿真分析，利用减振器发热特性试验数据辨识了减振器热动力学模型参数. 顾亮等人[7]对叶片式减振器的热稳定性做了详细的分析. 但以上的研究仅对减振器的发热做了理论分析，并没有提供一种有效的解决方案. 所以，有必要研制一种新型液压减振器，在不影响平顺性的前提下，有效降低发热量.

提出了一种新型液压减振器的结构形式，该结构形式物理可实现，在筒式液压减振器和叶片式液压减振器上均可以运用. 路面不平度的激励存在高频信号幅值小，低频信号幅值大的现象；液压减振器在受到高频信号时发热量大，受到低频信号时发热量小. 由此可见，在路面激励幅值小的时候降低减振器的阻尼可以有效降低其发热量. 结构方面，对于筒式减振器和叶片式减振器，在其静平衡位置一定长度范围内对其工作壁向外部进行冲压，增大其工作直径，使工作液从活塞或叶片与工作壁的缝隙流过，有效降低减振器的阻尼，从而降低发热量.

文中旨在分析这种新型结构的减振器发热量变化以及其对车辆平顺性的影响，对叶片式减振器进行理论研究和仿真分析. 首先，建立车辆悬架振动模型及其微分方程，构造减振器分段阻尼，对减振器的发热量及平顺性进行理论分析；然后，在MATLAB/Simulink中建立仿真模型，得出车身加速度、悬架动挠度以及发热功率的仿真结果；最后，对仿真结果进行分析，结合理论分析，得出结论.

1 叶片式减振器的结构和工作原理

叶片式减振器的工作原理如图 1所示. 叶片式减振器由壳体、隔板总成、叶片总成、拉臂(图中未画出)等组成，其中隔板总成与固定在车体上的壳体连接，为固定件；叶片总成与拉臂连接，拉臂通过连杆机构与车轮连接，为活动件. 隔板总成与叶片总成呈“十”字交叉装配在壳体内，壳体内充满工作液，车轮相对于车体运动时，拉臂带动叶片总成在壳体内转动，使叶片运动前方的工作液产生高压，通过叶片上的常通孔及叶片与壳体、隔板与壳体之间的缝隙等各个通道流向叶片背面. 减振器工作时叶片在壳体内旋转，工作腔内液体的总流量等于单位时间内叶片扫过的体积.

静平衡位置附加通道即在壳体内侧加工一个特定尺寸的凹槽，使得减振器在静平衡位置附近工作时产生较小的阻尼，以实现位移相关的阻尼特性.

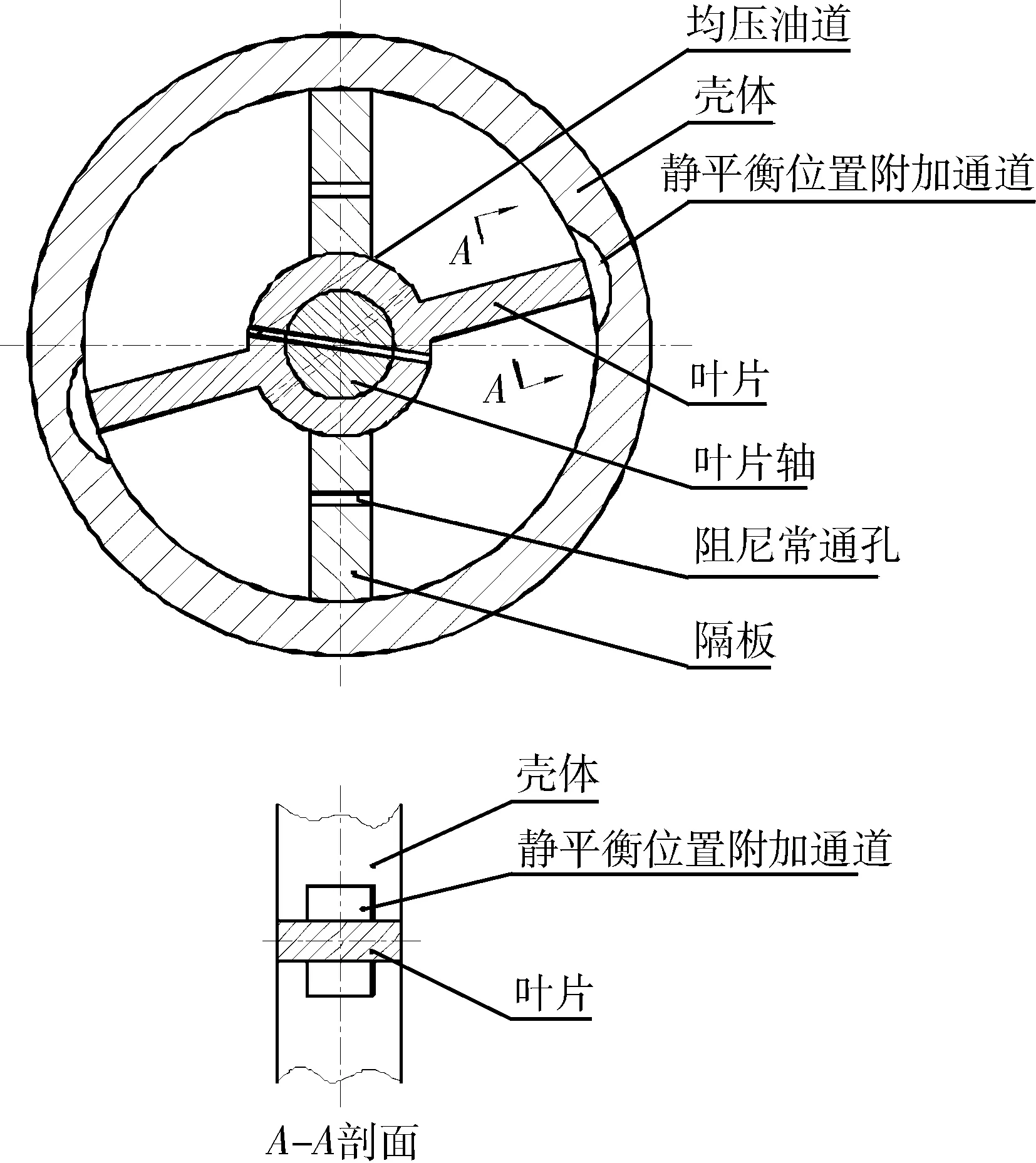
图1 叶片式减振器结构简图

2 理论分析

2.1 二自由度悬架振动模型的建立

讨论阻尼对车身振动的影响，考虑到计算精度将悬架简化成如图 2所示的二自由度振动系统.

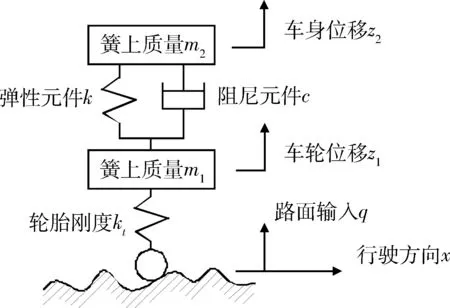
图2 二自由度振动模型

图中,m2为簧上质量，kg；m1为簧下质量，kg；k为悬架刚度，N/m；kt为轮胎刚度，N/m；c为减振器阻尼系数，Ns/m；z2为车身位移，m；z1为车轮位移，m；q为路面不平度位移，m.

建立该系统的微分方程如下

(1)

将式(1)化为如下形式

(2)

2.2 减振器的发热功率

减振器的发热是一个十分复杂的过程，为了便于分析，文中仅对减振器的工作液流经通孔时产生的热量进行分析，忽略工作液的流体特性.

减振器的发热功率可以衡量其发热量大小，表达式如下

(3)

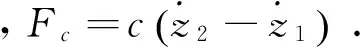
故式(3)可以写成

(4)

由式(4)可知，控制减振器阻尼系数c可以有效控制其发热功率. 文中研究的新型结构减振器，在其平衡位置附近阻尼系数很小，可视为零，并且我们假设减振器在其余位置的阻尼系数为一常数，则该减振器的阻尼系数表达式如下

(5)

式中：c0为阻尼系数常数；φ为减振器旋转角度，φ=0时为静平衡位置，φ0为变阻尼角度，该位置减振器的阻尼系数发生改变，对应减振器旋转角速度为ω0，对应的簧上质量与簧下质量之间的相对位移称为变阻尼位移，记为s.

阻尼特性曲线如图 3所示.

图 3 位移相关叶片式减振器阻尼特性曲线

2.3 悬架系统的平顺性

我们不仅分析了叶片式减振器的变阻尼角度对发热功率的影响，还分析了其对该系统的平顺性的影响.

悬架动挠度(Δzd)的表达式如下

(6)

3 仿真分析

3.1 仿真模型的建立

根据式(2)在MATLAB/Simulink中建立二自由度仿真模型，如图 4所示. 其中Subsystem模块为阻尼系数取值模块，Subsystem1模块为路面输入模块.

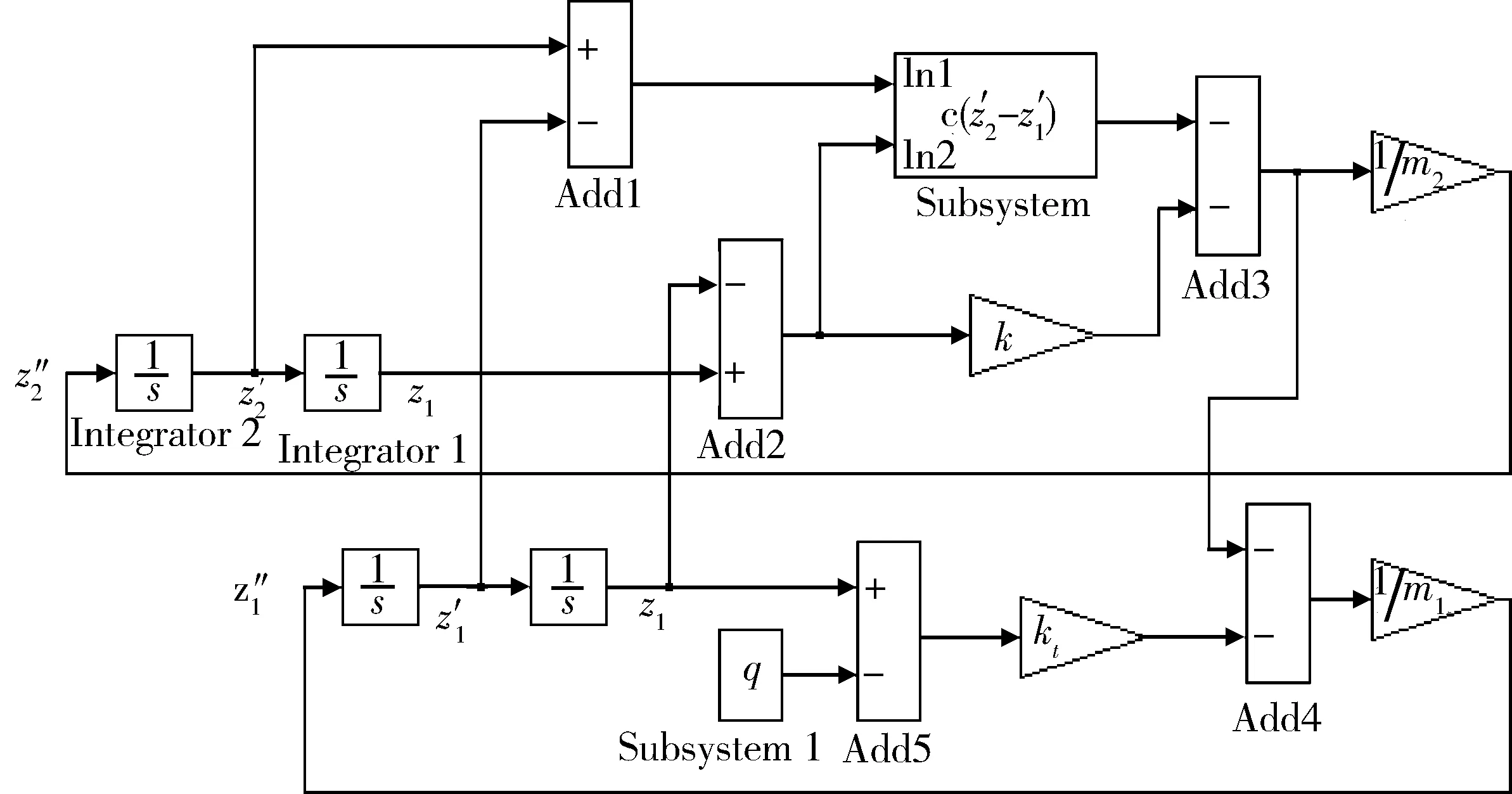
图 4 二自由度车辆振动Simulink模型

路面激励采用正弦波激励，表达式为

q=Asin(2πft).

(7)

仿真参数如表 1所示.

表1 仿真参数设置

二自由度振动模型参数如表2所示.

表2 二自由度振动模型参数

3.2 仿真结果

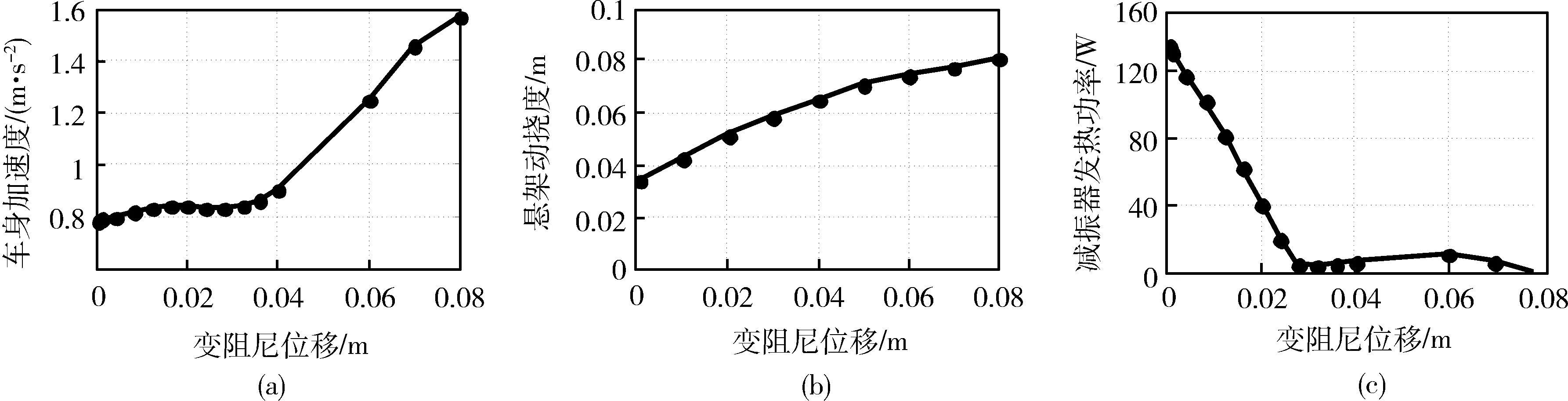
图5 0.6 Hz激励下变阻尼位移对车身加速度、悬架动挠度、减振器发热功率的影响

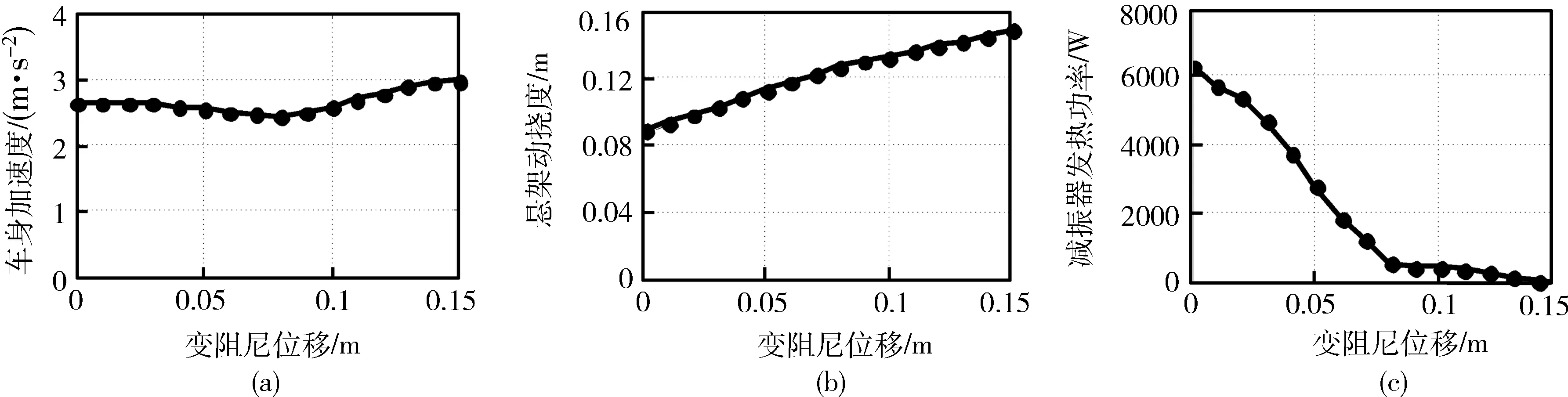
图6 1.4 Hz激励下变阻尼位移对车身加速度、悬架动挠度、减振器发热功率的影响

4 结 论

1) 建立的仿真模型正确，能体现该新型叶片式减振器的动力学特性，该模型在低、高频激励输入下具有相似的仿真特性，适用于各种频率段的激励输入；

2) 该新型减振器的变阻尼角度对悬架系统的车身加速度影响较小，满足设计要求；

3) 该新型减振器会增大悬架系统的动挠度，在确定结构尺寸时应保证悬架动挠度小于悬架设计动行程；

4) 该新型减振器可以有效降低发热功率，减少发热量，但在不同激励输入下的最佳变阻尼角度不同，设计时应根据路面输入来确定最优值.

[1] 余志生. 汽车理论[M]. 5版. 机械工业出版社, 2009.

[2] 张立军, 余卓平, 阳 鹏. 汽车液压减振器热机耦合特性试验研究[J]. 汽车技术, 2005(4): 1836.

[3] 董明明, 孟红芹. 油气弹簧刚度和阻尼特性及其影响因素仿真分析[J]. 车辆与动力技术, 2013(2): 47-50.

[4] 董明明, 顾 亮, 王国丽. 坦克叶片式减振器阻尼力的概率分析[J]. 兵工学报, 2004, 25(01): 1-4.

[5] 董明明, 黄 华, 顾 亮. 叶片式减振器的特性分析和液压参数识别[J]. 北京理工大学学报, 2004, 24(3): 206-209.

[6] 张立军, 余卓平. 汽车悬架液压减振器热机耦合动力学模型[J]. 同济大学学报(自然科学版), 2008,36(12): 1691-1696.

[7] Gu Liang, Qu Jinlin, Ding Faqian.Thermostability of Vane Absorber[J]. Journal of Beijing Institute of Technology (English Edition), 1998,7(02): 120-128.

Simulation on Suspension Characteristics of Absorber with Displacement-dependent Damping Property

DONG Ming-ming, BIAN Nan

(School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China)

In view of the heating problem in the absorbers under high-frequency vibration, a vane type absorber was proposed with a displacement-dependent damping property. At its static balance place of the absorber, an additional channel was designed for both changing its damping property and lowering the heating power. By means of MATLAB/Simulink, a 2 DOFs suspension model was built. Through changing the dimensions of the additional channel, the different values in the car-body acceleration, suspension dynamic deflection and the absorber’s heating power were obtained in the road excitation with specific frequencies. The results indicated that the absorber could effectively lower the heating power.

Absorber; Damping property; Heating power; MATLAB/Simulink

1009-4687(2014)04-0020-05

2013-11-22.网络出版时间：2014-07-02 09:49

边 楠(1987-)，男，硕士.

U463.33+4.4

A

URL: http://www.cnki.net/kcms/detail/11.4493.TH.20140702.0949.001.html